$\mathit{\text{ MATERIAL EN REVISIÓN}}$

Introducción

En la sección anterior hablamos sobre la métrica que se asigna entre dos puntos de un conjunto. Estamos tan acostumbrados a unir, automáticamente, dos puntos con el segmento que los une, que es natural que asumamos que la longitud de este segmento definirá la distancia entre ellos. No obstante, puede haber situaciones donde sea necesario considerar factores que nos hagan modificar la manera en que definimos esa distancia. Veamos algunos ejemplos.

Supongamos que nos encontramos en un poblado y nos interesa partir del punto $A$ para llegar al punto $B$ usando el camino más corto. No nos es posible caminar sobre la recta que, en la geometría euclideana une a los dos puntos, pues esto implicaría tener que atravesar las casas y las construcciones que se ubiquen sobre ella. En estas circunstancias lo que resta es desplazarse sobre las calles, en la manera en que lo haría un taxista (suponiendo que no hay restricciones adicionales al recorrido, como el tráfico o el sentido de la vialidad).

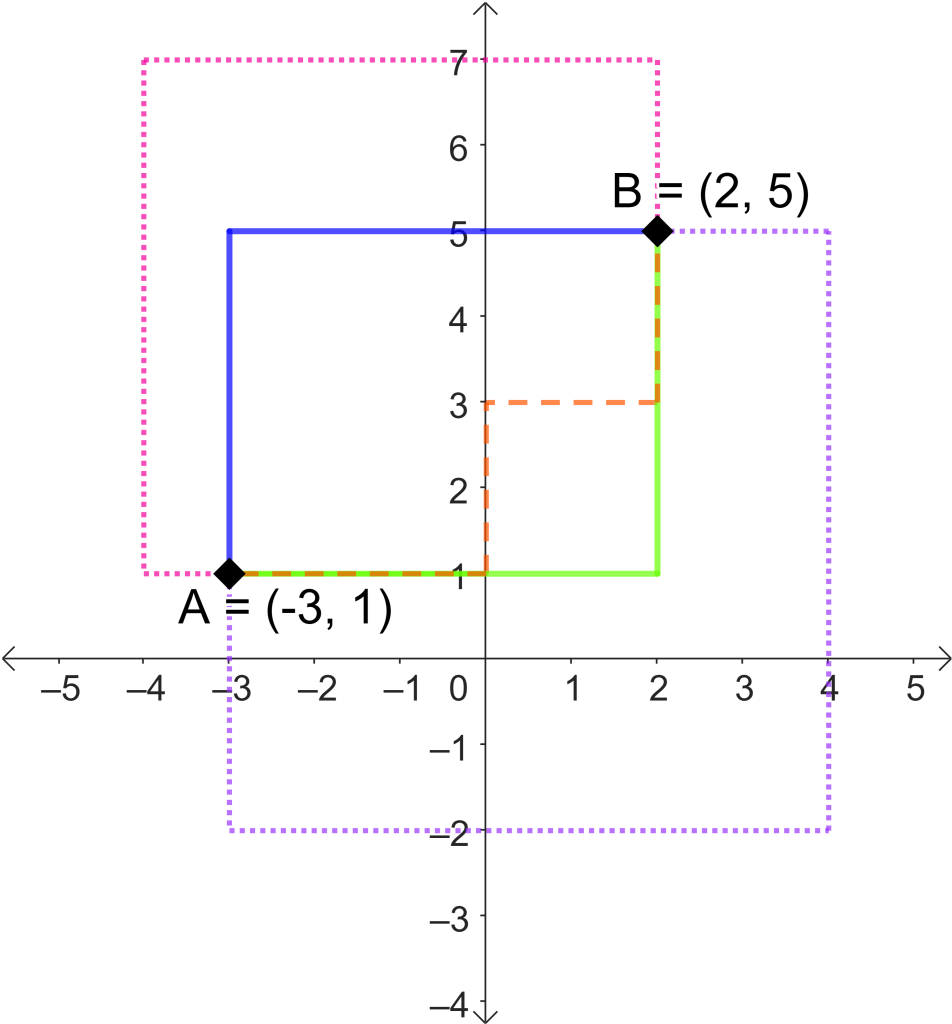
En la imagen se pueden visualizar algunas posibles rutas.

Si definimos la distancia como el menor número de cuadras que separan al punto $A$ del punto $B$, podemos observar que los caminos verde, azul y naranja representan rutas de distancia mínima. Cada una de estas cuadras se puede proyectar de manera horizontal y vertical sobre la recta horizontal que tiene a $A$ y la recta vertical que tiene a $B$. En consecuencia, definimos la métrica para dos puntos $A=(a_1,a_2)$ y $B=(b_1,b_2)$ en el conjunto ${\mathbb{R}}^2$ como:

$$d(A,B)=|b_1-a_1|+|b_2-a_2|$$

Métrica del ascensor

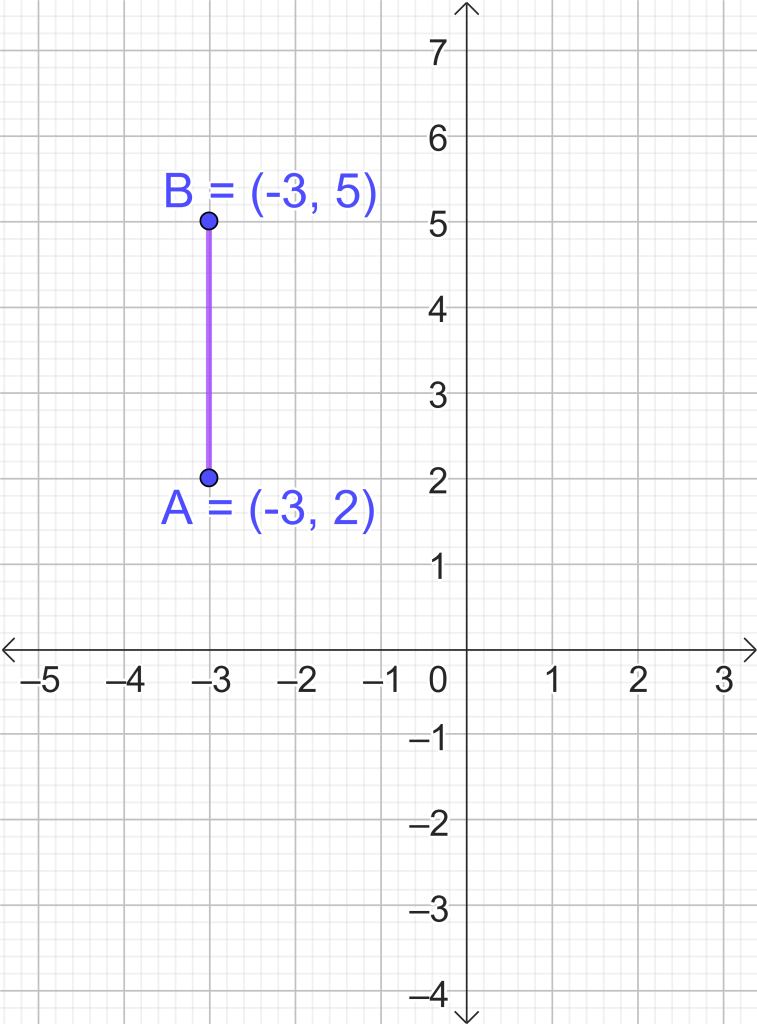
Ahora nos encontramos en cierta planta de un edificio y nos interesa movernos a otra planta. Si el punto al que vamos se encuentra en el mismo edificio, simplemente nos dirigimos al ascensor, en la misma planta, hasta recorrer la cantidad de pisos deseados. Esta situación se representa en la siguiente imagen:

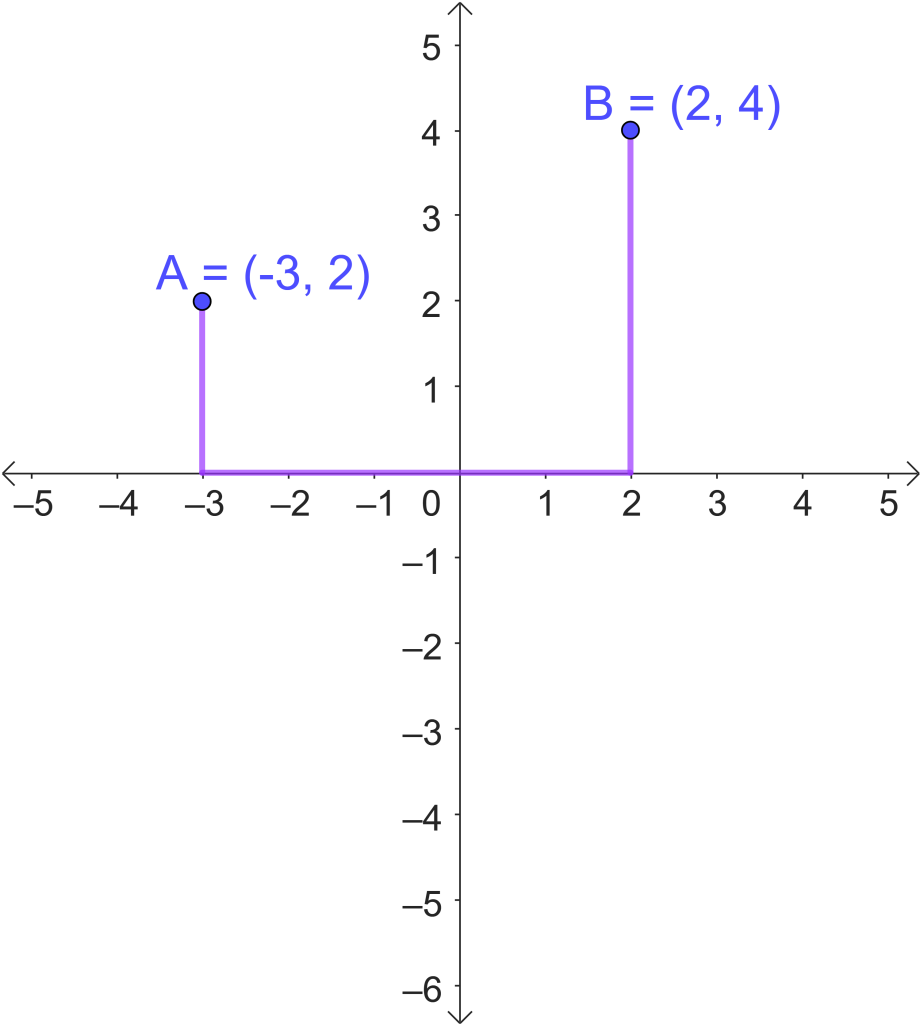
Por otra parte, si nos interesa llegar a un piso de otro edificio que está sobre la misma calle, debemos tomar el ascensor del edificio en que nos ubicamos hasta llegar a la planta baja, caminar hasta el otro edificio y, posteriormente, tomar el ascensor ahí hasta llegar a nuestro destino. Este movimiento puede visualizarse a continuación:

A partir de esto se define la métrica para dos puntos $A=(a_1,a_2)$ y $B=(b_1,b_2)$ en el conjunto ${\mathbb{R}}^2$ como:

$$d(A,B)=\{\begin{array}{lcc}|b_2-a_2|& si& a_1=b_1\\ \\ |a_2|+|b_1-a_1|+|b_2|& si& a_1\ne b_1\end{array}$$

Métrica de Hamming

En el ámbito de la Teoría de la Información interesa contar el número de cambios que se requieren para que una palabra se convierta en otra. Por ejemplo:

Para convertir «casa» en «pasa» se requiere cambiar una letra.
Para convertir «casa» en «taza» se requiere el cambio en dos letras.
Para convertir «roca» en «flor» se requiere cambiar cuatro letras.

Este número de cambios define la distancia de Hamming.

Para conocer más al respecto puedes consultar el libro:

Metcalf, L., Casey, W., Cybersecurity and Applied Mathematics. USA: Editorial ELSEVIER, 2016, págs 16 y 17.

El tablero de ajedrez

Consideremos las piezas Rey, Reina, Alfil, Caballo y Torre en el juego de ajedrez. De acuerdo a las reglas, cada una de estas piezas tiene un movimiento particular definido. Una pieza ubicada en la casilla $A$ requiere una mínima cantidad de movimientos para llegar a la casilla $B.$ Demuestra que cada pieza define una métrica en el conjunto de puntos dado por las casillas del tablero de ajedrez.

Más adelante…

Recordaremos el concepto de espacio normado. Probablemente ya lo has visto en cursos de cálculo o álgebra lineal. Estos espacios inducen también una métrica entre sus puntos. ¿Será que todos los espacios métricos son inducidos por una norma?

Tarea moral

1. Demuestra que cada uno de los ejemplos anteriores es una métrica.
2. Define la métrica del taxista para puntos en ${\mathbb{R}}^n$.
3. Define la métrica del ascensor para edificios que no necesariamente estén sobre la misma calle. Combina con la métrica del taxista.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.