(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta nota hablaremos de lo que es una relación entre dos conjuntos $A$ y $B$, utilizaremos ese concepto para poder definir lo que significa una función entre dos conjuntos $A$ y $B$, que será una relación en la que cada elemento de $A$ se relaciona con uno y sólo uno de $B$.
Definición
Sean $A$ y $B$ conjuntos, una relación de $A$ con $B$ es un subconjunto de $A\times B$, es decir un conjunto $\mathcal R$ tal que $\mathcal R\subseteq A\times B$.
El dominio de $\mathcal R$ es:
$Dom \mathcal R =\set{a\in A\mid \exists b\in B\,\,tal \,\,que \,\, (a,b)\in \mathcal R}$
La imagen de $\mathcal R$ es:
$Im \mathcal R =\set{b\in B\mid \exists a\in A\,\,tal \,\,que \,\, (a,b)\in \mathcal R}$
El codominio de $\mathcal R$ es el conjunto $B$. Si $(a,b)\in R$ diremos que $a$ está relacionado con $b$ y en ocasiones también se denota por $aRb$.
Ejemplos
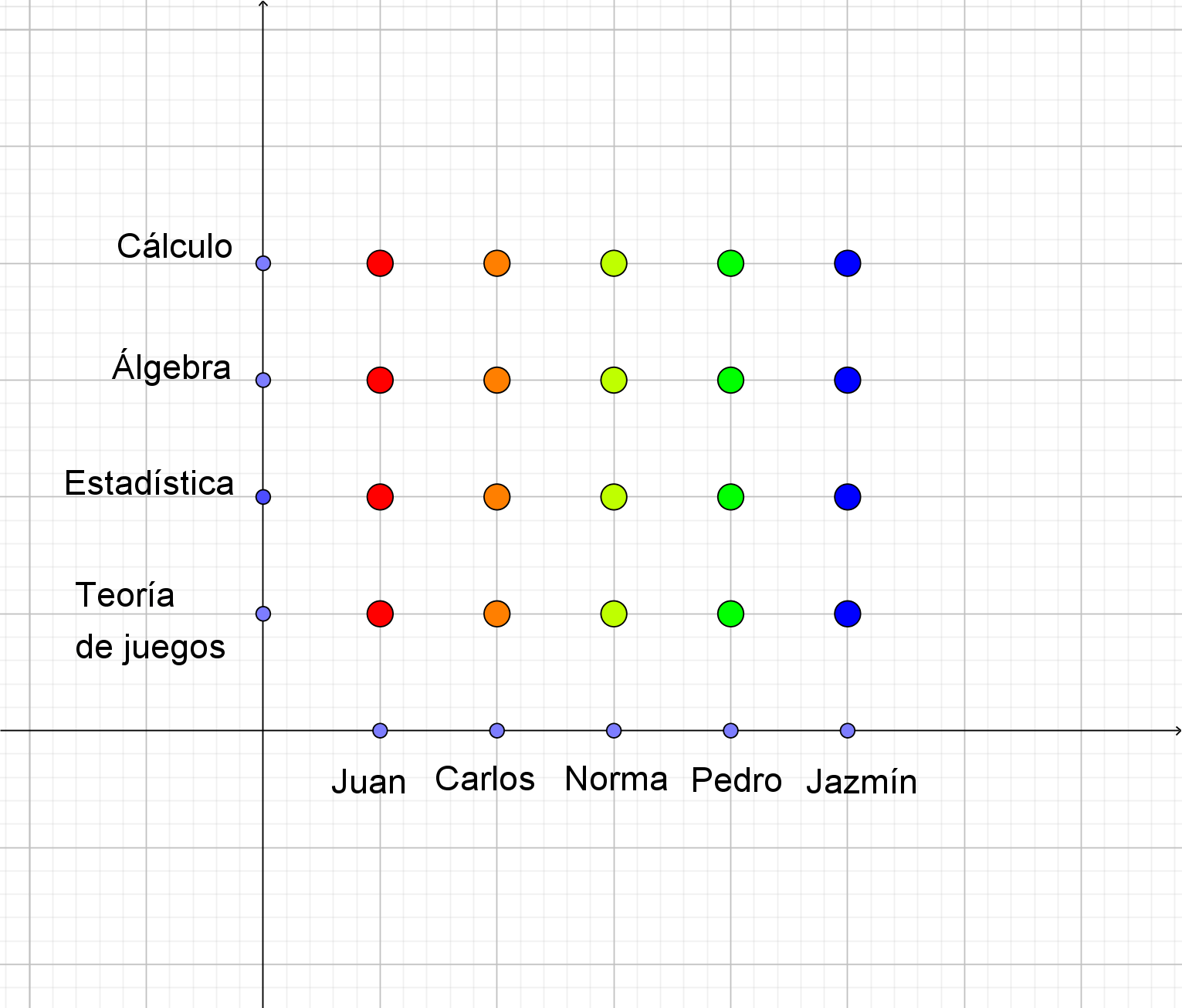
1. Sean $A=\set{Juan,Carlos,Norma,Pedro, Jazmín}$ y
$B=\set{ teoría\,\,de \,\, juegos, estadística, álgebra, cálculo}.$
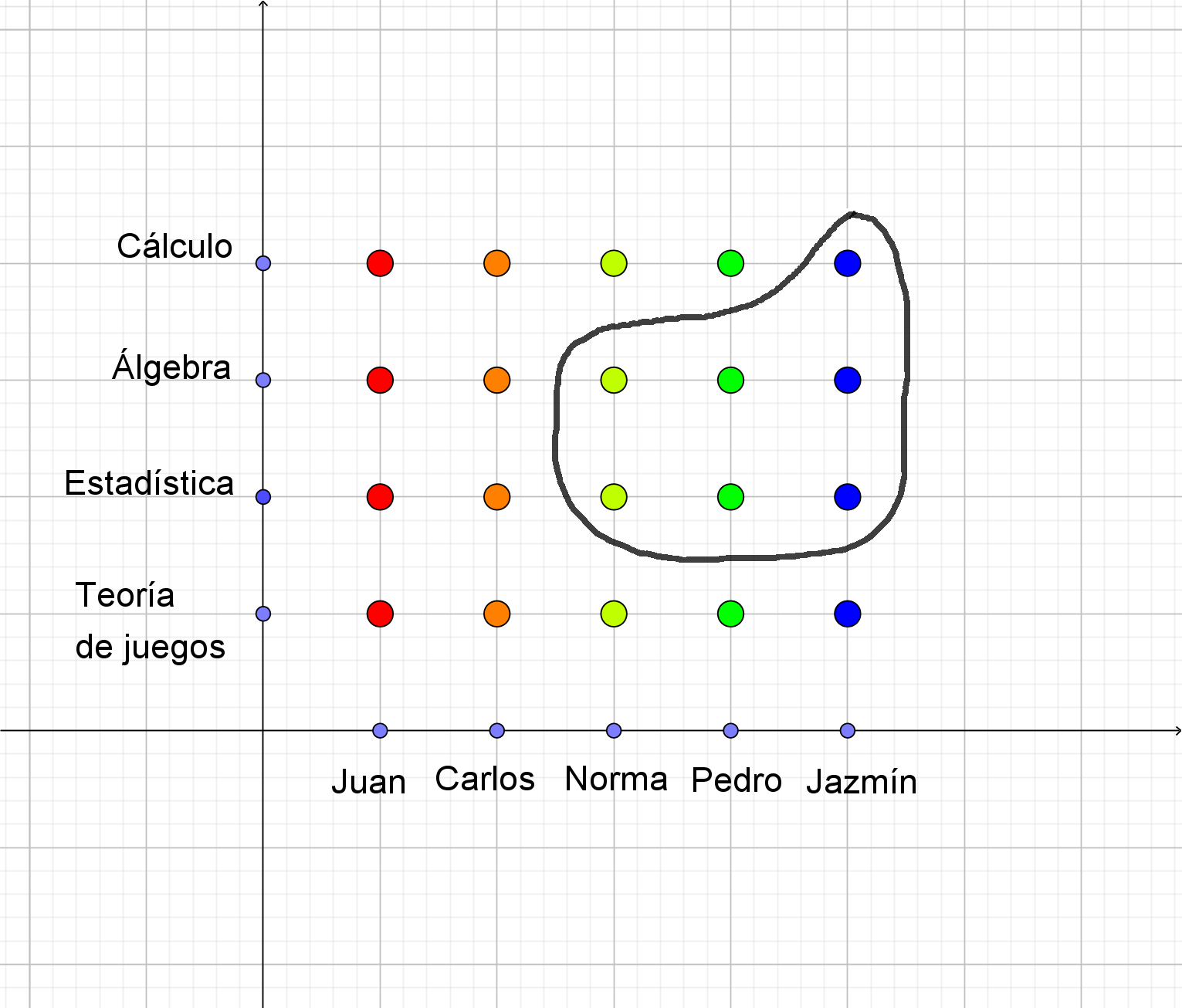
Entonces $\begin{array}{ll}\mathcal R&=\{(Norma, estadística),(Norma, álgebra), (Pedro, estadística),\\&(Pedro, álgebra), (Jazmín, estadística),(Jazmín, álgebra),(Jazmín, cálculo)\}\end{array}$
es una relación de $A$ con $B$.
$Dom \mathcal R =\set{Norma, Pedro, Jazmín}$
$Im \mathcal R =\set{estadística, álgebra, cálculo}$
A continuación se muestra el producto cartesiano de ambos conjuntos.
Cualquier subconjunto del producto cartesiano será una relación de los dos conjuntos. Por ejemplo consideremos los siguientes subconjuntos:
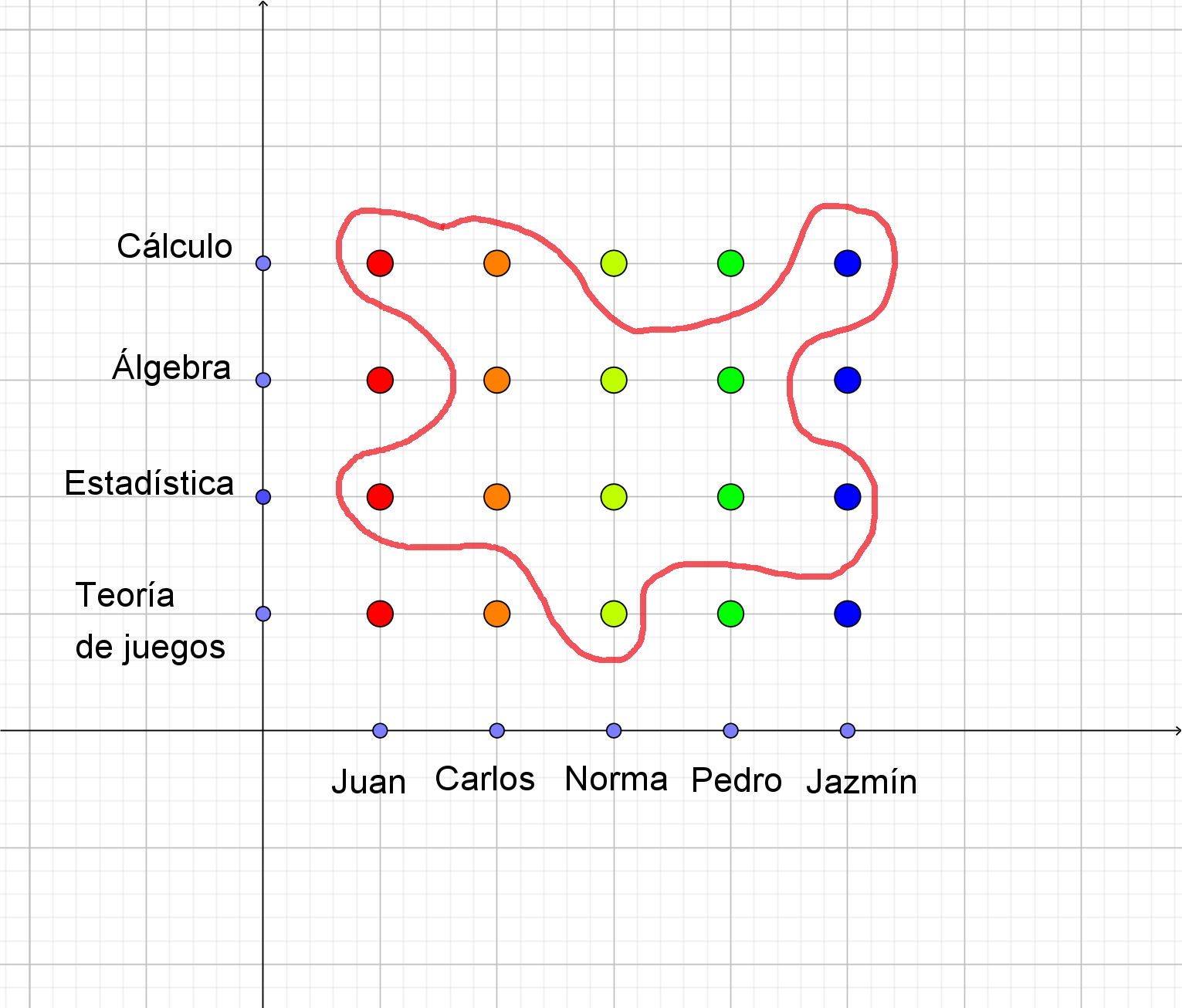

Dejamos como ejercicio al lector que escriba las relaciones anteriores mediante un conjunto de parejas ordenadas.
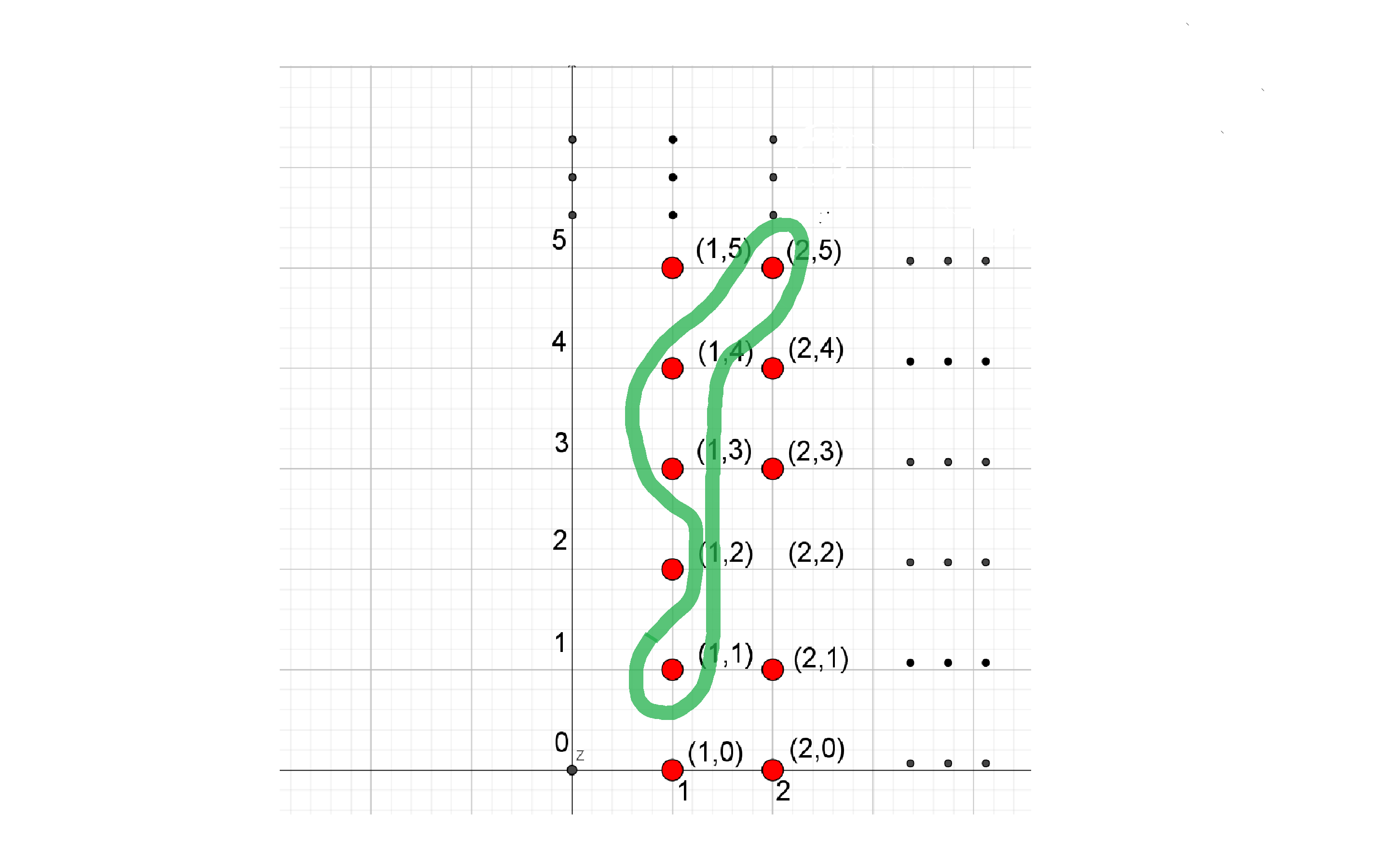
5. $\mathcal R\subseteq \mathbb N\times \mathbb N$
$\mathcal R=\set{(1,1),(1,3),(1,4),(2,5)}$
$Dom \mathcal R =\set{1,2}$
$Im \mathcal R =\set{1,3,4,5}$
6. $\mathcal R\subseteq \mathbb R\times \mathbb R$
$\mathcal R=\set{(x,y)\in\mathbb R\times \mathbb R \mid \left|x \right|=\left|y \right|}$.
Observa que:
$(1,-1)\in \mathcal R$ ya que $\left|1 \right|=\left|-1\right|,$
$(1,1)\in \mathcal R$ ya que $\left|1 \right|=\left|1\right|,$
$(-\pi,\pi)\in \mathcal R$ ya que $\left|-\pi \right|=\left|\pi \right|,$
$(1,5)\notin \mathcal R$ ya que $\left|1 \right|=\left|5 \right|,$
$(3,-7)\notin \mathcal R$ ya que $\left|3 \right|=\left|-7\right|.$
De manera más general observamos que todos los puntos de las rectas $y=-x$ y $y=x$ están en la relación. Mueve los puntos por las rectas en el siguiente recurso de geogebra y constátalo.
7. $\mathcal R\subseteq \mathbb Z\times \mathbb Z$
$\mathcal R=\set{(a,b)\in\mathbb Z\times \mathbb Z \mid\,\,a\,\,y\,\,b\,\,tienen\,\,la\,\,misma\,\,paridad}$.
$(5,-1)\in \mathcal R$, $(2,6)\in \mathcal R$, $(0,-4)\in \mathcal R$, $(3,8)\notin \mathcal R$.
Observa que la relación se puede describir como $\mathcal R=\set{(k,-k+2n)\in \mathbb Z\times \mathbb Z \mid k\in \mathbb Z,n\in \mathbb Z}$. En el siguiente clip se muestra gráficamente la disposición de algunas de estas parejas ordenadas.
En el siguiente recurso de geogebra mueve el valor de los deslizadores $n$ y de $k$ para obtener los puntos en el plano con la misma paridad.
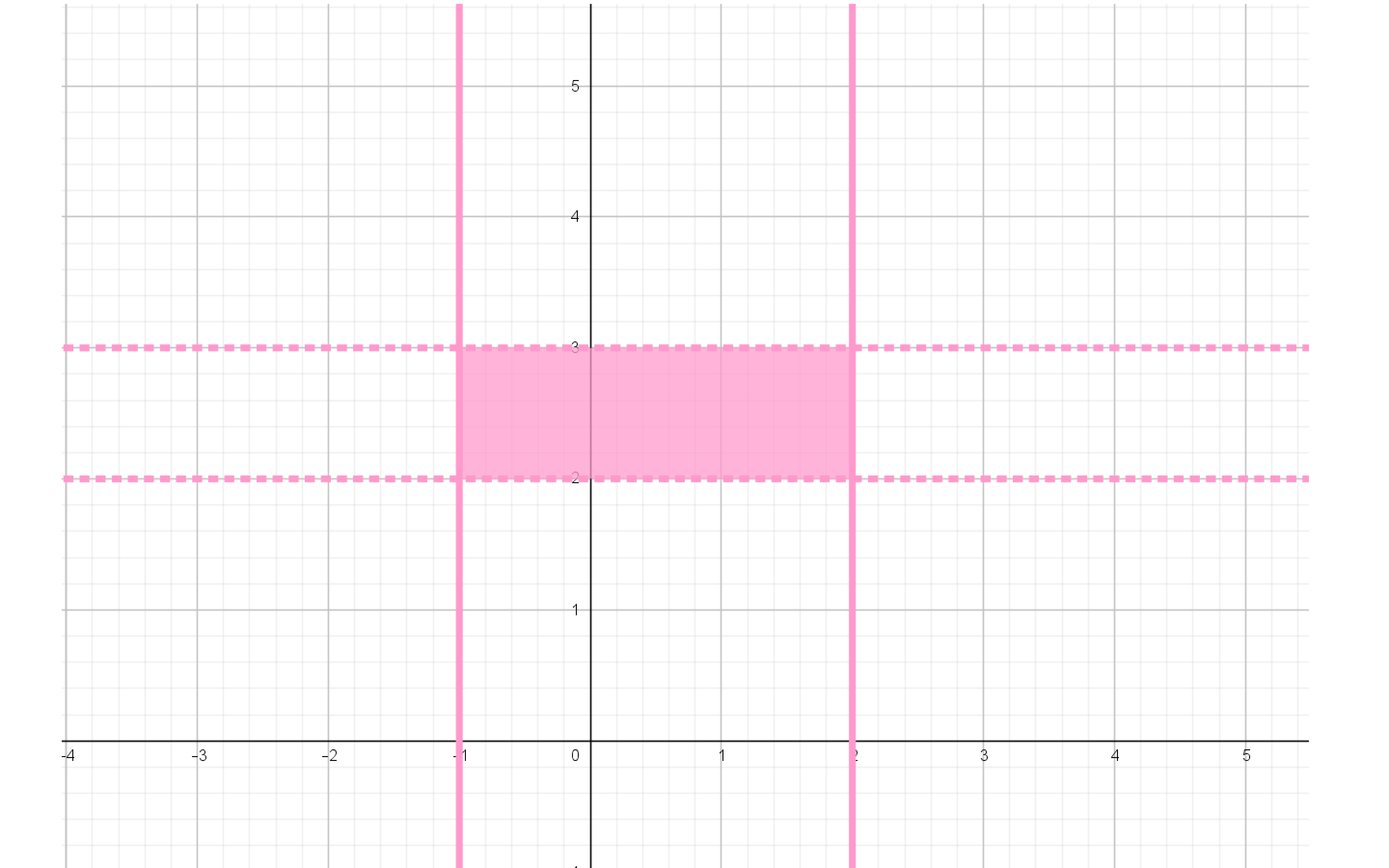
8. $\mathcal R=[-1,2]\times (2,3)\subseteq \mathbb R^2$
$\mathcal R=\set{(x,y)|-1\leq x\leq 2,2<y<3}$
$Dom \mathcal R =[-1,2]$
$Im \mathcal R =(2,3)$
La siguiente imagen nos muestra gráficamente la relación:
Notemos que los conjuntos $A$ y $B$ no necesariamente son iguales y su elementos no siempre son números:
9. $\mathcal R\subseteq\mathbb R^2\times \set{\mathcal l\mid\mathcal l\,\,es\,\,una\,\,línea\,\,en\,\,el\,\,plano}$, $(p,\mathcal l)\in \mathcal R$ si y sólo si $p\in \mathcal l$.
$Dom \mathcal R =\mathbb R^2$
$Im \mathcal R$ son todas las líneas del plano.
Definición
Sean $A$ y $B$ conjuntos y $f$ una relación de $A$ con $B$. Decimos que $f$ es una función de $A$ en $B$ si:
- $Dom\, f=A.$
- Cada elemento $x\in A$ está relacionado con un solo elemento de $B$.
Es decir para todo $x\in A$ existe un único $y\in B$ tal que $(x,y)\in f$, a $y$ se le llama el valor de $f$ en $x$, o $f$ evaluada en $x$.
Notación: $f: A\to B$, $y=f(x)$ es el valor de $f$ en $x$, para indicar que la función $f$ le asigna a $x$ el valor $f(x)$ en ocasiones se escribe $ x\longmapsto f(x)$, para indicar la regla de correspondencia de $x$ un elemento del domino de la función $f$ a su correspondiente $f(x)$ en el codominio de la función.
Observa que la imagen de $f$ es:
$Im\, f =\set{y\in B\mid \,\, (x,y)\in f\,\,para \,\, alguna \,\, x\in A}$
=$ \set{y\in B\mid\,\,y=f(x)\,\,para \,\, alguna \,\, x\in A}$
=$\set{f(x)\mid x\in A}$
Ejemplos
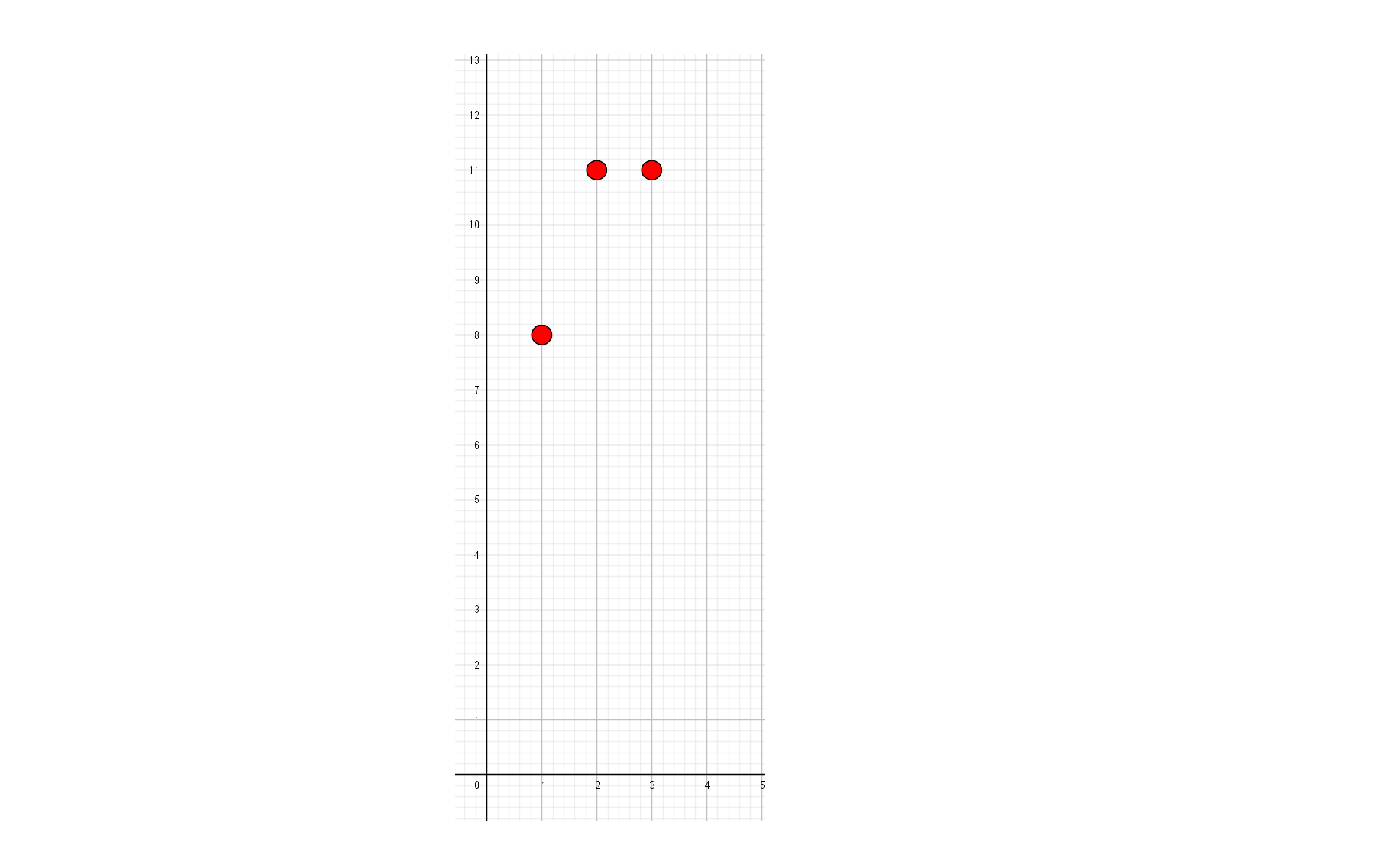
1. $A=\set{1,2,3}$, $B=\set{8,9,10,11}$,
$f:\set{1,2,3}\to \set{8,9,10,11}$ con $f=\set{(1,8),(2,11),(3,11)}$, es decir
$f(1)=8$, $f(2)=f(3)=11$. $Dom\,f=\set{1,2,3}$, $Im\,f=\set{8,11}$ , $B$ es el codominio de $f$
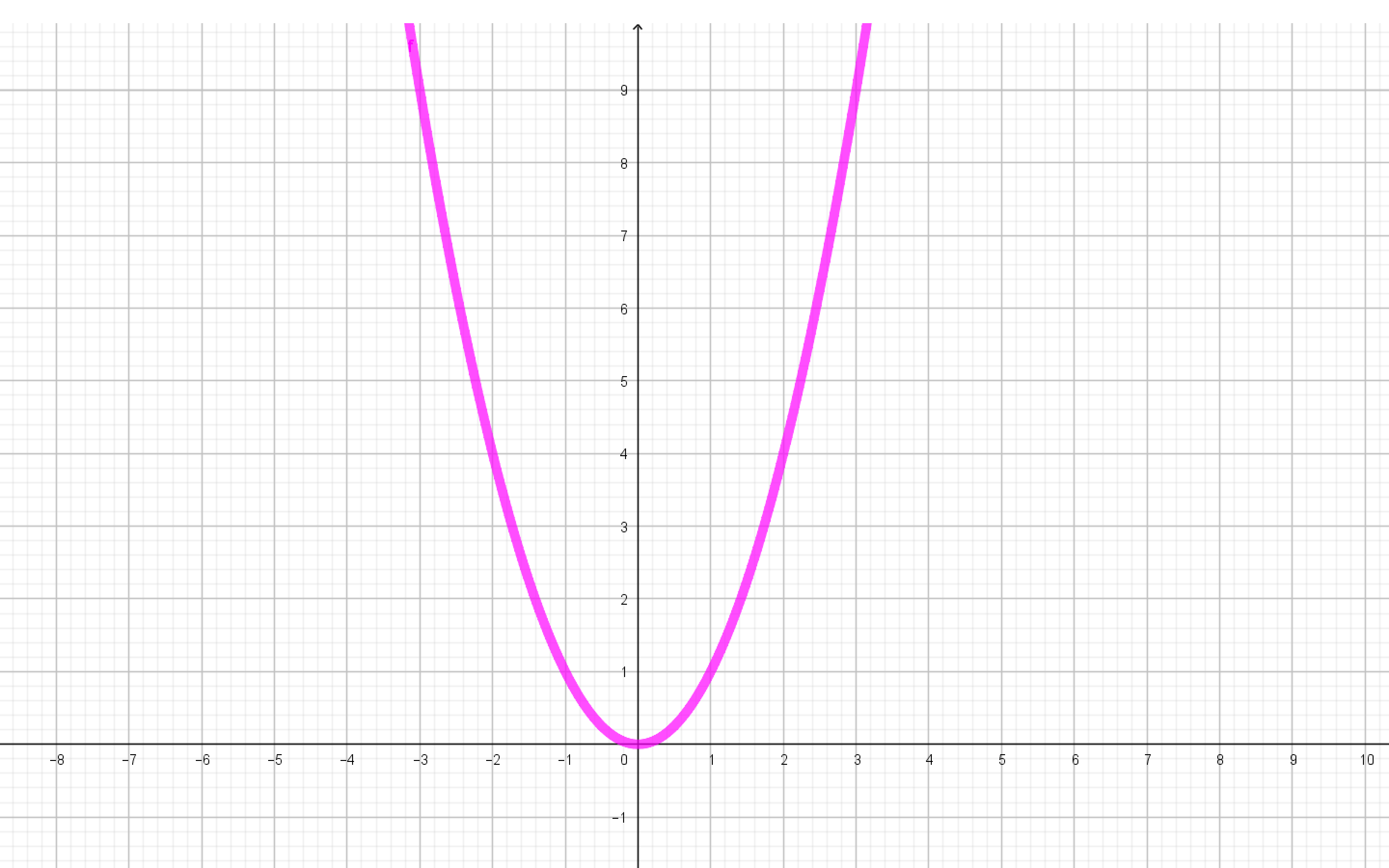
2. $g:\mathbb R\to \mathbb R$
$(x,y)\in g$ si y sólo si $y=x^2$
En este caso $g(x)=x^2.$
$Dom\,g=\mathbb R$, $\mathbb R$ es el codominio de $g$, mientras que $Im\,g=\set{g(x)\mid x\in \mathbb R}=\set{x^2\mid x\in \mathbb R }= \mathbb R^+\cup \set{0}$
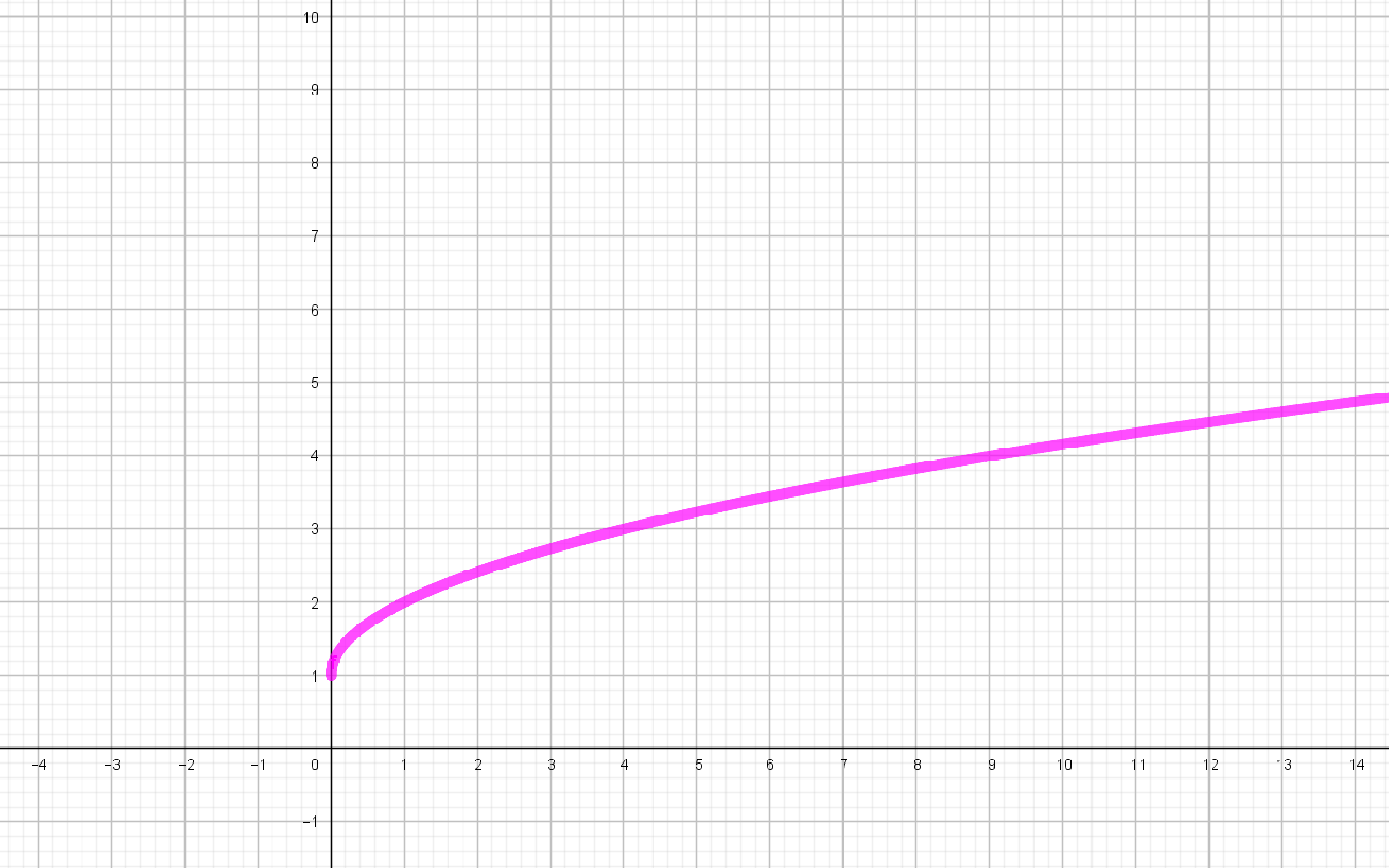
3. $h: \mathbb R^+\cup \set{0}\to \mathbb R$
$x\longmapsto +\sqrt{x} +1$
$h(0)=+\sqrt{0}+1=1$, $h(4)=+\sqrt{4}+1=2+1=3$
$Dom\,h= : \mathbb R^+\cup \set{0}$
$\mathbb R$ es el codominio de $h$.
$Im\,h=\set{h(x)\mid x\in \mathbb R^+\cup \set{0}}=\set{y\in \mathbb R\mid y\geq 1}= [1,\infty]$
Notación
Si $f:A\to B$ y $A$ es un conjunto finito $A=\set{a_1,\dotsi ,a_n}$, con $n$ elementos, podemos describir la regla de correspondencia de $f$ como :
\begin{pmatrix}a_1 & \dotsi & a_n\\
f(a_1) & \dotsi & f(a_n)\end{pmatrix}
Para terminar esta entrada debemos mencionar que, aunque las funciones son relaciones entre conjuntos, y, por lo tanto, conjuntos de parejas ordenadas, son un caso particular de relaciones muy importante y dado que en Álgebra será esencial no sólo la regla de correspondencia de una función sino su dominio y su codominio, la igualdad de dos funciones no se establecerá como la igualdad de los conjuntos de parejas ordenadas que las conforman sino que se establecerá una definición diferente. Cabe mencionar que sólo definiremos la igualdad de dos funciones cuando tengan el mismo dominio y el mismo codominio y en este caso estableceremos que son iguales cuando además coincida su regla de correspondencia:
Definición
Sean $A$ y $B$ conjuntos, dos funciones $f: A\to B$ y $g: A\to B$ son iguales ,$f=g$, si $f(x)=g(x)$ para toda $x\in A$ (es decir, si tienen la misma regla de correspondencia).
Tarea Moral
Determina el dominio, el codominio y la imagen de las siguientes relaciones $\mathcal R$ de $A$ con $B$ y determina si las relaciones son funciones de $A$ en $B$.
- $A=\set{2,8,5,6}$, $B=\set{-4,9,1,7,2}$
$\mathcal R=\set{(2,-4),(2,1,(5,9),(6,-4)}$ - $A=B=\mathbb R$, $(a,b)\in \mathcal R$ si y sólo si $a=|b|$
- $A=B=\mathbb R$, $(a,b)\in \mathcal R$ si y sólo si $|a|=b$
Sean $A=B=\set{x\in \mathbb R\mid -1\leq x\leq 1}$ y considera el subconjunto de $A\times B$, $C=\set{(x,y)\in \mathbb R\times \mathbb R\mid x^2+y^2=1}$.
¿Es $C$ una función de $A$ en $B$?
Más Adelante
En la siguiente nota seguiremos usando el concepto de función y estableceremos dos definiciones importantes, la de la imagen directa y la de imagen inversa y deduciremos algunas propiedades básicas pero muy importantes.
Enlaces relacionados
- Enlace a la nota anterior. Nota 6 Conjunto Potencia y el producto cartesiano.
- Enlace a la nota siguiente. Nota 8 Imagen directa e inversa de una función.
