(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Las matemáticas nos ofrecen herramientas sorprendentes para explorar combinaciones y posibilidades, en esta sección daremos la definición del conjunto potencia y del producto cartesiano. En el primero formaremos un conjunto cuyos elementos sean los subconjuntos de un conjunto dado, en el segundo consideraremos parejas formadas con los elementos de dos conjuntos cualesquiera.

Definición

Sea $A$ un conjunto, la potencia de $A$ es la colección de todos los subconjuntos de $A$ y la denotaremos por $\mathcal{P}(A)$, es decir

$\mathcal{P}(A)=\set{S\mid S\subseteq A}.$

Aunque $\mathcal{P}(A)$ es una colección que tiene en general más elementos que $A$, no habrá problema en considerarlo también como un conjunto y lo establecemos así en el siguiente axioma:

Axioma del conjunto potencia

Dado un conjunto $A$, $\mathcal{P}(A)$ también es un conjunto.

Ejemplos

• $A=\set{a,b}$
  $\mathcal{P}(A)=\set{\emptyset,\set{a},\set{b},\set{a,b}}$
• $B=\set{a,\set{b},\set{a,b}}$
  $\mathcal{P}(B)=\set{\emptyset,\set{a},\set{\set{b}},\set{\set{a,b}},\set{a,\set{b}},\set{a,\set{a,b}}, \set{\set{b},\set{a,b}},B}$

Observa que:

Para cualquier conjunto $\emptyset \in \mathcal{P}(A)$ y $A\in \mathcal{P}(A)$.

Definición

Sea $X$ el conjunto universo, $a,b\in X$.

El par ordenado de los objetos $a$ y $b$ es:

$(a,b)=\set{\set{a}, \set{a,b}}$

Observa que:

1. $(b,a)=\set{\set{b}, \set{b,a}}$
2. $(a,a)=\set{\set{a}, \set{a,a}}=\set{\set{a}, \set{a}}=\set{\set{a}}$

Proposición

Sea $X$ el conjunto universo, $a,b,c,d\in X$. Tenemos que

$(a,b)=(c,d) \Longleftrightarrow a=c\, \, \,y \, \, \, b=d$

Demostración

$\Longrightarrow $ Demostración de la implicación de ida

Supongamos que $(a,b)=(c,d)$, con la intención de mostrar que $a=c\, \, \,y \, \, \, b=d$.

Como $(a,b)=(c,d)$ entonces por definición de par ordenado:

$\set{\set{a}, \set{a,b}}=\set{\set{c}, \set{c,d}}$

La demostración se hace por casos.

Caso 1

Si $\set{a}= \set{c}$ y $\set{a,b}= \set{c,d}$ entonces $a=c$ de lo que se sigue, dado que $\set{a,b}= \set{a,d}$, que $b=d$, fíjate que demostramos que $a=c$ y $b=d$, que es lo que queríamos.

Caso 2

Si $\set{a}= \set{c,d}$ y $\set{a,b}= \set{c}$, entonces $a=c=d$ y $a=b=c$, así $a=b=c=d$, en particular $a=c$ y $b=d$

$\Longleftarrow $ Demostración de la implicación de regreso

Supongamos que $a=c$ y que $b=d$, por demostrar que $(a,b)=(c,d)$.

Por definición de par ordenado:

$(a,b)=\set{\set{a}, \set{a,b}}$

$(c,d)=\set{\set{c}, \set{c,d}}$

si $a=c$ y que $b=d$ entonces $\{a\}=\{c\}$ y $\{a,b\}=\{c,d\}$, por lo tanto $(a,b)=\set{\set{a}, \set{a,b}}= \set{\set{c}, \set{c,a}}=(c,d)$, que es lo que queríamos demostrar.

Como se cumplen las dos implicaciones la prueba está completa.

$\square$

Generalizando:

La terna $(a,b,c)$, es por definición el par $((a,b),c)$. En general si $(a_1,…,a_n)$ está definido, se define $(a_1,…a_{n+1})$ como: $( (a_1,…,a_n),a_{n+1})$. Notemos que tanto la terna como la n-ada son un par ordenado. Usando la proposición anterior y la definición de n-ada se puede probar que:

$(a_1,…,a_n)=(b_1,…,b_n)$ $ \Longleftrightarrow $ $a_i=b_i$, $\forall i$, $1\leq i\leq n$.

Definición

Sean $A$, $B$ conjuntos. El producto cartesiano de $A$ con $B$ es:

$A\times B=\set{(a,b)\mid a\in A,b\in B}$

Ejemplos

• $A=\set{\pi,2}, B=\set{3,4,5}$
  $A\times B=\set{(\pi,3), (\pi,4), (\pi,5),(2,3),(2,4),(2,5)}$
  $B\times A=\set{(3,\pi), (4,\pi), (5,\pi),(3,2),(4,2),(5,2)}$
• Sea $\mathbb N=\set{0,1,2,4,\dotsi}$, y $\set{1,2}$
  $\set{1,2}\times \mathbb N =\set{(1,0),(1,1),(1,2),(1,3),\dotsc ,(2,0),(2,1),(2,2),(2,3)\dotsc }$}
  

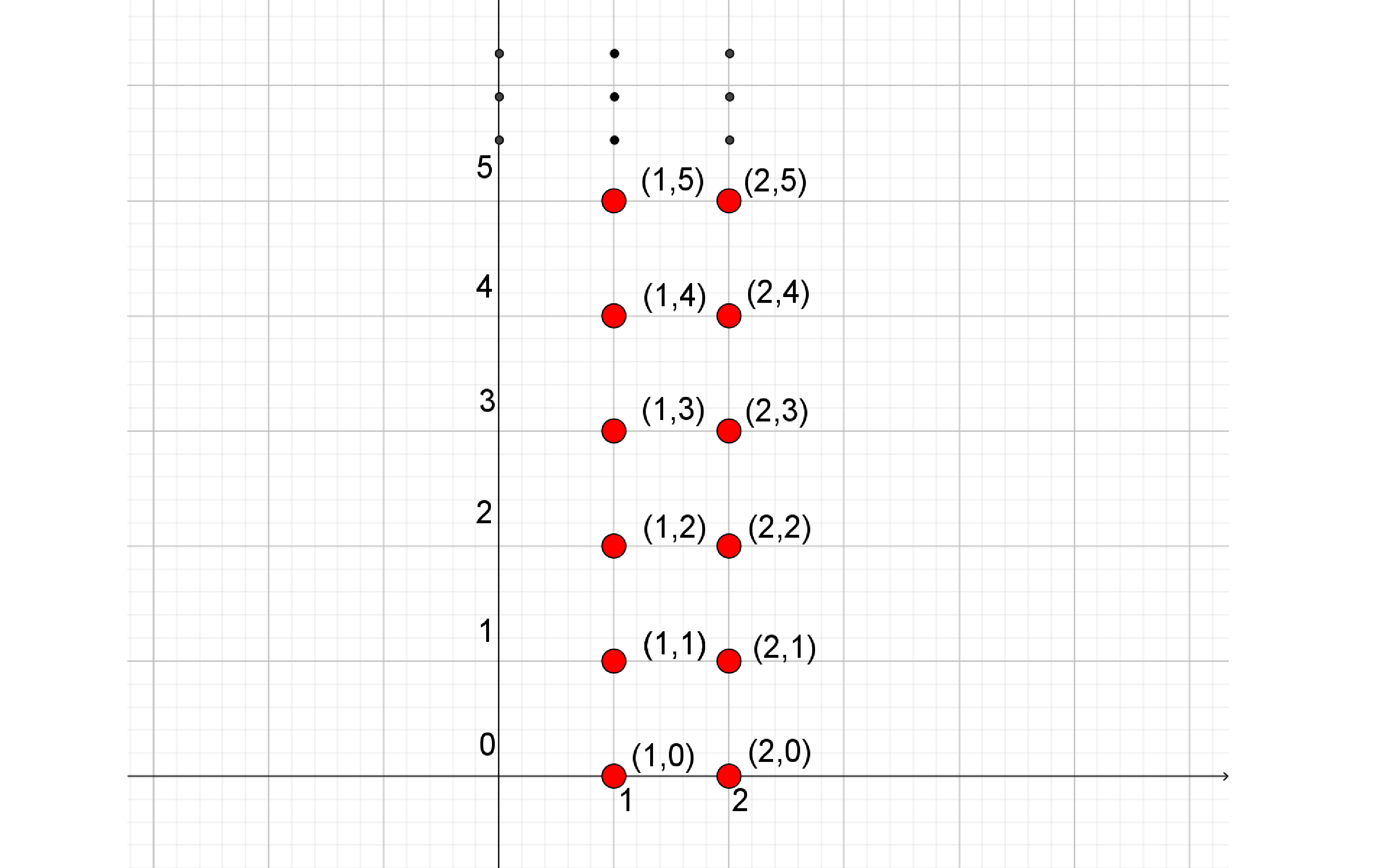
• $\mathbb R\times \mathbb R=\set{(x,y)\mid x,y\in \mathbb R}$, y se denota por $\mathbb R^2$, que son las parejas ordenadas del plano cartesiano.

En el siguiente recurso de Geogebra da los conjuntos $A$ y $B$ y obtén una representación gráfica de los mismos.

Generalizando:

Si $A_1,\dotsi,A_n$ son conjuntos, $A_1\times \dotsi \times A_n = \set{(a_1,\dotsi,a_n)\mid a_i\in A_i,1\leq i\leq n)}$.

Si $A_1=\dotsi =A_n=A$, para algún conjunto $A$, el producto de esos $n$ conjuntos $A\times \dotsi \times A$ se denota como $ A^n$.

Tarea moral

1. Sean $A$ y $B$ conjuntos. Si $A\subseteq B$, ¿existe alguna relación de contención entre $\mathcal{P}(A)$ y $\mathcal{P}(B)$?.
2. Sean $A$ y $B$ conjuntos. Responde y justifica:
   a) ¿Son iguales $\mathcal{P}(A)\cup \mathcal{P}(B)$ y $\mathcal{P}(A\cup B)$?
   b) ¿Son iguales $\mathcal{P}(A)\cap \mathcal{P}(B)$ y $\mathcal{P}(A\cup B)$?
3. Sea $A=\set{5,\emptyset,\set{\emptyset},\set{\emptyset,4},\set{\pi}}$
   $B_1=\set{2,\set{5,\set{\emptyset}}}$
   $B_2=\set{\set{\pi},\set{5,\emptyset}}$
   $B_3=\set{5,\emptyset}$
   Encuentra al siguiente conjunto: $\mathcal{P}(A)\cap (B_1\cup (B_2\cup B_3))$
4. Dados $a$,$b$,$c$ objetos define la terna $(a,b,c)$ como el conjunto $\set{\set{a},\set{a,b},\set{a,b,c}}$.
   ¿Con esta definición de terna se cumple que $(a,b,c)=(d,e,f)$ si y sólo si $a=d$, $b=e$ y $c=f\text{?}$ Justifica tu respuesta.

Más adelante

En la nota siguiente definiremos lo que es una relación entre dos conjuntos, encaminados a dar una definición formal del concepto de función ampliamente usado en el mundo de las matemáticas.

Enlaces relacionados

Página principal del curso.

• Enlace a la nota anterior. Nota 5. Leyes de Morgan y la diferencia simétrica.
• Enlace a la nota siguiente. Nota 7. Relaciones y funciones.