(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta nota analizaremos las definiciones de lo que es una función inyectiva o uno a uno, suprayectiva, cuando el codominio y la imagen coincide, y las biyectivas, aquellas funciones que son inyectivas y suprayectivas al mismo tiempo. Terminaremos mostrando que el hecho de tener una función invertible es equivalente a ser una función biyectiva.
Definición
Sean $A$, $B$ conjuntos, $f:A\to B$ una función. Decimos que $f$ es una función inyectiva si para cada $x_1$, $x_2$ $\in A$ se tiene que:
$x_1\neq x_2$ implica que $f(x_1)\neq f(x_2)$
o de modo equivalente
$f(x_1)=f(x_2)$ implica que $x_1=x_2.$
Ejemplo 1
En este ejemplo veremos cómo aplicar la definición de inyectividad para mostrar cuándo una función es inyectiva.
Sea $f:\mathbb R\setminus \set{1}\to \mathbb R$ dada por $f(x)=\frac{x}{x-1}$

Sean $x_1,x_2\in \mathbb R\setminus \set{1}$ tales que $f(x_1)=f(x_2)$
$f(x_1)=f(x_2)$ $\Longrightarrow$
$\frac{x_1}{x_1-1}= \frac{x_2}{x_2-1}$ $\Longrightarrow$
$x_1(x_2-1)=x_2(x_1-1)$ $\Longrightarrow$
$x_1x_2-x_1=x_2x_1-x_2$ $\Longrightarrow$
$-x_1=-x_2$ $\Longrightarrow$
$x_1=x_2.$
Por lo tanto $f$ es inyectiva.
Ejemplo 2
En este ejemplo veremos cómo aplicar la definición de inyectividad para mostrar cuándo una función no es inyectiva.
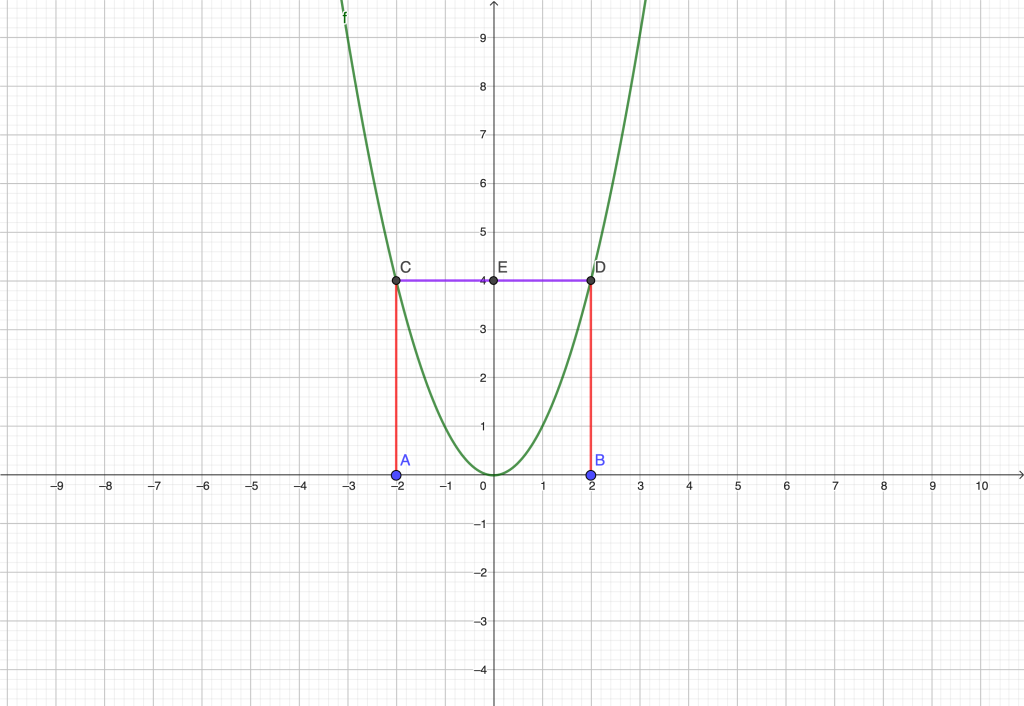
Sea $f:\mathbb{R} \to \mathbb{R}$ dada por $f(x) = x^2$. Sean $-2$ y $2$. Se tiene que $f(-2) = (-2)^2 = 4 = 2^2 = f(2)$. Si $f$ fuera inyectiva, para cada $x_1, x_2 \in \mathbb{R}$ se tendría que $f(x_1) = f(x_2)$ implicaría que $x_1 = x_2$. Sin embargo, $f(-2) = f(2)$ con $-2 \neq 2$. Concluimos entonces que $f$ no es inyectiva.
Notemos que para comprobar que una función $f$ no es inyectiva, basta con mostrar $x_1, x_2$ elementos distintos en el dominio de $f$ tales que $f(x_1)=f(x_2).$
Definición
Sean $A$, $B$ conjuntos, $f:A\to B$ una función. Decimos que $f$ es una función suprayectiva si para toda $y\in B$ existe $x\in A$ tal que $f(x)=y$, o de modo equivalente $Im\,f=B$.
Ejemplo 3
En este ejemplo veremos cómo aplicar la definición de suprayectividad para mostrar cuándo una función es suprayectiva.
Sea $f:\mathbb{R}\setminus\{2\} \to \mathbb{R}\setminus\{0\}$ dada por $f(x) = \frac{1}{x-2}$.

¿La función es suprayectiva?, ¿para toda $y\in\mathbb{R}\setminus\{0\} $, existe $x\in \mathbb R\setminus \set{2}$ tal que $f(x)=y$?
Consideremos entonces $y\in \mathbb{R}\setminus\{0\} $ y veamos si podemos hallar $x\in \mathbb R\setminus \set{2}$ tal que $f(x)=y$, pero de acuerdo a la regla de correspondencia de $f$ esto equivale a que $\frac{1}{x-2}=y.$ Analizando
$\frac{1}{x-2}=y\Leftrightarrow 1=y(x-2)\Leftrightarrow \frac{1}{y}=x-2\Leftrightarrow \frac{1}{y}+2=x.$
Notemos que la segunda equivalencia es posible gracias a que $y\in \mathbb{R}\setminus\{0\}$ y por lo tanto $y\neq 0$. Además, $\frac{1}{y}+2\neq 2$ pues si $\frac{1}{y}+2= 2$ tendríamos que $\frac{1}{y}=0$ y en consecuencia que $1=y(0)=0$ lo cual es una contradicción.
Por lo tanto, para cada $y\in \mathbb{R}\setminus\{0\} $ hemos hallado $x=\frac{1}{y}+2\in \mathbb R\setminus \set{2}$ tal que $f(x)=y$, probando con ello que $f$ es suprayectiva.
Ejemplo 4
En este ejemplo veremos cómo aplicar la definición de suprayectividad para mostrar cuándo una función no es suprayectiva.
$f:\mathbb R\setminus \set{-5}\to \mathbb R$ dada por $f(x)=\frac{2}{x+5}+1$
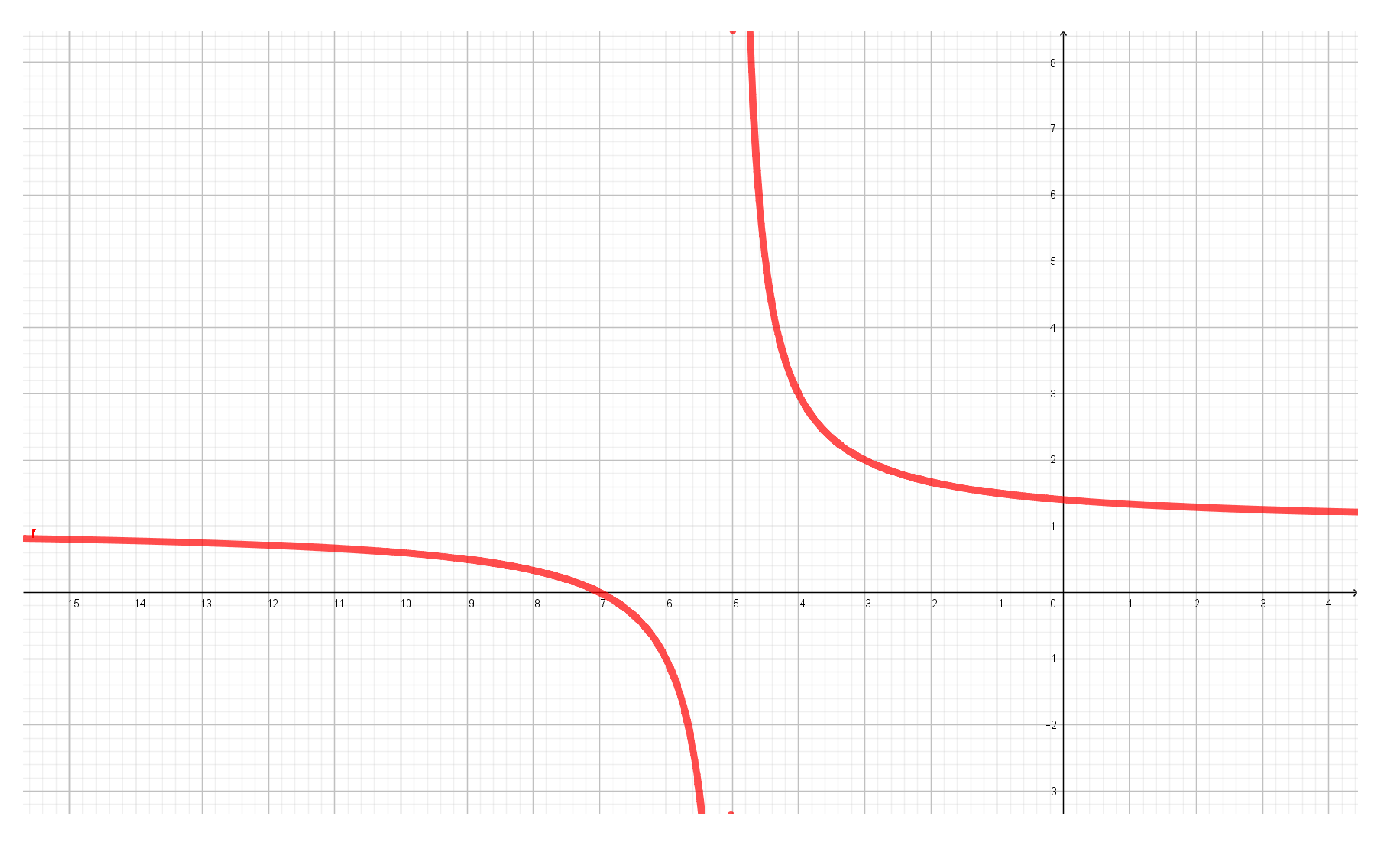
¿La función es suprayectiva?, Para toda $y\in \mathbb R$, ¿existe $x\in \mathbb R\setminus \set{-5}$ tal que $f(x)=y$?
Supongamos que sí es suprayectiva, entonces para toda $y\in \mathbb R$, existe $x\in \mathbb R\setminus \set{-5}$ tal que $f(x)=1=y$. Analizando
$y=\frac{2}{x+5}+1\Leftrightarrow y-1=\frac{2}{x+5}.$
En este punto notamos que hay dos opciones, $y=1$ o $y\neq 1$. Notemos que para $y=1$ completando las equivalencias anteriores tendríamos
$1=\frac{2}{x+5}+1\Leftrightarrow 0=\frac{2}{x+5}\Leftrightarrow 0(x+5)=2\Leftrightarrow0=2,$
pero $0\neq 2$ así que concluimos que no existe $x\in \mathbb R\setminus \set{-5}$ tal que $f(x)=1$ y, por lo tanto, $f$ no es suprayectiva.
Notemos que para mostrar que una función no es supreyectiva basta exhibir algún $y$ en el codominio de $f$ tal que no exista $x$ en el dominio de $f$ con $f(x)=y$.
Definición
Sean $A,B$ conjuntos $f:A\to B$ una función. Decimos que $f$ es biyectiva si $f$ es inyectiva y suprayectiva.
Teorema
Una función es invertible si y sólo si es biyectiva.
Demostración
$\Longrightarrow$ Demostración de la implicación de ida
Supongamos que $f$ es invertible.
Por demostrar que es biyectiva.
Como $f$ es invertible, existe $f^{-1}:B\to A$ la inversa de $f$.
Veamos que $f$ es inyectiva.
Sean $x_1,x_2\in A$ tales que $f(x_1)=f(x_2)$
Como $f(x_1)=f(x_2)$ y $f^{-1}$ es una función sabemos que $f^{-1}(f(x_1))= f^{-1}(f(x_2))$, lo que por la definición de composición de funciones es equivalente a que $f^{-1}\circ f(x_1)= f^{-1}\circ f(x_2).$ Pero debido a que $f^{-1}$ es la función inversa de $f$ tenemos que $id_A(x_1)=id_B(x_2)$ y por la regla de correspondencia de las funciones identidad esto equivale a que $x_1=x_2.$
Por lo tanto, $f$ es inyectiva.
Para ver que $f$ es suprayectiva, sea $y\in B$ y veamos que hay un elemento $x$ en $A$ tal que $f(x)=y$. Consideremos $f^{-1}(y)\in A$, al aplicarle $f$ tenemos que:
$f(f^{-1}(y))=f\circ f^{-1}(y) = id_B(y)=y$.
Así, $f$ es suprayectiva.
$\Longleftarrow$ Demostración de la implicación de regreso
Supongamos que $f$ es biyectiva
Por demostrar que es invertible.
Dado $y\in B$, por ser $f$ suprayectiva, existe $x\in A$ tal que $f(x)=y$, además como $f$ es inyectiva dicha $x$ es única, llamémosle $x_y$.
Definimos $g:B\to A$ con $g(y)=x_y$, donde $x_y$ es el único elemento de $A$ tal que $f(x_y)=y$.
Como $g$ asigna a cada $y\in B$ un único elemento de $A$, entonces $g$ es una función.
Veamos ahora que $g$ es una inversa de $f$.
Dado $y\in B$ se tiene que
$f\circ g(y)=f(g(y))=f(x_y)=y$, y así $f\circ g=id_B.$
Dado $x\in A$ se tiene que
$g\circ f(x)=g(f(x))=x_{f(x)}$, el único elemento en $A$ que bajo $f$ nos da $f(x)$, pero $x\in A$ es tal que bajo $f$ da $f(x)$. Así, $x_{f(x)}=x$ y entonces $g\circ f(x)=x$, por lo tanto, $g\circ f=id_A$.
Así, $g$ es una inversa de $f$ y concluimos que $f$ es invertible.
$\square$
Tarea Moral
1. Prueba o da un contraejemplo:
i) Sean $f:A\to B$, $g:B\to C$ tales que $g\circ f$ es inyectiva, ¿Es $f$ necesariamente inyectiva?
ii) Sean $f:A\to B$, $g:B\to C$ tales que $g\circ f$ es inyectiva, ¿Es $g$ necesariamente inyectiva?
2. Prueba o da un contraejemplo:
i) Sean $f:A\to B$, $g:B\to C$ tales que $g\circ f$ es suprayectiva, ¿Es $f$ necesariamente suprayectiva ?
ii) Sean $f:A\to B$, $g:B\to C$ tales que $g\circ f$ es suprayectiva, ¿Es $g$ necesariamente suprayectiva ?
3. Determina si las siguientes funciones son inyectivas, suprayectivas o biyectivas.
i) $f:\mathbb R\to (-\infty,3]$ con $f(x)=x^2+3$
ii) $f:[1,\infty)\to [0,\infty)$ con $f(x)=4(x-1)^2$
iii) $f:\set{x\in \mathbb R\mid x\neq -\frac{5}{3}}\to \mathbb R$ con $f(x)=\frac{1}{3x+5}$.
iv) $f:\set{x\in \mathbb R\mid x\neq 7}\to \set{x\in \mathbb R\mid x\neq 1}$ con $f(x)=\frac{1}{x-7}+1$.
Más adelante
En la siguiente nota daremos algunos teoremas referentes a la composición de funciones inyectivas con inyectivas y suprayectivas con suprayectivas.
Enlaces relacionados
- Enlace a la nota anterior. Nota 10. Función inversa.
- Enlace a la nota siguiente. Nota 12. Teoremas de la composición de funciones inyectivas, suprayectivas y biyectivas.
