(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta nota analizaremos las definiciones de lo que es una función inyectiva o uno a uno, suprayectiva o aquella que tiene su codominio lleno, y las biyectivas, aquellas funciones que son inyectivas y suprayectivas al mismo tiempo, terminaremos mostrando que el hecho de tener una función invertible es equivalente a tener una función biyectiva.
Definición
Sean $A$, $B$ conjuntos, $f:A\to B$ una función. Si para cada $x_1$, $x_2$ $\in A$ se tiene que:
$x_1\neq x_2$ implica que $f(x_1)\neq f(x_2)$
O de modo equivalente
$f(x_1)=f(x_2)$ implica que $x_1=x_2$
decimos que $f$ es una función inyectiva.
Ejemplo
Sea $f:\mathbb R\setminus \set{1}\to \mathbb R$ dada por $f(x)=\frac{x}{x-1}$

Sean $x_1,x_2\in \mathbb R\setminus \set{1}$ tales que $f(x_1)=f(x_2)$
$f(x_1)=f(x_2)$ $\Longrightarrow$
$\frac{x_1}{x_1-1}= \frac{x_2}{x_2-1}$ $\Longrightarrow$
$x_1(x_2-1)=x_2(x_1-1)$ $\Longrightarrow$
$x_1x_2-x_1=x_2x_1-x_2$ $\Longrightarrow$
$-x_1=-x_2$ $\Longrightarrow$
$x_1=x_2$
Y por lo tanto $f$ es inyectiva.
Definición
Sean $A$, $B$ conjuntos, $f:A\to B$ una función. Decimos que $f$ es una función suprayectiva si para toda $y\in B$ existe $x\in A$ tal que $f(x)=y$, o de modo equivalente $Im\,f=B$.
Ejemplo
$f:\mathbb R\setminus \set{-5}\to \mathbb R$ dada por $f(x)=\frac{2}{x+5}+1$
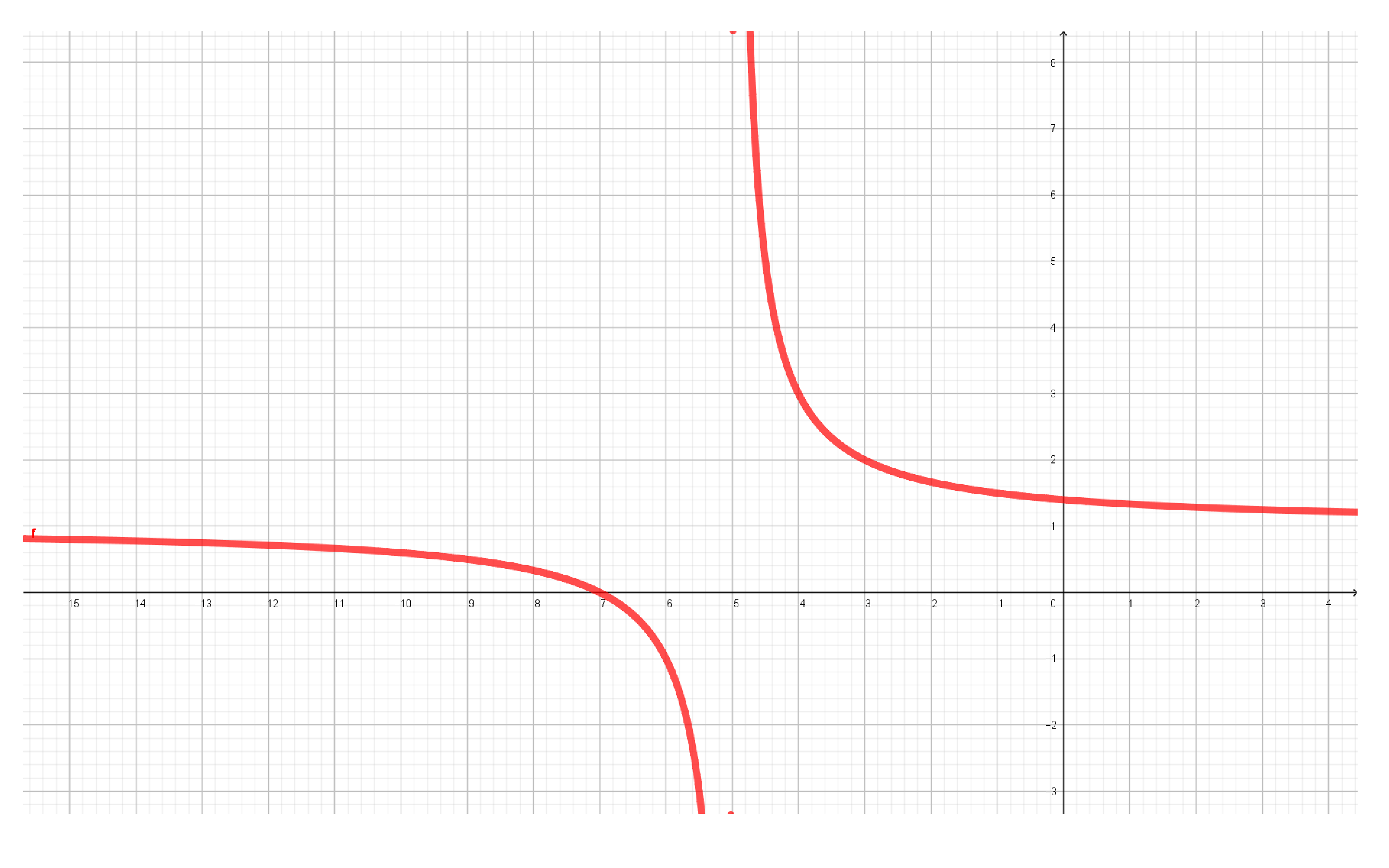
¿La función es suprayectiva?, Para toda $y\in \mathbb R$, ¿existe $x\in \mathbb R\setminus \set{-5}$ tal que $f(x)=y$?
Supongamos que sí es suprayectiva, entonces para $y=1$, existe $x\in \mathbb R\setminus \set{-5}$ tal que $f(x)=1=y$
$1=\frac{2}{x+5}+1$ $\Longrightarrow$
$0=\frac{2}{x+5}$ $\Longrightarrow$
$(x+5)0=2$ $\Longrightarrow$
$0=2$, lo cual es una contradicción.
Así no existe $x\in \mathbb R\setminus \set{-5}$ tal que $f(x)=y=1$ y por lo tanto $f$ no es suprayectiva.
Definición
Sean $A,B$ conjuntos $f:A\to B$ una función. Decimos que $f$ es biyectiva si $f$ es inyectiva y suprayectiva.
Teorema
Una función es invertible si y solosi es biyectiva.
Demostración
$\Longrightarrow$ Demostración de la implicación de ida
Supongamos que $f$ es invertible.
Por demostrar que es biyectiva.
Si $f$ es invertible entonces existe $f^{-1}:B\to A$ la inversa de $f$.
Veamos que $f$ es inyectiva.
Sean $x_1,x_2\in A$ tales que $f(x_1)=f(x_2)$
$f(x_1)=f(x_2)$ $\Longrightarrow$
$f^{-1}(f(x_1))= f^{-1} (f(x_2))$ $\Longrightarrow$
$f^{-1}\circ f(x_1)= f^{-1}\circ f(x_2)$ $\Longrightarrow$
$id_A(x_1)=id_B(x_2)$ $\Longrightarrow$
$x_1=x_2$
Y por lo tanto $f$ es inyectiva.
Para ver que $f$ es suprayectiva, Sea $y\in B$, tenemos que mostrar que hay un elemento en $A$ tal que bajo $f$ va a dar a $y\in B$, consideramos $f^{-1}(y)\in A$ y al aplicarle $f$ tenemos que:
$f(f^{-1}(y))=f\circ f^{-1}(y) = id_B(y)=y$, y por lo tanto $f$ es suprayectiva.
$\Longleftarrow$ Demostración de la implicación de regreso
Supongamos que $f$ es biyectiva
Por demostrar que es invertible.
Dado $y\in B$ por ser $f$ suprayectiva existe $x\in A$ tal que $f(x)=y$, además como $f$ es inyectiva dicha $x$ es única, llamémosle $x_y$.
Definimos $g:B\to A$ con $g(y)=x_y$, donde $x_y$ es el único elemento de $A$ tal que $f(x_y)=y$.
Como $g$ asigna a cada $y\in B$ un único elemento de $A$, entonces $g$ es una función.
Veamos ahora que $g$ es una inversa de $f$.
Dado $y\in B$ se tiene que
$f\circ g(y)=f(g(y))=f(x_y)=y$, y así $f\circ g=id_B.$
Dado $x\in A$ se tiene que
$g\circ f(x)=g(f(x))=x_{f(x)}$, el único elemento en $A$ que bajo $f$ nos da $f(x)$, pero $x\in A$ es tal que bajo $f$ da $f(x)$. Así $x_{f(x)}=x$ y entonces $g\circ f(x)=x$, por lo tanto $g\circ f=id_A$.
Así $g$ es una inversa de $f$ y concluimos que $f$ es invertible.
$\square$
Tarea Moral
1. Prueba o da un contraejemplo:
i) Sean $f:A\to B$, $g:B\to C$ tales que $g\circ f$ es inyectiva, ¿Es $g\circ f$ necesariamente inyectiva?.
ii) Sean $f:A\to B$, $g:B\to C$ tales que $f$ es inyectiva, ¿Es $g\circ f$ necesariamente inyectiva?.
2. Prueba o da un contraejemplo:
i) Sean $f:A\to B$, $g:B\to C$ tales que $g\circ f$ es suprayectiva, ¿Es $g\circ f$ necesariamente suprayectiva ?.
ii) Sean $f:A\to B$, $g:B\to C$ tales que $g$ es suprayectiva , ¿Es $g\circ f$ necesariamente suprayectiva?.
3. Determina si las siguientes funciones son inyectivas, suprayectivas o biyectivas.
i) $f:\mathbb R\to (-\infty,3]$ con $f(x)=x^2+3$
ii) $f:[1,\infty)\to [0,\infty)$ con $f(x)=4(x-1)^2$
iii) $f:\set{x\in \mathbb R\mid x\neq -2}\to \mathbb R$ con $f(x)=\frac{1}{x+2}$.
iv) $f:\set{x\in \mathbb R\mid x\neq 7}\to \set{x\in \mathbb R\mid x\neq 1}$ con $f(x)=\frac{1}{x-7}+1$.
Más adelante
En la siguiente nota daremos algunos teoremas referentes a la composición de funciones inyectivas con inyectivas y suprayectivas con suprayectivas, además veremos que es lo mismo ser biyectiva que invertible.
Enlaces relacionados
- Enlace a la nota anterior. Nota 10. Función inversa.
- Enlace a la nota siguiente. Nota 12. Teoremas de la composición de funciones inyectivas, suprayectivas y biyectivas.
