(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta nota centraremos nuestros esfuerzos en comprender el concepto de función inversa, primero veremos la definición de lo que es una función inversa derecha o izquierda de una función, para después definir con ello lo que es una función invertible.
Definición
Sean $A$, $B$ conjuntos, $f:A\to B$, $g:B\to A$ funciones.
Si $g\circ f=id_A$, decimos que $f$ es una inversa derecha de $g$ y que $g$ es una inversa izquierda de $f$.
Decimos que $f$ es invertible si existe una función $g$ que sea inversa izquierda y derecha de $f$; en este caso se dice que $g$ es una inversa de $f$.
Ejemplos
El siguiente ejemplo aparece en el libro de Avella y Campero mencionado en la bibliografía, Ejemplo 4.56, página 193:
1. Sean $f:\set{1,2,3}\to \set{4,5,6,7}$ con:
$f(1)=4$, $f(2)=5$, $f(3)=6$
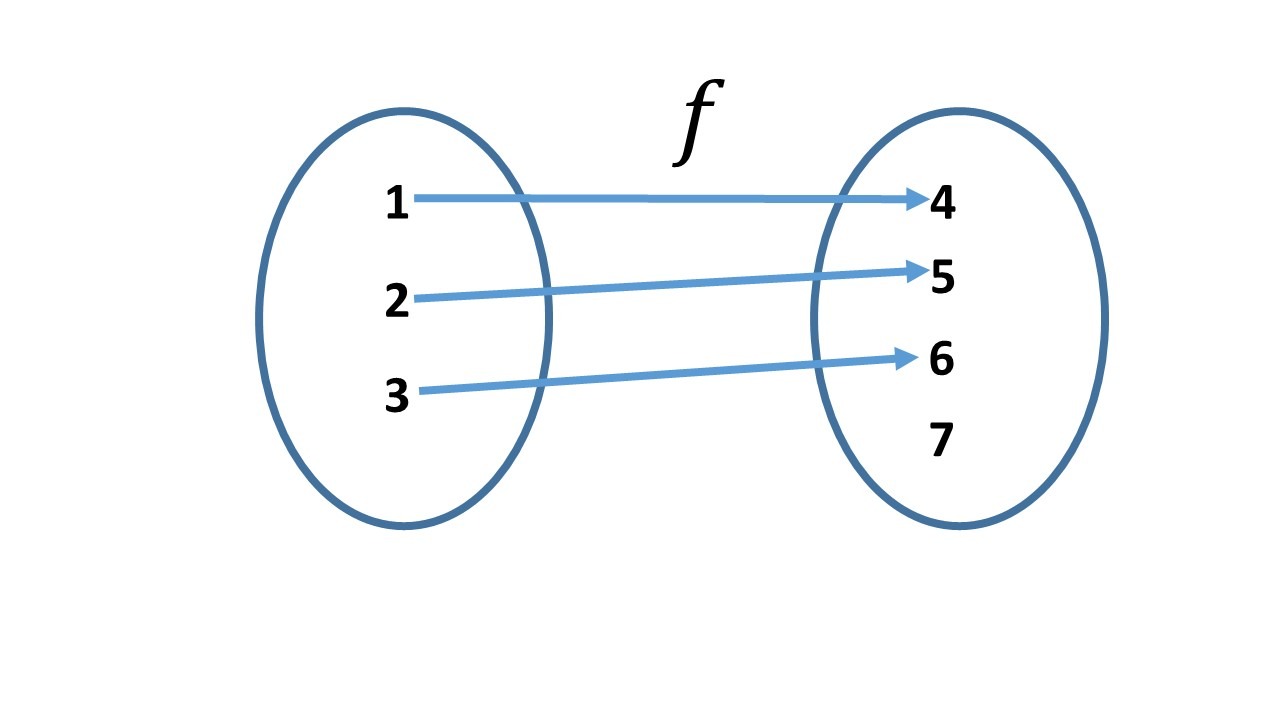
y $g:\set{ 4,5,6,7 }\to \set{1,2,3}$ con:
$g(4)=1$, $g(5)=2$, $g(6)=3$, $g(7)=3.$
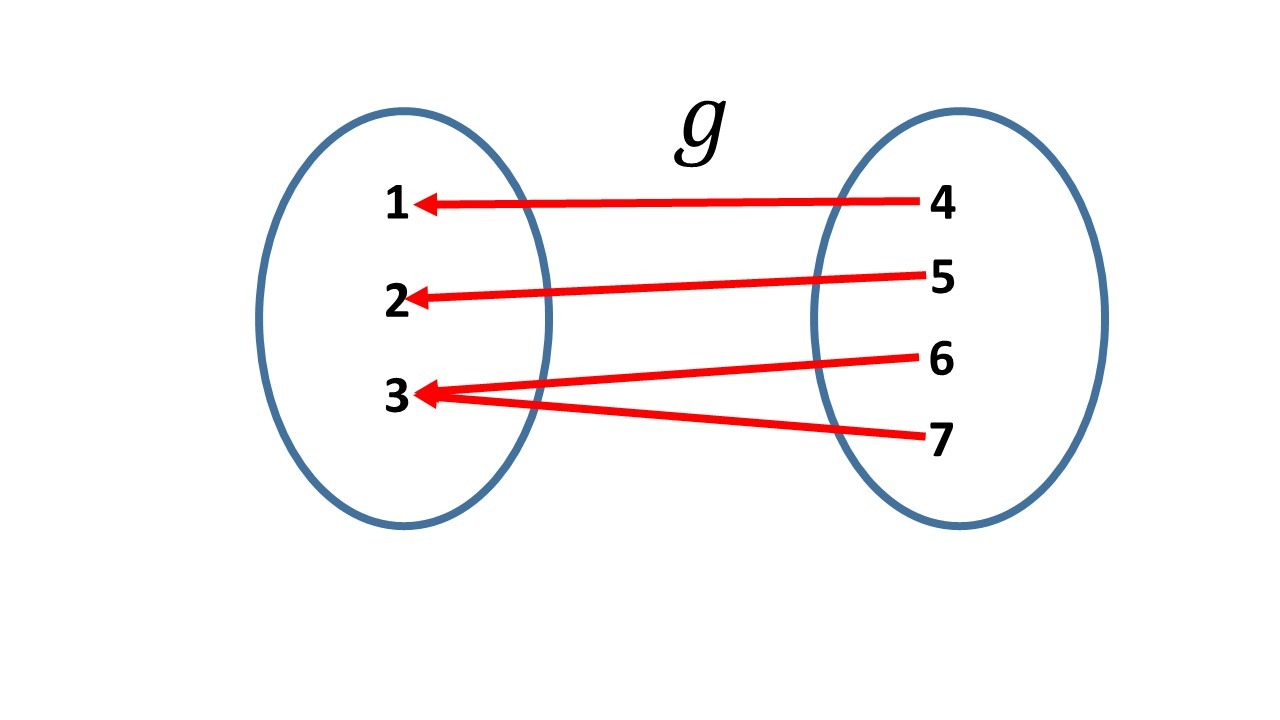
Si se hace la composición $g\circ f$:
$g\circ f(1)=g(f(1))=g(4)=1$
$g\circ f(2)=g(f(2))=g(5)=2$
$g\circ f(3)=g(f(3))=g(4)=3.$
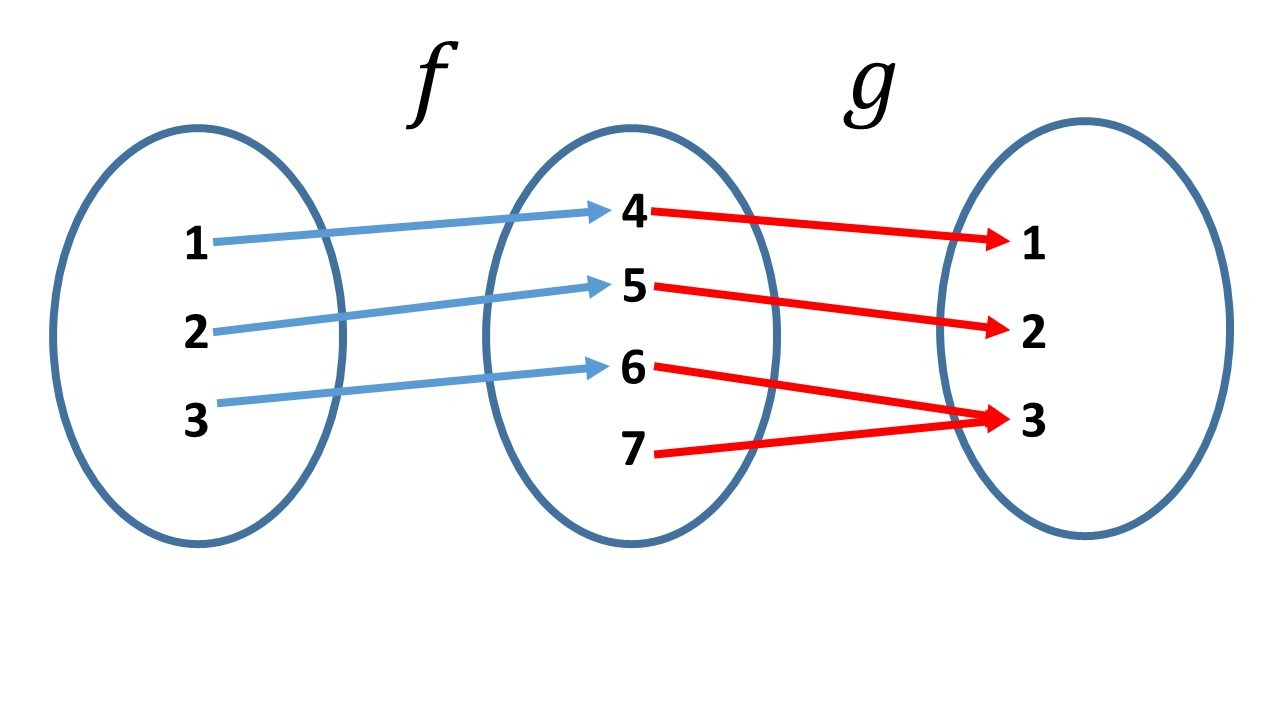
Así, $g\circ f=id_{\set{1,2,3}}$, de forma que $g$ es una inversa izquierda de $f$ y $f$ es una inversa derecha de $g$.
Pero $f\circ g\neq id_{\set{4,5,6,7}}$, pues $f\circ g(7)=f(g(7))=f(3)=6$, y por lo tanto $g$ no es una inversa derecha de $f$ y $f$ no es una inversa izquierda de $g$.
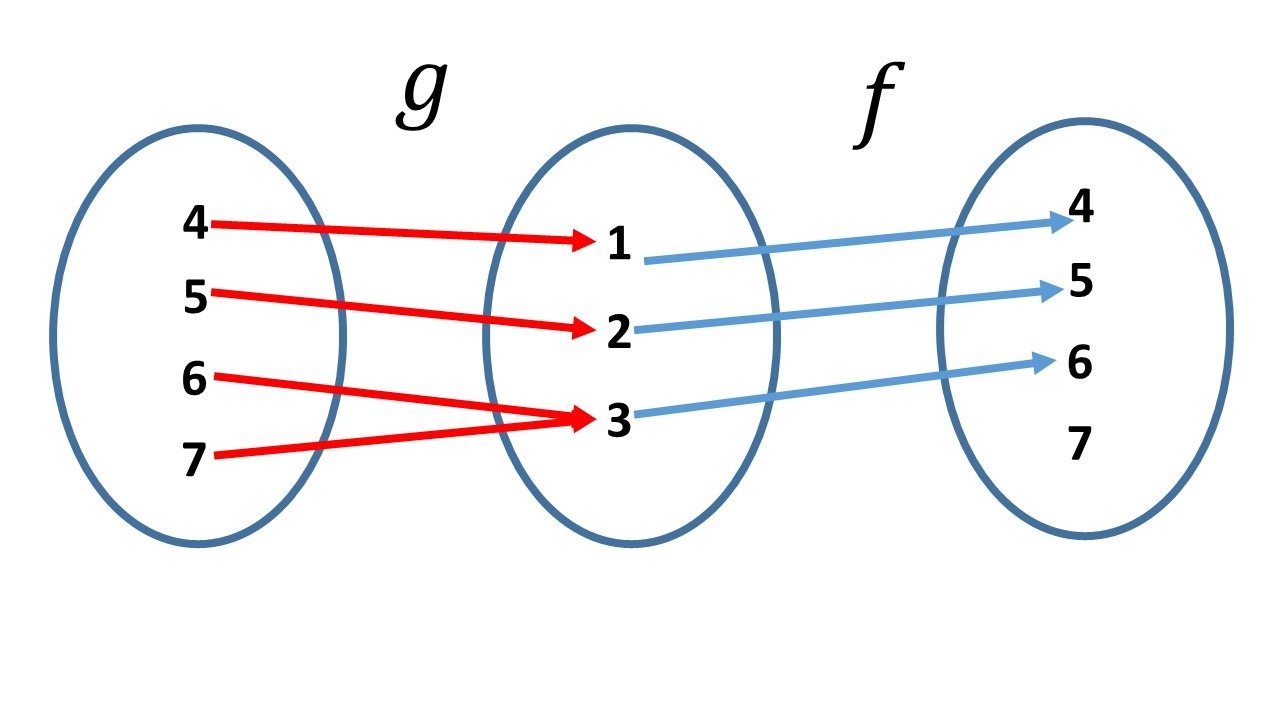
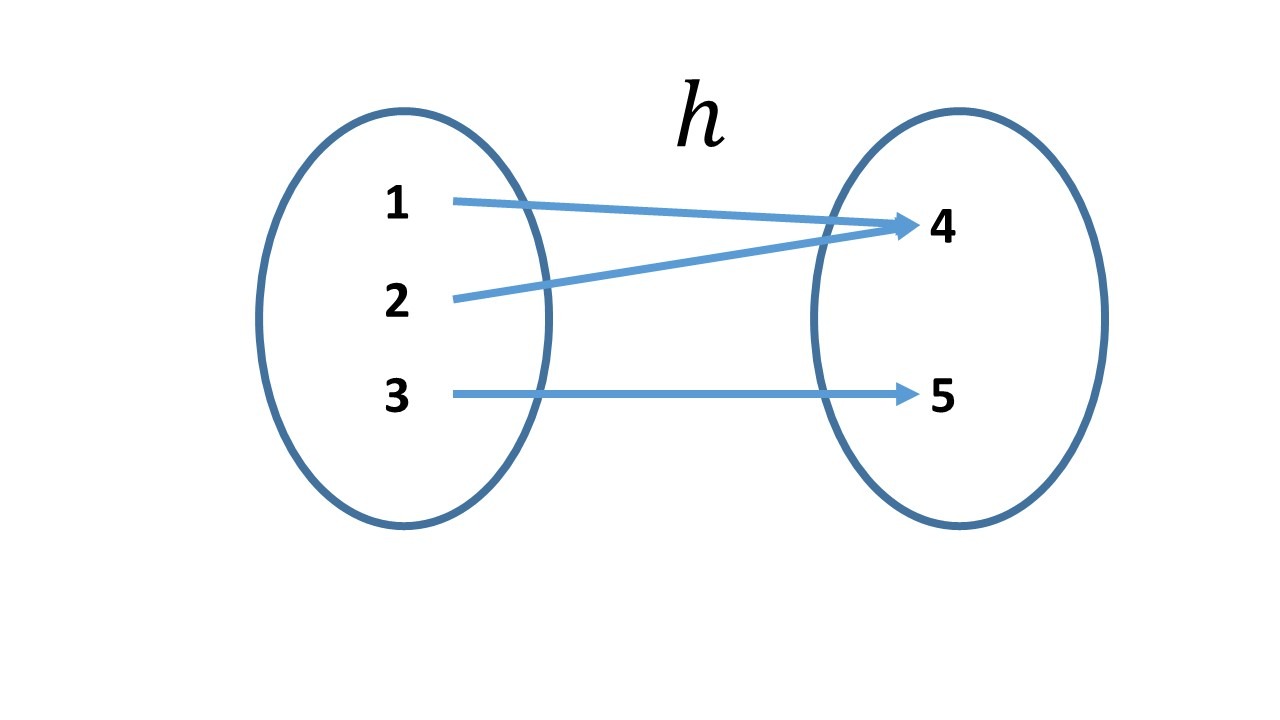
2. Sean $h:\set{1,2,3}\to \set{4,5}$ con:
$h(1)=2$, $h(2)=4$, $h(3)=5$
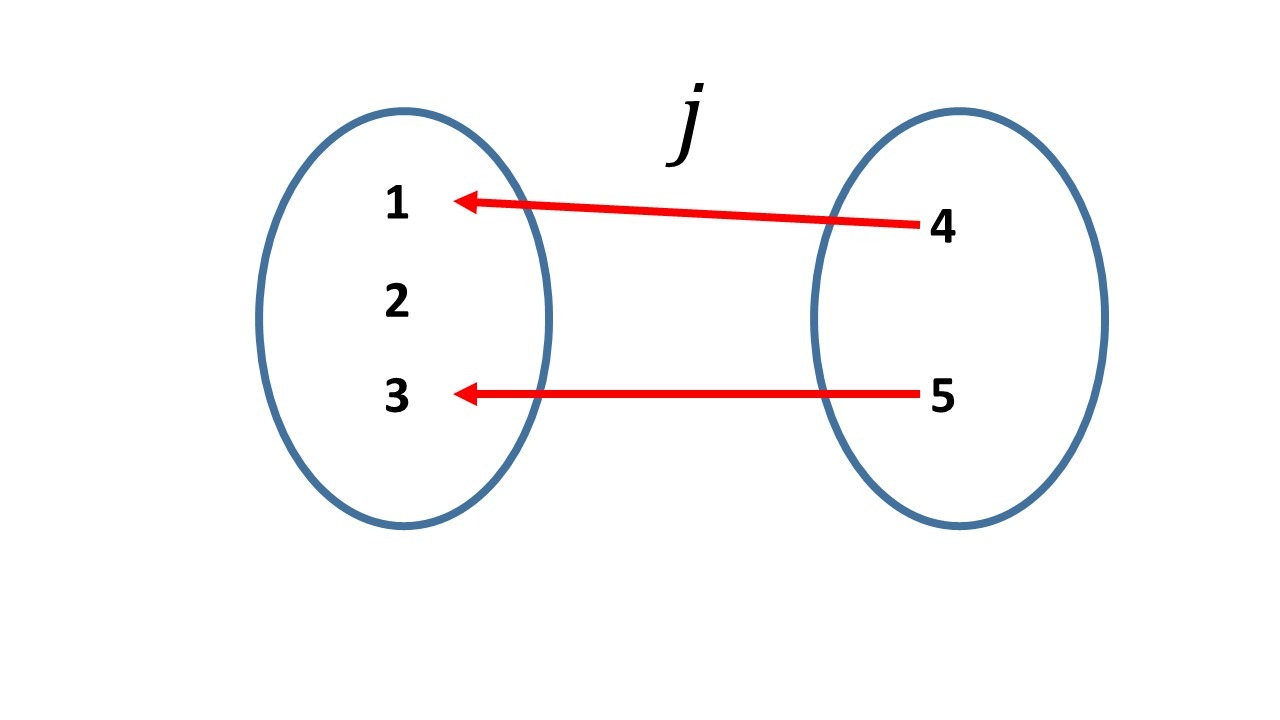
y $j:\set{4,5}\to \set{1,2,3}$ con:
$j(4)=1$, $j(5)=3.$
Como:
$h\circ j(4)=h(j(4))=h(1)=4$,
$h\circ j(5)=h(j(5))=h(3)=5$,
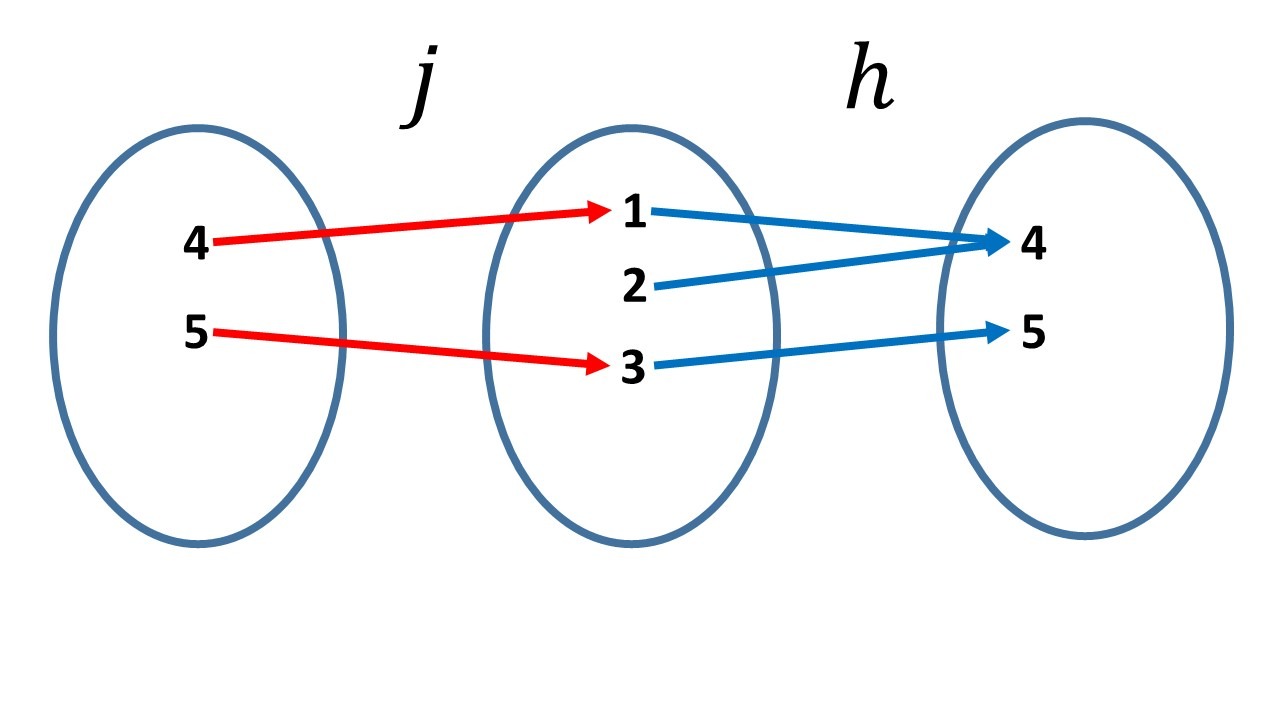
Notamos que $h\circ j=id_{\set{4,5}}$, pero $j\circ h\neq id_{\set{1,2,3}}$ pues $j\circ h(2)=1$.
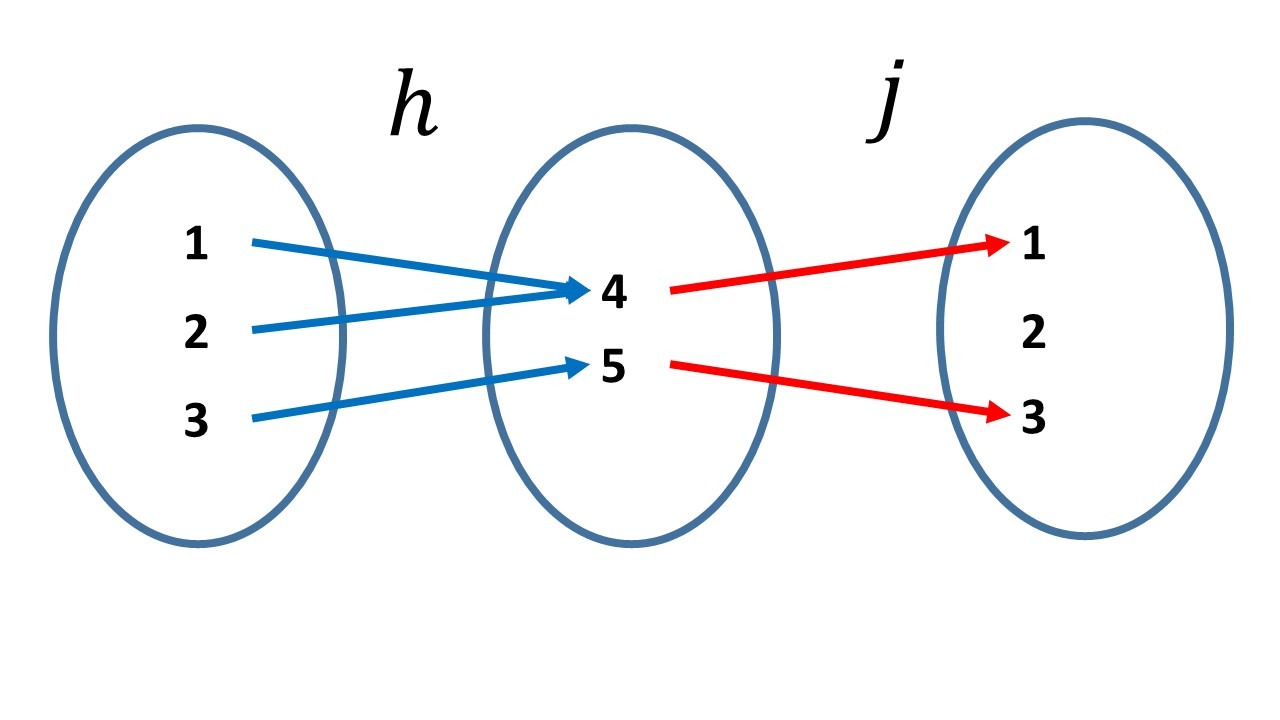
Así, $h$ es una inversa izquierda de $j$, $j$ es una inversa derecha de $h$, pero $h$ no es una inversa derecha de $j$ y $j$ no es una inversa izquierda de $h$.
Teorema
Sean $A$, $B$ conjuntos, $f:A\to B$ una función. Si $f$ tiene un inverso derecho $g$ y un inverso izquierdo $h$, entonces $g=h$.
Demostración
Sean $A$ y $B$ conjuntos y $f:A\to B$ una función. Supongamos que existen $g$ un inverso derecho de $f$ y $h$ un inverso izquierdo de $f$.
Como $g$ es un inverso derecho de $f$, por definición $g$ es una función $g:B\to A$ tal que $f\circ g=id_B$.
Como $h$ es un inverso izquierdo de $f$, por definición $h$ es una función $h:B\to A$ tal que $h\circ f=id_A$.
Queremos demostrar que $h=g.$
| $h=$ | empezamos tomando la función $h$ |
| $h\circ id_B=$ | la reescribimos de esta forma, expresándola como la identidad en $B$ compuesta con $h$ |
| $h\circ (f\circ g)=$ | por hipotesis $id_B=f\circ g$ |
| $(h\circ f)\circ g=$ | por asociatividad de la composición de funciones |
| $id_A\circ g=$ | por hipotesis $id_A=h\circ f$ |
| $g$ | la composición con la identidad nos da $g$ |
$\square$
Corolario
Si una función $f$ es invertible, entonces su inverso es único. En este caso su inverso se denota por $f^{-1}$.
Demostración
Sea $f$ una función invertible. Supongamos que $g$ y $h$ son inversos de $f$. En particular $g$ es un inverso derecho de $f$ y $h$ es un inverso izquierdo de $f$. Así, por el teorema anterior $g=h$.
$\square$
Tarea Moral
En cada inciso determina si existe una inversa derecha de $f$, o bien una inversa izquierda de $f$.
En caso de que exista constrúyela.
1. $f:\set{3,4,7,8}\to \set{1,2,7,8,9}$ con
$f(3)=9$, $f(4)=8$, $f(7)=7$, $f(8)=2$.
2. $f:\set{-2,-1,0,1,2}\to \set{3,6,9}$ con
$f(-2)=f(2)=3$, $f(1)=f(-1)=6$, $f(0)=9$.
3. $f:\set{0,2,4,6}\to \set{1,3,5,7}$ con
$f(x)=x+1$.
4. $f:\set{1,2,3}\to \set{5,6,7}$ con
$f(1)=f(2)=5$, $f(3)=7$.
5. Utiliza el siguiente recurso de geogebra para obtener la función inversa de algunas funciones.
Más adelante
En la siguiente nota analizaremos las definiciones de funciones inyectivas, suprayectivas y biyectivas.
Enlaces relacionados
- Enlace a la nota anterior. Nota 9. Composición de funciones.
- Enlace a la nota siguiente. Nota 11. Funciones inyectivas, suprayectivas y biyectivas.
Agradecemos a Erwin Cortés por el recurso de GeoGebra.
