Introducción

En la entrada anterior definimos a la exponencial compleja y vimos que dicha función extiende a la función exponencial real, por lo que comparten ciertas propiedades. Sin embargo, vimos que esta nueva función cumple propiedades que no se tienen en su versión real, entre ellas la periodicidad, razón por la cual esta función no es inyectiva en $\mathbb{C}$.

Nuestro objetivo en esta entrada será definir a la función logaritmo complejo de tal modo que obtengamos una «función inversa» para la exponencial compleja. Como veremos esta función requerirá cierta sutileza pues será una función multivaluada.

En nuestros cursos de Cálculo y/o Análisis se verifica que para $a>1$ y para toda $x,y\in \mathbb{R}$ se cumple que: $$\begin{array}{r}{a}^x{a}^y=a^{x+y},\\ {\left(a^x\right)}^y=a^{xy}.\end{array}$$

Además se prueba que la función $f:\mathbb{R}\to {\mathbb{R}}^{+}$ dada por $f(x)=a^x$ es biyectiva y se define a su inversa como el logaritmo de $y$ en base $a$, denotado como ${\log }_a(y)$.

Motivados en esto, nos gustaría definir una función inversa para la función exponencial compleja que extienda la definición de la función logaritmo real. Sin embargo, dado que la función exponencial compleja no es inyectiva en $\mathbb{C}$, debemos dar una definición precisa para la función logaritmo complejo, con el fin de evitar cualquier ambigüedad.

Supongamos que queremos resolver la ecuación $e^w=z$. La primera pregunta que podemos hacernos es si existe solo una solución. Por ejemplo, si planteamos $e^w=i$, no es difícil verificar que $w_1=i{\displaystyle \frac{\pi }{2}}$, $w_2=i{\displaystyle \frac{5\pi }{2}}$ y $w_3=–i{\displaystyle \frac{3\pi }{2}}$ son soluciones de esta ecuación.

De acuerdo con la proposición 20.3 de la entrada anterior, sabemos que la función exponencial compleja es suprayectiva en $\mathbb{C}\setminus 0$, por lo que para $z=0$ la ecuación planteada no tendrá solución. Supongamos entonces que $z\ne 0$. Veamos que en tal caso dicha ecuación tiene infinitas soluciones.

Primeramente, recordemos que queremos definir a la función logaritmo complejo, denotada por $\log (z)$, como la inversa de la función exponencial compleja. Para $z\ne 0$, si hacemos $w=\log (z)$, entonces podemos plantear: $$w=\log (z)\iff e^w=z,$$ para determinar a $w$ en términos de $z$.

Haciendo $w=u+iv$ y $z=r{e}^{i\theta }$, con $r=|z|>0$ y $\theta =\mathrm{Arg}(z)$, entonces tenemos que: $$e^w=z⟺e^{u+iv}=e^u{e}^{iv}=r{e}^{i\theta }⟺\{\begin{array}{l}|e^w|=|z|\\ \\ \arg \left(e^w\right)=\arg \left(z\right),\end{array}$$ de donde: $$e^u=r\text{y}v+2\pi n_1=\theta +2\pi n_2,n_1,n_2\in \mathbb{Z}.$$

De la primera expresión tenemos que $u=\ln (r)$, donde $\ln (x)$ denota la función real logaritmo natural, $x\in {\mathbb{R}}^{+}$.

Por otra parte, de la segunda ecuación tenemos que: $$v=\theta +2\pi k=\mathrm{Arg}(z)+2\pi k,k=n_2–n_1\in \mathbb{Z},$$ es decir $v=\arg (z)$.

Dado que la función $G(z)=\arg (z)$ es multivaluada, entonces existen infinitas soluciones para la ecuación $e^w=z$, con $z=r{e}^{i\theta }\ne 0$, las cuales están dadas por: $$w=\ln (r)+i\arg (z).$$

Lo anterior nos motiva a dar la siguiente:

Definición 21.1. (Logaritmo complejo.)
Sea $z\in \mathbb{C}\setminus \{0\}$. Definimos a la función multivaluada logaritmo complejo, denotada por $\log (z)$, como: $$\begin{array}{rl}\log (z)& =\ln |z|+i\arg (z)\\ & =\ln (r)+i(\theta +2\pi k),k\in \mathbb{Z},\end{array}$$ donde $r=|z|>0$ y $\theta =\mathrm{Arg}(z)$.

Observación 21.1.
Notemos que en la definición anterior no es necesario que $\theta$ sea el argumento principal, en realidad basta con que sea cualquier argumento que permita representar a $z\ne 0$ en su forma exponencial, es decir $z=r{e}^{i\theta }$.

Definición 21.2. (Rama principal del logaritmo complejo.)
Sea $z\in \mathbb{C}\setminus \{0\}$. Definimos a la rama principal del logaritmo complejo, denotada por $\mathrm{Log}(z)$, como: $$\mathrm{Log}(z)=\ln |z|+i\mathrm{Arg}(z),$$ la cual es una función univaluada.

Verificar que $\mathrm{Log}(z)$ es univaluada es sencillo si recordamos la definición 20.3 y la proposición 13.2, ya que si $z=r{e}^{i\theta }\ne 0$, con $r=|z|$ y $\theta =\mathrm{Arg}(z)$, entonces: $$\begin{array}{rl}\mathrm{Log}(z(r,\theta +2\pi ))& =\mathrm{Log}\left(r{e}^{i\theta +2\pi }\right)\\ & =\ln (r)+i\mathrm{Arg}\left(r{e}^{i\theta +2\pi }\right)\\ & =\ln (r)+i(\theta +2\pi +2\pi (-1))\\ & =\ln (r)+i\theta \\ & =\mathrm{Log}\left(r{e}^{i\theta }\right)\\ & =\mathrm{Log}(z(r,\theta )).\end{array}$$

Observación 21.2.
Debe ser claro que $\mathrm{Log}(z)$ determina un valor particular de $\log (z)$, para el cual su parte imaginaria es tal que $\mathrm{Arg}(z)\in (-\pi ,\pi ]$. De acuerdo con la definición 21.1 tenemos que: $$\log (z)=\mathrm{Log}(z)+i2\pi k,k\in \mathbb{Z},$$ es decir que los valores de $\log (z)$ difieren de la rama principal en $i2k\pi$.

Ejemplo 21.1.
Determinemos los siguientes logaritmos:
a) $\log (i)$.
b) $\log (5)$.
c) $\log (-2)$.
d) $\mathrm{Log}(\sqrt{3}+i)$.

Solución. De acuerdo con la observación 21.2, en los cuatro incisos basta con determinar la rama principal del logaritmo.

a) Sabemos que para $z=i$ tenemos que $|z|=1$ y $\mathrm{Arg}(z)=\frac{\pi }{2}$, por lo que: $$\mathrm{Log}(i)=\ln (1)+i\frac{\pi }{2}=0+i\frac{\pi }{2}=i\frac{\pi }{2}.$$

Entonces: $$\log (i)=\mathrm{Log}(i)+i2\pi k=i\frac{\pi }{2}+i2\pi k=i(\frac{\pi }{2}+2\pi k),k\in \mathbb{Z}.$$

b) Para $z=5$ tenemos que $|z|=5$ y $\mathrm{Arg}(z)=0$, por lo que: $$\mathrm{Log}(5)=\ln (5)+i0=\ln (5).$$

Entonces: $$\log (5)=\mathrm{Log}(5)+i2\pi k=\ln (5)+i2\pi k,k\in \mathbb{Z}.$$

c) Sabemos que para $z=-2$ tenemos que $|z|=-(-2)=2$ y $\mathrm{Arg}(z)=\pi$, por lo que: $$\mathrm{Log}(-2)=\ln (2)+i\pi .$$

Entonces: $$\begin{array}{rl}\log (-2)& =\mathrm{Log}(-2)+i2\pi k\\ & =\ln (2)+i\pi +i2\pi k\\ & =\ln (2)+i(\pi +2\pi k),k\in \mathbb{Z}.\end{array}$$

d) Sea $z=\sqrt{3}+i$, entonces $|z|=\sqrt{4}=2$. Por otra parte: \begin{equation*} \operatorname{Arg}(z) = \operatorname{arctan}\left(\frac{1 {\sqrt{3}}\right) = \frac{\pi}{6}. \end{equation*}

Por lo que: $$\mathrm{Log}(\sqrt{3}+i)=\ln (2)+i\frac{\pi }{6}.$$

Entonces: $$\begin{array}{rl}\log (\sqrt{3}+i)& =\mathrm{Log}(\sqrt{3}+i)+i2\pi k\\ & =\ln (2)+i\frac{\pi }{6}+i2\pi k\\ & =\ln (2)+i(\frac{\pi }{6}+2\pi k),k\in \mathbb{Z}.\end{array}$$

Observación 21.3.
Es interesante notar que si $z\in {\mathbb{R}}^{+}$, es decir es un número real positivo, la rama principal del logaritmo coincide con la función real logaritmo natural. Sin embargo, el logaritmo complejo de un número real positivo tendrá infinitos valores, como vimos en el ejemplo anterior para $z=5$.

Ejemplo 21.2.
Obtengamos todas las soluciones de las siguientes ecuaciones:
a) $e^w=-2i$.
b) $e^w=1+i$.

Solución. Notemos que para cada ecuación, el conjunto de soluciones están dados por el logaritmo complejo, es decir $w=\log (z)$.

a) Sea $z=-2i$. Tenemos que $|z|=\sqrt{(-2{)}^2}=2$ y $\mathrm{Arg}(z)=-\frac{\pi }{2}$, entonces: $$\mathrm{Log}(-2i)=\ln (2)–i\frac{\pi }{2}.$$

Por lo que las soluciones de la ecuación $e^w=-2i$ son: $$\begin{array}{rl}w=\log (-2i)& =\mathrm{Log}(-2i)+i2\pi k\\ & =\ln (2)–i\frac{\pi }{2}+i2\pi k\\ & =\ln (2)+i\left(2\pi k–\frac{\pi }{2}\right),k\in \mathbb{Z}.\end{array}$$

b) Sea $z=1+i$. Tenemos que $|z|=\sqrt{2}$ y: $$\mathrm{Arg}(z)=\arctan (1)=\frac{\pi }{4}$$

Por lo que: $$\mathrm{Log}(1+i)=\ln \left(\sqrt{2}\right)+i\frac{\pi }{4}.$$

Entonces, las soluciones de la ecuación $e^w=1+i$ son: $$\begin{array}{rl}w=\log (1+i)& =\mathrm{Log}(1+i)+i2\pi k\\ & =\ln \left(\sqrt{2}\right)+i\frac{\pi }{4}+i2\pi k\\ & =\ln \left(\sqrt{2}\right)+i(\frac{\pi }{4}+2\pi k),k\in \mathbb{Z}.\end{array}$$

De acuerdo con la definición 13.4 y la observación 15.4, debe ser claro que es posible definir diferentes ramas del logaritmo al elegir diferentes intervalos semiabiertos donde tome valores el argumento. Es decir, si tomamos a un número $\alpha \in \mathbb{R}$ fijo, entonces podemos trabajar con diferentes ramas de la función multivaluada $G(z)=\arg (z)$, definidas sobre $\mathbb{C}\setminus \{0\}$, que tomen valores en intervalos semiabiertos de la forma $I=(\alpha ,\alpha +2\pi ]$ ó $I=[\alpha ,\alpha +2\pi )$ y dadas por ${\mathrm{Arg}}_I(z)\in I$.

Definición 21.3. (Rama $I$ del logaritmo complejo.)
Sean $\alpha \in \mathbb{R}$ fijo, $z\in \mathbb{C}\setminus \{0\}$ e $I$ un intervalo semiabierto de longitud $2\pi$, es decir de la forma $I=(\alpha ,\alpha +2\pi ]$ ó $I=[\alpha ,\alpha +2\pi )$. Definimos a la rama $I$ del logaritmo complejo, denotada por ${\mathrm{Log}}_I(z)$, como: $${\mathrm{Log}}_I(z)=\ln |z|+i{\mathrm{Arg}}_I(z).$$

Observación 21.4.
Al igual que con la rama principal del logaritmo, notemos que una rama $I$ del logaritmo es una función univaluada desde que hemos restringido al argumento de $z\ne 0$ a ser el único argumento tal que $\alpha <\arg z\le \alpha +2\pi$.

Además, a través de la rama $I$ del logaritmo podemos obtener al logaritmo complejo como con la rama principal, observación 21.2, es decir: $$\log (z)={\mathrm{Log}}_I(z)+i2\pi k,k\in \mathbb{Z}.$$

Ejemplo 21.3.
Obtengamos el valor de las siguientes ramas del logartimo.
a) Sea $\alpha =0$. Para $I=[0,2\pi )$ determina ${\mathrm{Log}}_I(-2i)$.
b) Sea $\alpha =\frac{\pi }{2}$. Para $I=(\frac{\pi }{2},\frac{5\pi }{2}]$ determina ${\mathrm{Log}}_I\left(i\right)$.
c) Sea $\alpha =\frac{3\pi }{2}$. Para $I=(\frac{3\pi }{2},\frac{7\pi }{2}]$ determina ${\mathrm{Log}}_I(-2)$.

Solución.
a) Para $I=[0,2\pi )$, recordemos que se obtiene el argumento natural de un número complejo, entrada 13, por lo que si $z=-2i$, entonces: $$|z|=\sqrt{(-2{)}^2}=2,{\mathrm{Arg}}_{[0,2\pi )}(z)=\frac{3\pi }{2}.$$

Por tanto: $${\mathrm{Log}}_{[0,2\pi )}(-2i)=\ln (2)+i\frac{3\pi }{2}.$$

De acuerdo con el ejemplo 21.2(a), notemos que: $${\mathrm{Log}}_{[0,2\pi )}(-2i)\ne \mathrm{Log}(-2i).$$

b) De acuerdo con la proposición 13.3, para $I=(\frac{\pi }{2},\frac{5\pi }{2}]$ y $z=i$ tenemos que $|z|=1$ y: $$\begin{array}{rl}{\mathrm{Arg}}_{(\frac{\pi }{2},\frac{5\pi }{2}]}(z)& =\mathrm{Arg}(-i{e}^{-i\frac{\pi }{2}})+\frac{\pi }{2}+\pi \\ & =\mathrm{Arg}(-i(-i))+\frac{3\pi }{2}\\ & =\mathrm{Arg}(-1)+\frac{3\pi }{2}\\ & =\pi +\frac{3\pi }{2}\\ & =\frac{5\pi }{2}.\end{array}$$

Por lo que: $${\mathrm{Log}}_{(\frac{\pi }{2},\frac{5\pi }{2}]}\left(i\right)=\ln (1)+i\frac{5\pi }{2}=i\frac{5\pi }{2}.$$

De acuerdo con el ejemplo 21.1(a), notemos que: $${\mathrm{Log}}_{(\frac{\pi }{2},\frac{5\pi }{2}]}\left(i\right)\ne \mathrm{Log}(i).$$

c) Sea $I=(\frac{3\pi }{2},\frac{7\pi }{2}]$. Para $z=-2$ tenemos que $|z|=2$ y: $$\begin{array}{rl}{\mathrm{Arg}}_{(\frac{3\pi }{2},\frac{7\pi }{2}]}(z)& =\mathrm{Arg}(-(-2)e^{-i\frac{3\pi }{2}})+\frac{3\pi }{2}+\pi \\ & =\mathrm{Arg}(2(i))+\frac{5\pi }{2}\\ & =\frac{\pi }{2}+\frac{5\pi }{2}\\ & =3\pi .\end{array}$$

Por lo que:
$${\mathrm{Log}}_{(\frac{3\pi }{2},\frac{7\pi }{2}]}(-2)=\ln (2)+i3\pi .$$

De acuerdo con el ejemplo 21.1(c), notemos que: $${\mathrm{Log}}_{(\frac{3\pi }{2},\frac{7\pi }{2}]}(-2)\ne \mathrm{Log}(-2).$$

Proposición 21.1. (Propiedades del logaritmo.)
Para $z_1,z_2,z\in \mathbb{C}\setminus \{0\}$ y $n\in \mathbb{Z}$ se cumple que:

1. $\log (z_1{z}_2)=\log (z_1)+\log (z_2)$.
2. $\log \left({\displaystyle \frac{z_1}{z_2}}\right)=\log (z_1)–\log (z_2)$.
3. $\log \left({\displaystyle \frac{1}{z_1}}\right)=-\log (z_1)$.
4. $\log \left(z^n\right)=n\log (z)$.
5. $e^{\log \left(z\right)}=z$.
6. $\log \left(e^z\right)=z+i2k\pi$, para $k\in \mathbb{Z}$.

Demostración. Sean $z_1,z_2,z\in \mathbb{C}\setminus \{0\}$ y $n\in \mathbb{Z}$.

1. Sabemos que para $r_1,r_2>0$ se cumple que: $$\ln \left(r_1{r}_2\right)=\ln \left(r_1\right)+\ln \left(r_2\right).$$ Por otra parte, por la observación 13.6, sabemos que: $$\arg (z_1{z}_2)=\arg (z_1)+\arg (z_2).$$ De acuerdo con lo anterior tenemos que: $$\begin{array}{rl}\log (z_1{z}_2)& =\ln |z_1{z}_2|+i\arg (z_1{z}_2)\\ & =\ln \left(|z_1||z_2|\right)+i[\arg (z_1)+\arg (z_2)]\\ & =\ln |z_1|+\ln |z_2|+i\arg (z_1)+i\arg (z_2)\\ & =\ln |z_1|+i\arg (z_1)+\ln |z_2|+i\arg (z_2)\\ & =\log (z_1)+\log (z_2).\end{array}$$
2. Se deja como ejercicio al lector.
3. Se deja como ejercicio al lector.
4. Sabemos que para $r>0$ se cumple que: $$\ln \left(r^n\right)=n\ln \left(r\right).$$ Por otra parte, por la observación 13.6, sabemos que para todo $n\in \mathbb{Z}$ se cumple que: $$\arg \left(z^n\right)=n\arg (z).$$ Entonces: $$\begin{array}{rl}\log \left(z^n\right)& =\ln \left|z^n\right|+i\arg \left(z^n\right)\\ & =\ln {\left|z\right|}^n+in\arg (z)\\ & =n\ln \left|z\right|+in\arg (z)\\ & =n[\ln \left|z\right|+i\arg (z)]\\ & =n\log (z).\end{array}$$
5. Sea $z=r{e}^{i\theta }$, con $r=|z|>0$ y $\theta =\arg (z)$, entonces: $$\log (z)=\ln (r)+i\theta ,$$ por lo que: $$e^{\log \left(z\right)}=e^{\ln (r)+i\theta }=e^{\ln (r)}{e}^{i\theta }=r{e}^{i\theta }=z.$$
6. Sea $z=x+iy$, entonces $e^z=e^x{e}^{iy}$, por lo que $|e^z|=e^x$ y $\arg \left(e^z\right)=y+2\pi k$, con $k\in \mathbb{Z}$.
   Entonces: $$\begin{array}{rl}\log \left(e^z\right)& =\ln \left(e^z\right)+i\arg \left(e^z\right)\\ & =\ln \left(e^x\right)+i(y+2\pi k)\\ & =x+iy+i2\pi k\\ & =z+i2\pi k,k\in \mathbb{Z}.\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

En general, las propiedades anteriores no siempre se cumplen para la rama principal del logaritmo.

Ejemplo 21.5.
a) Si $z_1=i$ y $z_2=-1$, entonces $z_1{z}_2=-i$, por lo que: $$\begin{array}{rl}\mathrm{Log}(-i)& =\ln |-i|+i\mathrm{Arg}(-i)\\ & =\ln (1)+i(-\frac{\pi }{2})\\ & =–i\frac{\pi }{2}.\end{array}$$

Por otra parte: $$\begin{array}{rl}\mathrm{Log}(-1)& =\ln |-1|+i\mathrm{Arg}(-1)\\ & =\ln (1)+i\left(\pi \right)\\ & =i\pi .\end{array}$$

Y del ejemplo 21.1(a) sabemos que $\mathrm{Log}(i)=i{\displaystyle \frac{\pi }{2}}$, por lo que:
$$\mathrm{Log}(-i)=–i\frac{\pi }{2}\ne i\frac{3\pi }{2}=\mathrm{Log}(i)+\mathrm{Log}(-1).$$

b) Si $z=-1$, entonces: $$\begin{array}{rl}\mathrm{Log}((-1{)}^{-1})& =\ln |(-1{)}^{-1}|+i\mathrm{Arg}((-1{)}^{-1})\\ & =-\ln (1)+i\left(\pi \right)\\ & =i\pi .\end{array}$$

Mientras que: $$\begin{array}{rl}\mathrm{Log}(-1)& =-\ln |-1|–i\mathrm{Arg}(-1)\\ & =-\ln (1)–i\left(\pi \right)\\ & =-i\pi .\end{array}$$

Entonces: $$\mathrm{Log}((-1{)}^{-1})=i\pi \ne -i\pi =–\mathrm{Log}(-1).$$

Corolario 21.1. (Propiedades de la rama principal del logaritmo.)
Para $z_1,z_2,z\in \mathbb{C}\setminus \{0\}$ y $n\in \mathbb{Z}$ se cumple que:

1. $\mathrm{Log}(z_1{z}_2)=\mathrm{Log}(z_1)+\mathrm{Log}(z_2)+i2\pi N_{+}$,
2. $\mathrm{Log}\left({\displaystyle \frac{z_1}{z_2}}\right)=\mathrm{Log}(z_1)–\mathrm{Log}(z_2)+i2\pi N_{-}$, donde $N_{\pm }$ son números enteros dados por: $$N_{\pm }=\{\begin{array}{lcc}-1& \text{si}& \mathrm{Arg}(z_1)\pm \mathrm{Arg}(z_2)>\pi ,\\ \\ 0& \text{si}& -\pi <\mathrm{Arg}(z_1)\pm \mathrm{Arg}(z_2)\le \pi ,\\ \\ 1& \text{si}& \mathrm{Arg}(z_1)\pm \mathrm{Arg}(z_2)\le -\pi .\end{array}$$
3. $$\mathrm{Log}\left(z^{-1}\right)=\{\begin{array}{lcc}–\mathrm{Log}\left(z\right)& \text{si}& z\in \mathbb{C}\setminus {\mathbb{R}}^{-},\\ \\ -\mathrm{Log}\left(z\right)+i2\pi & \text{si}& z\in {\mathbb{R}}^{-},\end{array}$$ donde ${\mathbb{R}}^{-}=(-\mathrm{\infty },0)$.
4. $$\mathrm{Log}\left(z^n\right)=n\mathrm{Log}\left(z\right)+i2\pi N_n,$$ donde $N_n$ es un número entero dado por: $$N_n=[\frac{1}{2}–\frac{n}{2\pi }\mathrm{Arg}(z)],$$ con $[x]$ la función parte entera de $x$.

Demostración. Se sigue de la proposición 21.1 y la proposición 13.2, por lo que los detalles se dejan como ejercicio al lector.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 21.6.
Considerando el corolario anterior y el ejemplo 21.4 tenemos lo siguiente.
a) Si $z_1=i$ y $z_2=-1$, entonces $\mathrm{Arg}(z_1)=\frac{\pi }{2}$ y $\mathrm{Arg}(z_2)=\pi$, por lo que: $$\mathrm{Arg}(z_1)+\mathrm{Arg}(z_2)=\frac{\pi }{2}+\pi =\frac{3\pi }{2}>\pi .$$

Entonces: $$\mathrm{Log}(z_1{z}_2)=–i\frac{\pi }{2}=i\frac{\pi }{2}+i\pi –i2\pi =\mathrm{Log}(i)+\mathrm{Log}(-1)+i2\pi N_{+}.$$

b) Si $z=-1$, entonces $\mathrm{Arg}(z)=\pi$, por lo que:
$$N_{-1}=[\frac{1}{2}-\left(\frac{-1}{2\pi }\right)\pi ]=\left[1\right]=1.$$

Entonces: $$\mathrm{Log}((-1{)}^{-1})=i\pi =-i\pi +i2\pi (1)=–\mathrm{Log}(-1)+i2\pi N_{-1}.$$

Ejemplo 21.7.
Sean $z_1,z_2,\dots ,z_n\in \mathbb{C}$ tales que $\mathrm{Re}(z_k)>0$ y $\mathrm{Re}(z_1{z}_2\cdots z_k)>0$, para $1\le k\le n$. Veamos que: $$\mathrm{Log}(z_1{z}_2\cdots z_n)=\mathrm{Log}\left(z_1\right)+\cdots +\mathrm{Log}\left(z_n\right).$$ ¿Son necesarias las condiciones dadas?

Solución. Dadas las hipótesis, como $\mathrm{Re}(z_k)>0$ y $\mathrm{Re}(z_1{z}_2\cdots z_k)>0$, para $1\le k\le n$, entonces: $$\mathrm{Arg}(z_k)=\mathrm{arc}\tan \left(\frac{\mathrm{Im}(z_k)}{\mathrm{Re}(z_k)}\right)\in (-\frac{\pi }{2},\frac{\pi }{2}),$$ $$\mathrm{Arg}(b)=\mathrm{arc}\tan \left(\frac{\mathrm{Im}(b)}{\mathrm{Re}(b}\right)\in (-\frac{\pi }{2},\frac{\pi }{2}),$$ con $b=z_1{z}_2\cdots z_k$, para $1\le k\le n$.

Por lo que: $$\mathrm{Log}(z_k)=\ln |z_k|+i\mathrm{Arg}(z_k),$$ $$\mathrm{Log}(z_1{z}_2\cdots z_k)=\ln |z_1{z}_2\cdots z_k|+i\mathrm{Arg}(z_1{z}_2\cdots z_k)$$ para $1\le k\le n$.

Procedemos a realizar la prueba por inducción sobre $n$. Primeramente, consideremos el caso $n=2$. Sean $z_1,z_2\in \mathbb{C}$ bajo las condiciones dadas, entonces: $$-\frac{\pi }{2}<\mathrm{Arg}(z_1)<\frac{\pi }{2},-\frac{\pi }{2}<\mathrm{Arg}(z_1)<\frac{\pi }{2},-\frac{\pi }{2}<\mathrm{Arg}(z_1{z}_2)<\frac{\pi }{2},$$

de donde: $$-\pi <\mathrm{Arg}(z_1)+\mathrm{Arg}(z_2)<\pi ⟹\mathrm{Arg}(z_1{z}_2)=\mathrm{Arg}(z_1)+\mathrm{Arg}(z_2).$$

Entonces:
$$\begin{array}{rl}\mathrm{Log}\left(z_1{z}_2\right)& =\ln \left|z_1{z}_2\right|+i\mathrm{Arg}\left(z_1{z}_2\right)\\ & =\ln \left|z_1\right|+\ln \left|z_2\right|+i\mathrm{Arg}\left(z_1\right)+i\mathrm{Arg}\left(z_2\right)\\ & =\mathrm{Log}\left(z_1\right)+\mathrm{Log}\left(z_2\right).\end{array}$$

Supongamos que el resultado es válido para $n=k-1$. Sean $z_1,\dots ,z_k\in \mathbb{C}$ bajo las condiciones dadas. Entonces: $$\begin{array}{rl}\mathrm{Log}(z_1{z}_2\cdots z_k)& =\mathrm{Log}\left([z_1{z}_2\cdots z_{k-1}]z_k\right)\\ & =\mathrm{Log}(z_1{z}_2\cdots z_{k-1})+\mathrm{Log}\left(z_k\right)\\ & =\mathrm{Log}\left(z_1\right)+\cdots +\mathrm{Log}\left(z_{k-1}\right)+\mathrm{Log}\left(z_k\right).\end{array}$$

Por lo que, el resultado es válido para toda $n\in {\mathbb{N}}^{+}$ tal que los $z_k\in \mathbb{C}$, con $1\le k\le n$, cumplen las condiciones dadas.

Por último veamos que las condiciones dadas son necesarias para que se cumpla el resultado.

Supongamos que no es necesaria la condición $\mathrm{Re}(z_k)>0$, para $1\le k\le n$. Sean $z_1=z_2=e^{i\frac{2\pi }{3}}$, entonces: $$\mathrm{Arg}(z_1)=\mathrm{Arg}(z_2)=\mathrm{arc}\tan (-\sqrt{3})+\pi =\frac{2\pi }{3}.$$

Pero: $$\mathrm{Arg}(z_1{z}_2)=\mathrm{arc}\tan \left(\sqrt{3}\right)–\pi =–\frac{2\pi }{3}.$$

Por lo que: $$\mathrm{Arg}(z_1{z}_2)\ne \mathrm{Arg}(z_1)+\mathrm{Arg}(z_2),$$ entonces $\mathrm{Log}(z_1{z}_2)\ne \mathrm{Log}(z_1)+\mathrm{Log}(z_2)$.

Supongamos ahora que la condición $\mathrm{Re}(z_1{z}_2\cdots z_k)>0$, para $1\le k\le n$, no es necesaria.

Sean $z_1=\cdots =z_9=e^{i\frac{\pi }{4}}$, entonces: $$\mathrm{Arg}(z_1\cdots z_9)=\mathrm{arc}\tan \left(1\right)=\frac{\pi }{4},$$

pero: $$\mathrm{Arg}(z_1)=\cdots =\mathrm{Arg}(z_9)=\frac{\pi }{4},$$

es decir: $$\mathrm{Arg}(z_1)+\cdots +\mathrm{Arg}(z_9)=\frac{9\pi }{4}.$$

Por lo que: $$\mathrm{Arg}(z_1\cdots z_9)\ne \mathrm{Arg}(z_1)+\cdots +\mathrm{Arg}(z_9),$$

entonces: $$\mathrm{Log}(z_1\cdots z_9)\ne \mathrm{Log}(z_1)+\cdots +\mathrm{Log}(z_9).$$

En este caso la igualdad no se cumple desde que $\mathrm{Re}(z_1{z}_2{z}_3)<0$.

Proposición 21.2. (Continuidad de la rama principal del logaritmo.)
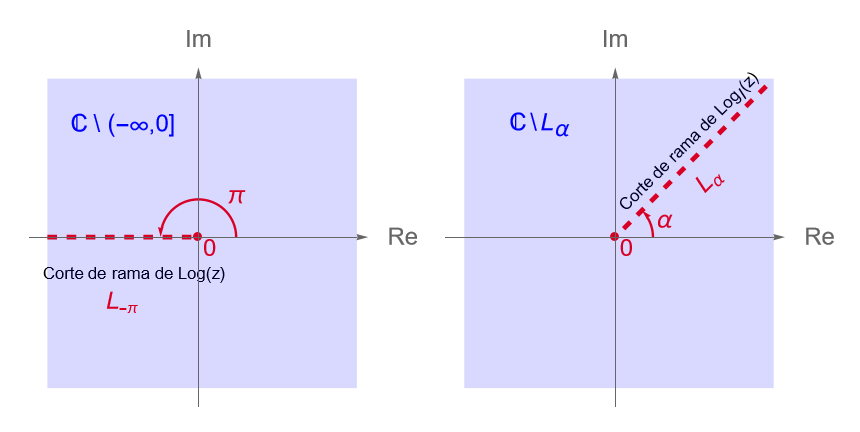
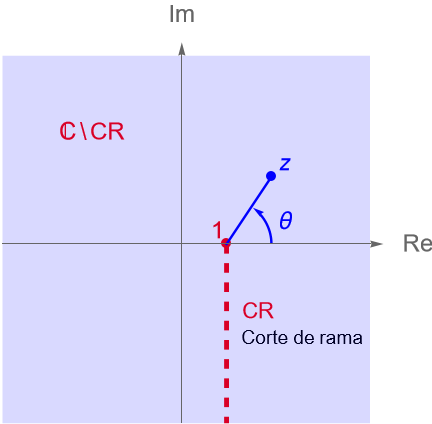
Sea $D=\mathbb{C}\setminus (-\mathrm{\infty },0]$. La rama principal del logaritmo complejo, $f(z)=\mathrm{Log}(z)$, es una función continua para todo $z\in D$. Para $z\in (-\mathrm{\infty },0]$, las discontinuidades de $\mathrm{Log}(z)$ son irremovibles.

Demostración. Tenemos que la rama principal del logaritmo es: $$f(z)=\mathrm{Log}(z)=\ln |z|+i\mathrm{Arg}(z),z\ne 0.$$

Es claro que dicha función está dada por la suma de dos funciones, por lo que el dominio donde $f$ es continua dependerá de la continuidad de cada una de las funciones que la conforman.

Primeramente, sabemos que la función $|z|$ determina una función real de variable compleja, la cual es continua para todo $z\in \mathbb{C}$, mientras que la función real logaritmo natural es continua para todo $x>0$, por lo que la composición $\ln |z|$ será continua para todo $z\ne 0$.

Por otra parte, de acuerdo con el ejemplo 15.5, sabemos que la función $\mathrm{Arg}(z)$ es continua para todo $z\in \mathbb{C}\setminus (-\mathrm{\infty },0]$. Además, los $z\in (-\mathrm{\infty },0]$ son discontinuidades irremovibles, por lo que también serán discontinuidades irremovibles de la función $\mathrm{Log}(z)$.

Por lo tanto, $f(z)=\mathrm{Log}(z)$ es una función continua en $\mathbb{C}\setminus (-\mathrm{\infty },0]$, es decir es una rama de la función multivaluada $F(z)=\log (z)$.

Observación 21.5.
Notemos que: $$L_{-\pi }=\{r{e}^{-i\pi }:r\ge 0\}=\{-r:r\ge 0\}=(-\mathrm{\infty },0],$$ es decir que dicha semirrecta representa el corte de rama de la función $\mathrm{Log}(z)$, figura 79.

Observación 21.6.
En general, las ramas definidas en 21.3 serán ramas de la función multivaluada $F(z)=\log (z)$ en el sentido estricto, es decir de acuerdo con la definición 13.2, siempre que se restringa su dominio al conjunto $\mathbb{C}\setminus L_{\alpha }$, con $L_{\alpha }=\{r{e}^{i\alpha }:r\ge 0\}$, pues como vimos en la observación 15.4 la función ${\mathrm{Arg}}_I(z)$ es discontinua en la semirrecta $L_{\alpha }$ que parte desde el origen y forma un ángulo $\alpha$ con respecto al eje real positivo. Dicha semirrecta corresponde con el corte de rama de la función ${\mathrm{Log}}_I(z)$, figura 79.

Podemos generalizar lo anterior mediante la siguiente:

Definición 21.4. (Rama del logaritmo.)
Si $D\subset \mathbb{C}\setminus \{0\}$ es un dominio y $f:D\to \mathbb{C}$ es una función continua tal que $e^{f(z)}=z$ para todo $z\in D$, entonces diremos que $f$ es una rama del logaritmo en $D$.

Recordemos que definimos al logaritmo complejo como la solución a la ecuación $e^w=z$, es decir como «la inversa» de la exponencial. Sin embargo, de acuerdo con la proposición 21.1(6), sabemos que en general $\log \left(e^z\right)=z+i2\pi k$, para algún $k\in \mathbb{Z}$. Este hecho nos lleva a preguntarnos bajo qué restricciones se cumple que $\log \left(e^z\right)=z$.

Proposición 21.3. (Inversa de la función exponencial compleja.)
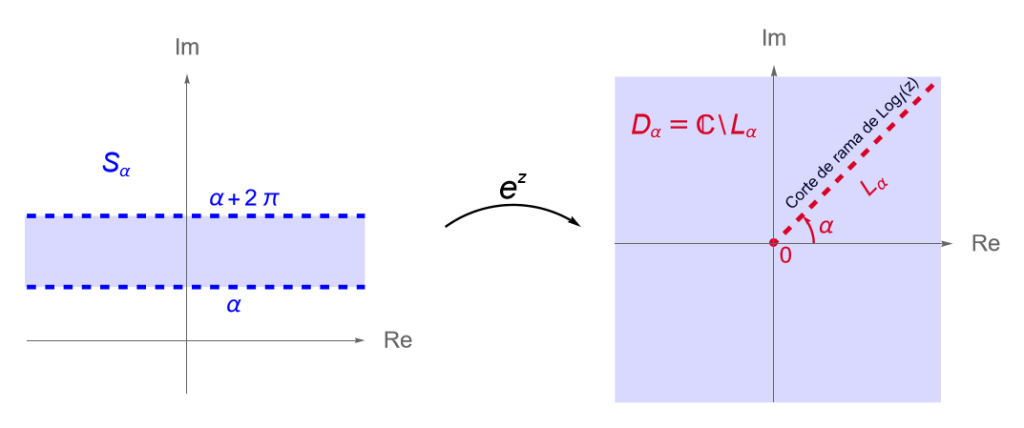
Sea $\alpha \in \mathbb{R}$ fijo. Definimos a la banda abierta: $$S_{\alpha }=\{z=x+iy\in \mathbb{C}:x\in \mathbb{R},\alpha <y<\alpha +2\pi \},$$ y al plano complejo cortado: $$D_{\alpha }=\mathbb{C}\setminus L_{\alpha }=\{w\in \mathbb{C}:|w|>0,\alpha <\arg (w)<\alpha +2\pi \},$$ donde $L_{\alpha }=\{r{e}^{i\alpha }:r\ge 0\}$.

Entonces, la función $f:S_{\alpha }\to D_{\alpha }$, dada por $f(z)=e^z$, es biyectiva.

Demostración. Sea $\alpha \in \mathbb{R}$ fijo. Primero probemos la inyectividad.

Sean $z_1=x_1+i{y}_1,z_2=x_2+i{y}_2\in S_{\alpha }$ y supongamos que $e^{z_1}=e^{z_2}$, entonces: $$|e^{z_1}|=|e^{z_2}|,\arg \left(e^{z_1}\right)=\arg \left(e^{z_2}\right).$$

Por lo que $e^{x_1}=e^{x_2}$ y $y_2=y_1+2\pi n$, con $n\in \mathbb{Z}$. Dado que $z_1,z_2\in S_{\alpha }$, tenemos que $x_1,x_2\in \mathbb{R}$ y $y_1,y_2\in (\alpha ,\alpha +2\pi )$. Entonces $x_1=x_2$ y: $$-2\pi <y_2–y_1<2\pi ⟺-2\pi <2n\pi <2\pi ⟺n=0,$$ por lo que $y_1=y_2$, es decir $z_1=z_2$.

Verifiquemos ahora la supreyectividad. Sea $w=r{e}^{i\theta }\in D_{\alpha }$, con $r=|w|>0$ y $\theta ={\mathrm{Arg}}_I(w)\in I$, donde $I=(\alpha ,\alpha +2\pi )$. Definimos: $$z=\ln (r)+i\theta .$$

Claramente $z\in S_{\alpha }$ y $e^z=e^{\ln (r)+i\theta }=e^{\ln (r)}{e}^{i\theta }=r{e}^{i\theta }=w$.

Por lo tanto, $f(z)=e^z$ biyecta la banda abierta $S_{\alpha }$ en el plano complejo cortado $D_{\alpha }$, figura 80.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 21.7.
En la entrada 26 veremos que al considerar a las funciones $f(z)=e^z$ y $g(z)=\mathrm{Log}(z)$ como mapeos, es posible verificar geométricamente las transformaciones del plano complejo dadas en la figura 80.

Observación 21.8.
Dado que una rama del logaritmo, definida sobre el plano complejo cortado $D_{\alpha }$, corresponde con una rama de la función multivaluada $F(z)=\log (z)$, definición 13.2, entonces se sigue del resultado anterior que cualquier rama del logaritmo, bajo dicha restricción, será una inversa de la función exponencial compleja.

Este hecho resulta de suma importancia pues nos dice que la inversa de la función exponencial compleja no es única y que habrá tantas inversas como ramas del logaritmo complejo.

Corolario 21.2. (La rama principal del logaritmo es una inversa de la función exponencial.)
La función exponencial compleja, $f(z)=e^z$, definida en la región fundamental:
$$S_{-\pi }=\{z=x+iy\in \mathbb{C}:x\in \mathbb{R},-\pi <y<\pi \},$$ con valores en el plano complejo cortado $D_{-\pi }=\mathbb{C}\setminus (-\mathrm{\infty },0]$, es biyectiva y su inversa es la rama principal del logaritmo.

Demostración. La primera parte del resultado se sigue de la proposición anterior, por lo que solo resta ver que en efecto la rama principal del logaritmo es la inversa de la función exponencial, bajo estas restricciones.

Por la proposición 21.1 es claro que $e^{\mathrm{Log}(z)}=z$. Veamos que $\mathrm{Log}\left(e^z\right)=z$.

Sea $z=x+iy\in S_{-\pi }$, entonces $x\in \mathbb{R}$ y $-\pi <y<\pi$. Tenemos que $e^z=e^x{e}^{iy}$, por lo que $\left|e^z\right|=e^x$ y $\mathrm{Arg}\left(e^z\right)=y$. Entonces: $$\mathrm{Log}\left(e^z\right)=\ln \left(e^x\right)+i\mathrm{Arg}\left(e^z\right)=x+iy=z.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 21.4. (Analicidad de la rama principal del logaritmo.)
La rama principal del logaritmo $g(z)=\mathrm{Log}(z)$ es analítica en $D_{-\pi }=\mathbb{C}\setminus (-\mathrm{\infty },0]$ y su derivada es: $$\frac{d}{dz}\mathrm{Log}(z)=\frac{1}{z},\mathrm{\forall }z\in D_{-\pi }.$$

Demostración. Del corolario 21.2 se sigue que la función $f:S_{-\pi }\to D_{-\pi }$ dada por $f(z)=e^z$ es biyectiva y su inversa es la función $g:D_{-\pi }\to S_{-\pi }$ dada por $g(z)=\mathrm{Log}(z)$, la cual es continua en $D_{-\pi }$ (proposición 21.2).

Por la proposición 20.1 sabemos que la función $f(z)=e^z$ es entera y que su derivada es $f^{\prime }(z)=e^z$. Más aún, sabemos por la proposición 20.2(4) que $e^z\ne 0$ para todo $z\in \mathbb{C}$. Por lo que $f$ es una función analítica en $S_{-\pi }$ tal que $f^{\prime }(g(z))\ne 0$ para todo $z\in D_{-\pi }$, con $g$ continua en dicho dominio.

Entonces, por el teorema de la función inversa (proposición 16.6), se sigue que $g$ es analítica en $D_{-\pi }$ y su derivada es: $$g^{\prime }(z)=\frac{1}{f^{\prime }(g(z))}=\frac{1}{e^{\mathrm{Log}(z)}}=\frac{1}{z},\mathrm{\forall }z\in D_{-\pi }.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 21.5. (Analicidad de una rama $I$ del logaritmo.)
Sean $\alpha \in \mathbb{R}$ fijo e $I=(\alpha ,\alpha +2\pi )$. La rama ${\mathrm{Log}}_I:D_{\alpha }\to S_{\alpha }$ dada por: $$\mathrm{Log}I(z)=\ln |z|+i{\mathrm{Arg}}_I(z),$$ es una función analítica en $D_{\alpha }$ y su derivada es: $$\frac{d}{dz}{\mathrm{Log}}_I(z)=\frac{1}{z},\mathrm{\forall }z\in D_{\alpha }.$$

Demostración. Su prueba es análoga a la de la proposición 21.3, por lo que se deja como ejercicio al lector.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

De manera general tenemos que:

Proposición 21.6.
Sean $D\subset \mathbb{C}\setminus \{0\}$ un dominio y $L:D\to \mathbb{C}$ una rama del logaritmo en $D$. Entonces $L$ es analítica en $D$ y $L^{\prime }(z)=1/z$ para todo $z\in D$.

Demostración. Dadas las hipótesis, como $L$ es una rama del logaritmo en $D$, entonces por la definición 21.4 tenemos que: $$e^{L(z)}=z,\mathrm{\forall }z\in D.$$

Dado que la función $f(z)=e^z$ es entera y $f^{\prime }(z)=e^z\ne 0$ para todo $z\in \mathbb{C}$, entonces si restringimos $f:L(D)\to \mathbb{C}$, es claro que $f$ y $L$ serán inversas, por lo que se sigue del teorema de la función inversa (proposición 16.6) que $L$ es analítica en $D$ y su derivada está dada por: $$L^{\prime }(z)=\frac{1}{f^{\prime }(L(z))}=\frac{1}{e^{L(z)}}=\frac{1}{z},\mathrm{\forall }z\in D.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 21.8.
Estudiemos la analicidad de las siguientes funciones y obtengamos su derivada.
a) $f(z)=\mathrm{Log}(z-i)$.
b) $f(z)={\displaystyle \frac{\mathrm{Log}(z+4)}{z^2+i}}$.

Solución.
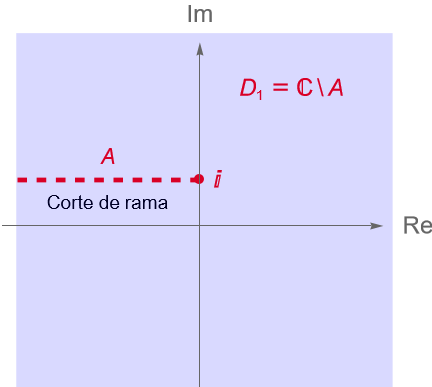
a) Sabemos que la función $g(w)=\mathrm{Log}(w)$ es analítica en el dominio $D=\mathbb{C}\setminus (-\mathrm{\infty },0]$. Procedemos a determinar el corte de rama de $f$. Sea $w=z–i$, con $z=x+iy\in \mathbb{C}$, entonces: $$w\in (-\mathrm{\infty },0]=L_{-\pi }=\{-r\in \mathbb{C}:r\ge 0\}⟺w\in \{w\in \mathbb{C}:\mathrm{Re}(w)\le 0,\mathrm{Im}(w)=0\}.$$

Por lo que, el corte de rama de $f$ está dado por las condiciones: $$\{\begin{array}{l}\mathrm{Re}(z-i)=x\le 0,\\ \\ \mathrm{Im}(z-i)=y-1=0,\end{array}⟹\{\begin{array}{l}x\le 0,\\ \\ y=1.\end{array}$$

Es decir, el corte de rama de $f$ es el conjunto: $$A=\{z=x+iy\in \mathbb{C}:x\le 0,y=1\}.$$

Entonces, $f$ es analítica en el dominio $D_1=\mathbb{C}\setminus A$, figura 81(a).

Dado que $f=g\circ h$, con $g(z)=\mathrm{Log}(z)$ y $h(z)=z-i$, entonces por la regla de la cadena tenemos que: $$\frac{d}{dz}\mathrm{Log}(z-i)=g^{\prime }(h(z))h^{\prime }(z)=\frac{1}{z-i},\mathrm{\forall }z\in D_1.$$

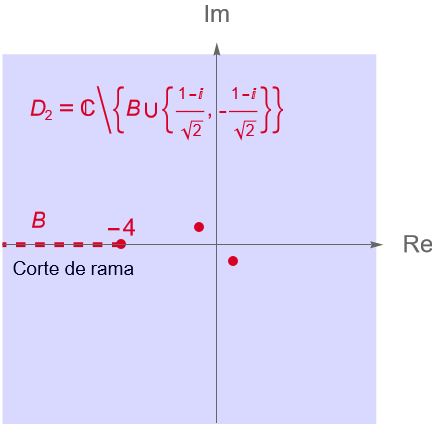
b) Dado que $f$ es una función racional, es claro que los puntos donde el denominador se anule no serán elementos del dominio de analicidad de $f$. Tenemos que: $$z^2+i=0⟺z=\pm \sqrt{1}{e}^{-i\frac{\pi }{4}}=\pm \frac{\sqrt{2}}{2}(1-i).$$

Por otra parte, procediendo como en el inciso anterior, para $w=z+4$, con $z=x+iy\in \mathbb{C}$, tenemos que las condiciones que determinan el corte de rama de $f$ son: $$\{\begin{array}{l}\mathrm{Re}(z+4)=x+4\le 0,\\ \\ \mathrm{Im}(z+4)=y=0,\end{array}⟹\{\begin{array}{l}x\le -4,\\ \\ y=0.\end{array}$$

De donde se sigue que el corte de rama de $f$ es el conjunto: $$B=\{z=x+iy\in \mathbb{C}:x\le -4,y=0\}.$$

Por lo que, al tener los puntos donde $f$ no está definida y el corte de rama del númerador, concluimos que $f$ es analítica en el dominio, figura 81(b): $$D_2=\mathbb{C}\setminus \{B\cup \{\frac{\sqrt{2}}{2}(1-i),\frac{\sqrt{2}}{2}(i-1)\}\}.$$

Procedemos a obtener la derivada de $f$ utilizando las reglas de derivación y la regla de la cadena, entonces: $$\begin{array}{rl}\frac{d}{dz}f(z)& =\frac{[\frac{d}{dz}\mathrm{Log}(z+4)]–[\frac{d}{dz}(z^2+i)]\mathrm{Log}(z+4)}{(z^2+i{)}^2}\\ & =\frac{\left[\frac{1}{z+4}\right]-\left[2z\right]\mathrm{Log}(z+4)}{(z^2+i{)}^2}\\ & =\frac{z^2+i-2z(z+4)\mathrm{Log}(z+4)}{(z^2+i{)}^2(z+4)},\mathrm{\forall }z\in D_2.\end{array}$$

Figura 81: Dominios de analicidad de las funciones del ejemplo 21.8.

Proposición 21.7.
Sean $D\subset \mathbb{C}\setminus \{0\}$ un dominio y $f:D\to \mathbb{C}$ una función analítica. Entonces $f$ es una rama del logaritmo si y solo si $f^{\prime }(z)=1/z$ para todo $z\in D$ y $e^{f(a)}=a$ para al menos un $a\in D$.

Demostración. Dadas las hipótesis.

$\Rightarrow )$

Supongamos que $f$ es una rama del logaritmo, entonces por definición: $$e^{f(z)}=z,\mathrm{\forall }z\in D.$$

Claramente $e^{f(a)}=a$ para al menos un $a\in D$.

Por otra parte, dado que $f$ es analítica en $D$, tenemos que la función $e^{f(z)}$ es analítica en $D$, entonces derivando de ambos lados de la igualdad, por la regla de la cadena, tenemos que: $$e^{f(z)}\cdot f^{\prime }(z)=1\Rightarrow f^{\prime }(z)=\frac{1}{e^{f(z)}},$$

por lo que: $$f^{\prime }(z)=\frac{1}{z},\mathrm{\forall }z\in D.$$

$(\Leftarrow$

Supongamos que $f^{\prime }(z)=1/z$ para todo $z\in D$ y que existe $a\in D$ tal que $e^{f(a)}=a$. Veamos que $f$ es una rama del logaritmo.

Definimos a la función $g(z)=z\cdot e^{-f(z)}$. Claramente $g$ es una función analítica en $D$ y por tanto diferenciable. Entonces para todo $z\in D$ se cumple que: $$\begin{array}{rl}{g}^{\prime }(z)& =\frac{d}{dz}\left(z{e}^{-f(z)}\right)\\ & =e^{-f(z)}{\displaystyle \frac{dz}{dz}}+z\frac{d}{dz}\left(e^{-f(z)}\right)\\ & =e^{-f(z)}–z{e}^{-f(z)}{f}^{\prime }(z)\\ & =e^{-f(z)}–z{e}^{-f(z)}\left(\frac{1}{z}\right)\\ & =e^{-f(z)}–e^{-f(z)}\\ & =0,\end{array}$$ por lo que $g$ es una función constante, es decir: $$g(z)=k,k\in \mathbb{C}.$$

Procedemos a determinar el valor de dicha constante. Sea $z=a$, entonces: $$g(a)=a\cdot e^{-f(a)}=k.$$

Dado que $e^{f(a)}=a$, tenemos que: $$e^{-f(a)}=\frac{1}{a},$$

por lo tanto: $$k=a\cdot e^{-f(a)}=a\left(\frac{1}{a}\right)=1.$$

Se sigue que $g(z)=1$, es decir: \begin{equation} z \cdot e^{-f(z)} = 1, \end{equation*} de donde: $$e^{f(z)}=z,\mathrm{\forall }z\in D,$$ por lo que $f$ es una rama del logaritmo.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 21.8.
Sean $D\subset \mathbb{C}\setminus \{0\}$ un dominio y $L:D\to \mathbb{C}$ una rama del logaritmo en $D$. Entonces, todas las ramas del logaritmo en $D$ son de la forma:
$$\begin{array}{}\text{(21.1)}& l(z)=L(z)+i2\pi k,k\in \mathbb{Z}.\end{array}$$

Demostración. Dadas las hipótesis, primeramente notemos que para $k\in \mathbb{Z}$ la función $l(z)$ dada en (21.1) es continua en $D$ y: $$e^{l(z)}=e^{L(z)+i2\pi k}=e^{L(z)}{e}^{i2\pi k}=e^{L(z)}=z,$$ es decir que $l(z)$ define otra rama del logaritmo en $D$.

Supongamos que $l:D\to \mathbb{C}$ es otra rama del logaritmo en $D$, distinta de $L$. Entonces para todo $z\in D$ tenemos que: $$e^{L(z)–l(z)}=\frac{e^{L(z)}}{e^{l(z)}}=\frac{z}{z}=1.$$

De acuerdo con la proposición 20.2(10), lo anterior implica que $L(z)–l(z)=i2k\pi$, para algún $k\in \mathbb{Z}$. Notemos que el mismo $k\in \mathbb{Z}$ funciona para todo $z\in D$, ya que si definimos a la función: $$k(z)=\frac{L(z)–l(z)}{i2\pi },$$ es claro que $k(z)$ es una función continua en $D$ y su imagen es un subconjunto de $\mathbb{Z}$. Dado que $D$ es conexo y $k(z)$ es continua, entonces por la proposición 10.3 tenemos que $k(D)$ es un conjunto conexo, por lo que $k(D)=\left\{k\right\}$ para un único $k\in \mathbb{Z}$ tal que $l(z)=L(z)+i2k\pi$ para todo $z\in D$. Es decir, dos ramas del logaritmo en $D$ difieren a lo más en un múltiplo entero de $2\pi i$, por lo que su diferencia es constante, de donde se sigue el resultado.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 21.9.
Determinemos los puntos de ramificación de la función multivaluada $F(z)=\log (z^2-1)$.

Solución. Primeramente notemos que la función multivaluada: $$G(w)=\log (w)=\ln |w|+i\arg (w),$$ no está definida para $w=0$, por lo que tiene sentido que dicho punto sea un punto de ramificación de $G$, lo cual es claro desde que $w=0$ es un punto de ramificación de la función multivaluada $\arg (w)$, pues siempre que un punto arbitrario de una vuelta completa alrededor de dicho punto, su argumento habrá aumentado en $2\pi$ y por tanto habrá cambiado de rama del argumento.

Notemos que: $$\begin{array}{rl}F(z)& =\log (z^2-1)\\ & =\log ((z-1)(z+1))\\ & =\log (z-1)+\log (z+1).\end{array}$$

Entonces, considerando lo anterior, tenemos que los posibles puntos de ramificación son $z=1$ y $z=-1$.

Sean: $$\begin{array}{r}z-1=r_1{e}^{i{\theta }_1},r_1=|z-1|,{\theta }_1=\arg (z-1),\\ z+1=r_2{e}^{i{\theta }_2},r_2=|z+1|,{\theta }_2=\arg (z+1),\end{array}$$

entonces: $$F(z)=\ln (r_1)+\ln (r_2)+i({\theta }_1+{\theta }_2).$$

Procediendo como en el ejemplo 13.15, si tomamos un punto $z_0$ sobre una circunferencia con centro en el punto $z=1$ y de radio lo suficientemente pequeño como para que el punto $z=-1$ sea exterior a ella, entonces tenemos que: $$F(z_0)=\ln (r_1)+\ln (r_2)+i({\theta }_1+{\theta }_2).$$

Si el punto $z_0$ da una vuelta alrededor de $z=1$, entonces solo el argumento de $z_0-1$ se verá modificado, es decir: $$F(z_0)=\ln (r_1)+\ln (r_2)+i({\theta }_1++2\pi +{\theta }_2),$$ por lo que $F$ cambio de rama. Entonces $z=1$ es un punto de ramificación de $F$.

De manera análoga podemos concluir que $z=-1$ también es un punto de ramificación de $F$.

A diferencia del ejemplo 13.15, en este caso el punto $z_{\mathrm{\infty }}=\mathrm{\infty }$ sí será un punto de ramificación de $F$.

Tenemos que: $$\begin{array}{rl}F\left(\frac{1}{z}\right)& =\log (\frac{1}{z^2}-1)\\ & =\log \left(\frac{1–z^2}{z^2}\right)\\ & =\log (1-z^2)–\log (z^2)\\ & =\log (1-z^2)–2\log (z).\end{array}$$

Entonces, es claro que $z=0$ es un punto de ramificación de $F(1/z)$, por lo que $z_{\mathrm{\infty }}=\mathrm{\infty }$ será también un punto de ramificación de $F(z)$.

Al igual que en el caso real, podemos utilizar a las funciones complejas exponencial y logaritmo para definir a las potencias complejas. Recordemos que para todo $a>0$ y $b\in \mathbb{R}$, definimos a la potencia real de base $a$ y exponente $b$ como $a^b=e^{b\ln (a)}$.

Sabemos que para todo $z\ne 0$ se cumple que: $$z=e^{\log (z)},$$ pero como la función $\log (z)$ es multivaluada, entonces existen infinitos logaritmos de $z$, tantos como múltiplos enteros de $i2\pi$, pues: $$\log (z)=\mathrm{Log}(z)+i2\pi k,k\in \mathbb{Z}.$$

Considerando lo anterior, tenemos la siguiente:

Definición 21.5. (Potencias complejas.)
Sean $a\in \mathbb{C}$ y $z\in \mathbb{C}\setminus \{0\}$. Definimos a la potencia compleja, de base $z$ y exponente $a$, como: $$z^a=e^{a\log (z)}.$$

Observación 21.9.
En general, la potencia compleja de $z\ne 0$ define a una función multivaluada, por lo que, al elegir una rama del logaritmo complejo obtendremos una función univaluada a la cual llamaremos rama de la potencia compleja. En particular, si elegimos a la rama principal del logaritmo entonces obtendremos el valor principal o la rama principal de $z^a$, es decir: $$z^a=e^{a\mathrm{Log}(z)}.$$

Por otra parte, si elegimos a una rama $I$ del logaritmo, entonces obtenemos la rama $I$ de $z^a$, es decir: $$z^a=e^{a{\mathrm{Log}}_I(z)}.$$

Recordemos que para hablar de ramas de una función multivaluada debemos tener funciones continuas, por lo que, de acuerdo con los resultados previos, bastará con tomar intervalos abiertos $I$ de longitud $2\pi$, es decir de la forma $I=(\alpha ,\alpha +2\pi )$, con $\alpha \in \mathbb{R}$ fijo, para garantizar que la rama del logaritmo elegida sea en efecto continua.

Ejemplo 21.10.
Determinar todos los valores de las siguientes potencias complejas.
a) $1^i$.
b) $(-2{)}^i$.
c) $i^{-2i}$.

Solución.
a) Dado que $|1|=1$ y $\mathrm{Arg}(1)=0$, entonces: $$\begin{array}{rl}\mathrm{Log}(1)& =\ln (1)+i\mathrm{Arg}(1)\\ & =0+i0\\ & =0,\end{array}$$ de donde $\log (1)=\mathrm{Log}(1)+i2\pi k=i2\pi k$, con $k\in \mathbb{Z}$. Entonces: $$1^i=e^{i\log (1)}=e^{-2\pi k},k\in \mathbb{Z}.$$

b) De acuerdo con el ejercicio 21.1(c) sabemos que $\log (-2)=\ln (2)+i(\pi +2\pi k)$, con $k\in \mathbb{Z}$. Entonces: $$(-2{)}^i=e^{i\log (-2)}=e^{i\ln (2)}{e}^{-(\pi +2\pi k)},k\in \mathbb{Z}.$$

c) Por el ejercicio 21.1(a) sabemos que $\log (i)=i(\frac{\pi }{2}+2\pi k)$, con $k\in \mathbb{Z}$. Entonces: $$i^{-2i}=e^{-2i\log (i)}=e^{2(\frac{\pi }{2}+2\pi k)}=e^{(4k+1)\pi },k\in \mathbb{Z}.$$

Es interesante notar que las potencias complejas no siempre devuelven valores complejos, como es el caso de los incisos a) y c) del ejemplo anterior, cuyos valores son siempre números reales.

Ejemplo 21.11.
Para $z=-i$ y $a=1+i$, calculemos las siguientes potencias complejas.
a) Si $I=(-\pi ,\pi )$, determinar el valor de $z^a$.
b) Si $I=(0,2\pi )$, determinar el valor de $z^a$.
c) Determinar todos los valores de $z^a$.

Solución.
a) Si $I=(-\pi ,\pi )$, entonces estamos considerando a la rama principal del logaritmo. Para $z=-i$ y $a=1+i$, tenemos que $|z|=1$ y $\mathrm{Arg}(z)=-\frac{\pi }{2}$, por lo que: $$\mathrm{Log}(-i)=\ln (1)+i(-\frac{\pi }{2})=-i\frac{\pi }{2}.$$

Entonces: $$\begin{array}{rl}(-i{)}^{1+i}& =e^{(1+i)\mathrm{Log}(-i)}\\ & =e^{(1+i)(-i\frac{\pi }{2})}\\ & =e^{-i\frac{\pi }{2}}{e}^{\frac{\pi }{2}}\\ & =-i{e}^{\frac{\pi }{2}}.\end{array}$$

b) Si $I=(0,2\pi )$, entonces estamos considerando la rama natural del argumento, por lo que para $z=-i$ tenemos que ${\mathrm{Arg}}_{(0,2\pi )}(z)=\frac{3\pi }{2}$. Entonces: $${\mathrm{Log}}_I(-i)=\ln (1)+i\left(\frac{3\pi }{2}\right)=i\frac{3\pi }{2}.$$

Por lo que: $$\begin{array}{rl}(-i{)}^{1+i}& =e^{(1+i){\mathrm{Log}}_I(-i)}\\ & =e^{(1+i)\left(i\frac{3\pi }{2}\right)}\\ & =e^{i\frac{3\pi }{2}}{e}^{-\frac{3\pi }{2}}\\ & =-i{e}^{-\frac{3\pi }{2}}.\end{array}$$

Claramente $-i{e}^{-\frac{3\pi }{2}}\ne -i{e}^{\frac{\pi }{2}}$, por lo que el valor de $(-i{)}^{1+i}$ es distinto al considerar estas dos ramas del logaritmo.

c) De acuerdo con el inciso a) tenemos que: $$\log (-i)=\mathrm{Log}(-i)+i2\pi k=i\frac{\pi }{2}(4k-1),k\in \mathbb{Z}.$$

Entonces: $$(-i{)}^{1+i}=e^{(1+i)\log (-i)}=e^{i\frac{\pi }{2}(4k-1)}{e}^{-\frac{\pi }{2}(4k-1)},k\in \mathbb{Z}.$$

En particular si $k=1$ obtenemos la rama del inciso b) y si $k=0$ obtenemos la rama del inciso a).

En la observación 21.8 hemos mencionado que en general la función $z^a$, con $z\ne 0$, corresponde con una función multivaluada, por lo que podemos preguntarnos bajo qué condiciones no lo es. Para responder esta pregunta notemos que para $z\ne 0$ y $a\in \mathbb{C}$ se cumple que: $$z^a=e^{a\log (z)}=e^{a(\mathrm{Log}(z)+i2\pi k)}=e^{a\mathrm{Log}(z)}{e}^{i2a\pi k},k\in \mathbb{Z}.$$

Por lo que, para determinar el número de valores distintos que toma $z^a$ basta con determinar el número de valores distintos que toma $e^{i2a\pi k}$, con $k\in \mathbb{Z}$. Planteamos los siguientes casos:

1. Si $a\in \mathbb{Z}$. Si $a$ es un entero tenemos que la expresión $i2a\pi k$ determina un múltiplo entero de $i2\pi$. Entonces, por la proposición 20.2(10), se tiene que $e^{i2a\pi k}=1$ para todo $k\in \mathbb{Z}$, de donde se concluye que $z^a$ determina un único valor, es decir es una función univaluada, lo cual es concordante con las funciones de la forma $z^n$, con $n\in \mathbb{Z}$, es decir las potencias enteras.
2. Si $a\in \mathbb{Q}$. Si $a$ es un número real racional entonces se puede escribir de la forma $a=\frac{p}{q}$, con $p,q\in \mathbb{Z}$, $q\ne 0$, coprimos. Por lo que, la expresión $e^{i2a\pi k}=e^{i2\pi \frac{pk}{q}}$ tendrá exactamente $q$ valores distintos para $k=0,1,\dots ,q-1$ (observación 5.4, entrada 5). Entonces, para cada valor de $k\in \{0,1,\dots ,q-1\}$ obtendremos una potencia compleja distinta, es decir una función de la forma: $$z^{\frac{p}{q}}=e^{\frac{p}{q}\mathrm{Log}(z)}{e}^{i2\pi \frac{pk}{q}},$$ correspondiente con una rama de la función $z^{\frac{p}{q}}$. En particular, para $k=0$ obtendremos la rama principal de la función multivaluada $z^{\frac{p}{q}}$. Es claro que el caso 1 es un caso particular del caso 2 tomando $q=1$.
3. Si $a\in \mathbb{R}\setminus \mathbb{Q}$ ó $a\in \mathbb{C}\setminus \mathbb{R}$. En este caso tenemos que $a$ puede ser un número real irracional o un número complejo cuya parte imaginaria es distinta de cero. Veamos que en cualquiera de estos casos los valores de la expresión $e^{i2a\pi k}$ serán distintos para todo $k\in \mathbb{Z}$.
   Supongamos que $a\in \mathbb{R}\setminus \mathbb{Q}$ y que: $$\begin{array}{}\text{(21.2)}& e^{i2a\pi k}=e^{i2a\pi j},k,j\in \mathbb{Z},\end{array}$$ entonces: $$e^{i2a\pi k–i2a\pi j}=e^{i2a\pi (k-j)}=1,k,j\in \mathbb{Z},$$ pero lo anterior se cumple si y solo si $a(k-j)\in \mathbb{Z}$, lo cual claramente no es posible pues $a$ es un número irracional. Por lo que, la igualdad en (21.2) no se cumple para ningunos enteros $k$ y $j$, es decir que $z^a$ tendrá un número infinito de valores.
   Supongamos ahora que $a=x+iy$, con $y\ne 0$, entonces: $$e^{i2a\pi k}=e^{i2\pi k(x+iy)}=e^{i2\pi kx}{e}^{-2\pi ky},k\in \mathbb{Z},$$ de donde es claro que la expresión $e^{-2\pi ky}$ determina una infinidad de valores distintos para cada $k\in \mathbb{Z}$, por lo que de nueva cuenta $z^a$ tendrá un número infinito de valores.
   Al igual que en el caso 2, cada valor de $k$ determina una rama distinta de la función $z^a$, sin embargo en este caso se tendrá una infinidad de ramas distintas.

Observación 21.10.
Notemos que nuestra definición de potencia compleja es inconsistente con nuestra definición de la exponencial compleja $e^z$. Si tomamos $z=e$ y $a=z^{\prime }\in \mathbb{C}$, entonces: $$e^{z^{\prime }}=e^{z^{\prime }\log (e)}=e^{z^{\prime }\ln (e)}{e}^{i2\pi z^{\prime }k}=e^{z^{\prime }}{e}^{i2\pi z^{\prime }k},k\in \mathbb{Z},$$ la cual es, en general, una función multivaluada. Por tal motivo, siempre que utilicemos la expresión $e^z$ nos referiremos a la función univaluada exponencial compleja.

Para formalizar lo anterior tenemos la siguiente:

Definición 21.6. (Ramas principales de las funciones $b^z$ y $z^a$.)
Sean $a\in \mathbb{C}$ y $b\in \mathbb{C}\setminus \{0\}$. Definimos a la función univaluada exponencial compleja de base $b$ como: $${\exp }_b(z)=b^z=e^{z\mathrm{Log}(b)},z\in \mathbb{C},$$ la cual corresponde con la rama principal de la función multivaluada $b^z$.

Por otra parte, definimos a la función multivaluada potencia compleja, de exponente $a$, como: $$z^a=e^{a\log (z)},z\in \mathbb{C}\setminus \{0\}.$$

Observación 21.11.
Es importante mencionar que en general, no todas las propiedades de las potencias reales con las que estamos familiarizados, se cumplen para el caso complejo.

Sean $a,b\in \mathbb{C}$, $z_1,z_2\in \mathbb{C}\setminus \{0\}$ y $n\in \mathbb{Z}$, en general, no siempre se cumple que:

1. ${\left(z_1{z}_2\right)}^a=z_1^a{z}_2^a$.
2. ${\left(z_1\right)}^{a+b}=z_1^a{z}_1^b$.
3. $z_1^{a-b}={\displaystyle \frac{z_1^a}{z_1^b}}$.
4. ${\left(z_1^a\right)}^n=z_1^{na}$.
5. ${\left(z_1^a\right)}^b=z_1^{ba}$.

Ejemplo 21.12.
a) Sean $z_1=z_2=–1$ y $a=1/2$. Considerando a la rama principal de la función multivaluada $z^a$, tenemos que: $$(z_1{z}_2{)}^a=1^{1/2}=e^{\frac{1}{2}(\mathrm{Log}(1))}=e^0=1,$$

pero: $$z_1^a=z_2^a=(-1{)}^{1/2}=e^{\frac{1}{2}(\mathrm{Log}(-1))}=e^{i\frac{\pi }{2}}=i,$$ de donde $(z_1{z}_2{)}^a=1\ne -1=z_1^a{z}_2^a$.

b) Sean $z_1=–1$ y $a=1/2=-b$. Es claro que $z_1^{a+b}=(-1{)}^0=1$, pero: $$\begin{array}{rl}{z}_1^a=(-1{)}^{1/2}& =e^{\frac{1}{2}(\log (-1))}\\ & =e^{\frac{1}{2}(\mathrm{Log}(-1)+i2\pi m)}\\ & =e^{\frac{1}{2}(i\pi +i2\pi m)}\\ & =e^{i\frac{\pi }{2}}{e}^{i\pi m}\\ & =(-1{)}^{m}i,m\in \mathbb{Z},\end{array}$$ $$\begin{array}{rl}{z}_1^b=(-1{)}^{-1/2}& =e^{-\frac{1}{2}(\log (-1))}\\ & =e^{-\frac{1}{2}(i\pi +i2\pi n)}\\ & =e^{-i\frac{\pi }{2}}{e}^{-i\pi n}\\ & =(-1{)}^n(-i)\\ & =(-1{)}^{n+1}i,n\in \mathbb{Z},\end{array}$$

por lo que: $$z_1^a{z}_1^b=(-1{)}^{m+n+1}{i}^2=(-1{)}^{m+n+1}(-1)=(-1{)}^{m+n+2}=(-1{)}^k,k=m+n+2\in \mathbb{Z},$$ de donde, $z_1^{a+b}=1\ne (-1{)}^k=z_1^a{z}_1^b$ para todo $k\in \mathbb{Z}$ impar.

c) Sean $z_1=a=b=i$. Tenemos que: $$z_1^{ab}=i^{i^2}=i^{-1}=\frac{1}{i}=-i.$$

Por otra parte: $$i^i=e^{i\log (i)}=e^{i^2(\frac{\pi }{2}+2\pi k)}=e^{-(\frac{\pi }{2}+2\pi k)},k\in \mathbb{Z}.$$

Entonces, para toda $k\in \mathbb{Z}$ tenemos que: $$\begin{array}{rl}{\left(z_1^a\right)}^b={\left(i^i\right)}^i={\left(e^{-(\frac{\pi }{2}+2\pi k)}\right)}^i& =e^{i\log \left(e^{-(\frac{\pi }{2}+2\pi k)}\right)}\\ & =e^{i\ln \left(e^{-(\frac{\pi }{2}+2\pi k)}\right)}{e}^{i^2\arg \left(e^{-(\frac{\pi }{2}+2\pi k)}\right)}\\ & =e^{-i\frac{\pi }{2}}{e}^{-i2\pi k}{e}^{-2\pi n}\\ & =-i{e}^{-2\pi n},n\in \mathbb{Z}.\end{array}$$

De donde se sigue que ${\left(z_1^a\right)}^b\ne z_1^{ab}$ para todo $n\in \mathbb{Z}$, con $n\ne 0$.

En este caso, notemos que para $a=b=i$ y $z_1\ne 0$, $z_1^{ab}$ define una función univaluada, mientras que ${\left(z_1^a\right)}^b$ determina una función multivaluada.

Proposición 21.9. (Analicidad de las ramas principales de $z^a$ y $b^z$.)
Sean $a\in \mathbb{C}$ y $b\in \mathbb{C}\setminus \{0\}$. La rama principal de la función multivaluada $z^a$, es decir: $$f(z)=z^a=e^{a\mathrm{Log}(z)},$$ es analítica en $D=\mathbb{C}\setminus (-\mathrm{\infty },0]$ y su derivada es: $$\frac{d}{dz}{z}^a=a{z}^{a-1},\mathrm{\forall }z\in D.$$

Mientras que la rama principal de la función multivaluada $b^z$, es decir: $${\exp }_b(z)=b^z=e^{z\mathrm{Log}(b)},$$ es entera y su derivada es: $$\frac{d}{dz}{b}^z=b^z\mathrm{Log}(b),\mathrm{\forall }z\in \mathbb{C}.$$

Demostración. Dadas las hipótesis, primeramente notemos que la rama principal de la función multivaluada $z^a$ está dada como la composición de las funciones $g(z)=e^z$ y $h(z)=a\mathrm{Log}(z)$, de las cuales $g$ es una función entera y $h$ es analítica en el dominio $D=\mathbb{C}\setminus (-\mathrm{\infty },0]$, por lo que $f=g\circ h$ también será analítica en $D$ y podemos obtener su derivada mediante la regla de la cadena, es decir para todo $z\in D$ tenemos que: $$\frac{d}{dz}{z}^a=\frac{d}{dz}g(h(z))=g^{\prime }(h(z))h^{\prime }(z)=e^{a\mathrm{Log}(z)}\left(\frac{a}{z}\right)=z^a\left(\frac{a}{z}\right)=a{z}^{a-1}.$$

Análogamente, notemos que la rama principal de la función multivaluada $b^z$ está dada como la composición de las funciones $g(z)=e^z$ y $h(z)=z\mathrm{Log}(b)$, las cuales son funciones enteras, por lo que ${\exp }_b=g\circ h$ también es una función entera. Entonces, utilizando la regla de la cadena, para todo $z\in \mathbb{C}$ tenemos que: $$\frac{d}{dz}{b}^z=\frac{d}{dz}g(h(z))=g^{\prime }(h(z))h^{\prime }(z)=e^{z\mathrm{Log}(b)}(\mathrm{Log}(b))=b^z\mathrm{Log}(b).$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 21.13.
Determinemos la rama $f$ de la función multivaluada $F(z)=\sqrt[4]{z-i}$ para la cual $f(1+i)=1$ y calculemos $f(0)$, $f(1)$, $f(-1)$. Veamos donde es analítica $f$ y obtengamos su derivada.

Solución. Notemos que: $$F(z)=\sqrt[4]{z-i}=e^{\frac{1}{4}\log (z-i)}=e^{\frac{1}{4}\mathrm{Log}(z-i)}{e}^{i2\pi \frac{k}{4}},$$ para $k=0,1,2,3$.

Entonces, para cada valor de $k$ obtendremos una rama diferente de $F$.

Dado que $\mathrm{Log}(1)=0$, entonces: $$f(1+i)=F_k(1+i)=e^{\frac{1}{4}\mathrm{Log}(1)}{e}^{i2\pi \frac{k}{4}}=1⟺k=0,$$ por lo que la rama buscada es la función: $$f(z):=F_0(z)=e^{\frac{1}{4}\mathrm{Log}(z-i)}.$$

Tenemos que: $$f(0)=e^{\frac{1}{4}\mathrm{Log}(-i)}=e^{\frac{1}{4}[0-i\frac{\pi }{2}]}=e^{-i\frac{\pi }{8}}.$$ $$f(1)=e^{\frac{1}{4}\mathrm{Log}(1-i)}=e^{\frac{1}{4}[\ln \left(\sqrt{2}\right)-i\frac{\pi }{4}]}=e^{\frac{\ln (2)}{8}}{e}^{-i\frac{\pi }{16}}.$$ $$f(-1)=e^{\frac{1}{4}\mathrm{Log}(-1-i)}=e^{\frac{1}{4}[\ln \left(\sqrt{2}\right)-i\frac{3\pi }{4}]}=e^{\frac{\ln (2)}{8}}{e}^{-i\frac{3\pi }{16}}.$$

Por último, de acuerdo con el ejemplo 21.7(a) sabemos que la función $h(z)=\frac{1}{4}\mathrm{Log}(z-i)$ es analítica en el dominio, figura 81(a): $$D=\mathbb{C}\setminus \{z=x+iy\in \mathbb{C}:x\le 0,y=1\}.$$

Por lo que, al ser $f=g\circ h$, es decir la composición de $g(z)=e^z$ y $h(z)=\frac{1}{4}\mathrm{Log}(z-i)$, entonces $f$ es analítica en $D$ y por la regla de la cadena su derivada es: $$\begin{array}{rl}\frac{d}{dz}f(z)=g^{\prime }(h(z))h^{\prime }(z)& =\left(e^{\frac{1}{4}\mathrm{Log}(z-i)}\right)\frac{1}{4}\left(\frac{1}{z-i}\right)\\ & =\frac{1}{4(z-i)}\left(e^{\frac{1}{4}\mathrm{Log}(z-i)}\right)\\ & =\frac{1}{4(z-i)}\left({(z-i)}^{1/4}\right)\\ & =\frac{1}{4}{(z-i)}^{-\frac{3}{4}}\mathrm{\forall }z\in D.\end{array}$$

En el resultado anterior hemos considerando la rama principal del logaritmo para poder escribir a $f$ como $f(z)={(z-i)}^{1/4}$, es decir estamos trabajando con la rama principal de la función multivaluada $F(z)=\sqrt[4]{z-i}$.

Considerando este hecho, podemos utilizar la regla de la cadena y el resultado dado en la proposición 21.8 para obtener la derivada de $f$ de manera directa, es decir: $$\frac{d}{dz}f(z)=\frac{1}{4}{(z-i)}^{\frac{1}{4}–1}=\frac{1}{4}{(z-i)}^{-\frac{3}{4}},\mathrm{\forall }z\in D.$$

Tarea moral

1. Completa las pruebas de las proposiciones de esta entrada.
2. Determina todas las soluciones para las siguientes ecuaciones.
   a) $e^z=4i$.
   b) $e^{z-1}=-i{e}^3$.
   c) $e^{2z}+e^z+1=0$.
   d) $e^z=2-2i$
3. Determina todos los valores de las siguientes potencias complejas.
   a) ${(-1)}^{3i}$.
   b) ${(-1+i\sqrt{3})}^{3/2}$.
   c) ${(1+i)}^{1-i}$.
   d) ${(-1)}^{\pi }$.
4. Para cada una de las siguientes funciones determina su dominio de analicidad y encuentra su derivada.
   a) $f(z)={\displaystyle \frac{\mathrm{Log}(3z-1)}{z^2+1}}$.
   b) $f(z)=\mathrm{Log}(z^3+1)$.
   c) $f(z)={\mathrm{Log}}_I(z+1)$, con $I=(\frac{\pi }{2},\frac{5\pi }{2})$.
   d) $f(z)=3z^2–e^{i2z}+i\mathrm{Log}(z)$.
5. Considera la función multivaluada $F(z)=z+\sqrt[3]{{(z-1)}^2}$. A partir del corte de rama, figura 82, dado por: $$CR=\{z=x+iy\in \mathbb{C}:x=1,-\mathrm{\infty }<y\le 0\},$$ determina la rama $f$ tal que $f(0)=1$ y calcula $f(1+i)$ y $f(-i)$. ¿Dónde es analítica $f$? Obtén su derivada.
   Hint: Observa que si $z\in \mathbb{C}\setminus CR$, entonces $z–1=|z-1|e^{i\theta }$, con $|z-1|>0$ y $-\frac{\pi }{2}<\theta <\frac{3\pi }{2}$. En particular, para $z_0=0$ se cumple que ${\theta }_0=\pi$.

6. Sean $D\subset \mathbb{C}\setminus \{0\}$ un dominio y $n\in \mathbb{Z}$. Supón que $f:D\to \mathbb{C}$ es una rama del logaritmo en $D$. Prueba que: $$z^n=e^{nf(z)},\mathrm{\forall }z\in D.$$
7. Considera a la función multivaluada $F(z)=\log (iz-1)$. Determina sus puntos de ramificación. Después, considera a la rama principal $f(z)=\mathrm{Log}(iz-1)$. ¿Cuál es el corte de rama de $f$? ¿Cuál es el dominio de analicidad de $f$? Obtén su derivada.
8. Muestra que las tres ramas de la función $z^{1/3}$ son: $$b_1(z)=e^{\frac{1}{3}\mathrm{Log}(z)},b_2(z)=e^{i\frac{2\pi }{3}}{e}^{\frac{1}{3}\mathrm{Log}(z)},b_3(z)=e^{i\frac{4\pi }{3}}{e}^{\frac{1}{3}\mathrm{Log}(z)}.$$ ¿Cuál es el dominio de analicidad de cada rama? Determina la derivada de cada rama.
9. Considera la función multivaluada $F(z)=\sqrt[4]{z}$. Utilizando la rama natural del logaritmo, determina la rama $f$ tal que $f(-1)=\frac{\sqrt{2}}{2}(1+i)$. ¿Cuál es el dominio de analicidad de $f$?. Determina el valor de $f^{\prime }(-i)$.
   Hint: Recuerda que la rama natural del logaritmo es: $${\mathrm{Log}}_{(0,2\pi )}(z)=\ln |z|+i{\mathrm{Arg}}_{(0,2\pi )}(z),$$ la cual es analítica en el dominio $D=\mathbb{C}\setminus [0,\mathrm{\infty })$.
10. Muestra que las funciones $f_1(z)=\mathrm{Log}(1-z)$ y $f_2(z)=\mathrm{Log}(1+z)$ son analíticas, respectivamente, en los dominios: $$D_1=\mathbb{C}\setminus A_1\text{y}{D}_2=\mathbb{C}\setminus A_2,$$ donde: $$\begin{array}{r}{A}_1=\{z\in \mathbb{C}:\mathrm{Re}(z)\ge 1,\mathrm{Im}(z)=0\},\\ A_2=\{z\in \mathbb{C}:\mathrm{Re}(z)\le -1,\mathrm{Im}(z)=0\}.\end{array}$$

Más adelante…

En esta entrada hemos dado una definición para las funciones logaritmo y exponecial complejas. A diferencia de sus versiones reales, vimos que estas funciones son, en general, multivaluadas, por lo que debemos elegir alguna rama para poder estudiar las propiedades de cada una de estas funciones, como la continuidad y analicidad. Por simplicidad es común trabajar con las ramas principales, sin embargo en ciertas ocasiones cambiar de ramas nos permitirá resolver algún problema de manera más sencilla.

De acuerdo con los resultados de esta entrada, vimos que la rama principal del logaritmo extiende al logaritmo natural real y que nos permite obtener logaritmos para número reales negativos. Además de que bajo ciertas restricciones esta rama es una de las inversas de la función exponencial compleja.

Para el caso de las potencias complejas, vimos que, en general, no se cumplen las propiedades de las potencias reales con las que estamos familiarizados. Sin embargo, trabajar con potencias complejas nos facilita el trabajo a la hora de determinar ramas específicas de una función multivaluada.

La siguiente entrada definiremos otras funciones elementales, las funciones trigonométricas e hiperbólicas y estudiaremos algunas de sus propiedades más elementales. Veremos que a través de la exponencial y el logaritmo podremos definir a estas funciones y sus inversas.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Exponencial compleja.
• Siguiente entrada del curso: Funciones trigonométricas e hiperbólicas complejas.