$ \textit{ MATERIAL EN REVISIÓN}$
Introducción
Probablemente recuerdes que en los cursos de Cálculo Diferencial e Integral se habló de bolas de radio $\varepsilon>0$ con centro en un punto $x$. Había otros conjuntos, como los conjuntos abiertos y cerrados, de los que habrás visto representaciones gráficas, (puedes consultar la entrada $\mathbb{R}^n$ como espacio Topológico para tener presente los conceptos en la métrica usual). Estas ideas pueden generalizarse a otros espacios con métrica distinta a la euclidiana. En la sección que aquí se presenta visualizaremos algunos ejemplos y comprobarás que conjuntos como la bola abierta, quedan representados por figuras diferentes a las ya conocidas (no siempre se trata de círculos o esferas). Observarás los cambios que las métricas pueden generar, incluso cuando también se trata de distancias en el conjunto $\mathbb {R}^n$.
Comencemos por identificar puntos que estén “cerca” entre sí, aquellos cuya distancia no exceda cierta cantidad. Para eso tenemos la siguiente:
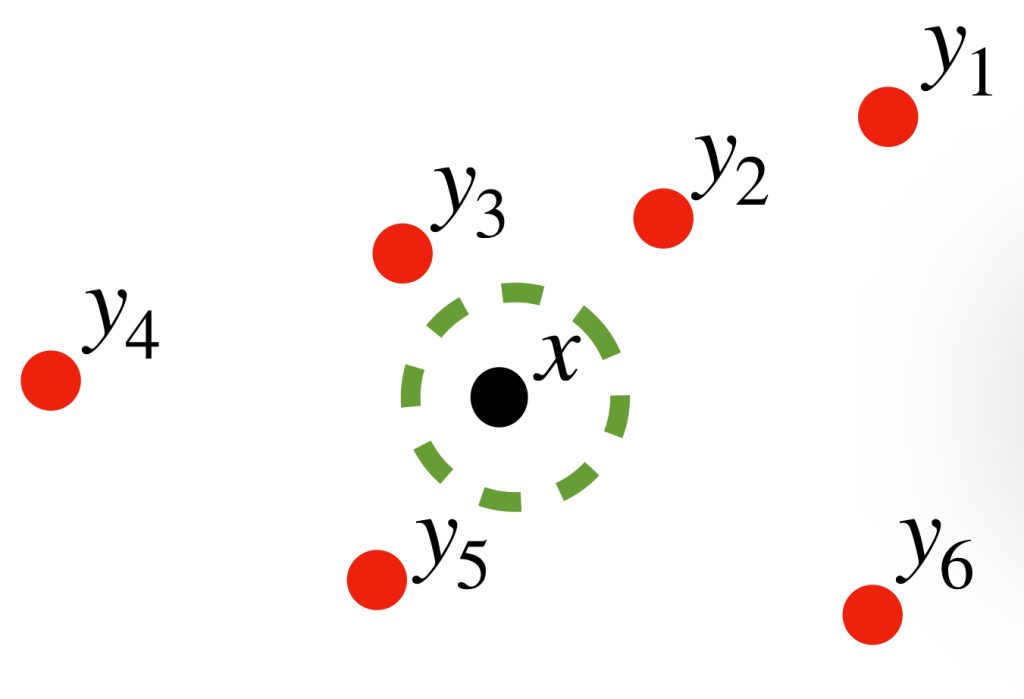
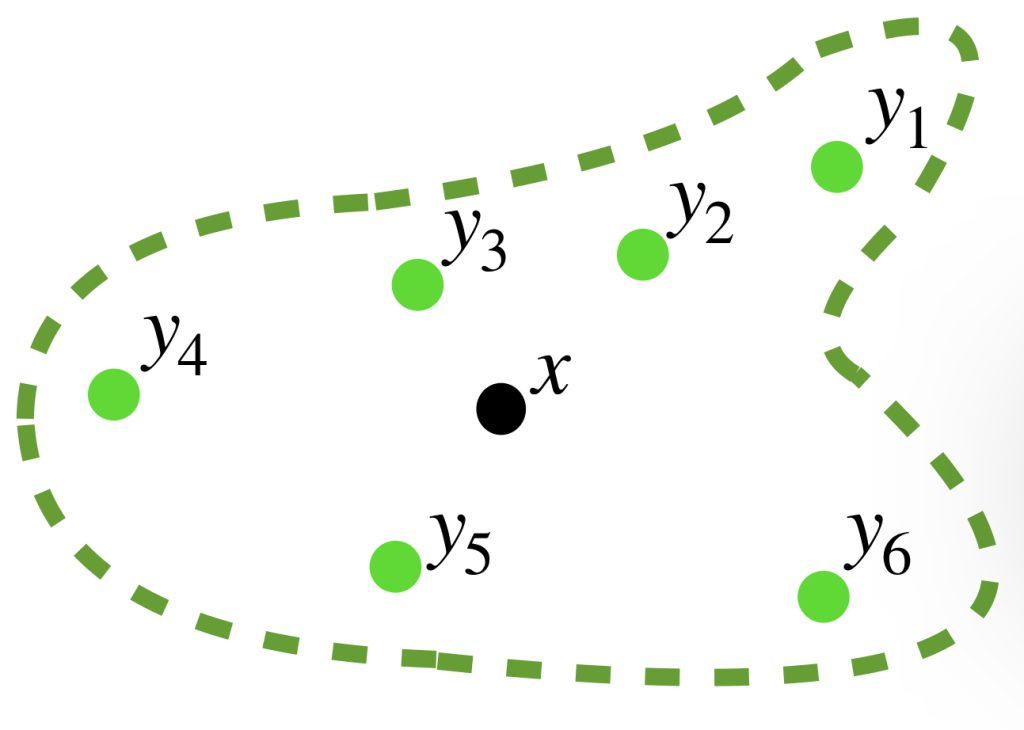
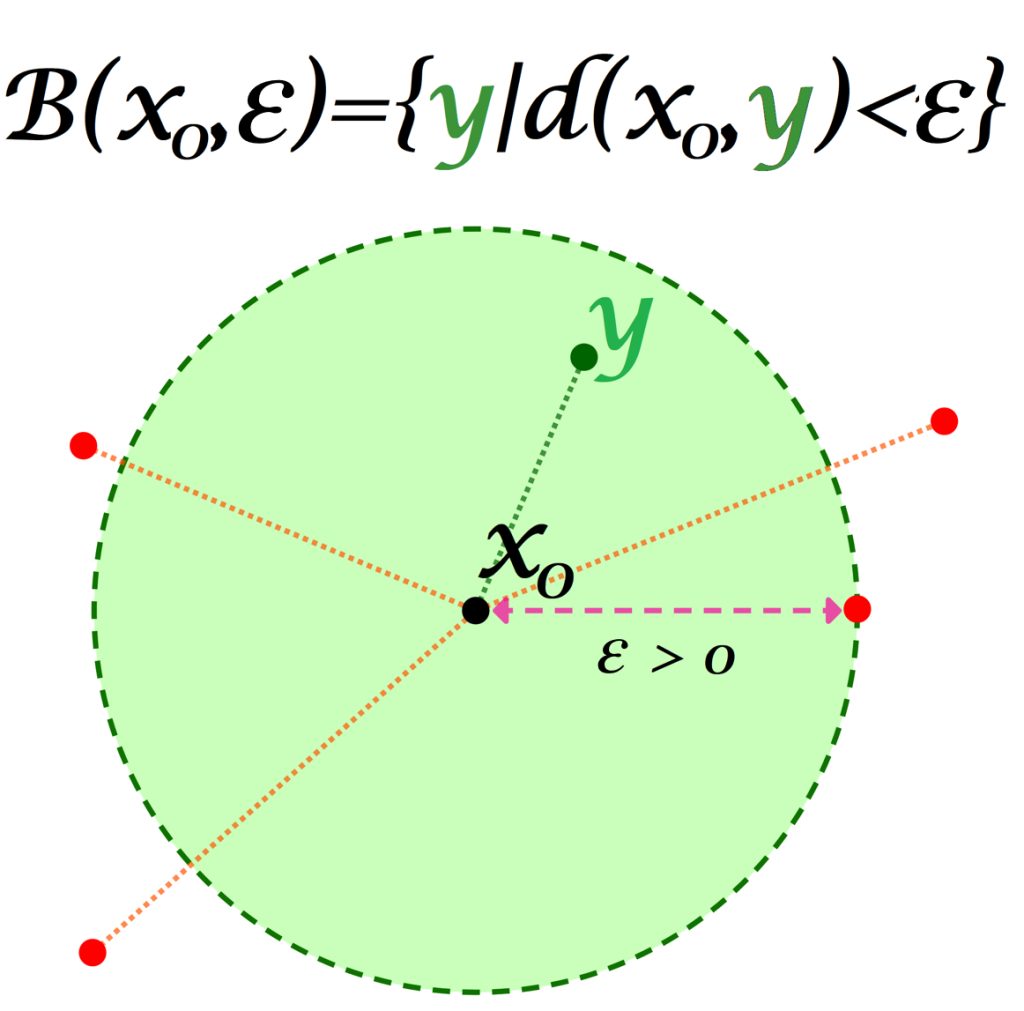
Definición. Bola abierta. Sea $(X,d)$ un espacio métrico. Considera un punto $x \in X$ y $\varepsilon \in \mathbb {R}$ tal que $\varepsilon>0$. La bola abierta con centro en $x$ y radio $\varepsilon$ se define como el conjunto de puntos en $X$ tales que el valor de su distancia al punto $x$ es menor que $\varepsilon$. Se denota como:
$$B(x,\varepsilon) := \{y \in X | d(x,y) < \varepsilon\}$$
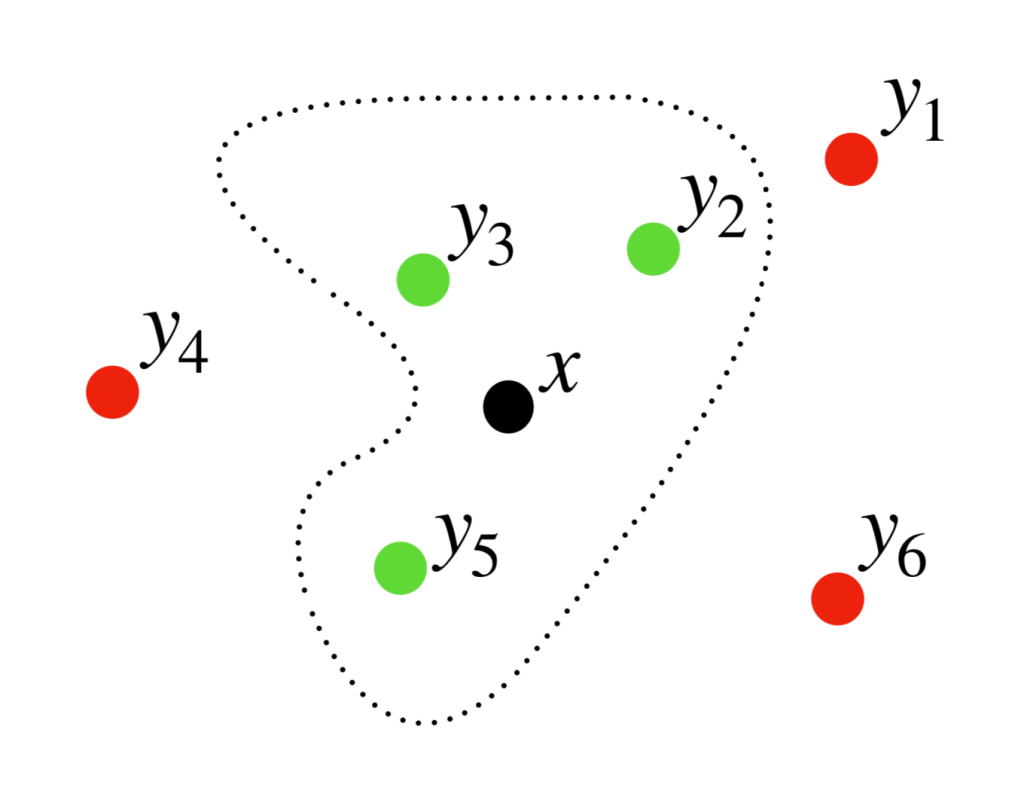
Nota que si $x$ es el centro, entonces siempre está en la bola abierta sin importar el valor de $\varepsilon > 0$, pues precisamente, $d(x,x)=0<\varepsilon$
Ejemplos de bolas abiertas en espacios métricos
La bola abierta en la métrica discreta
Recordemos que en la métrica discreta, la distancia entre dos puntos diferentes siempre es $1$. Entonces, si $0<\varepsilon<1$ la bola abierta solo tendrá como elemento al centro.
Por el contrario, si $\varepsilon>1$ la bola abierta tendrá como elementos a todos los elementos del espacio métrico.
La bola abierta en $\mathbb{R}$ con la métrica euclidiana
Considera el conjunto $\mathbb{R}$ con la métrica usual.
\[
d(x,y) := |x-y| := \left\{ \begin{array}{lcc}
x-y & si & x \geq y \\
\\ y-x & si & x < y
\end{array}
\right.
\]
Para $x,y \in \mathbb{R}$
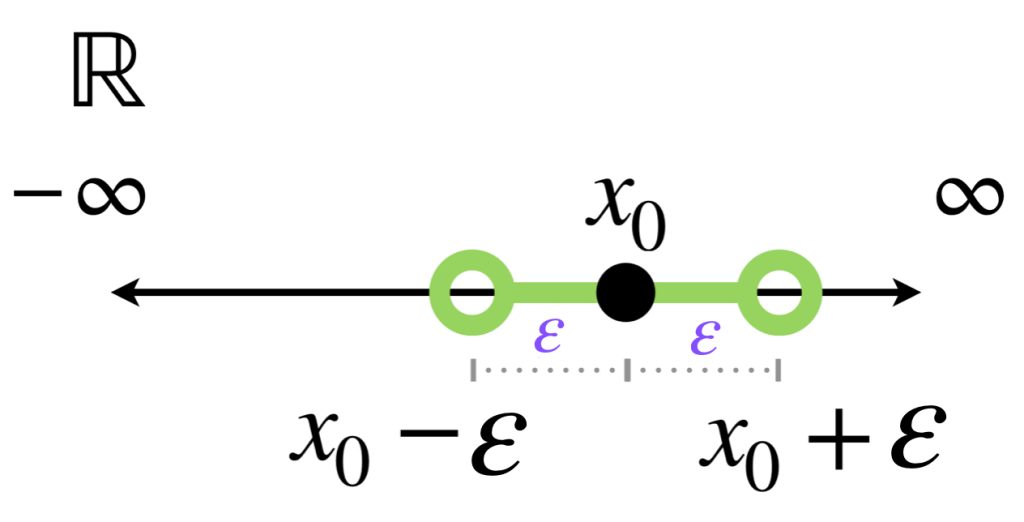
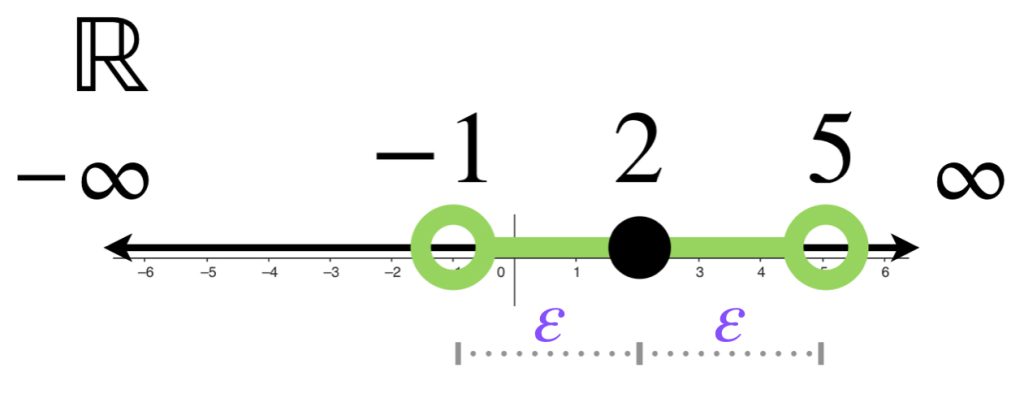
Entonces para un punto $x_{0} \in \mathbb{R}$ y $\varepsilon>0$, la bola abierta $B(x_0,\varepsilon)$ está dada por el intervalo abierto $(x_{0}-\varepsilon,x_{0}+\varepsilon)$.
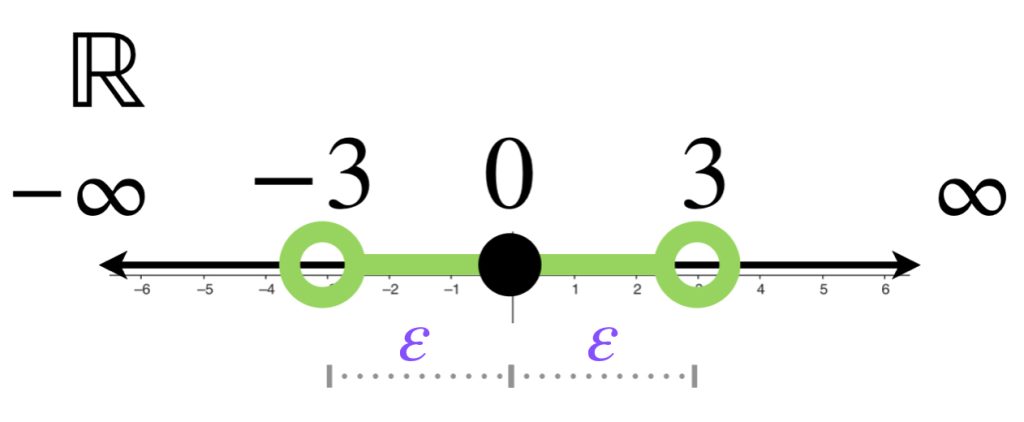
Más específicamente, la bola abierta con centro en $0$ y radio $3$ es el intervalo $(-3,3)$.
Mientras que la bola abierta con centro en $2$ y radio $3$ es el intervalo $(-1,5)$.
La bola abierta en $\mathbb{R}^2$ con la métrica euclidiana
Considera ahora $\mathbb{R}^2$ y la métrica euclidiana definida por:
$$d(x,y) := \sqrt{(x_{1}-y_{1})^2+(x_{2}-y_{2})^2}$$
con $x=(x_{1},x_{2})$ y $y=(y_{1},y_{2}) \in \mathbb{R}^2$.
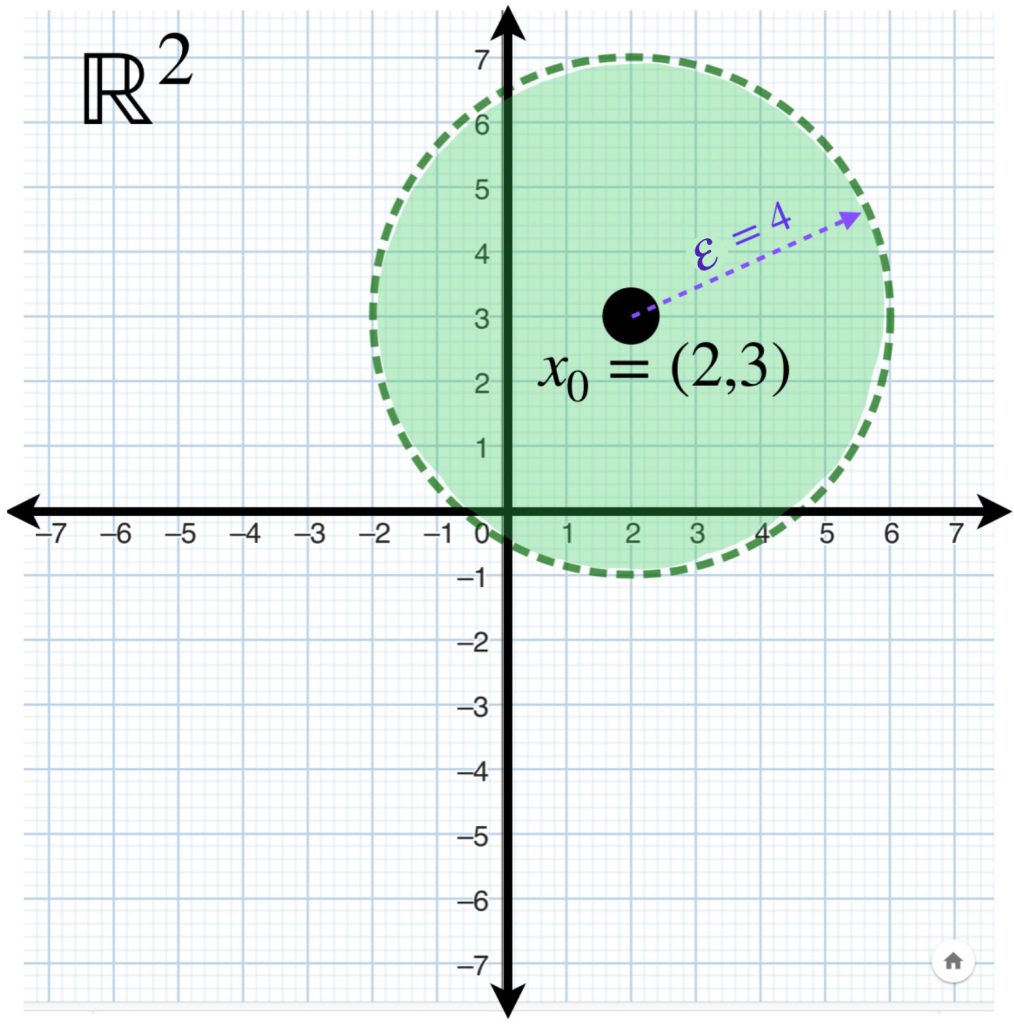
Entonces para un punto $x_{0}=(x_{0_1},x_{0_2}) \in \mathbb{R}^2$ y $\varepsilon>0$, la bola abierta $B(x_0,\varepsilon)$ está dada por el conjunto de puntos que están «dentro de la circunferencia» con centro en $x_0$ y radio $\varepsilon$.
Por ejemplo, si $x_0=(2,3)$ y $\varepsilon=4$ la bola abierta $B((2,3),4)$ está formada por los puntos dentro de la circunferencia con centro en $(2,3)$ y radio $4$.
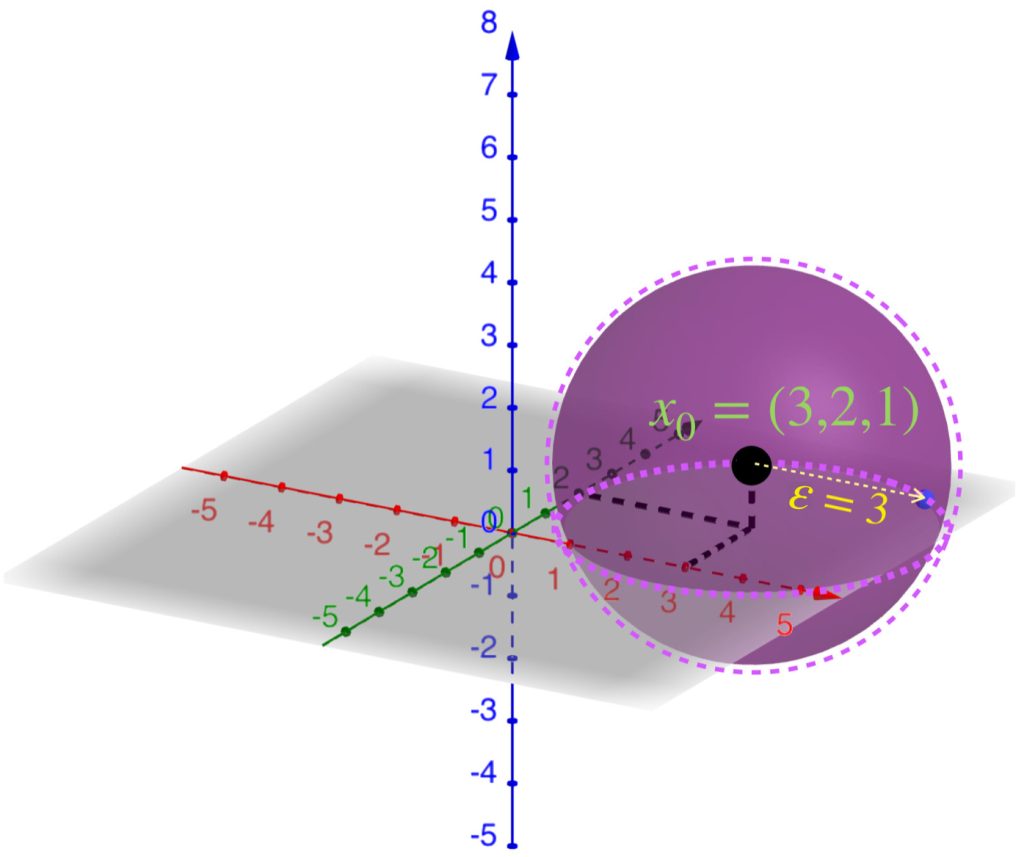
La bola abierta en $\mathbb{R}^3$ con la métrica euclidiana
Si pensamos en $\mathbb{R}^3$ y la métrica euclidiana definida por:
$$d(x,y) := \sqrt{(x_{1}-y_{1})^2+(x_{2}-y_{2})^2+(x_{3}-y_{3})^2}$$
con $x=(x_{1},x_{2},x_{3})$ y $y=(y_{1},y_{2},y_{3}) \in \mathbb{R}^3$.
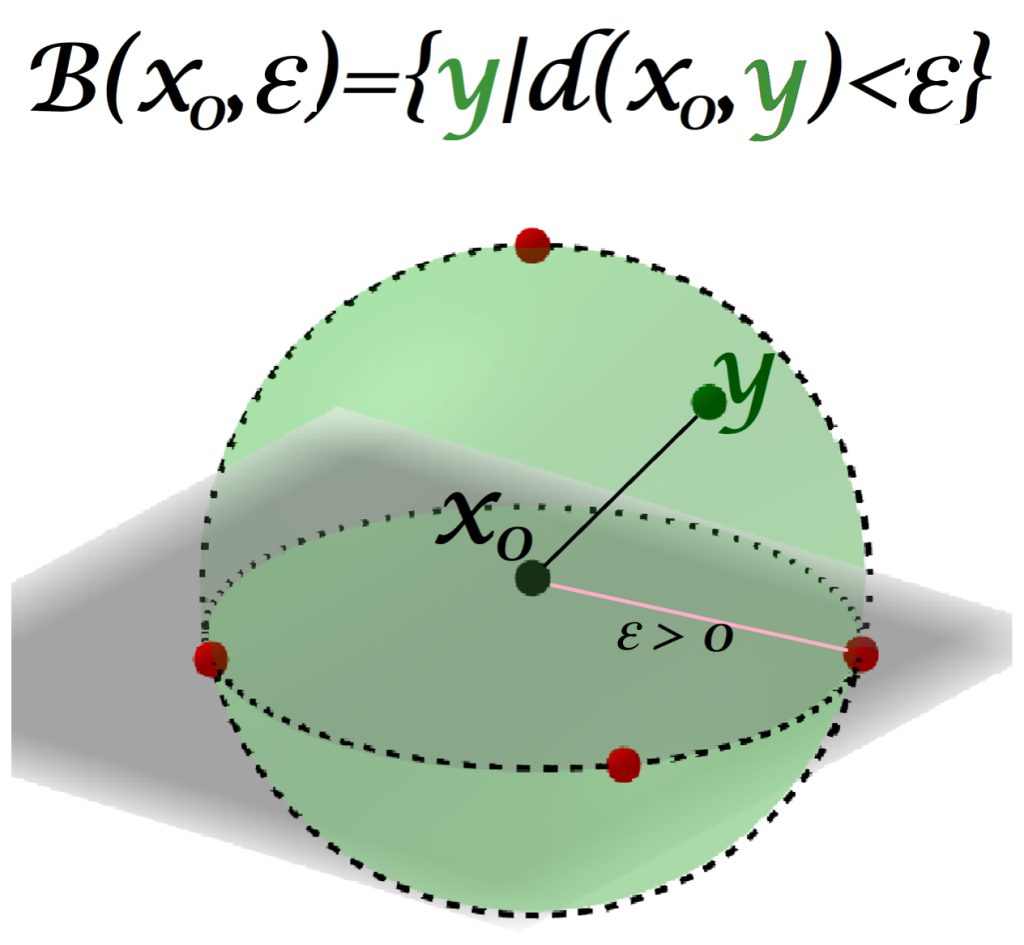
Entonces para un punto $x_0=(x_{0_1},x_{0_2},x_{0_3}) \in \mathbb{R}^3$ y $\varepsilon>0$, la bola abierta $B(x_0,\varepsilon)$ está dada por el conjunto de puntos que están «dentro de la esfera» con centro en $x_0$ y radio $\varepsilon$.
Por ejemplo, si $x_0=(3,2,1)$ y $\varepsilon=3$, la bola abierta $B((3,2,1),3)$ está formada por los puntos “dentro de la esfera” con centro en $(3,2,1)$ y radio $3$.
La bola abierta en la métrica del taxista
En la sección Otros ejemplos de espacios métricos definimos esta métrica en el conjunto $\mathbb{R}^2$ como:
$$d(x,y) :=|y_1-x_1|+|y_2-x_2| $$
para $x=(x_{1},x_{2})$ y $y=(y_{1},y_{2}) \in \mathbb{R}^2$.
Entonces para un punto $x_{0}=(x_{0_1},x_{0_2}) \in \mathbb{R}^2$ y $\varepsilon >0$, la bola abierta $B(x_{0},\varepsilon )$ está dado por el conjunto de puntos $y=(y_{1},y_{2}) \in \mathbb{R}^2$ que satisfacen:
\begin{align*}
d(x_{0},y)=|y_1-x_{0_1}|+|y_2-x_{0_2}|&< \varepsilon \\
\Leftrightarrow |y_2-x_{0_2}|&< \varepsilon -|y_1-x_{0_1}| \\
\Leftrightarrow – \varepsilon +|y_1-x_{0_1}|< y_2-x_{0_2}&< \varepsilon -|y_1-x_{0_1}|
\end{align*}
Esto quiere decir que el conjunto buscado está delimitado por las rectas:
\begin{align}
y_{2}-x_{0_2}&= \varepsilon -(y_1-x_{0_1})\\
y_{2}-x_{0_2}&= \varepsilon +(y_1-x_{0_1})\\
y_{2}-x_{0_2}&= – \varepsilon -(y_1-x_{0_1})\\
y_{2}-x_{0_2}&= – \varepsilon +(y_1-x_{0_1})
\end{align}
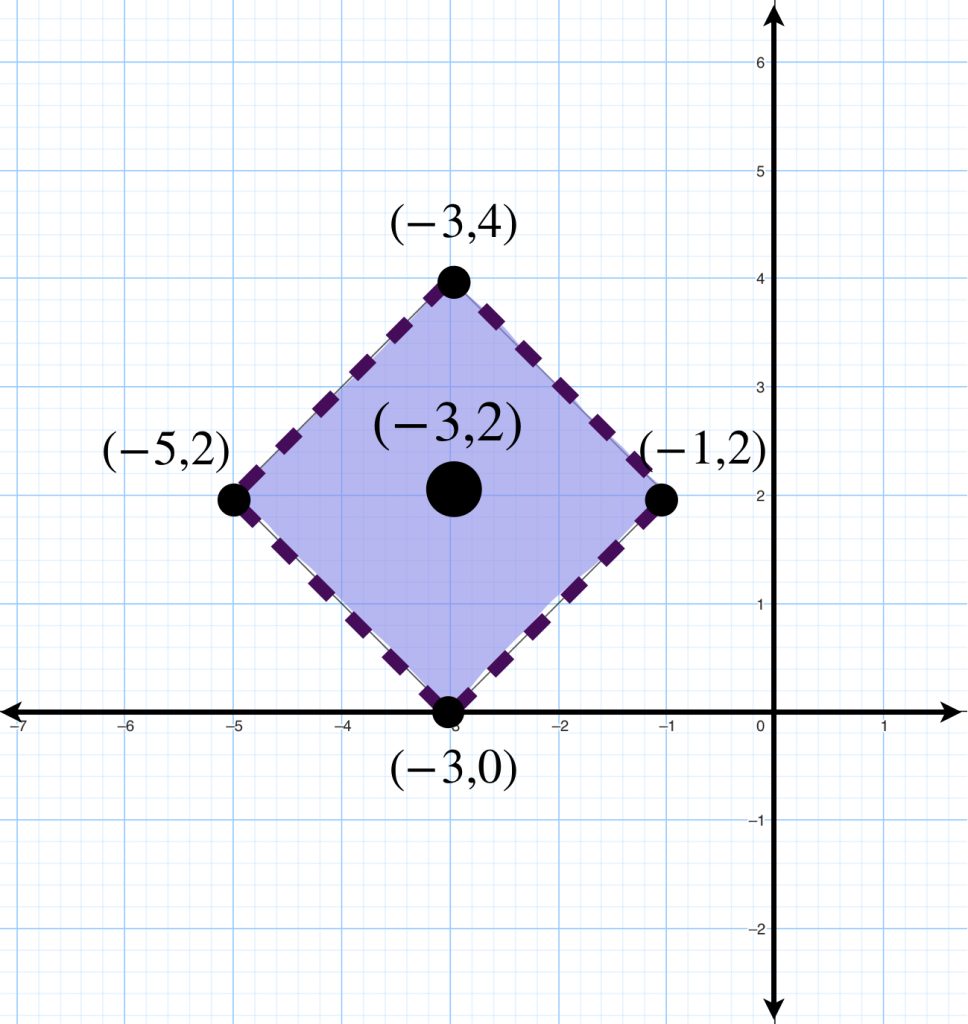
Que son representadas a continuación:
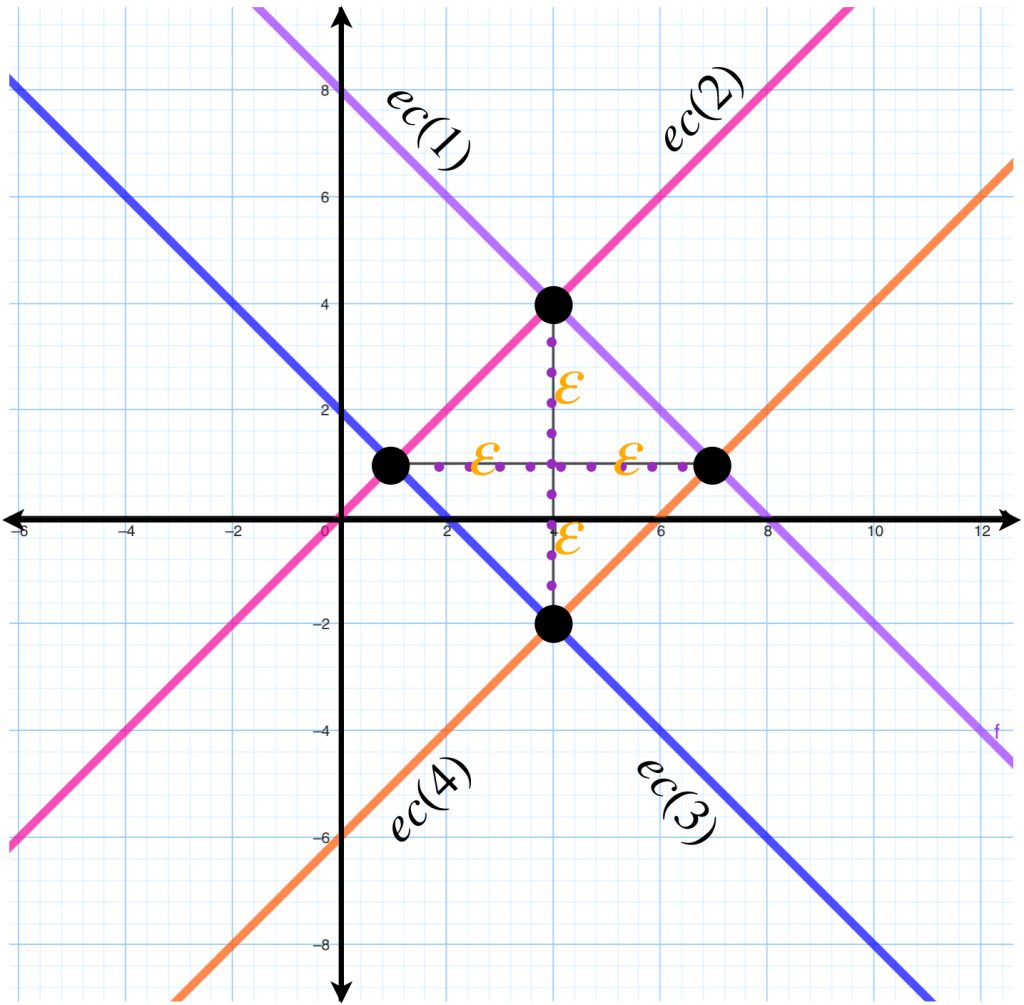
Como la desigualdad es estricta concluimos que la bola abierta será un «rombo abierto» cuyas diagonales tienen longitud $2\varepsilon$ con centro en el punto $x_{0}=(x_{0_1},x_{0_2})$.
Como ejemplo considera la bola abierta con centro en $(-3,2)$ y de radio $2$. El conjunto $B((-3,2),2)$ se muestra en la siguiente imagen.
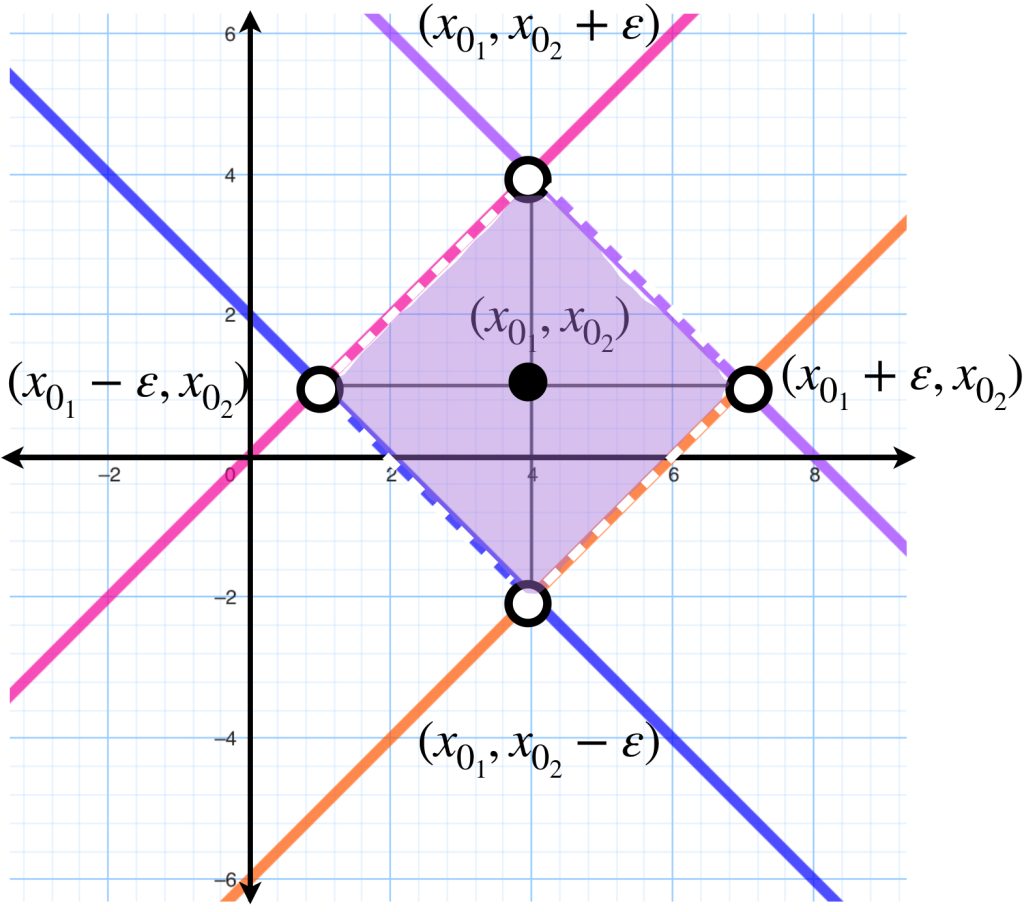
La bola abierta en la métrica del ascensor
Recordemos que el desplazamiento entre dos pisos de edificios iguales o diferentes motiva una métrica en $\mathbb{R}^2$. (Ver Otros ejemplos de espacios métricos). Si estamos en el piso marcado con el punto $x_{0}=(x_{0_1},x_{0_2}) \in \mathbb{R}^2$ y tenemos $\varepsilon>0$ como límite de distancia, procedamos a identificar los puntos a los que podemos llegar:
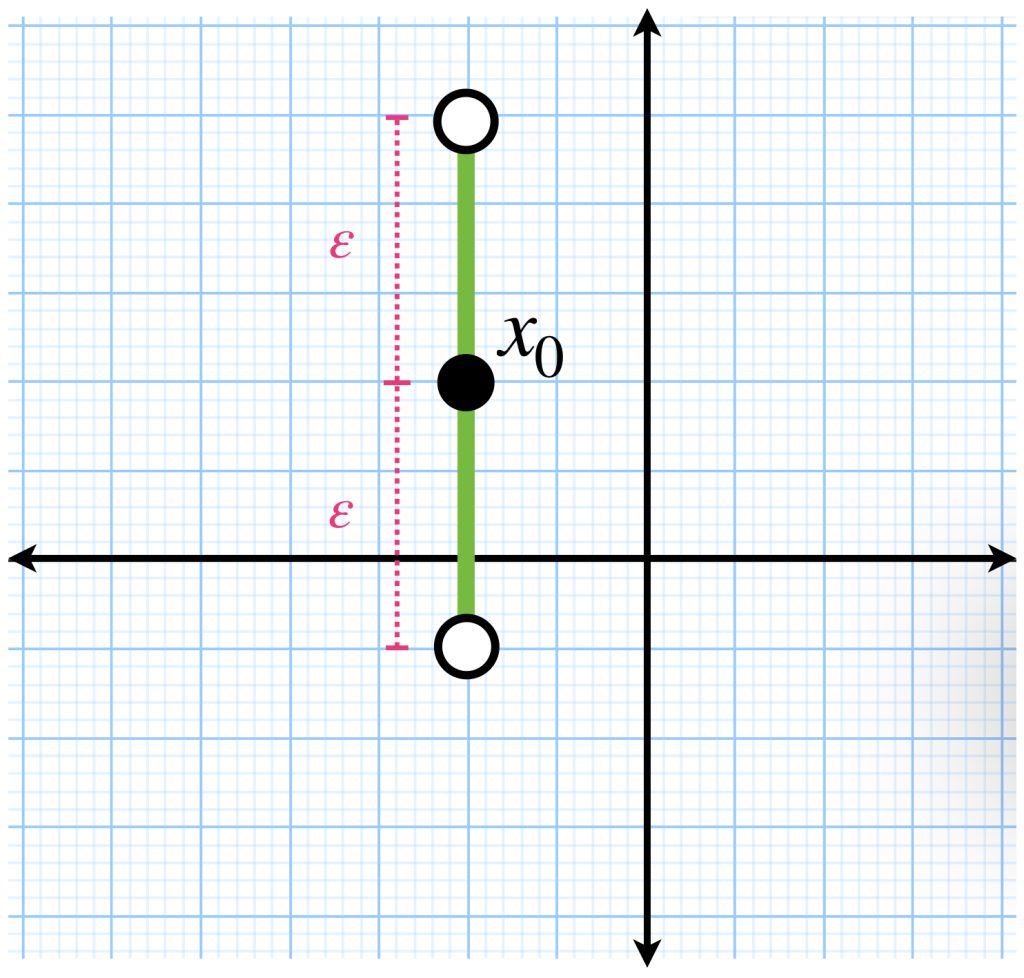
Estando en el mismo edificio, el ascensor puede llevarnos hasta una distancia menor que $\varepsilon$ hacia arriba, o bien, una distancia menor que $\varepsilon$ hacia abajo.
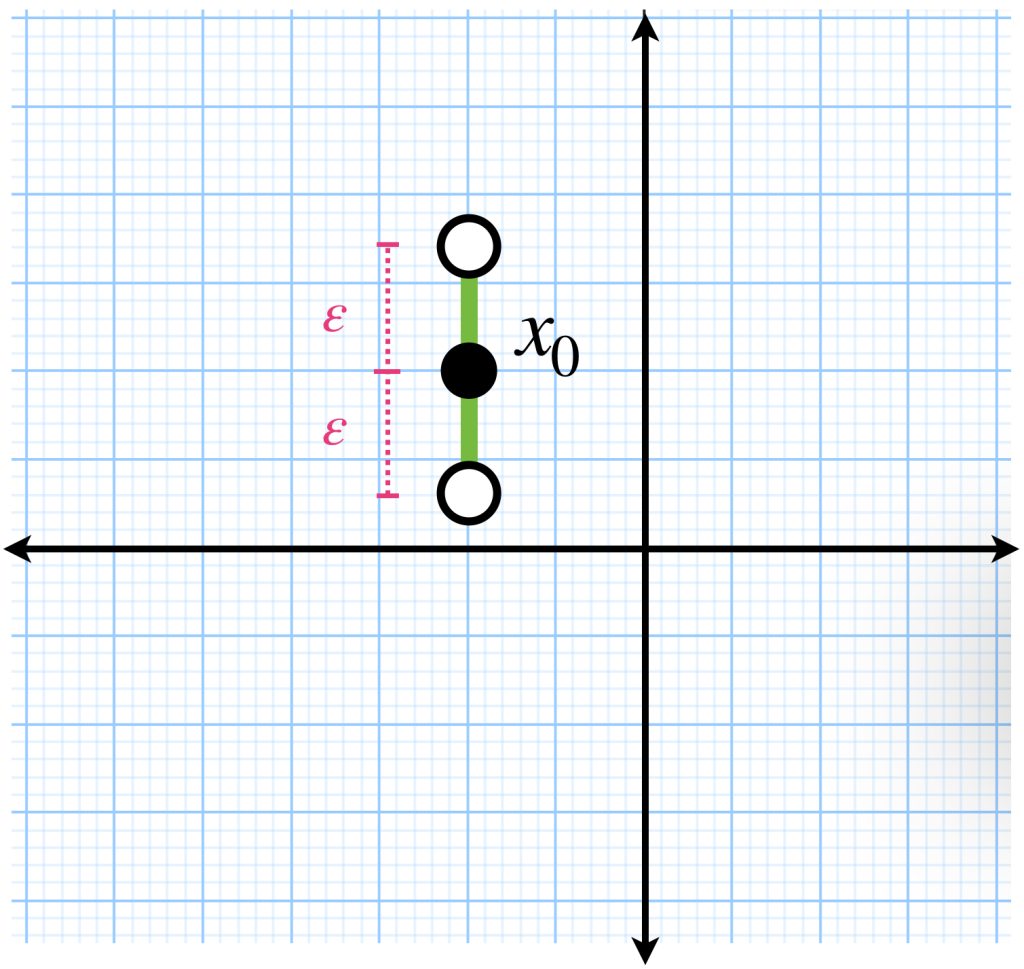
Como la planta baja está a distancia $\varepsilon_1:=|x_{0_2}|$ entonces si $\varepsilon_1> \varepsilon$, nuestro ascensor no llega hasta ahí.
En contraparte, si $\varepsilon_1 \leq \varepsilon$, entonces sí podemos llegar a la planta baja y, quizá también, a otros niveles del «sótano».
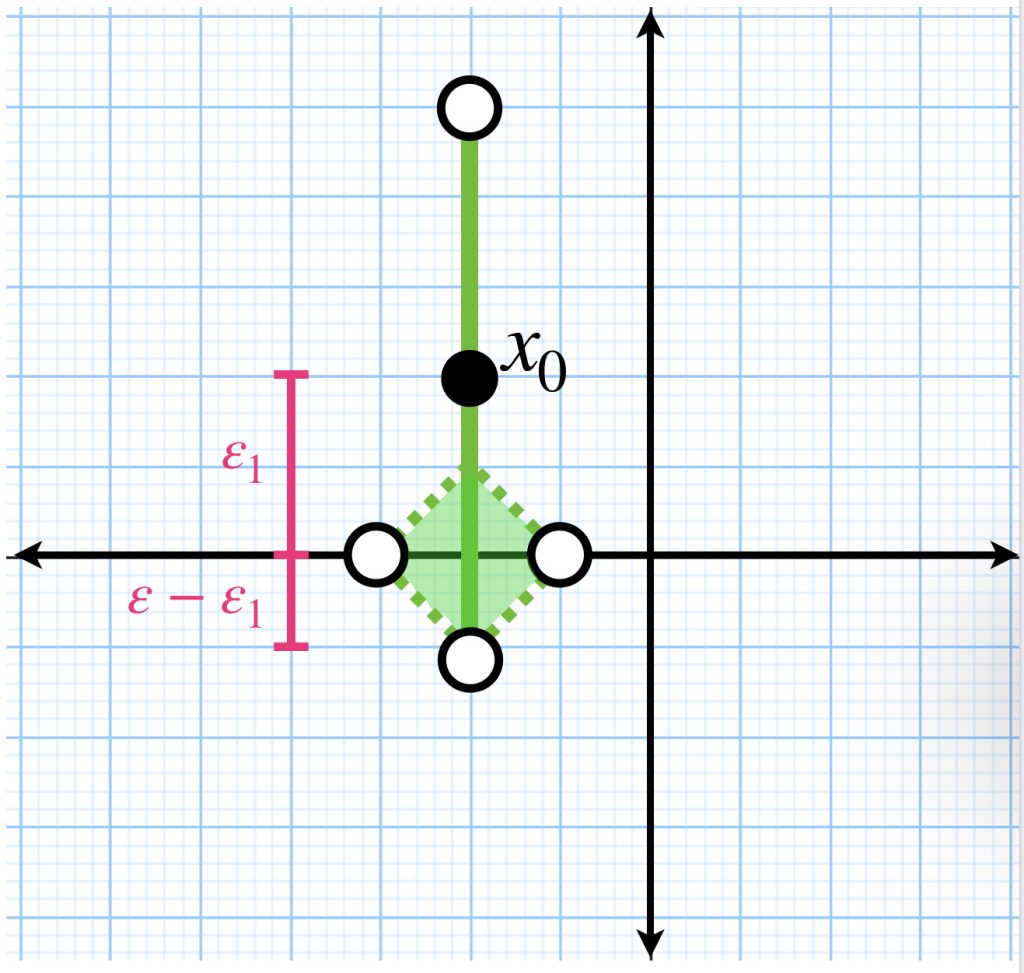
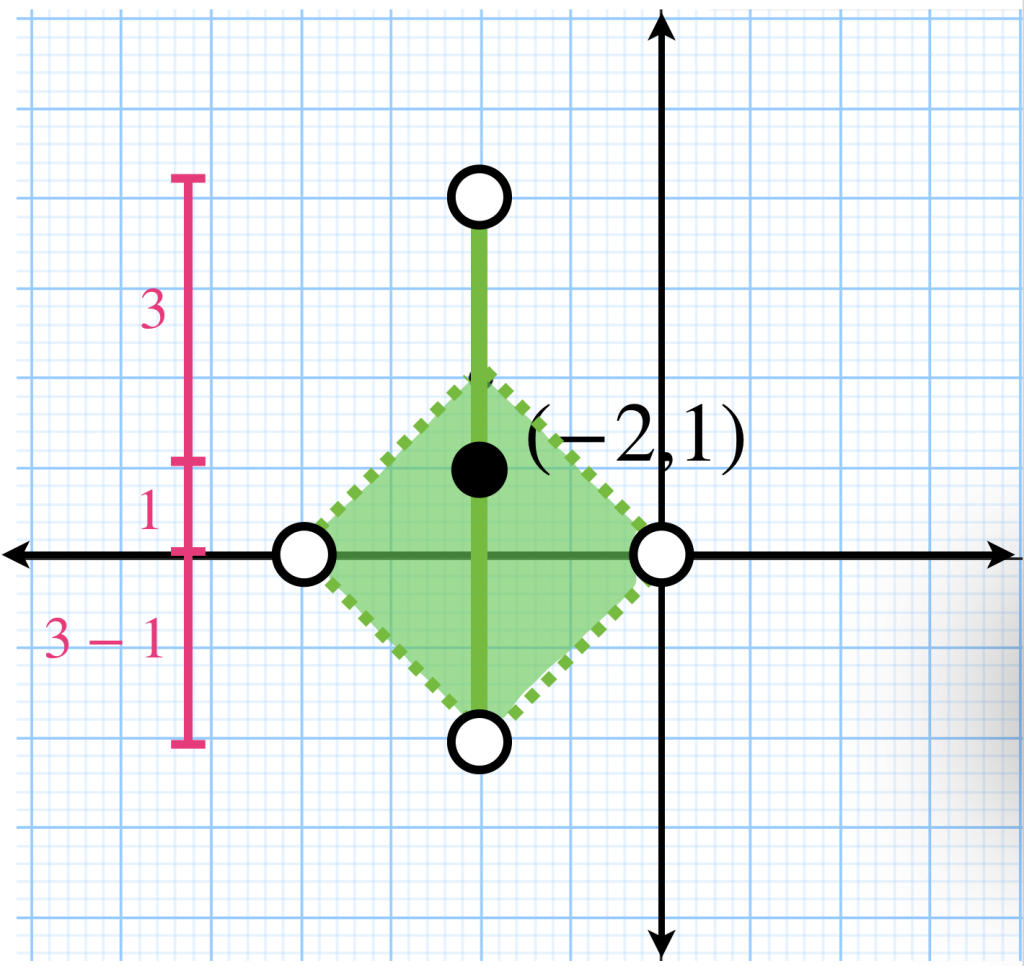
En este caso, aún nos podemos desplazar hasta una distancia $\varepsilon-\varepsilon_1$, primero sobre el eje $x$ y luego sobre el eje $y$ a modo de la métrica del taxista. En consecuencia, la bola abierta está conformado por una linea vertical de longitud $2\varepsilon$, sin los extremos, que tiene centro en el punto $x_{0}=(x_{0_1},x_{0_2})$. Si $\varepsilon_1 < \varepsilon$, se agrega también a la bola abierta, un «rombo abierto» con centro en el punto $(x_{0_1},0)$ cuyas diagonales miden $2(\varepsilon-\varepsilon_1)$. Esto se representa en la siguiente imagen:
Como ejemplo, la bola con centro en $(-2,1)$ y radio $3$ tendrá la siguiente representación:
La bola abierta en el tablero de ajedrez.
Hemos visto que en un conjunto dado por las casillas del tablero de ajedrez se pueden definir métricas de acuerdo al movimiento de cada pieza. Como ejemplo, considera el movimiento permitido para la reina. Sea $x_0$ la casilla donde se encuentra. En cada turno, esta pieza se puede mover en cualquier dirección y cualquier cantidad de casillas. Como la distancia entre dos casillas se define como el mínimo de movimientos necesarios para que la pieza llegue de una casilla a la otra, entonces tenemos las siguientes bolas abiertas para distintos valores de $\varepsilon$:
Si $0<\varepsilon \leq 1$ entonces la distancia entre dos casillas debe ser menor que $1$. En consecuencia buscamos señalar las casillas a las que se puede desplazar la reina en $0$ movimientos que es, únicamente, la casilla en la que está posicionada.
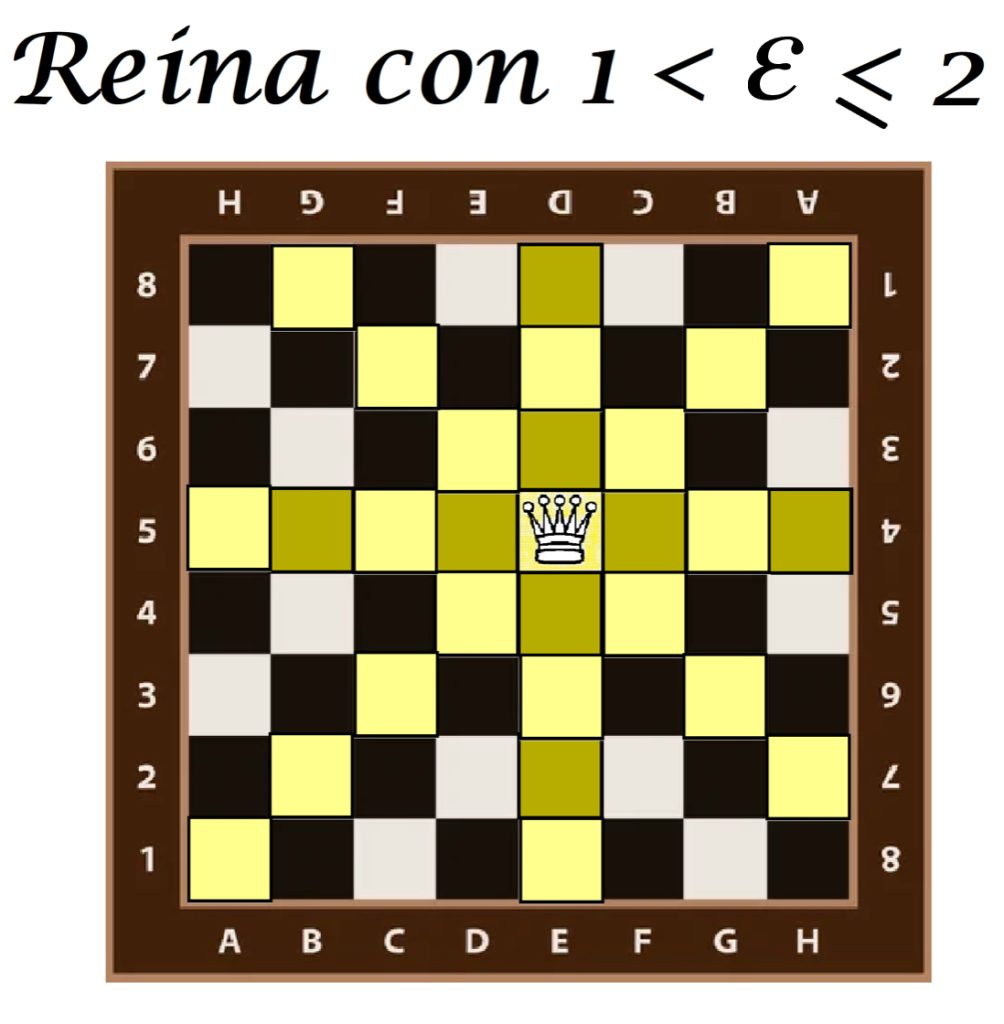
Si $1<\varepsilon \leq 2$ entonces se permite hacer a lo más un movimiento. Las casillas a las que se puede desplazar la reina están señaladas en tonos amarillos, pues puede elegir cualquier dirección y elegir también, detenerse en cualquiera de ellas.
Si $2<\varepsilon$ entonces ya se permiten hacer 2 movimientos. En la figura anterior podemos visualizar casillas no sombreadas en amarillo. No obstante a cualquiera de ellas se puede llegar desde alguna de las casillas iluminadas. En consecuencia, con dos movimientos es posible que la reina llegue a cualquier casilla del tablero.
En contraparte el rey, que también se puede mover en cualquier dirección, no puede avanzar más que una casilla por turno. Esto origina las siguientes representaciones de bolas abiertas:
Para $\varepsilon \leq 1$ el rey no puede hacer ningún movimento y permanece en la casilla donde esté ubicado.
Para $1 <\varepsilon \leq 2$ el rey puede hacer un movimiento y acceder así, a las casillas adyacentes a su posición.
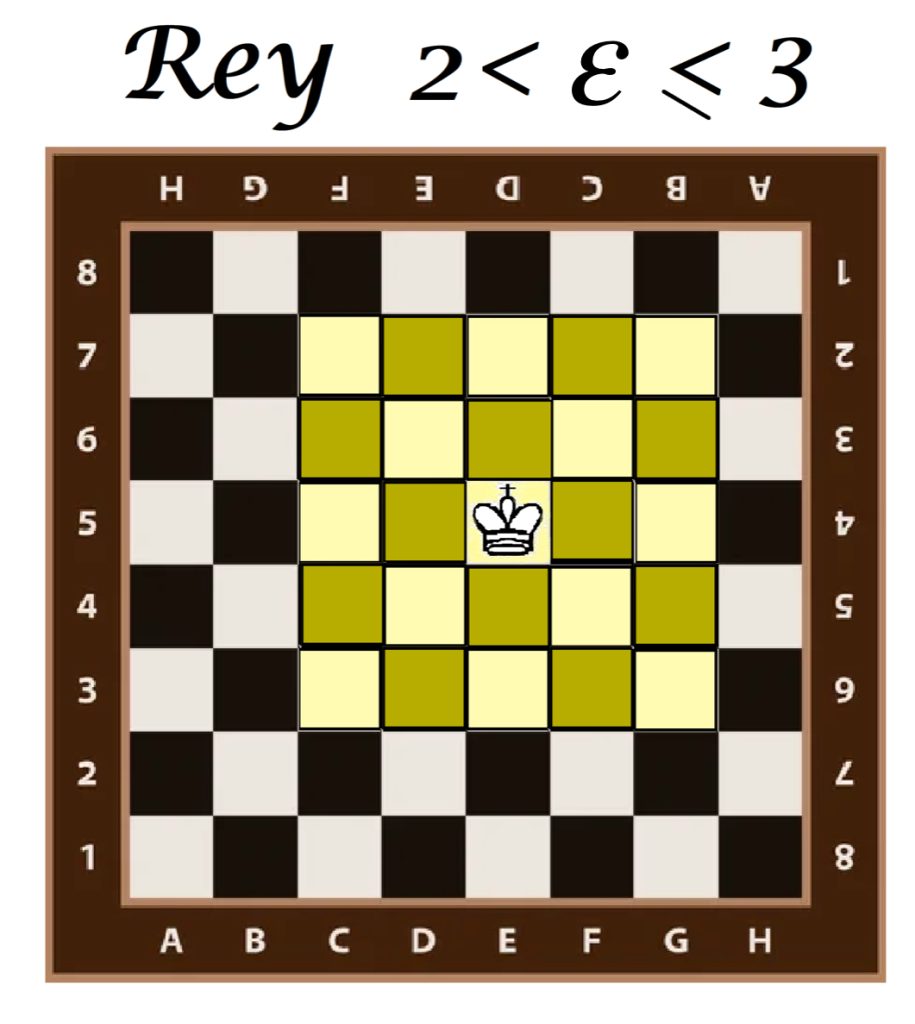
Para $2 <\varepsilon \leq 3$ el rey puede avanzar hasta dos casillas, lo que se representa iluminando las casillas vecinas con respecto a la imagen anterior.
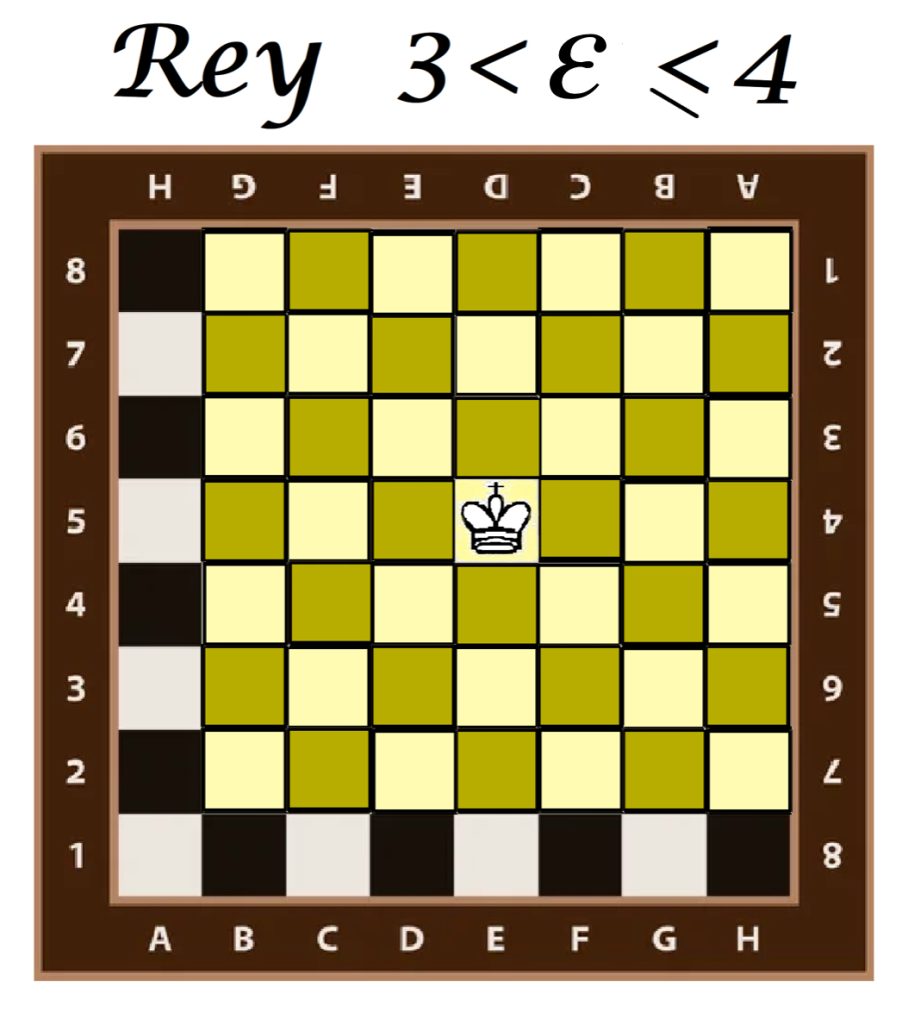
Para $3 <\varepsilon \leq 4$ una nueva familia de casillas vecinas se agrega a la bola abierta. ¿Puedes decir entonces, cuál es la distancia más grande entre dos casillas con la métrica del rey? ¿Y con la de la reina?
Más adelante
Retomaremos los conceptos de interior, cerradura o frontera de un conjunto, así como de conjunto abierto y cerrado vistos en los cursos de Cálculo pero ahora generalizados en cualquier espacio métrico.
Tarea moral
- Representa las bolas abiertas en la métrica del ajedrez con otras piezas.
- Muestra un ejemplo de bola abierta en la métrica del ascensor en el que el centro esté fuera del rombo, uno donde esté dentro y uno más donde el centro esté sobre el vértice.
- Da un ejemplo de espacio métrico y dos bolas $B(x,\varepsilon_1)$ y $B(y,\varepsilon_2)$ tales que $\varepsilon_1>\varepsilon_2$ pero $B(x,\varepsilon_1) \subset B(y,\varepsilon_2)$.
Bibliografía
- Chugani,V., Understanding Chebyshev Distance: A Comprehensive Guide. DataCamp. 2024.
- Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 36 y 37.
- Losada, R. La geometría del Taxi. Boletín de la Sociedad Puig Adam de Profesores de Matemáticas, 116, 2023, págs 10-37.
- Toledo, F., Topología de Espacios Métricos Animada con GeoGebra. Pereira: Universidad Tecnológica de Pereira. 2017, págs 29-31.