Introducción
A lo largo de los temas hemos visto definiciones de inversión junto con teoremas, pero también podemos verlo a través de construcciones a la inversión usando regla y compas.
Construcciones
Construcción. Dada una línea que pasa por $A$ y $B$, encontrar el punto medio del segmento $AB$ usando únicamente compas.
Solución. Podemos construir una circunferencia con centro $A$ y radio $AB=r$ se tiene $C(A,r)$ y con esta localizamos $P$ en la línea $AB$ talque $B$ es el punto medio de $AP$. Usando $P$ como centro y radio $AP$ trazamos la circunferencia $C(P,AP)$ la cual interseca a la primera circunferencia $C(A,r)$ en un punto $C$. Por último dibujamos la circunferencia $C(C,r=AB)$ donde intersecamos a $AB$ en $P’$, entonces $P’$ es punto medio de $AB$.
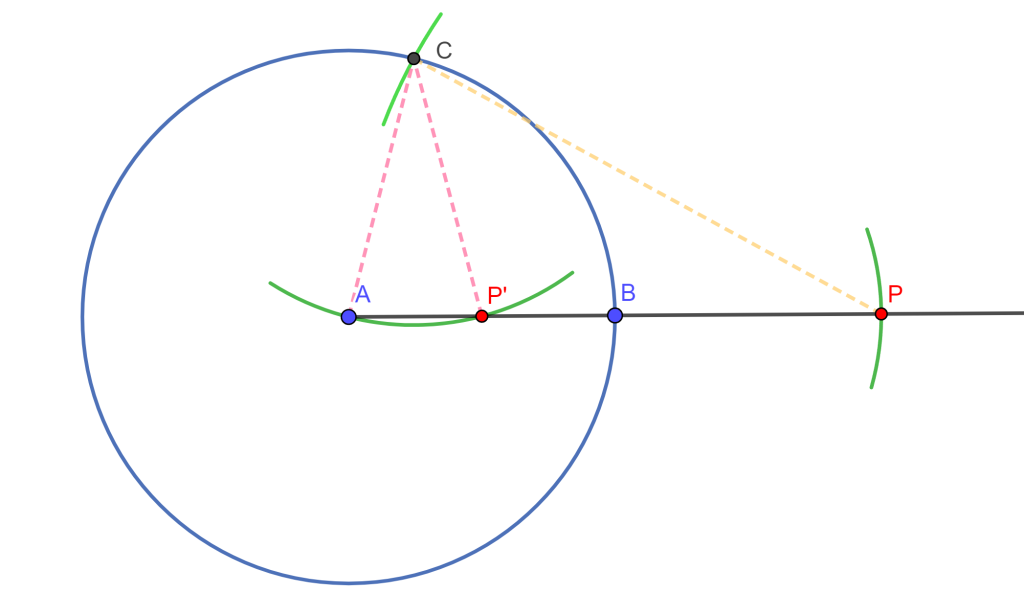
Notemos que $\triangle AP’C \approx \triangle ACP$, ya que son triángulos semejantes isósceles, puesto que comparten un mismo ángulo con vértice $A$, tal que
$\frac{AP’}{AC} = \frac{AC}{AP} \Rightarrow \frac{AP’}{r} = \frac{r}{2r}$
$\Rightarrow AP’= \frac{r \times r}{2r} =\frac{r}{2} =\frac{AB}{2}$
Por lo cual $AP =2r$ y $AP’=\frac{1}{2} r$, entonces $AP \times AP’ =2r \times \frac{1}{2} r =r^2$, esta relación entre $P’$ y $P$ es la que llamamos inversión.
$\square$
La construcción anterior nos sirve para encontrar el inverso, entonces analicemos otras construcciones para encontrar el inverso con compas.
Construcción. Sea $C(O,r)$ y $P$ un punto externo, tracemos la recta $OP$. Ahora con centro $P$ y radio $OP$ dibujamos el arco que interseque a $C(O,r)$ en $Q$. Con centro $Q$ y radio $OQ$, dibujamos un arco que interseque a $OP$ en $P’$.
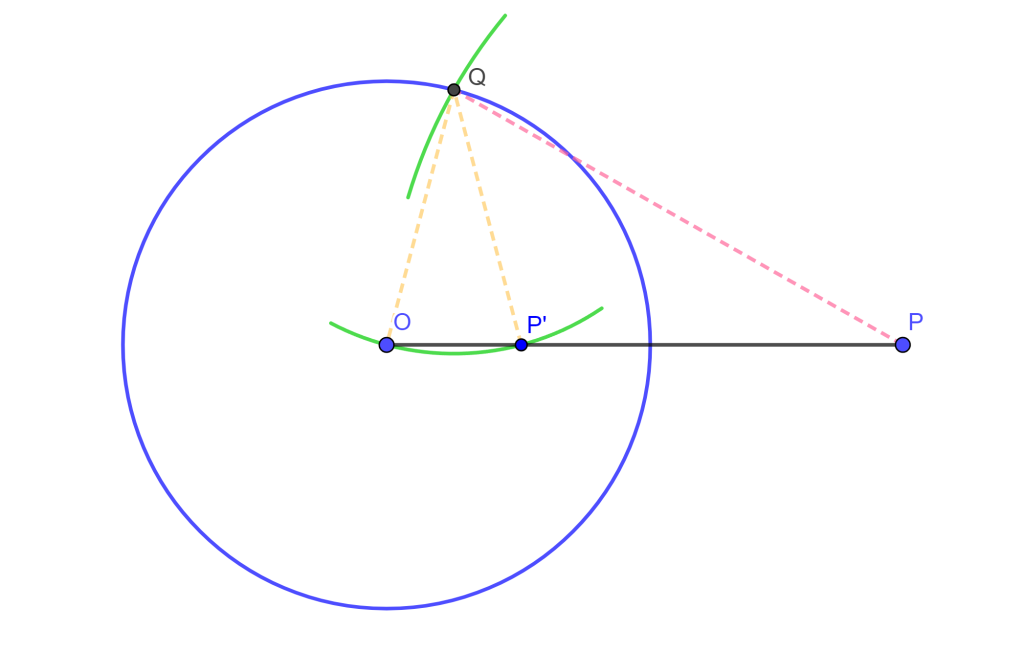
Entonces $P’$ es el inverso de $P$ y como $\triangle OQP \approx \triangle OP’Q$ por triángulos isósceles con ángulo en común $O$ entonces
$\frac{OP}{OQ}=\frac{OQ}{OP’} \Rightarrow OP \times OP’ =r^2.$
$\square$
Construcción. (Método de la tangente) Otra construcción del inverso es de la siguiente forma, dada una circunferencia $C(O,r)$ y un punto $P$ externo a la circunferencia, trazamos el segmento $OP$, y trazamos las tangentes desde $P$ a la circunferencia $C(O,r)$ que son $PQ$ y $PR$ con $Q$ y $R$ los puntos de tangencia, la figura es la siguiente:
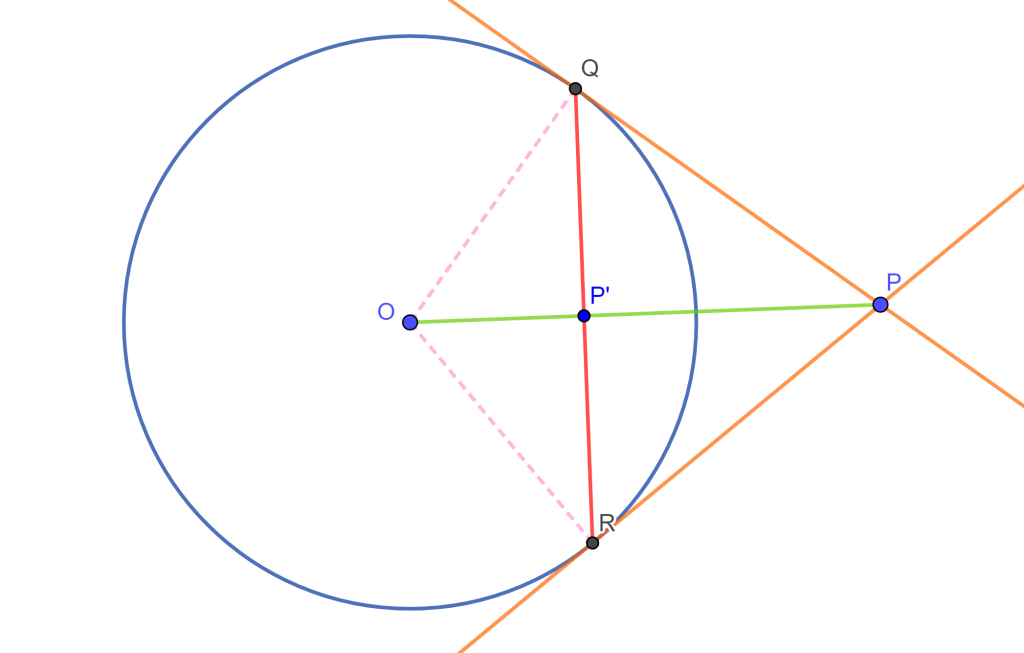
Sea $P’=QR \cap OP$ entonces $P’$ es inverso de $P$.
Sean los $\triangle OQP’$ y $\triangle OPQ$ comparten el angulo $O$, el lado $OQ$ y $\angle OP’Q = \angle OQP$ entonces
$\triangle OQP’ \approx \triangle OPQ \Rightarrow \frac{OP’}{OQ} = \frac{OQ}{OP}$
$\Rightarrow OP’ \times OP = r^2.$
$\square$
Construcción. (Método de la perpendicular) Otro método para ver el inverso cuando $P$ está dentro o fuera de la circunferencia, es de la siguiente forma.
Sea la circunferencia $C(O,r)$ trazamos el diámetro con puntos en los extremos $ST$, donde el diámetro es perpendicular a $OP$. Unimos $S$ con $P$ y la intersección con la circunferencia es $Q$, se une $T$ con $Q$ y esta recta $TQ$ interseca a $OP$ en $P’$, entonces $P’$ es inverso de $P$.
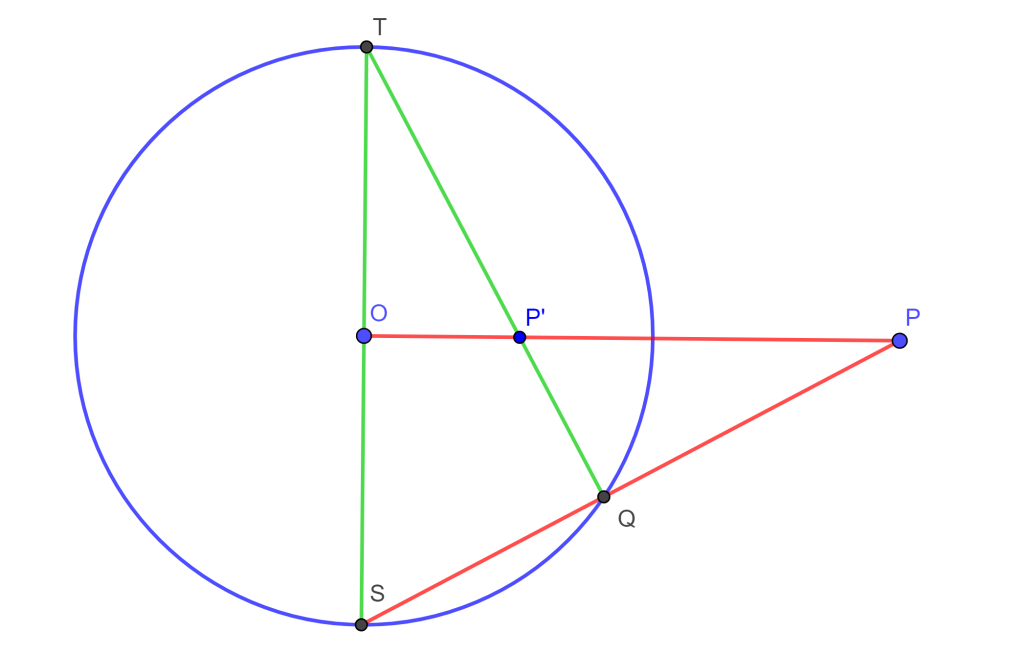
$\square$
Construcción. Dado un punto $P$ fuera de la circunferencia $\alpha$ con centro $O$, construir el inverso de $P$ con respecto a $\alpha$.
Solución. Dibujamos el arco con centro $P$ que pase por $O$ y corte a la circunferencia $\alpha$ en 2 puntos $B$ y $C$; Ahora dibujamos los arcos con centros $B$ y $C$ y que pase por $O$, la intersección la llamaremos $P’$ y será el inverso de $P$.
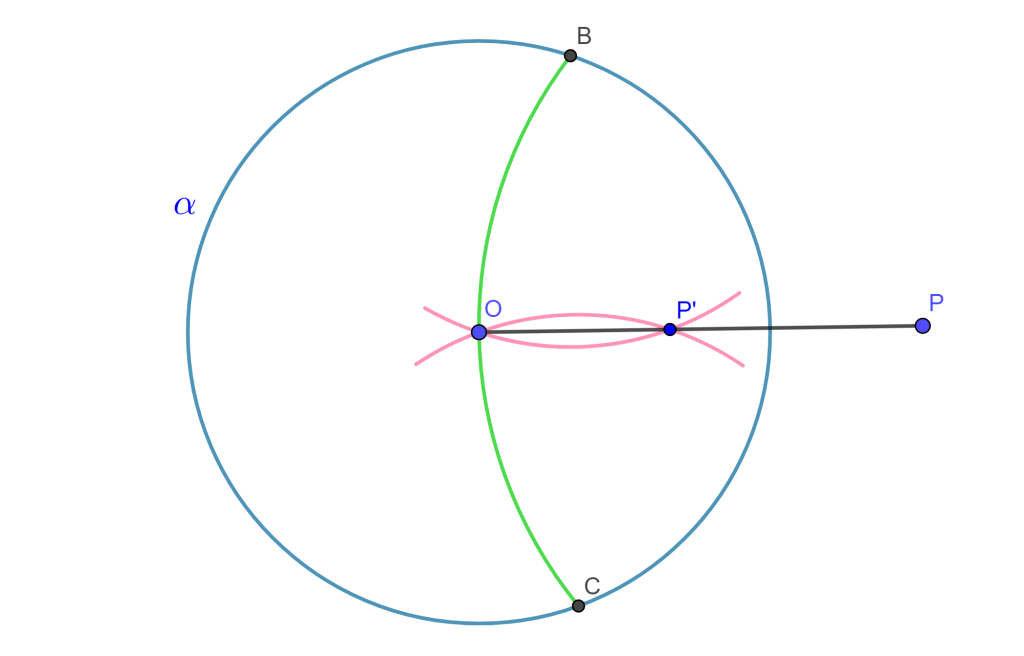
$\square$
Construcción. Dado un punto $A$ y $B$, construir el punto $C$ tal que $B$ es el punto medio de $AC$.
Solución. Trazamos la circunferencia $\alpha$ con centro $B$ y radio $A$, trazamos el arco con centro $A$ y radio $B$ que corte a la circunferencia $\alpha$ en $D$, trazamos el arco con centro $D$ y radio $AB$ que corte a $\alpha $ en $E$ y por último dibujamos el arco con centro $E$ con radio $AB$ que corte a $\alpha$ en $C$.
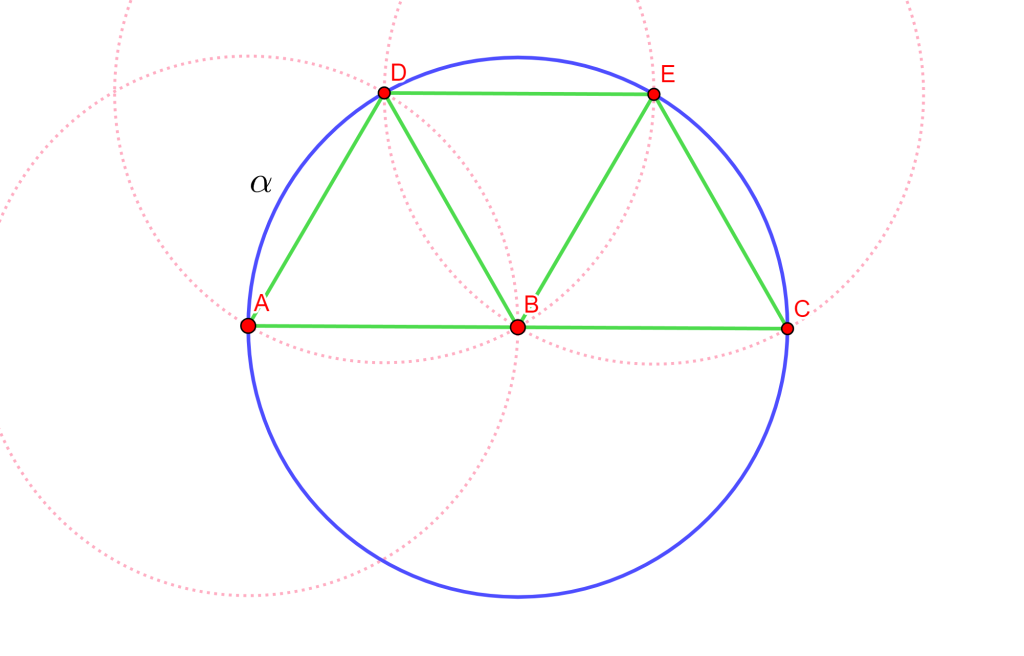
Los triángulos $\triangle ABD$, $\triangle EBC$ y $\triangle DBE$ son equiláteros, entonces $\angle ABD = \angle EBC =\angle DBE = 60°$. Esto significa que $ABC$ es una línea recta, y $AC$ es el diámetro de$\alpha$.
Por lo tanto, $B$ es el punto medio de $AC$.
$\square$
Construcción. Dada una circunferencia $\alpha$ con centro $A$ y radio $r$, y dado un punto $P$ dentro de $\alpha$, construir el inverso de $P$ con respecto a $\alpha$.
Solución. Para esta se usarán distintas construcciones, es por ello que usando la construcción 5 se pueden construir puntos $P_1$, $P_2$, $P_3$,…, $P_i$ tal que $P_i$ este fuera de $\alpha$, entonces:
$ \begin{split} AP_1 &= 2AP \\ AP_2 &= 2AP_1 = 4AP \\ AP_3 &= 2AP_2 =8AP \\ &. \\ &. \\ &. \\ AP_i &= 2AP_{i-1} =2^iAP \end{split} $
Si $k=3$ entonces
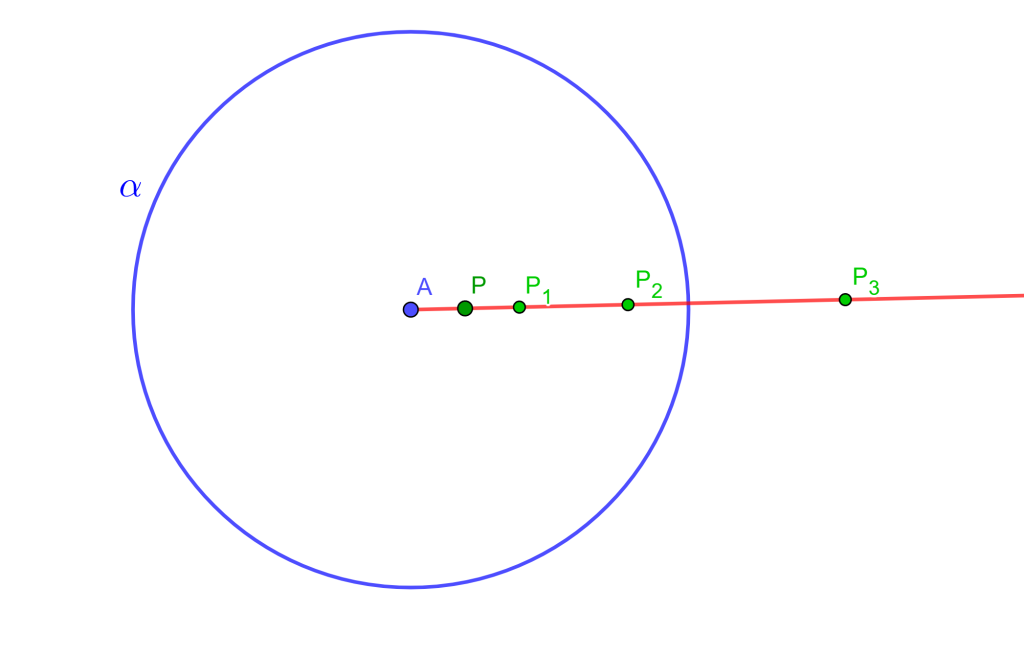
Usando la construcción 4 se puede encontrar el inverso de $P_i$ lo llamaremos $S$, entonces $AS \times AP_i =r^2$. De igual forma, aplicando la construcción 5 a $S$ se pueden generar puntos $S_1$, $S_2$,…, $S_i$ tal que
$ \begin{split} AS_1 &= 2AS \\ AS_2 &= 2AS_1 = 4AS \\ AS_3 &= 2AS_2 =8AS \\ &. \\ &. \\ &. \\ AS_i &= 2AS_{i-1} =2^iAS \end{split} $
Entonces $S_i$ es el inverso de $P$, por lo cual
$AS_i \times AP = 2^i AS \times AP= AS \times 2^i AP =AS \times AP_i =r^2.$
$\square$
Construcción. Dada una circunferencia $\alpha$ con centro desconocido $A$, construir este centro.
Solución. Con un punto $P$ en $\alpha$, construimos un círculo $\omega$ que interseca a $\alpha$ en $C$ y $D$, radio de $\omega $ es menor al radio de $\alpha$. Dibujar los arcos de $C$ y $D$ con radio $CP$ y se intercepta en $Q$. Y por la construcción 6 se encuentra $Q’$ el inverso de $Q$ con respecto a $\omega$, por lo tanto, $Q’$ es el centro de $\alpha$ y $Q’=A$.
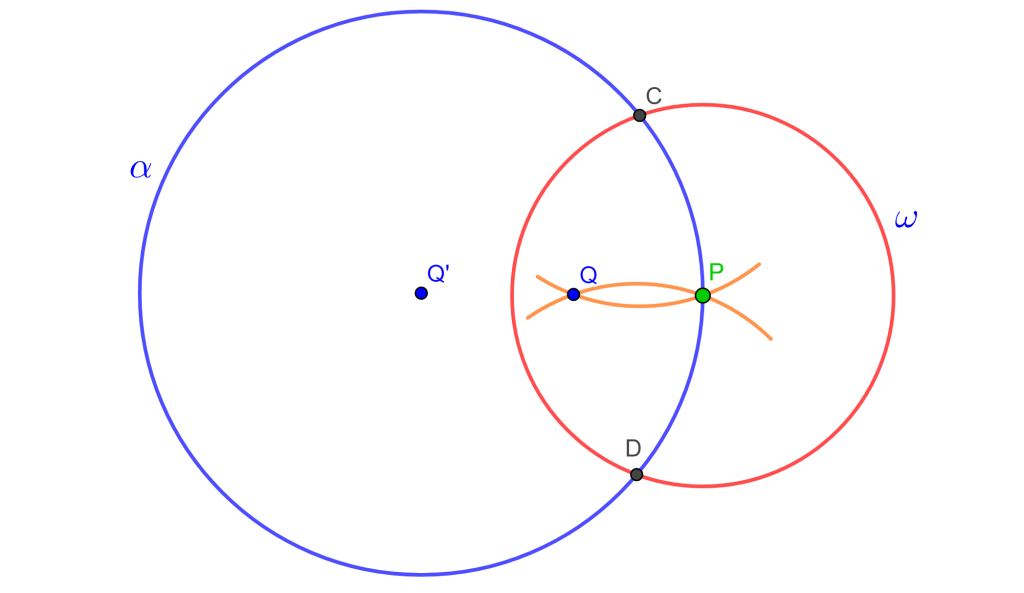
$\square$
Más adelante…
Con esto concluye la unidad de Inversión, es por ello que ahora es necesario dejar algunos problemas para reforzar e investigar más sobre la Inversión.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Inversión de un Teorema y circunferencia de antisimilitud
- Siguiente entrada del curso: Ejercicios Unidad 2 Inversión
