Introducción

Definición. Si C es un arco de curva rectificable, definimos su longitud $L(C)$ como la suma
$$\boxed{L_{C}=\sup{s(P)}=\sup\left\{\Sigma\|f(t_{k})-f(t_{k-1})\|\right\}}$$
Ahora vamos a obtener una fórmula para la longitud de arco.
Sea $\overline{\alpha}:[a,b]\rightarrow \mathbb{R}^{2}$ ó $\mathbb{R}^{3}$, continua en $[a,b]$, derivable en (a,b) y $\overline{\alpha^{\prime}}(t)\neq 0$ para todo $t\in [a,b]$ y sea $P={t_{0},t_{1},…,t_{n}}$ una partición de $[a,b]$

entonces según la figura se tiene que
$$\ell(\overline{\alpha})\approx \sum_{i=1}^{n}\|\alpha(t_{i})-\alpha(t_{i-1})\|=\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}(t_{i})-\alpha_{1}(t_{i-1})\right]^{2}+…+\left[\alpha_{n}(t_{i})-\alpha_{n}(t_{i-1})\right]^{2}}$$
Aplicando el teorema del valor medio en cada subintervalo $[t_{i-1},t_{i}]$ tenemos que
$$\frac{\alpha_{i}(t_{i})-\alpha_{i}(t_{i-1})}{t_{i}-t_{i-1}}=\alpha^{\prime}(t^*),~~~t^*\in(t_{i-1},t_{i})$$
se tiene que
\begin{align*}&\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}(t_{i})-\alpha_{1}(t_{i-1})\right]^{2}+…+\left[\alpha_{n}(t_{i})-\alpha_{n}(t_{i-1})\right]^{2}}=\\&\sum_{i=1}^{n}\sqrt{\left[\alpha_{1}^{\prime}(t_{1})(t_{i}-t_{i-1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})(t_{i}-t_{i-1})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t_{1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t_{1})\right]^{2}+…+\left[\alpha_{n}^{\prime}(t_{n})\right]^{2}}=\\&\sum_{i=1}^{n}(t_{i}-t_{i-1})\sqrt{\left[\alpha_{1}^{\prime}(t)\right]^{2}+…+\left[\alpha_{n}^{\prime}(t)\right]^{2}}=\\&\sum_{i=1}^{n}\|\alpha^{\prime}(t^*)\|(t_{i}-t_{i-1})\\&Si~{n\rightarrow \infty}~~entonces~~\sum_{i=1}^{n}\|\alpha^{\prime}(t^*)\|(t_{i}-t_{i-1})\rightarrow \int_{a}^{b}\|\alpha^{\prime}(t)\|~dt\end{align*}
Definición. Sea $f:I\subset \mathbb{R}\rightarrow \mathbb{R}^{2}$ ó $\mathbb{R}^{3}$ una curva parametrizable. Sean $a,b\in I$ con $a<b$. Para cualquier partición $P={t_{0},…,t_{n}}$ del intervalo $[a,b]$ definimos
$$sup\left\{\sum_{i=1}^{n}\|\alpha^{\prime}(t)\|(t_{i}-t_{i-1})\right\}=\int_{a}^{b}\|\alpha^{\prime}(t)\|~dt$$
curva o la longitud de arco de la curva en caso de que la integral exista.
Ejemplo. Calcular la longitud de arco de $\sigma(t)=(rt-r\sin(t),r-r\cos(t))$. En este caso
tenemos que $\sigma^{\prime}=(r-r\cos(t),r\sin(t))$ para $t\in[0,2\pi]$ $\therefore$ la longitud de arco es:
\begin{align*} \int_{0}^{2\pi}\sqrt{(r-r\cos(t))^{2}+(r\sin(t))^{2}} &=\int_{0}^{2\pi}\sqrt{r^{2}-2r^{2}\cos(t)+r^{2}\cos^{2}(t)+r^{2}\sin^{2}(t)}dt \\ &=\int_{0}^{2\pi}\sqrt{2r^{2}-2r^{2}\cos(t)}dt \\ &=\sqrt{2}r\int_{0}^{2\pi}\sqrt{1-\cos(t)}dt\\ &=\sqrt{2}r\int_{0}^{2\pi}\sqrt{2}\sin\left(\frac{t}{2}\right)dt\\&=2r\int_{0}^{2\pi}\sin\left(\frac{t}{2}\right)dt \\ &=2r\left(2\cdot\left(-\cos\left(\frac{t}{2}\right)\right|_{0}^{2\pi}\right) \\ &=8r.~ \blacksquare \end{align*}

Reparametrización de curvas

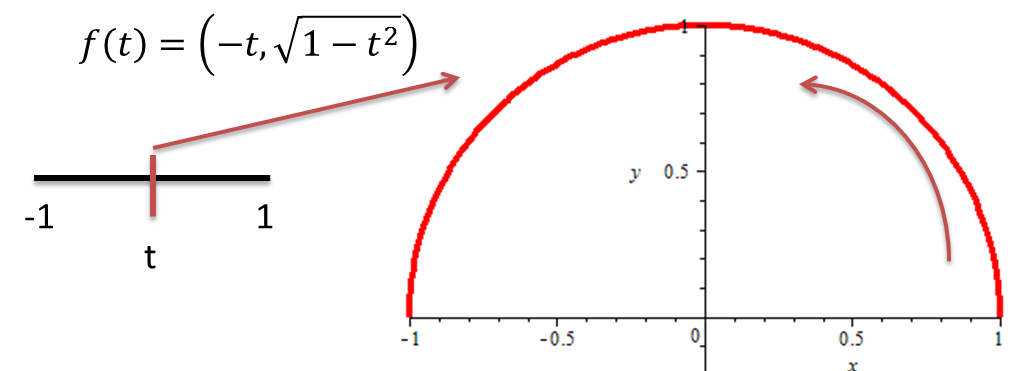
Consideremos la curva $f:[-1,1]\rightarrow \mathbb{R}^{2}$
dada por $f(t)=(-t,\sqrt{1-t^{2}})$ la cual describe un arco de la
circunferencia $x^{2}+y^{2}=1$ entre -1 y 1.

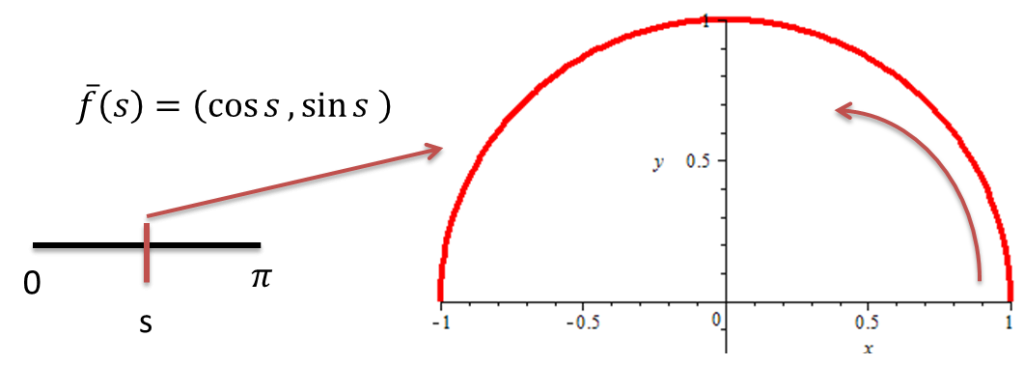
Sea $\overline{f}:[0,\pi]\rightarrow[0,1]$ la función $\overline{f}(s)=[\cos(s),\sin(s)]$

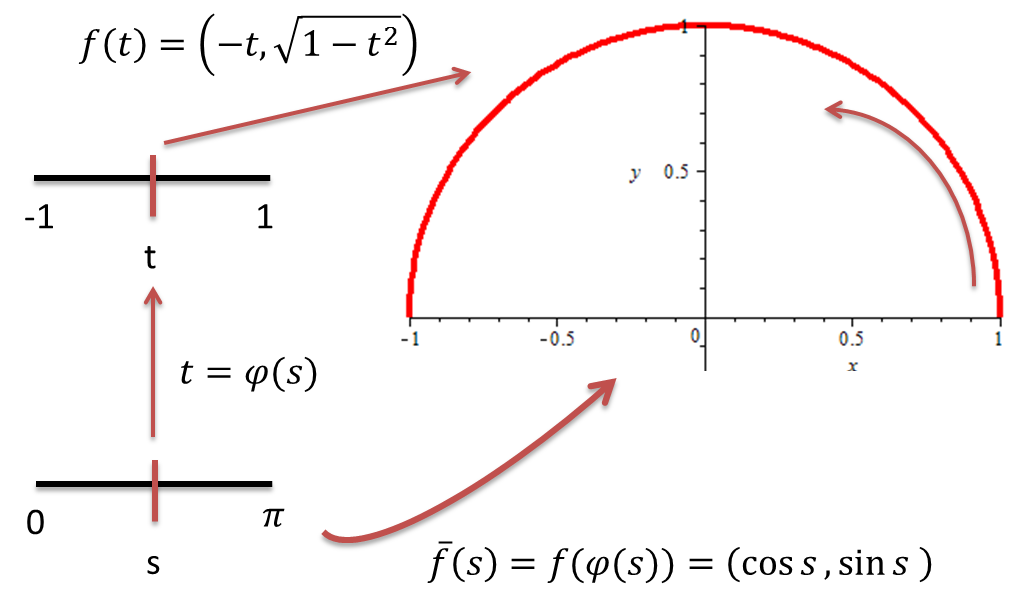
Si definimos una función $\varphi:[0,\pi]\rightarrow[-1,1]$ dada por $\varphi(s)=-cos(s)$ tenemos que $\overline{f}=f\circ\varphi$, es decir
$$\overline{f}(s)=f\circ \varphi(s)=f(\varphi(s))=f(-cos(s))=[-(-cos(s)),\sqrt{1-(-\cos(s))^{2}}]=[cos(s),\sin(s)]$$

Decimos que $\overline{f}$ es una reparametrización de $f$.$~~\blacksquare$
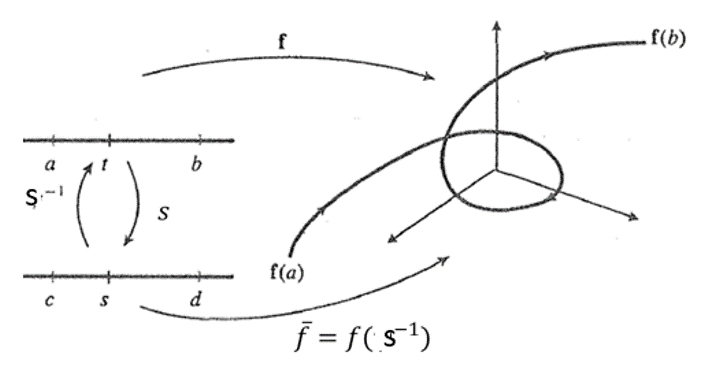
Definición. Sea $f:[a,b]\subset\mathbb{R}^{n}$ una curva con derivada distinta de cero. Sea $\varphi:[c,d]\rightarrow[a,b]$ una función con derivada continua sobreyectiva tal que $\varphi’\neq0$ $\forall s\in [a,b]$. Entonces la curva $\overline{f}=f\circ\varphi:[c,d]\rightarrow\mathbb{R}^{n}$ se llama reparametrización de la curva f.
Nota:
La condición $\varphi’\neq0$ nos conduce a $\varphi’>0$ o $\varphi'<0$. Si $\varphi’>0$ entonces $\varphi$ es una función creciente en [c,d] de modo que $\varphi(c)=a$ y $\varphi(d)=b$ y asi los puntos inicial y final de $\overline{f}$ coinciden con los respectivos de f$$\overline{f}(c)=f\circ\varphi(c)=f(\varphi(c))=f(a)~~~y~~~ \overline{f}(d)=f\circ\varphi(d)=f(\varphi(d))=f(b)$$
como $\overline{f}'(s)=\varphi'(s)f'(\varphi(s))$ entonces $f’$ y $\overline{f}’$ tienen la misma dirección y en este caso como $\varphi’~>0$, entonces, el camino en el que $\overline{f}$ recorre la curva descrita por f es en la misma dirección. Por lo tanto diremos que $\overline{f}$ es una reparametrización de f que conserva la orientación.
Ejemplo. Obtenga una reparametrización de la curva $f:[0,2]\rightarrow\mathbb{R}^{2}$ dada por $f(t)=(3t+2,t^{3}+3)$.
Solución. Proponemos la función $t=\varphi(s)=2s$, en la cual se tiene $\varphi'(s)=2>0$,
es decir si su derivada es constante, entonces no se anula para ningun valor. Ahora bien si $t=0\Rightarrow s=0$ y $t=2\Rightarrow s=1$ por lo tanto $\varphi:[0,1]\rightarrow[0,2]$ mientras que
$$\overline{f}(s)=f(\varphi(s))=f(2s)=(3(2s)+2,(2s)^{3}+3)=(6s+2,8s^{3}+3)\quad
s\in[0,1]$$ tenemos entonces que $\overline{f}$ es una reparametrización de f. Vamos a comprobar que representan el mismo lugar geométrico. Para $f(t)$ se tiene $\displaystyle{x=3t+2\rightarrow t=\frac{x-2}{3}}$ y si $y=t^{3}+3$ entonces $\displaystyle{y=\left(\frac{x-2}{3}\right)^{3}+3}$ mientras que para $\overline{f}(s)$, $\displaystyle{x=6s+2\rightarrow s=\frac{x-2}{6}}$ por tanto si $y=8s^{3}+3$ entonces $\displaystyle{y=8\left(\frac{x-2}{6}\right)^{3}+3}$ por lo que igualando coordenadas de cada representación paramétrica, se tiene$$\left(\frac{x-2}{3}\right)^{3}+3=8\left(\frac{x-2}{6}\right)^{3}+3\Rightarrow \frac{1}{3^{3}}=\frac{8}{6^{3}}$$ lo cual es cierto y por lo tanto representan el mismo lugar geometrico.$~~\blacksquare$
Proposición. Supongamos que $f:[a,b]\rightarrow\mathbb{R}^{n}$ es una curva con $f’\neq 0$ y que $\overline{f}:[c,d]\rightarrow\mathbb{R}^{n}$ es una reparametrización de f. Entonces
$$\int_{a}^{b}\|f'(t)\|~dt=\int_{c}^{d}\|\overline{f}'(s)\|~ds$$
Demostración. Tenemos que $\overline{f}=f\circ \varphi$, donde $\varphi:[c,d]\rightarrow[a,b]$ es de clase $c^{1}$, biyectiva y $\varphi’\neq 0~~\forall~s\in [c,d]$. Entonces
\begin{align*} L(\overline{f}) &=\int_{c}^{d}|\overline{f}'(s)|~ds \\ &=\int_{c}^{d}\|\varphi'(s)f'(\varphi(s))\|~ds \\ &=\int_{c}^{d}\|\overline{f}'(\varphi(s))\|~|\varphi'(s)|~ds~~~(si~\varphi’>0)\\
&=\int_{c}^{d}\|\overline{f}'(\varphi(s))\|~\varphi'(s)~ds \\
&=\int_{a}^{b}\|f'(t)\|~dt,~~(t=\varphi(s),~~dt=\varphi'(s)~ds) \\
&=L(f).~~ \blacksquare \end{align*}

Función Longitud de Arco

A continuación introducimos la función longitud de arco de una curva. Esta función nos permitirá prporcionar una nueva reparametrización de una curva, lo cual será de gran
utilidad más adelante.
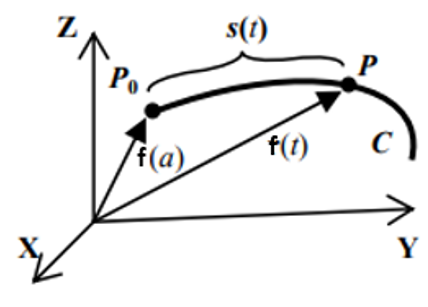
Definición. Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva de longitud L. Se llama función longitud de arco de la curva $f(t)$ a la función $s:[a,b]\rightarrow[0,L]$ dada por
$$s(t)=\int_{a}^{t}\|f'(u)\|~du$$
$s(t)$ es la longitud del arco entre los puntos $P_{0}$ y $P$, que son los puntos terminales de $f(a)$ y $f(t)$

Ejemplo. Hallar la función longitud de arco de la hélice $f(t)=(\cos(t),\sin(t),t),~~t\in[0,2\pi]$.
Solución. En este caso tenemos que
\begin{align*} f'(t) & =(-\sin(t),\cos(t),1) \\ |f'(t)| & =\sqrt{(-\sin(t))^{2}+(\cos(t))^{2}+1^{2}}=\sqrt{2} \end{align*}
Ahora, para $t\in[0,2\pi]$ tenemos
$$s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}\sqrt{2}~du=\sqrt{2}t$$
Si $t\in[0,2\pi]$ entonces
\begin{align*} s(0)&=0\\s(2\pi)&=2\pi\sqrt{2}\end{align*}
Luego, la función longitud de arco $s:[0,2\pi]\rightarrow[0,2\pi\sqrt{2}]$ de esta porción de hélice es
$$s(t)=\sqrt{2}t.~~ \blacksquare$$

Reparametrización por Longitud de Arco

Entre las muchas reparametrizaciones de una curva contamos con una que está muy relacionada con las características geométricas de la curva y además, posee propiedades importantes. Esta es la reparametrización por longitud de arco, la que se obtiene mediante la función de longitud de arco.
Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva diferenciable. Para reparametrizarla por longitud de arco se siguen los siguientes pasos:
(a) Hallar la función longitud de arco de la curva:
$$s:[a,b]\rightarrow[0,L],~~~\displaystyle{s(t)=\int_{a}^{t}\|f'(u)\|~du}$$
(b) Hallar la función inversa de la función longitud de arco:
$$\varphi=s^{-1}:[0,L]\rightarrow[a,b]$$
La reparametrización por longitud de arco de la curva $f:[a,b]\rightarrow\mathbb{R}^{n}$ es
$$\overline{f}=f\circ \varphi:[0,L]\rightarrow\mathbb{R}^{n}$$
Ejemplo. Sea $f(t)=(r \cos t , r\sin t)$ con $t\in[0,2\pi]$. Obtengamos su reparametrizacion por longitud de arco.
Solución.
(a) Hallamos la función longitud de arco s(t) que en éste caso es:
$$f'(t)=(-r\sin(t),r\cos(t))~~y~~\|f'(t)\|=\sqrt{(-r\sin(t))^{2}+(r\cos(t))^{2}}=r$$
$s:[0,2\pi]\rightarrow[0,2\pi r]$, $\displaystyle{s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}r~du=rt}$ esto es
$$s(t)=rt$$
Si $t\in[0,2\pi]$ entonces
\begin{align*}s(0)&=0\\s(2\pi)&=2\pi r\end{align*}
Por lo que $s\in[0,2\pi r]$
(b) Hallamos la función inversa de la longitud de arco
$$\varphi=s^{-1}:[0,2\pi r]\rightarrow[0,2\pi]$$
Sea $s=s(t)$. Entonces $s=rt$, por lo tanto despejando t tenemos $\displaystyle{t=\frac{s}{r}}$. Luego
$$t=\varphi(s)=s^{-1}=\frac{s}{r}$$
Por lo tanto la reparametrización buscada es
$$\overline{f}(s)=f\circ \varphi(s)=f\left(\varphi(s)\right)=f\left(\frac{s}{r}\right)=\left(r\cos
\left(\frac{s}{r}\right),r\sin\left(\frac{s}{r}\right)\right)~~\blacksquare$$
Observación.
En el ejemplo anterior notamos que:
$$\|\overline{f}^{\prime}(s)\|=
\left\|-r\sin\left(\frac{s}{r}\right)\frac{1}{r},r\cos \left(\frac{s}{r}\right)\frac{1}{r}\right\|=
\left\|-\sin\left(\frac{s}{r}\right),\cos\left(\frac{s}{r}\right)\right\|=1$$

Ejemplo. Sea $f(t)=(\cos t , \sin t,t),~~t\in[0,2\pi]$ . Obtengamos la reparametrizacion por la longitud de arco.
Solución.
(a) Hallamos la función longitud de arco s(t), que en éste caso es:
$$f'(t)=(-\sin(t),\cos(t),1)~~y~~\|f'(t)\|=\sqrt{(\sin(t))^{2}+(\cos(t))^{2}+1^{2}}=\sqrt{2}$$
Si $t\in[0,2\pi]$ entonces $s:[0,2\pi]\rightarrow[0,2\pi \sqrt{2}]$, por lo que$\displaystyle{s(t)=\int_{0}^{t}\|f'(u)\|~du=\int_{0}^{t}\sqrt{2}~du=\sqrt{2}t}$ esto es
$$s(t)=\sqrt{2}t$$
Hallamos la función inversa de la longitud de arco
$$\varphi=s^{-1}:[0,2\pi \sqrt{2}]\rightarrow[0,2\pi]$$
Sea $s=s(t)$. Entonces $s=\sqrt{2}t$, por lo tanto despejando t tenemos $\displaystyle{t=\frac{s}{\sqrt{2}}}$. Luego
$$t=\varphi(s)=s^{-1}=\frac{s}{\sqrt{2}}$$
y la reparametrización buscada es
$$\overline{f}(s)=f\circ h(s)=f\left(h(s)\right)=f\left(\frac{s}{\sqrt{2}}\right)=\left(r\cos
\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right),~~s\in[0,2\pi \sqrt{2}] \blacksquare$$

La reparametrización por longitud de arco tiene rapidez constante

Sabemos que si $\textbf{s}:[a,b]\rightarrow [c,d]$ es una función de clase $c^{1}$ tal que $\textbf{s}’\neq 0~~\forall~t\in[a,b]$, también se tiene $\textbf{s}^{-1}:[c,d]\rightarrow [a,b]$ es tal que $(\textbf{s}^{-1})’$ es de clase $c^{1}$.
Observamos que la función $\varphi=\textbf{s}^{-1}:[c,d]\rightarrow [a,b]$ tiene entonces las características que se necesitan para que $\overline{f}=f\circ \varphi$ sea una reparametrización de f.

Tenemos que para $s\in [c,d]$
$$\overline{f}(s)=(f\circ\varphi)(s)=f(\varphi(s))$$
por lo que
$$\overline{f}'(s)=(f\circ\varphi)'(s)=f'(\varphi(s))\varphi'(s)$$
Pero
$$\varphi'(s)=(\textbf{s}^{-1})'(s)=\frac{1}{\textbf{s}'(\textbf{s}^{-1}(s))}=\frac{1}{\textbf{s}'(\varphi(s))}=\frac{1}{\|f'(\varphi(s))\|}$$
Por lo tanto
$$\|\overline{f}'(s)\|=\|f'(\varphi(s))\varphi'(s)\|=\left\|f'(\varphi(s))\cdot\frac{1}{\|f'(\varphi(s))\|} \right\|=\|f'(\varphi(s))\|\cdot\frac{1}{\|f'(\varphi(s))\|}=1~~ \blacksquare$$

Propiedad de la reparametrización por longitud constante

Si $\overline{f}$ es una reparametrización de f tal que $\|\overline{f}(t)\|=1$ para toda $t\in [a,b]$ entonces
$$L(\overline{f})=\int_{a}^{b}\|\overline{f}(t)\|~dt=\int_{a}^{b}~dt=b-a$$
Por lo que $\overline{f}$ es una reparametrización tal que la longitud que describe es igual al tiempo que tarda en recorrerla.$~\blacksquare$

Más adelante

Tarea Moral

1.- Aporta una parametrización al cuadrado unitario de $\mathbb{R}^2$ con vértices en los puntos: (0,0), (1,0), (1,1), (0,1).

2.- Determina la longitud de arco de la parábola descrita por $f(t)=(t^2,2t)$, $t\in [0,1]$

3.- Determina la longitud de la gráfica de $y=ln(1-x^2)$ entre $x=0$ y $x=\dfrac{1}{2}$

4.- La gráfica polar de $r=1+cos\theta$ es una cardioide y sus ecuaciones paramétricas son: $x=(1+cos\theta)cos\theta$, $y=(1+cos\theta) sen\theta $, $\theta \in [0,2\pi]$. Determina su longitud de arco.

5.- Encuentra una reparametrización de la elipse $r(t)=(acost, bsent)$, $t\in [0,2\pi]$ y determina su reparametrización por longitud de arco.