Introducción

En tu formación matemática muchas veces te encontrarás con resultados de clasificación. Pero, ¿qué es clasificar en este contexto? A grandes rasgos, consiste en poder decir de manera sencilla cómo son todos los objetos matemáticos que se estén estudiando en un contexto dado.

En esta entrada hablaremos un poco más del problema de clasificar ciertos objetos matemáticos. Iniciaremos con un ejemplo «de juguete» muy básico. Luego, hablaremos de cómo en las clasificaciones geométricas podemos usar transformaciones. Finalmente, daremos un ejemplo sencillo de cómo usar estas ideas en la clasificación de los segmentos del plano.

Ejemplo básico de clasificación

Cuando queremos hacer una clasificación, en el sentido matemático, lo que queremos hacer es tomar algunos objetos matemáticos y decir, bajo algún criterio cómo son todos los «tipos posibles» que existen para esos objetos. Esto puede ser respondido de muchas formas, así que es fundamental acordar dos cosas con precisión:

1. ¿Cuáles son los objetos que queremos clasificar?
2. ¿Bajo qué criterio diremos que dos de esos objetos son «del mismo tipo»?

Al final del proceso, nos gustaría tener una lista relativamente fácil de escribir de todas las posibilidades. Esto puede ayudar posteriormente a resolver otros problemas matemáticos o bien a desarrollar más teoría.

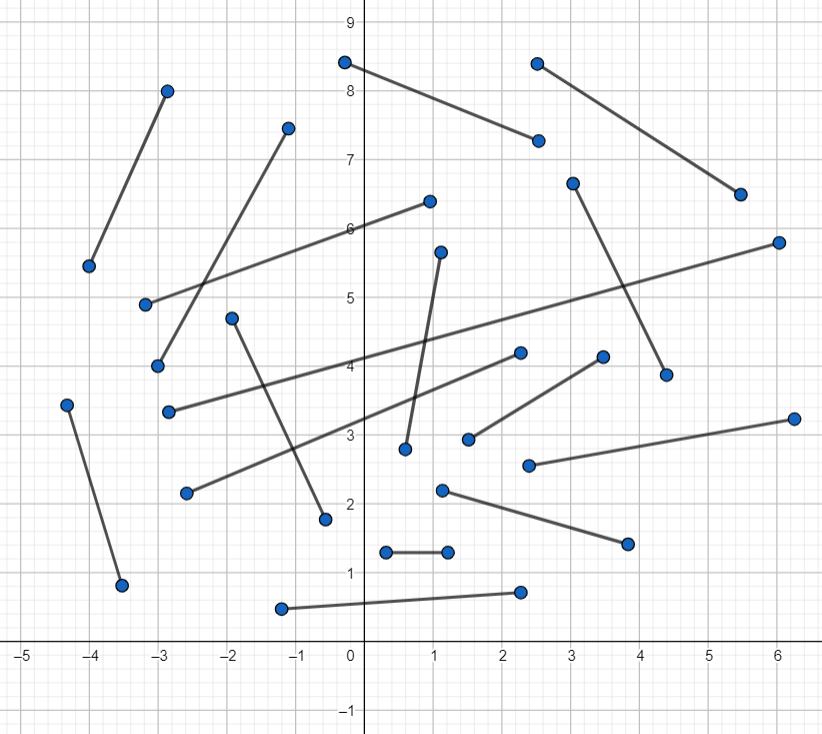
Comencemos con un ejemplo «de juguete». Será muy sencillo, pero nos permitirá hablar de algunas de las sutilezas que nos encontraremos en contextos más abstractos. Considera la siguiente figura en la que hay varias figuras geométricas.

Imagina que nos piden «clasificar todas las figuras que están aquí». Lo que nos gustaría obtener al final es una lista con la clasificación, es decir con «todas las posibilidades» de figuras que hay. Si sólo nos dan esta instrucción, entonces estaríamos en problemas: hay muchas formas de clasificar estos objetos.

Una posible clasificación es por forma. Si consideramos equivalentes a dos de estas figuras cuando tienen la misma forma, entonces nuestra lista de posibilidades se reduce a tres: triángulos, cuadrados y círculos. Nuestro teorema de clasificación se vería así:

Teorema. Cualquier figura de la imagen tiene alguna de las siguientes formas:

1. Triángulo
2. Cuadrado
3. Círculo

Este teorema de clasificación está padre. Pero puede ser inútil en algunos contextos. Por ejemplo, imagina que las figuras son muestras que está regalando una tienda de pinturas para que puedas llevarlas a tu casa y usarlas para ver si te gustaría pintar una pared con el color dado. Para estos fines es (prácticamente) lo mismo que te den un cuadrado azul o un triángulo azul. Lo único que importa es el color.

Pensar de esta manera nos da otra manera de clasificar a las figuras: por color. Si usamos esta noción de equivalencia, entonces nuestro resultado de clasificación sería muy distinto.

Teorema. Cualquier figura de la imagen es de alguno de los siguientes colores:

1. Rojo
2. Naranja
3. Amarillo
4. Verde
5. Azul

Pero podríamos querer ser mucho más estrictos y querer clasificar considerando ambos criterios: tanto la forma como el color. Quizás uno podría pensar que como hay tres figuras y cinco colores, entonces hay $3\cdot 5=15$ posibilidades en esta clasificación. Obtendríamos el siguiente resultado.

Teorema. Cualquier figura de la imagen es de alguno de los siguientes 15 tipos: triángulo rojo, triángulo naranja, triángulo amarillo, triángulo verde, triángulo azul, cuadrado rojo, cuadrado naranja, cuadrado amarillo, cuadrado verde, cuadrado azul, círculo rojo, círculo naranja, círculo amarillo, círculo verde, círculo azul.

Estrictamente hablando, este resultado es correcto: cualquier figura es de alguno de esos tipos. Pero el teorema tiene algo incómodo: nos está dando posibilidades que no suceden. Por ejemplo, no hay cuadrados amarillos, ni círculos azules.

Una clasificación con forma y color que nos dejaría más satisfecho sería la siguiente:

Teorema. Cualquier figura de la imagen es de alguno de los siguientes 11 tipos:

1. Triángulo rojo
2. Triángulo naranja
3. Triángulo amarillo
4. Triángulo azul
5. Cuadrado rojo
6. Cuadrado naranja
7. Cuadrado azul
8. Círculo rojo
9. Círculo naranja
10. Círculo amarillo
11. Círculo verde

Más aún, cualquiera de estas posibilidades sucede.

Este resultado se siente mucho más satisfactorio. Por un lado, no está agregando a la lista «opciones de más». Por otro lado, a partir de él podemos demostrar proposiciones sin tener que volver a ver la figura. Algunos ejemplos son los siguientes:

• Ningún círculo de nuestra figuras es azul.
• Todas las figuras verdes son círculos.
• Ninguna figura amarilla es un cuadrado.

Para mostrar cualquiera de estas, basta ver nuestra clasificación.

¿Podemos dar una clasificación mucho más estricta? Sí, por supuesto. Por ejemplo, podemos considerar dos figuras iguales sólo cuando tienen exactamente la misma figura, color y posición. En este caso nuestro teorema de clasificación tendría un tipo por cada una de las 19 figuras. Esta clasificación también se siente un poco insatisfactoria pues en realidad no estamos «agrupando» figuras, sino simplemente «poniendo a cada una en su propio grupo». Pero bueno, es una clasificación válida también.

Uso de relaciones de equivalencia y particiones

Una manera de formalizar una clasificación es a partir de relaciones de equivalencia y particiones. Recordemos las siguientes dos definiciones:

Definición. Una relación de equivalencia en un conjunto $X$ es una colección de parejas $(x,y)$ en $X\times X$ tales que:

• (Reflexividad) Para cualquier $x$ en $X$ la pareja $(x,x)$ está en la colección.
• (Simetría) Si para algunos $x,y$ en $X$ se cumple que la pareja $(x,y)$ está en la colección, entonces la pareja $(y,x)$ también está en la colección.
• (Transitividad) Si para algunos $x,y,z$ en $X$ se cumple que tanto las parejas $(x,y)$ como $(y,z)$ están en la colección, entonces la pareja $(x,z)$ también está.

Las relaciones de equivalencia nos ayudan a decir cuándo dos objetos de $X$ «son iguales» o «son el mismo» bajo algún criterio usualmente más relajado que la igualdad.

Definición. Una partición de un conjunto $X$ es una colección de conjuntos $(A_i)_{i \in I}$ para algún conjunto de índices $I$ tal que ninguno de los $A_i$ es vacío, cualesquiera dos de ellos tienen intersección vacía y $X=\cup_{i\in I}A_i$.

Un resultado clásico de teoría de conjuntos dice que «una relación de equivalencia da una partición, y viceversa». Formalmente, dada una relación de equivalencia $R$ en un conjunto $X$, podemos crear la clase de equivalencia de un elemento $x$ en $X$ como sigue: $$\overline(x):=\{y \in X: (x,y)\in R\}.$$ El conjunto $\{\overline{x}:x\in X\}$ da una colección de conjuntos que es una partición de $X$. Y viceversa, si tenemos una partición $(A_i)_{i \in I}$, entonces podemos considerar las parejas $(x,y)$ de elementos tales que $x$ y $y$ están en un mismo $A_i$, de donde obtenemos una relación de equivalencia.

Regresando a la idea de clasificar, podemos realizar una clasificación a través de una relación de equivalencia o de una partición. Las clases de equivalencia son los «tipos» de objetos que tenemos. Podemos dar un representante «sencillo» dentro de cada clase de equivalencia para hacer nuestra lista de los posibles «tipos» que existen.

Ejemplo. En los números enteros podemos decir que dos enteros $x$ y $y$ están relacionados cuando $x-y$ es un número par. Es fácil mostrar que esto da una relación de equivalencia y que las clases de equivalencia en este caso son los conjuntos:

\begin{align*}
P&=\{\ldots,-4,-2,0,2,4,\ldots\},
Q&=\{\ldots,-3,-1,1,3,\ldots\}.
\end{align*}

Tenemos que $P$ y $Q$ forman una partición del conjunto $\mathbb{Z}$ de números enteros. Así, esta relación clasifica a los enteros en dos tipos: los pares y los impares. Otra forma de dar esta clasificación es diciendo que «Cualquier entero es equivalente al $0$ o al $1$», o más explícitamente, «Para cualquier entero $z$ se tiene que o bien $z$ es par, o bien $z-1$ es par».

$\triangle$

Clasificación de segmentos del plano con transformaciones

Hacia donde queremos ir es hacia una clasificación relacionada con la geometría. Por esta razón, las relaciones de equivalencia, particiones o «tipos» de objetos que obtendremos estarán relacionados con nociones geométricas. Una manera de hacer esto es mediante las transformaciones que estuvimos estudiando en la unidad anterior: transformaciones afines, traslaciones, isometrías, transformaciones ortogonales, etc.

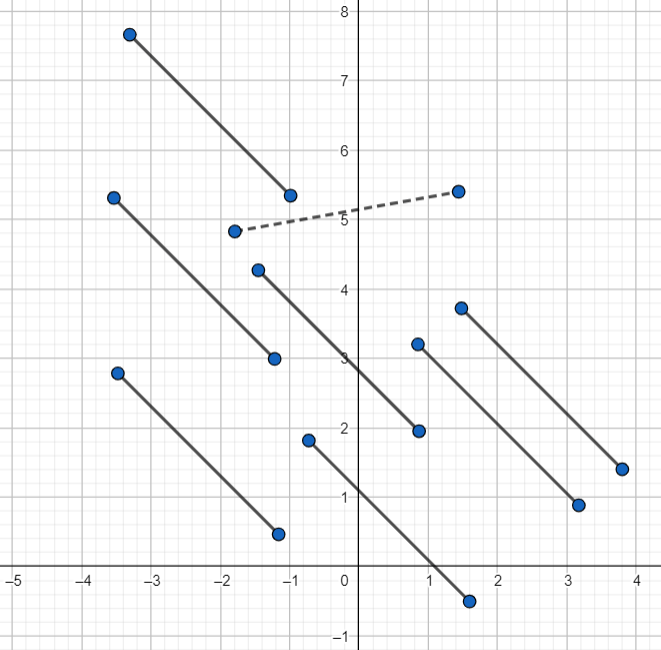
Por ejemplo, pensemos en que estamos hablando de los segmentos cerrados y acotados en el plano cartesiano. Es decir, de acuerdo a lo que estudiamos en la primera unidad, para cualesquiera dos puntos distintos $P$ y $Q$ en el plano estamos considerando el conjunto $$\overline{PQ}=\{pP+qQ:0\leq p \leq 1, 0 \leq q \leq 1, p+q=1\}.$$ En la siguiente figura puedes ver algunos de los (muchos) segmentos que hay en el plano:

¿Cómo podemos clasificar a todos los segmentos que hay en el plano? Antes de cualquier cosa, tenemos que ponernos de acuerdo en la clasificación. Una manera de hacer esto es mediante transformaciones del plano. Veamos un par de ejemplos.

Ejemplo. Una primer opción es que digamos que dos segmentos son del mismo tipo cuando podamos trasladar uno de ellos al otro. Si hacemos esto, casi todos los segmentos de la siguiente figura serían del mismo tipo.

El único que no es del mismo tipo que los demás sería el segmento punteado que, aunque lo dibujamos intencionalmente de la misma longitud que los demás, no resulta ser equivalente pues es imposible trasladarlo a alguno de los otros segmentos. Con esta noción de segmentos equivalentes, ¿qué posibilidades tendríamos? Es más o menos fácil convencerse de que para que dos segmentos sean del mismo tipo con esta clasificación necesitamos que a) sean paralelos y b) tengan la misma longitud. Por ello mismo, no es tampoco difícil convencerse del siguiente teorema de clasificación.

Teorema. Cualquier segmento del plano es equivalente bajo traslaciones a un segmento tal que uno de sus extremos es el origen.

$\square$

Veamos otra manera de clasificar los segmentos del plano.

Ejemplo. Diremos que dos segmentos son del mismo tipo si podemos llevar uno al otro a través de una isometría. Si hacemos esto entonces ahora sí todos los segmentos de la siguiente figura son equivalentes (pensando en que el segmento punteado tiene la misma longitud que los otros).

De hecho, por lo que sabemos de las isometrías podemos afirmar que bajo este criterio dos segmentos son del mismo tipo si y sólo si tienen la misma longitud. Esto nos llevaría a un teorema de clasificación un poco distinto.

Teorema. Cualquier segmento se puede mediante isometrías a un segmento que sale del origen y termina en un punto del la forma $(x,0)$ con $x>0$. Más aún, todos estos segmentos son de distinto tipo.

$\square$

En los dos ejemplos anteriores hemos sido un poco informales, pues dejamos varias cosas sin demostrar. Seguramente podrás detectarlas e intentar completar los argumentos que faltan. Algunas de estas cosas faltantes están en los ejercicios.

Más adelante…

En esta entrada hablamos de la noción de «clasificar» de manera muy general, con el fin de entenderla y ver algunas de las sutilezas que nos encontraremos más adelante. A partir de ahora nos enfocaremos en probar resultados de clasificación muy específicos, relacionados con las cónicas.

Sin embargo, queremos ser muy precisos con respecto a la clasificación que daremos. Por esta razón, en las siguientes dos entradas hablaremos de los objetos específicos que queremos clasificar y de las nociones de equivalencia que permitiremos.

Tarea moral

1. Verifica que en nuestro ejemplo de juguete la relación «tener el mismo color» es una relación de equivalencia.
2. Para cada una de las clasificaciones que dimos en nuestro ejemplo de juguete encuentra cuántas de las figuras originales hay en cada una de las clases.
3. Demuestra que la relación en $\mathbb{Z}$ en la cual tenemos a $(x,y)$ si y sólo si $x-y$ es un número par es una relación de equivalencia. Muestra que en este caso la partición consiste en el conjunto de los números pares, y el conjunto de los números impares.
4. Sea $S$ el conjunto de segmentos en el plano. Diremos un elemento $s_1$ de $S$ es traslacionalmente equivalente a otro elemento $s_2$ de $S$ si existe una traslación $T$ de $\mathbb{R}^2$ tal que $T(s_1)=s_2$. Demuestra que «ser traslacionalmente equivalente a» es una relación de equivalencia en $S$.
5. Da teoremas de clasificación de las rectas en $\mathbb{R}$ usando transformaciones para cada una de las siguientes posibilidades:
   1. Dos rectas son del mismo tipo si se puede llevar una a otra mediante una traslación.
   2. Dos rectas son del mismo tipo si se puede llevar una a la otra mediante una rotación.
   3. Dos rectas son del mismo tipo si se puede llevar una a la otra mediante una isometría.

Entradas relacionadas

• Ir a Geometría Analítica I
• Entrada anterior del curso: Homotecias y semejanzas
• Siguiente entrada del curso: Polinomios cuadráticos y curvas cuadráticas