Introducción
A lo largo de nuestros cursos hemos trabajado con el concepto de función. Intuitivamente entendemos a una función como una regla que asocia elementos entre dos conjuntos, con la condición de que a cada elemento del primer conjunto se le asigne uno y solo uno del segundo conjunto.
Para el caso complejo el concepto de función que conocemos no es una excepción, sin embargo resulta necesario introducir un nuevo concepto referente a funciones que «asignan más de un valor» a un mismo número complejo, las funciones multivaluadas. En el sentido estricto de la palabra es claro que esta idea de función carece de sentido pues rompe con la definición de lo que entendemos por función, pero para las funciones complejas esta idea resulta algo necesario al abordar el concepto de función inversa. Nuestro objetivo en esta entrada será definir esta nueva idea de «función», la cual nos permitirá ver que los conceptos de función inversa y función multivaluada están estrechamente ligados.
Observación 13.1.
Recordemos que para un número complejo $z\neq 0$, tal que $z=r\operatorname{cis}(\theta)$, con $r=|\,z\,|$ y $\theta = \operatorname{arg} z$, sus $n$-raíces complejas están dadas por: \begin{equation*} w_k = \sqrt[n]{r} \left[\operatorname{cos}\left(\frac{\theta + 2k\pi}{n}\right) + i \operatorname{sen}\left( \frac{\theta + 2k\pi}{n} \right)\right], \end{equation*} donde $k=0, 1,\ldots, n-1$.
Para motivar una definición de función multivaluada consideremos el siguiente:
Ejemplo 13.1.
De acuerdo con la observación 4.8 (entrada 4 de la primera unidad) sabemos que para $n\in\mathbb{N}^+$ la expresión $z^{1/n}$ es $n$-valuada. Si consideramos a la función $w= g(z) = z^{1/3}$, con $z\neq 0$, entonces está función es $3$-valuada, es decir, para cada valor de $z$ existen tres valores distintos de $w$ que satisfacen la ecuación $z=w^3$. Por ejemplo, para la ecuación $w^3 = 1$, si consideramos el argumento principal de $z=1$, es decir $\operatorname{Arg} z = 0$, tenemos que: \begin{align*} w_0 = 1,\\ w_1 = \frac{-1 + i\sqrt{3}}{2},\\ w_2 = \frac{-1 – i\sqrt{3}}{2}, \end{align*} son las 3 raíces cúbicas de la unidad, es decir las soluciones de la ecuación. Entonces, para $z=1$ la función $g(z) = z^{1/3}$, asigna los valores $w_0, w_1$ y $w_2$ dados.
Notemos que si consideramos a las funciones $f(z)=z^3$ y $g(z) = z^{1/3}$, entonces $g$ no puede ser la inversa de $f$ desde que $f$ no es inyectiva pues claramente $f(w_0) = 1 = f(w_1)$, pero $w_0 \neq w_1$.
Debe ser claro que en general las funciones de la forma $f(z)=z^{1/n}$, con $n\in\mathbb{N}^+$, asignan más de un valor para cada número complejo $z\neq 0$, por lo que en el sentido estricto dichas reglas de asignación no representan a una función, sino a un conjunto de funciones. Podemos visualizar este hecho en el siguiente Applet de GeoGebra https://www.geogebra.org/m/mqwkd66u.
Definición 13.1. (Función univaluada y función multivaluada.)
Sea $U\subset\mathbb{C}$ un conjunto abierto y $f:U \to \mathbb{C}$ una función. Diremos que $f$ es una función univaluada o simplemente una función compleja si para cada $z\in U$ existe un único $w\in \mathbb{C}$ tal que $f(z) = w$. En caso contrario diremos que $f$ es una función multivaluada.
Observación 13.2.
Para representar a una función multivaluada usaremos como notación letras mayúsculas, mientras que para referirnos a funciones univaluadas utilizaremos letras minúsculas, así por ejemplo, para $n\in\mathbb{N}^+$, la función $F(z) = z^{1/n}$ es multivaluada, mientras que la función $f(z) = 3z+1$ es univaluada.
Definición 13.2. (Rama de una función multivaluada.)
Sea $F(z)$ una función multivaluada definida en un dominio $D\subset\mathbb{C}$. Diremos que $f(z)$ es una rama de $F(z)$ en $D$ si:
- $f$ está bien definida en $D$, es decir $f$ es una función univaluada.
- $f(z)$ es uno de los posibles valores de $F(z)$ para cada $z\in D$.
- $f$ es continua en $D$.
Observación 13.3.
Cuando representemos ramas de una función multivaluada $F$ utilizaremos subíndices en la notación de función univaluada, por ejemplo $f_0, f_1, f_2, \ldots$.
Observación 13.4.
El concepto de dominio en la definición anterior corresponde con el de una región en el plano complejo $\mathbb{C}$, es decir, un conjunto abierto y conexo.
Observación 13.5.
Aunque en esta entrada no abordaremos formalmente el concepto de continuidad de una función compleja, utilizamos esta propiedad fuertemente en la definición de una rama de una función multivaluada, ya que en ocasiones el dominio de una función multivaluada no corresponderá con el dominio de una rama puesto que puede suceder que la función univaluada no sea continua en dicho conjunto, como veremos en los ejemplos 13.2 y 13.4. Para mayor detalle sobre el concepto de continuidad se puede consultar la entrada 15 de esta unidad.
Ejemplo 13.2.
En la definición 4.1, de la entrada 4, se específico que la notación usada para referirnos al argumento de un número complejo, es decir $\operatorname{arg} z$, no representa a una función de $z$, ya que dicha notación describe a un conjunto de números reales $\theta$ que satisfacen las ecuaciones: \begin{equation*} \text{sen}(\theta) = \frac{\text{Re}(z)}{|\, z \,|}, \quad \text{cos}(\theta) = \frac{\text{Im}(z)}{|\, z \,|}. \tag{13.1} \end{equation*}
Considerando el concepto de función multivaluada podemos hablar de la función $F(z) = \operatorname{arg}(z)$, la cual asignará a cada número complejo $z\neq 0$ una infinidad de argumentos que satisfacen las ecuaciones (13.1), ya que para cada $n\in\mathbb{Z}$, si $\theta\in\mathbb{R}$ satisface las ecuaciones (13.1), entonces $\theta + 2\pi n$ también lo hará.
Si fijamos un valor de $k\in\mathbb{Z}$, obtenemos una función univaluda que comunmente es llamada «rama» de la función $F(z)= \operatorname{arg}(z)$. Es importante hacer énfasis aquí en el hecho de que esta «rama» no es necesariamente una rama en el sentido estricto de la palabra, es decir de acuerdo con la definición 13.2, pues como veremos en el ejemplo 15.6 de la entrada 15, la función argumento es continua en el dominio $\mathbb{C}\setminus\left(-\infty,0\right]$, mientras que la función multivaluada $F(z)= \operatorname{arg}(z)$ está definida en el dominio $\mathbb{C}\setminus\{0\}$.
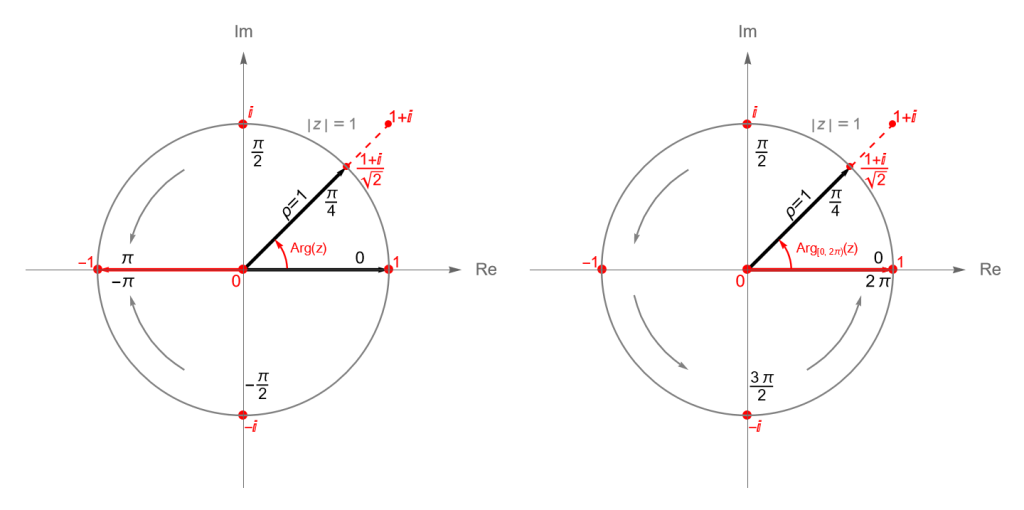
Es claro que existen infinitas ramas, en particular, si elegimos el valor $k = 0$, obtenemos la rama que denominamos la rama principal, que corresponde con el argumento principal de un número complejo $z\neq 0$, es decir $\operatorname{Arg} z \in (-\pi, \pi]$.
Definición 13.3. (Argumento principal.)
Sea $U = \mathbb{C}\setminus{0}$. Definimos a la función compleja {\bf argumento principal} como la función $f: U \to (-\pi, \pi]$, denotada como $f(z) = \operatorname{Arg}(z)$, dada por: \begin{equation*} \operatorname{Arg}(z) = \left\{ \begin{array}{lcc} \text{arctan}\left(\frac{y}{x}\right) & \text{si} & x>0,\\ \text{arctan}\left(\frac{y}{x}\right) + \pi & \text{si} & x<0 \quad \text{y} \quad y\geq 0,\\ \text{arctan}\left(\frac{y}{x}\right) – \pi & \text{si} & x<0 \quad \text{y} \quad y<0,\\ \frac{\pi}{2} & \text{si} & x=0 \quad \text{y} \quad y>0,\\ -\frac{\pi}{2} & \text{si} & x=0 \quad \text{y} \quad y<0,\\ \text{No definido} & \text{si} & x=0 \quad \text{y} \quad y=0. \end{array} \right. \end{equation*}
Notemos que tanto la función multivaluada $F(z) = \operatorname{arg}(z)$ como la función univaluada $f(z) = \operatorname{Arg}(z)$ están definidas en $\mathbb{C}\setminus\{0\}$ y toman valores en intervalos reales de la forma $\left((2n-1)\pi, (2n+1)\pi\right]$, con $n\in\mathbb{Z}$, por lo que su gráfica tiene lugar en $\mathbb{R}^3$. Podemos visualizar estas gráficas en el siguiente Applet de GeoGebra: https://www.geogebra.org/m/cwt5ctuf.
Procedemos a deducir una nueva expresión para obtener el argumento principal de un número complejo que nos será de utilidad más adelante.
Proposición 13.1.
Sea $z = x+iy \in \mathbb{C}\setminus\{0\}$, entonces: \begin{equation*} \operatorname{Arg}(z) = \left\{ \begin{array}{lcc} 2 \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right) & \text{si} & z\not\in \mathbb{R}^{-},\\ \pi & \text{si} & z\in \mathbb{R}^{-},\ \end{array} \right. \end{equation*} donde $\mathbb{R}^{-} = (-\infty, 0)$.
Demostración. Sea $z = x+iy \in \mathbb{C}\setminus{0}$.
Supongamos que $z\in \mathbb{R}^{-}$, entonces: \begin{equation*} z = -|\,z\,| = |\,z\,| \left[\operatorname{cos}(\pi) + i \operatorname{sen}(\pi)\right] = |\,z\,| \operatorname{cis}(\pi), \end{equation*} por lo que $\operatorname{Arg}(z) = \pi \in \operatorname{arg} z$ y claramente $\pi \in (-\pi,\pi]$.
Supongamos ahora que $z\not\in \mathbb{R}^{-}$, consideremos a: \begin{equation*} \theta_0:= 2 \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right). \end{equation*}
Como $z\neq 0$, entonces tenemos que: \begin{align*} \theta_0 & = 2 \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right)\\ & = 2 \operatorname{arc tan}\left(\dfrac{\dfrac{y}{|\,z\,|}}{\dfrac{|\,z\,| + x}{|\,z\,|}}\right)\\ & = 2 \operatorname{arc tan}\left(\dfrac{\dfrac{y}{|\,z\,|}}{1 + \dfrac{x}{|\,z\,|}}\right)\\ & := 2 \operatorname{arc tan}\left(\dfrac{b}{1 + a}\right), \end{align*}
de donde: \begin{equation*} \tan\left(\frac{\theta_0}{2}\right) = \dfrac{b}{1 + a}. \end{equation*}
Recordemos que se cumplen las siguientes identidades trigonométricas: \begin{equation*} \tan\left(\frac{\theta_0}{2}\right) = \dfrac{\operatorname{sen}(\theta_0)}{1 + \operatorname{cos}(\theta_0)}, \quad \tan^2\left(\frac{\theta_0}{2}\right) = \dfrac{1 – \operatorname{cos}(\theta_0)}{1 + \operatorname{cos}(\theta_0)}, \quad \tan\left(\frac{\theta_0}{2}\right) = \dfrac{2 \operatorname{tan}\left(\frac{\theta_0}{2}\right)}{1 – \tan^2\left(\frac{\theta_0}{2}\right)}, \end{equation*} por lo que: \begin{equation*} \operatorname{sen}(\theta_0) = \dfrac{2 \operatorname{tan}\left(\frac{\theta_0}{2}\right)}{1 + \tan^2\left(\frac{\theta_0}{2}\right)} = b, \end{equation*} \begin{equation*} \operatorname{cos}(\theta_0) = \dfrac{1 – \tan^2\left(\frac{\theta_0}{2}\right)}{1 + \tan^2\left(\frac{\theta_0}{2}\right)} = a. \end{equation*}
Más aún, dado que $z\neq 0$ y $z\not\in \mathbb{R}^{-}$, es decir $z\not\in (-\infty, 0] = \left\{z = x+iy : x\leq 0, y =0\right\}$, para $z=x+iy$ se cumple que $x>0$ ó $y\neq 0$, por lo que $|\,z\,| + x >0$, entonces: \begin{equation*} \operatorname{arc tan}\left(\dfrac{y}{|\,z\,| + x}\right) \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right), \end{equation*} de donde $\theta_0 \in (-\pi, \pi)$ y: \begin{equation*} z = |\,z\,| \left[\operatorname{cos}(\theta_0) + i \operatorname{sen}(\theta_0)\right] = |\,z\,| \operatorname{cis}(\theta_0). \end{equation*} Por lo tanto, $\theta_0 = \operatorname{Arg}(z)$.
$\blacksquare$
Observación 13.6.
De acuerdo con los resultados de la entrada 4, Unidad I, sabemos que para $z_1,z_2\in\mathbb{C}\setminus\{0\}$, se cumple que: \begin{equation*} \operatorname{arg} z_1 z_2 = \operatorname{arg} z_1 + \operatorname{arg} z_2 = \operatorname{Arg} z_1 + \operatorname{Arg} z_2 + 2\pi n, \quad n\in\mathbb{Z}, \end{equation*} \begin{equation*} \operatorname{arg} \frac{z_1}{z_2} = \operatorname{arg} z_1 – \operatorname{arg} z_2 = \operatorname{Arg} z_1 – \operatorname{Arg} z_2 + 2\pi n, \quad n\in\mathbb{Z}, \end{equation*} \begin{equation*} \operatorname{arg} z_1^k = k \operatorname{arg} z_1 = k \operatorname{Arg} z_1 + 2\pi n, \quad k, n\in\mathbb{Z}, \end{equation*} donde $\operatorname{Arg} z \in (-\pi, \pi]$.
Es importante recordar que estas igualdades son entre conjuntos. Sin embargo, considerando la definición de función multivaluada es claro que estas propiedades se heredan a la función multivaluada $G(z) = \operatorname{arg}(z)$, para $z\neq 0$.
Más aún, de nuestros cursos de Cálculo sabemos que la función $f(x) = [x]$, llamada parte entera, determina el mayor entero menor o igual a $x$. Para $x\in\mathbb{R}$ y $n\in\mathbb{Z}$ dicha función cumple que: \begin{equation*} [x] = n \quad \Longleftrightarrow \quad x-1 < n \leq x \quad \Longleftrightarrow \quad n \leq x < n+1. \end{equation*}
Notemos que mediante esta función podemos obtener una expresión para determinar el argumento principal de un número complejo a través de cualquier elemento del conjunto de argumentos, es decir, para $z\in\mathbb{C}$, con $z\neq 0$, sabemos que: \begin{equation*} \operatorname{arg} z = \operatorname{Arg} z + 2\pi k, \quad k\in\mathbb{Z}, \end{equation*} de donde: \begin{equation*} \operatorname{Arg} z = \operatorname{arg} z + 2\pi n, \quad n=-k\in\mathbb{Z}. \end{equation*}
Puesto que $\operatorname{Arg} z \in (-\pi, \pi]$, entonces: \begin{equation*} -\pi < \operatorname{arg} z + 2\pi n \leq \pi \quad \Longleftrightarrow \quad \frac{1}{2} – \frac{\operatorname{arg} z}{2\pi} – 1 < n \leq \frac{1}{2} – \frac{\operatorname{arg} z}{2\pi}, \end{equation*} es decir: \begin{equation*} \operatorname{Arg} z = \operatorname{arg} z + 2\pi \left[ \frac{1}{2} – \frac{\operatorname{arg} z}{2\pi}\right], \end{equation*} donde $[\,x\,]$ corresponde con la función parte entera y $\operatorname{arg} z$ es un argumento $\theta$ cualquiera que satisface (13.1).
De acuerdo con observación anterior, no es difícil verificar que la función argumento principal definida antes, satisface las siguientes propiedades.
Proposición 13.2. (Propiedades argumento principal.)
Sean $z_1, z_2 \in \mathbb{C}\setminus\{0\}$, entonces:
- $\operatorname{Arg}(z_1 z_2) = \operatorname{Arg}(z_1) + \operatorname{Arg}(z_2) + 2\pi N_{+}$,
- $\operatorname{Arg}\left(\dfrac{z_1}{z_2}\right) = \operatorname{Arg}(z_1) – \operatorname{Arg}(z_2) + 2\pi N_{-}$, donde $N_{\pm}$ son números enteros dados por: \begin{equation*} N_{\pm} = \left\{ \begin{array}{lcc} -1 & \text{si} & \operatorname{Arg}(z_1) \pm \operatorname{Arg}(z_2) > \pi, \\ 0 & \text{si} & -\pi < \operatorname{Arg}(z_1) \pm \operatorname{Arg}(z_2) \leq \pi, \\ 1 & \text{si} & \operatorname{Arg}(z_1) \pm \operatorname{Arg}(z_2) \leq -\pi. \end{array} \right. \end{equation*}
- \begin{equation*}
\operatorname{Arg}\left(z_1^{-1}\right) = \operatorname{Arg}\left(\overline{z_1}\right) = \left\{ \begin{array}{lcc} \operatorname{Arg}\left(z_1\right) & \text{si} & \operatorname{Im}(z_1) =0 \, \, \, \, \text{y} \,\,\,\, z_1\neq 0,\\ -\operatorname{Arg}\left(z_1\right) & \text{si} & \operatorname{Im}(z_1) \neq 0. \end{array} \right. \end{equation*} - Para todo $n\in\mathbb{Z}$ se cumple que: \begin{equation*} \operatorname{Arg}\left(z_1^n\right) = n\, \operatorname{Arg}\left(z_1\right) + 2\pi N_{n}, \end{equation*} donde $N_n$ es un número entero dado por: \begin{equation*} N_n = \left[ \frac{1}{2} – \frac{n}{2\pi}\operatorname{Arg}(z_1)\right], \end{equation*} con $[\, x \,]$ la función parte entera de $x$.
Demostración. Sean $z_1, z_2 \in \mathbb{C}\setminus\{0\}$.
- Sean $\theta_1 = \operatorname{Arg}(z_1)$ y $\theta_1 = \operatorname{Arg}(z_2)$, entonces $\theta_1, \theta_2 \in (-\pi, \pi]$, por lo que: \begin{equation*} -2\pi < \theta_1 + \theta_2 \leq 2\pi \quad \Longleftrightarrow \quad -2\pi \leq -\left(\theta_1 + \theta_2\right) < 2\pi. \end{equation*} De acuerdo con la observación 13.6 es claro que: \begin{equation*} \operatorname{Arg}(z_1 z_2) = \theta_1 + \theta_2 + 2\pi N_{+}, \end{equation*} donde $N_{+} = \left[ \dfrac{1}{2} – \dfrac{\theta_1 + \theta_2}{2\pi}\right] \in \mathbb{Z}$.
Entonces: \begin{equation*} -\dfrac{1}{2} – \frac{2\pi}{2\pi} \leq -\dfrac{1}{2} – \dfrac{\theta_1 + \theta_2}{2\pi} < N_{+} \leq \dfrac{1}{2} – \dfrac{\theta_1 + \theta_2}{2\pi} < \dfrac{1}{2} + \dfrac{2\pi}{2\pi}, \end{equation*} es decir $-\dfrac{3}{2} < N_{+} < \dfrac{3}{2}$, por lo que $N_{+} \in \left\{-1, 0, 1\right\}$.
Dado que $ \operatorname{Arg}(z_1 z_2) \in (-\pi, \pi]$, entonces: \begin{equation*} -\pi < \theta_1 + \theta_2 +2\pi N_{+} \leq \pi. \end{equation*} Si $ -2\pi < \theta_1 + \theta_2 \leq -\pi$, entonces $N_{+} = 1$. Mientras que si $ \pi < \theta_1 + \theta_2 \leq 2\pi$, entonces $N_{+} = -1$. - Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se sigue de la observación 13.6.
$\blacksquare$
Ejemplo 13.3.
Sean $z_1 = i$ y $z_2 = -1$. Calcular:
a) $\operatorname{Arg}(z_1 z_2)$.
Solución. Tenemos que $z_1 z_2 = -i$, por lo que $\operatorname{Arg}\left(z_1 z_2\right) = -\dfrac{\pi}{2}$.
Por otra parte, tenemos que $\operatorname{Arg}\left(z_1\right) = \dfrac{\pi}{2}$ y $\operatorname{Arg}\left(z_2\right) = \pi$, por lo que: \begin{equation*} \operatorname{Arg}\left(z_1\right) + \operatorname{Arg}\left(z_2\right) = \dfrac{\pi}{2} + \pi = \frac{3\pi}{2}. \end{equation*} De acuerdo con la propiedad 1, como $\operatorname{Arg}\left(z_1\right) + \operatorname{Arg}\left(z_2\right) > \pi$, entonces: \begin{equation*} \operatorname{Arg}(z_1 z_2) = -\frac{\pi}{2} = \operatorname{Arg}(z_1) + \operatorname{Arg}(z_2) -2\pi. \end{equation*} b) $\operatorname{Arg}\left(z_2^{-1}\right)$.
Solución. Como $\operatorname{Im}(z_2) = 0$ y $z_2\neq 0$, entonces por la propiedad 3 tenemos que: \begin{equation*} \operatorname{Arg}\left(z_2^{-1}\right) = \operatorname{Arg}(z_2) = \pi. \end{equation*} c) $\operatorname{Arg}(z_1^2)$.
Solución. Dado que $\operatorname{Arg}\left(z_1\right) = \dfrac{\pi}{2}$, entonces considerando la propiedad 4 tenemos que: \begin{align*} \operatorname{Arg}\left(z_1^2\right) & = 2 \left(\dfrac{\pi}{2}\right) + 2\pi \left[ \frac{1}{2} – \frac{2}{2\pi} \left(\dfrac{\pi}{2}\right)\right]\\ & = \pi + 2\pi(0)\\ & = \pi. \end{align*}
Observación 13.7.
De nuestros cursos de Cálculo sabemos que las funciones reales seno y coseno son continuas en $\mathbb{R}$ y que para todo $x\in\mathbb{R}$ se cumple que: \begin{equation*} -1 \leq \operatorname{sen}(x) \leq 1 \quad \text{y} \quad -1 \leq \operatorname{cos}(x) \leq 1. \end{equation*}
Por lo que, si $r,s \in [-1,1]$, entonces existen $x,y\in\mathbb{R}$ tales que: \begin{equation*} \operatorname{sen}(y) = s \quad \text{y} \quad \operatorname{cos}(x) = r. \end{equation*}
Si imponemos la condición $r^2 + s^2 = 1$, es decir que $(r,s)$ cae en la circunferencia unitaria de $\mathbb{R}^2$, entonces se cumple que: \begin{equation*} \operatorname{sen}(y) = \pm \operatorname{sen}(x) = \operatorname{sen}\left(\pm x\right). \end{equation*}
Dado que $\operatorname{cos}\left( \pm x\right) = \operatorname{cos}(x)$, entonces existe $\theta\in\mathbb{R}$ tal que: \begin{equation*} s = \operatorname{sen}\left(\theta\right) \quad \text{y} \quad r = \operatorname{cos}\left(\theta\right). \end{equation*}
Observación 13.8.
Sea $x\in\mathbb{R}$. Definimos: \begin{equation*} x^*:= x – 2\left[\frac{x}{2\pi}\right] \pi. \end{equation*}
De acuerdo con la observación 13.6 sabemos que $\left[\frac{x}{2\pi}\right] \leq \frac{x}{2\pi} < \left[\frac{x}{2\pi}\right] + 1$, entonces $ 0\leq x^* < 2\pi$ y: \begin{equation*} \operatorname{sen}(x^*) = \operatorname{sen}(x), \quad \operatorname{cos}(x^*) = \operatorname{cos}(x). \end{equation*}
En general, para $\alpha, x\in\mathbb{R}$ definimos: \begin{equation*} x^{**} := \left\{ \begin{array}{lcc} x^* + 2\left( \left[\frac{\alpha}{2\pi}\right] + 1\right) \pi & \text{si} & x^* + 2\left[\frac{\alpha}{2\pi}\right]\pi < \alpha, \\ x^* + 2 \left[\frac{\alpha}{2\pi}\right] \pi & \text{si} & x^* + 2\left[\frac{\alpha}{2\pi}\right]\pi \geq \alpha. \end{array} \right. \end{equation*}
Entonces $ \alpha \leq x^{**} < \alpha + 2\pi$ y: \begin{equation*} \operatorname{sen}(x^{**}) = \operatorname{sen}(x), \quad \operatorname{cos}(x^{**}) = \operatorname{cos}(x). \end{equation*}
De las observaciones 13.7 y 13.8 tenemos que si $r,s\in\mathbb{R}$, con $r^2+s^2 = 1$, entonces dado $\alpha\in\mathbb{R}$ existe $\theta \in [\alpha, \alpha+2\pi)$ tal que:
\begin{equation*} s = \operatorname{sen}\left(\theta\right) \quad \text{y} \quad r = \operatorname{cos}\left(\theta\right). \end{equation*}
Notemos que dicho $\theta$ es único. Supongamos que existen $\theta, \theta’ \in [\alpha, \alpha+2\pi)$ tales que: \begin{equation*} \operatorname{sen}\left(\theta\right) = s = \operatorname{sen}\left(\theta’\right) \quad \text{y} \quad \operatorname{cos}\left(\theta\right) = r = \operatorname{cos}\left(\theta’\right), \end{equation*} entonces $\operatorname{cos}(\theta-\theta’) = \operatorname{sen}^2\left(\theta\right) + \operatorname{cos}^2\left(\theta\right) = 1$, pero lo anterior solo es posible si y solo si $\theta – \theta’ = 2k\pi$ para algún $k\in\mathbb{Z}$.
Puesto que $\theta, \theta’ \in [\alpha, \alpha+2\pi)$ y $\theta = \theta’ + 2k\pi$, para algún $k\in\mathbb{Z}$, entonces $k = 0$ y por tanto $\theta = \theta’$.
Más aún, dado que para todo $\alpha\in\mathbb{R}$ se cumple que: \begin{equation*} \operatorname{sen}(\alpha + 2\pi) = \operatorname{sen}(\alpha) \quad \text{y} \quad \operatorname{cos}(\alpha + 2\pi) = \operatorname{cos}(\alpha), \end{equation*} entonces existe un único $\theta’ \in (\alpha, \alpha + 2\pi]$ tal que: \begin{equation*} s = \operatorname{sen}\left(\theta’\right) \quad \text{y} \quad r = \operatorname{cos}\left(\theta’\right). \end{equation*}
Considerando lo anterior, podemos definir una rama arbitraria de la función multivaluada $F(z) = \operatorname{arg}(z)$.
Definición 13.4. (Rama del argumento en un intervalo $I$.)
Sean $\alpha\in\mathbb{R}$, $z\in\mathbb{C}\setminus\{0\}$ y sea $I\subset\mathbb{R}$ un intervalo semiabierto de longitud $2\pi$, es decir de la forma $[\alpha, \alpha + 2\pi)$ ó $(\alpha, \alpha + 2\pi]$. Al único número real $\theta\in I$ tal que: \begin{equation*} \text{sen}(\theta) = \frac{\text{Re}(z)}{|\, z \,|} \quad \text{y} \quad \text{cos}(\theta) = \frac{\text{Im}(z)}{|\, z \,|}, \end{equation*} lo llamaremos el argumento de $z$ en $I$ y lo denotaremos como $\operatorname{Arg}_{I} z$.
La utilidad de la definición 13.4 la veremos cuando definamos al logaritmo complejo, pues en ocasiones el trabajar con ramas distintas de la principal nos permitirá hablar de ciertas funciones en las que tengamos que estudiar algunas de sus propiedades como la continuidad y la analicidad.
Considerando la definición 13.4, es posible definir a la función $\operatorname{Arg}_{I}: \mathbb{C}\setminus\{0\} \to I$ como $\operatorname{Arg}_{I}(z) = $ el único valor de $\operatorname{arg} z$ que pertenece a $I$.
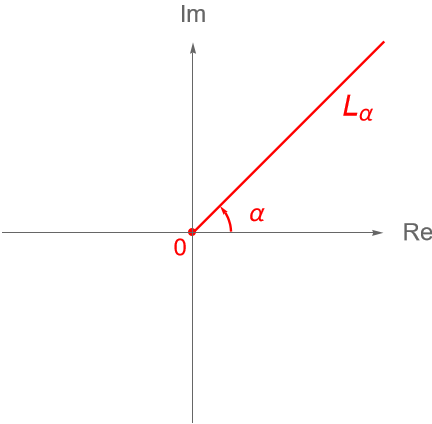
Observación 13.9.
En general la función $\operatorname{Arg}_{I}(z)$ será una rama, de acuerdo con la definición 13.2, siempre que se defina sobre el dominio $\mathbb{C}\setminus L\alpha$, con $L_\alpha = \{r\operatorname{cis}(\alpha) : r\geq 0\}$, figura 60, es decir todo el plano complejo menos la semirrecta que parte desde el origen y que forma un ángulo $\alpha$ con respecto al eje real positivo, pues en dicha semirrecta la función no es continua, como veremos en el ejemplo 15.6 de la entrada 15.
Observación 13.10.
Notemos que si $\alpha=-\pi$ e $I = (\alpha, \alpha + 2\pi]$, entonces para $z\neq 0$ se cumple que $\operatorname{Arg}(z) = \operatorname{Arg}_{(-\pi, \pi]}(z)$, es decir obtenemos la rama principal o el argumento principal. Mientras que si consideramos a $\alpha=0$ e $I = [\alpha, \alpha + 2\pi)$, entonces para $z\neq 0$ obtenemos $\operatorname{Arg}_{[0, 2\pi)}(z)$ que suele llamarse el argumento natural de $z$.
Podemos deducir que el argumento principal y el argumento natural de un número complejo $z\neq 0$ están relacionados como sigue: \begin{equation*} \operatorname{Arg}(z) = \left\{ \begin{array}{lcc} \operatorname{Arg}_{[0, 2\pi)}(z) & \text{si} & 0 \leq \operatorname{Arg}_{[0, 2\pi)}(z) \leq \pi, \\ \operatorname{Arg}_{[0, 2\pi)}(z) – 2\pi & \text{si} & \pi < \operatorname{Arg}_{[0, 2\pi)}(z) < 2 \pi. \end{array} \right. \end{equation*} \begin{equation*} \operatorname{Arg}_{[0, 2\pi)}(z) = \left\{ \begin{array}{lcc} \operatorname{Arg}(z) & \text{si} & 0 \leq \operatorname{Arg}(z) \leq \pi, \\ \operatorname{Arg}(z) + 2\pi & \text{si} & -\pi < \operatorname{Arg}(z) < 0. \end{array} \right. \end{equation*}
Gráficamente podemos ver dónde toman valores el argumento principal y el argumento natural de un número complejo $z\neq 0$, figura 61.
Ejemplo 13.4.
Si consideramos $\alpha=-\pi$ e $I = (\alpha, \alpha + 2\pi]$, entonces para $z=-1-i$ tenemos que: \begin{equation*} \operatorname{Arg}_{(-\pi, \pi]}(z) = -\frac{3\pi}{4}. \end{equation*}
Por otra parte si consideramos $\alpha=0$ e $I = [\alpha, \alpha + 2\pi)$, entonces para $z=-1-i$ tenemos que: \begin{equation*} \quad \operatorname{Arg}_{[0, 2\pi)}(z) = \frac{5\pi}{4}. \end{equation*}
Procedemos a establecer un resultado que relacione a la función $\operatorname{Arg}_{I}(z)$ con las funciones $\operatorname{Arg}(z)$ y $\operatorname{Arg}{[0, 2\pi)}(z)$.
Proposición 13.3.
Sean $z\neq 0$, $\alpha\in\mathbb{R}$ y sea $I\subset\mathbb{R}$ un intervalo semiabierto de longitud $2\pi$, es decir de la forma $[\alpha, \alpha + 2\pi)$ ó $(\alpha, \alpha + 2\pi]$.
- Si $I= [\alpha, \alpha + 2\pi)$, entonces: $\operatorname{Arg}_{I}(z) = \operatorname{Arg}_{[0,2\pi)}\left(z \operatorname{cis}(-\alpha)\right) + \alpha$.
- Si $I= (\alpha, \alpha + 2\pi]$, entonces: $\operatorname{Arg}_{I}(z) = \operatorname{Arg}\left(-z \operatorname{cis}(-\alpha)\right) + \alpha + \pi$.
Demostración. Dadas las hipótesis, primero notemos que para cualesquiera $\theta,\alpha\in\mathbb{R}$ se cumple que: \begin{align*} \operatorname{cis}(\theta-\alpha) & = \operatorname{cos}(\theta – \alpha) + i \operatorname{sen}(\theta – \alpha)\\ & = \operatorname{cos}(\theta) \operatorname{cos}(\alpha) + \operatorname{sen}(\theta) \operatorname{sen}(\alpha)\\ & \quad \quad + i \left[ \operatorname{sen}(\theta) \operatorname{cos}(\alpha) – \operatorname{sen}(\alpha) \operatorname{cos}(\theta) \right]\\ & = \operatorname{cos}(\alpha) \left[ \operatorname{cos}(\theta) + i \operatorname{sen}(\theta) \right] – i \operatorname{sen}(\alpha) \left[ \operatorname{cos}(\theta) + i \operatorname{sen}(\theta) \right]\\ & = \operatorname{cis}(\theta) \left[ \operatorname{cos}(-\alpha) + i \operatorname{sen}(-\alpha) \right] \\ & = \operatorname{cis}(\theta) \operatorname{cis}(-\alpha). \end{align*}
- Sea $I= [\alpha, \alpha + 2\pi)$. Si $\theta \in I$ y $\theta = \operatorname{Arg}_{I}(z)$ entonces $z = |\,z\,| \operatorname{cis}(\theta)$ y: \begin{equation*} \alpha \leq \theta < \alpha + 2\pi \quad \Longleftrightarrow \quad 0 \leq \theta – \alpha < 2\pi, \end{equation*} por lo que: \begin{align*} \theta – \alpha & = \operatorname{Arg}_{[0,2\pi)}\left( \operatorname{cis}(\theta -\alpha)\right)\\ & = \operatorname{Arg}_{[0,2\pi)}\left( \operatorname{cis}(\theta) \operatorname{cis}(-\alpha)\right)\\ & = \operatorname{Arg}_{[0,2\pi)}\left( \frac{z}{|\,z\,|} \operatorname{cis}(-\alpha)\right)\\ & = \operatorname{Arg}_{[0,2\pi)}\left( z \operatorname{cis}(-\alpha)\right), \end{align*} de donde: \begin{equation*} \theta = \operatorname{Arg}_{I}(z) = \operatorname{Arg}_{[0,2\pi)}\left(z \operatorname{cis} (-\alpha)\right) + \alpha. \end{equation*}
- Sea $I= (\alpha, \alpha + 2\pi]$. Si $\theta \in I$ y $\theta = \operatorname{Arg}_{I}(z)$ entonces $z = |\,z\,| \operatorname{cis}(\theta)$ y: \begin{equation*} \alpha < \theta \leq \alpha + 2\pi \quad \Longleftrightarrow \quad -\pi < \theta – \alpha -\pi \leq \pi, \end{equation*} por lo que: \begin{align*} \operatorname{cis}(\theta – \alpha – \pi) & = \operatorname{cos}(\theta – \alpha – \pi) + i \operatorname{sen}(\theta – \alpha – \pi)\\ & = \operatorname{cos}(\pi) \left [\operatorname{cos}(\theta – \alpha) + i \operatorname{sen}(\theta – \alpha) \right]\\ & = – \operatorname{cis}(\theta) \operatorname{cis}(-\alpha). \end{align*} Entonces: \begin{align*} \theta – \alpha – \pi & = \operatorname{Arg}\left( \operatorname{cis}(\theta -\alpha – \pi)\right)\\ & = \operatorname{Arg}\left( -\operatorname{cis}(\theta) \operatorname{cis}(-\alpha)\right)\\ & = \operatorname{Arg}\left( \frac{z}{|\,z\,|} \operatorname{cis}(-\alpha)\right)\\ & = \operatorname{Arg}\left(-z \operatorname{cis}(-\alpha)\right), \end{align*} de donde: \begin{equation*} \theta = \operatorname{Arg}_{I}(z) = \operatorname{Arg}\left(-z \operatorname{cis} (-\alpha) \right) + \alpha + \pi. \end{equation*}
$\blacksquare$
Ejemplo 13.5.
Sea $\alpha=3\pi/2$. Si $I = [\alpha, \alpha + 2\pi)$, entonces: \begin{equation*} I = \left[\frac{3\pi}{2}, \frac{7\pi}{2}\right). \end{equation*}
Sabemos que: \begin{equation*} \operatorname{cis} \left(-\frac{3\pi}{2}\right) = \operatorname{cos} \left(-\frac{3\pi}{2}\right) + i \operatorname{sen} \left(-\frac{3\pi}{2}\right) = 0 + i(1) = i. \end{equation*}
Notemos que si $z\in \mathbb{R}^+$, es decir $z>0$, entonces: \begin{align*} \operatorname{Arg}_{\left[\frac{3\pi}{2}, \frac{7\pi}{2}\right)}(z) & = \operatorname{Arg}_{[0,2\pi)}\left(z \operatorname{cis} \left(-\frac{3\pi}{2}\right)\right) + \frac{3\pi}{2}\\ & = \operatorname{Arg}_{[0,2\pi)}\left(z i\right) + \frac{3\pi}{2}\\ & = \frac{\pi}{2} + \frac{3\pi}{2}\\ & = 2\pi. \end{align*}
Por otra parte, para $z=i$ tenemos que: \begin{equation*} i \, \operatorname{cis} \left(-\frac{3\pi}{2}\right) = i^2 = -1, \end{equation*} por lo que: \begin{align*} \operatorname{Arg}_{\left[\frac{3\pi}{2}, \frac{7\pi}{2}\right)}(i) & = \operatorname{Arg}_{[0,2\pi)}\left(i \operatorname{cis} \left(-\frac{3\pi}{2}\right)\right) + \frac{3\pi}{2}\\ & = \operatorname{Arg}_{[0,2\pi)}\left(-1\right) + \frac{3\pi}{2}\\ & = \pi + \frac{3\pi}{2}\\ & = \frac{5\pi}{2}. \end{align*}
Ejemplo 13.6.
Sea $\alpha=3\pi/2$. Si $I = (\alpha, \alpha + 2\pi]$, entonces: \begin{equation*} I = \left(\frac{3\pi}{2}, \frac{7\pi}{2}\right]. \end{equation*}
Para $z=i$ tenemos que: \begin{equation*} -i \, \operatorname{cis} \left(-\frac{3\pi}{2}\right) = – i^2 = 1, \end{equation*}
por lo que: \begin{align*} \operatorname{Arg}_{\left(\frac{3\pi}{2}, \frac{7\pi}{2}\right]}(i) & = \operatorname{Arg}\left(- i \operatorname{cis} \left(-\frac{3\pi}{2}\right)\right) + \frac{3\pi}{2} + \pi\\ & = \operatorname{Arg}\left(1\right) + \frac{5\pi}{2}\\ & = 0 + \frac{5\pi}{2}\\ & = \frac{5\pi}{2}. \end{align*}
Observación 13.11.
En el caso real para garantizar la existencia de la inversa de la función $f(x) = x^2$, bastaba con restringir el dominio de $f$ al intervalo $[0, \infty )$. Sin embargo, dado que en $\mathbb{C}$ el orden inducido en $\mathbb{R}$, bajo la relación «$>0$», no es válido y considerando el hecho de que nuestro candidato para ser la inversa de la función $f(z) = z^2$, es decir la función $F(z) = z^{1/2}$ es una función multivaluada, entonces para el caso complejo debemos ser aún más minuciosos en la elección del dominio al que debemos restringir a la función $f(z) = z^2$ para que sea inyectiva y por tanto invertible.
Ejemplo 13.7.
En el ejemplo 12.7(a) vimos que la función compleja $f(z) = z^2$ no es inyectiva, por lo que no es biyectiva y de acuerdo con la definición 12.4 no podemos hablar de su función inversa. Veamos que si restringimos el dominio de esta función es posible garantizar que $f$ es inyectiva.
Solución. De acuerdo con la observación 13.1 tenemos que para $n=2$ y $z\neq 0$, la función $f(z) = z^2$ tiene dos raíces, las cuales están dadas por: \begin{equation*} w_k = \sqrt{r} \left[\operatorname{cos}\left(\frac{\theta + 2k\pi}{2}\right) + i \operatorname{sen}\left( \frac{\theta + 2k\pi}{2} \right)\right], \tag{13.2} \end{equation*} donde $k=0, 1$.
Definimos el siguiente dominio: \begin{equation*} D= \left\{z\in\mathbb{C} : -\frac{\pi}{2} < \operatorname{arg} z \leq \frac{\pi}{2}\right\}. \tag{13.3} \end{equation*}
Veamos que $f$ es inyectiva en $D$. Sean $z_1, z_2 \in D$, con $z_1 = r_1 \operatorname{cis}(\theta_1)$ y $z_2 = r_2 \operatorname{cis}(\theta_2)$ ambos distintos de cero, entonces $\theta_1, \theta_2 \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right]$.
Supongamos que $f(z_1) = f(z_2)$, entonces por la fórmula de De Moivre tenemos que: \begin{equation*} r_1^2 \operatorname{cis}(2\theta_1) = r_2^2 \operatorname{cis}(2\theta_2), \end{equation*} de donde es claro que los números complejos $z_1^2$ y $z_2^2$ tienen el mismo módulo y el mismo argumento principal, es decir: \begin{equation*} r_1^2=r_2^2 \quad \text{y} \quad \operatorname{Arg} z_1^2 = \operatorname{Arg} z_2^2. \end{equation*}
Dado que $r_1, r_2>0$, entonces $r_1 = r_2$. Por otra parte, como $\theta_1, \theta_2 \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right]$, entonces: \begin{equation*} -\pi < 2\theta_1 \leq \pi \quad \text{y} \quad -\pi < 2\theta_2 \leq \pi, \end{equation*} por lo que $\operatorname{Arg} z_1^2 = 2\theta_1$ y $\operatorname{Arg} z_2^2 = 2\theta_2$, es decir $2\theta_1 = 2\theta_2$, entonces $\theta_1 = \theta_2$. Por lo tanto, como $z_1$ y $z_2$ tienen el mismo módulo y el mismo argumento principal, concluimos que $z_1 = z_2$.
Así, $f$ restringida al dominio $D$, dado en (13.3), es inyectiva.
En general, para la función compleja $f(z) = z^n$, con $n\geq 2$, el planteamiento dado en este último ejemplo puede utilizarse para garantizar que dicha función es inyectiva, solo habría que modificar el dominio dado en (13.3) por: \begin{equation*} D_n = \left\{z\in\mathbb{C} : -\frac{\pi}{n} < \operatorname{arg} z \leq \frac{\pi}{n}\right\}. \tag{13.4} \end{equation*}
Observación 13.12.
No es difícil verificar que el dominio dado por (13.4) es mapeado bajo la función $f(z) = z^n$ en el conjunto $\mathbb{C}\setminus\{0\}$, para más detalle de este hecho se puede consultar la entrada 26 de esta unidad.
Notemos que si hacemos $k=0$ y $\theta = \operatorname{Arg}(z)$ en (13.2), entonces obtenemos una función que a cada $z\neq 0$ asigna únicamente una raíz cuadrada, la raíz principal.
Definición 13.5. (Raíz cuadrada principal.)
Sea $z\neq 0$. Definimos a la función raíz cuadrada principal como: \begin{equation*} f(z) = z^{1/2} = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right), \end{equation*} donde $r = |\,z\,|$ y $\theta = \operatorname{Arg}(z)$.
Debe ser claro que al tomar $\theta = \operatorname{Arg}(z)$ en la definición anterior estamos garantizando que los valores que tomará la función raíz cuadrada principal, es decir su imagen, serán los $z\neq 0$ tales que $-\pi < \operatorname{Arg}(z) \leq \pi$, el cual es un conjunto más grande que el dominio $D$ dado en (13.3.).
Ejemplo 13.8.
Obtengamos el valor de la raíz cuadrada principal de los puntos: $z_1 = -i$, $z_2 = -\sqrt{3}+i$ y $z_3 = 9$.
Solución.
a) Para $z_1 = -i$ tenemos que $|\,z_1\,| = 1$ y $\operatorname{Arg}(z_1) = -\frac{\pi}{2}$, por lo que: \begin{equation*} f(-i) = \sqrt{1} \operatorname{cis}\left(\frac{-\frac{\pi}{2}}{2}\right) = \operatorname{cos}\left(-\frac{\pi}{4}\right) + i \operatorname{cos}\left(-\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\left(1-i\right). \end{equation*} b) Para $z_2 = -\sqrt{3}+i$ tenemos que $|\,z_1\,| = 1$ y: \begin{equation*} \operatorname{Arg}(z_2) = \operatorname{arctan}\left(-\frac{1}{\sqrt{3}}\right) + \pi = \frac{5\pi}{6}, \end{equation*} por lo que: \begin{equation*} f\left(-\sqrt{3}+i\right) = \sqrt{2} \operatorname{cis}\left(\frac{\frac{5\pi}{6}}{2}\right) = \sqrt{2} \left[\operatorname{cos}\left(\frac{5\pi}{12}\right) + i \operatorname{sen}\left(\frac{5\pi}{12}\right)\right] = \frac{\sqrt{3} – 1}{2} + i \frac{\sqrt{3} + 1}{2}. \end{equation*} c) Para $z_1 = 9$ tenemos que $|\,z_3\,| = 9$ y $\operatorname{Arg}(z_1) = 0$, por lo que: \begin{equation*} f(9) = \sqrt{9} \operatorname{cis}\left(0\right) = 3\left[ \operatorname{cos}\left(0\right) + i \operatorname{sen}\left(0\right) \right] = 3. \end{equation*}
Ejemplo 13.9.
Veamos que la función $g(z) = z^{1/2}$, con $g$ la raíz cuadrada principal, es una inversa de la función $f(z) = z^2$ siempre que restrinjamos el dominio de $f$ al dominio $D$ dado por (13.3).
Solución. De acuerdo con el ejemplo 13.7 sabemos que la función $f(z) = z^2$ es inyectiva en el dominio $D$ dado por los $z\neq 0$ tales que $-\pi/2 < \operatorname{Arg}(z) \leq \pi/2$ y por la observación 13.12 tenemos que $f$ es biyectiva en $D$ y por tanto existe $f^{-1}$.
Procedemos ahora a verificar que $g(z) = z^{1/2}$, con $g$ la raíz cuadrada principal, es una inversa de $f$. Sean $z,w\neq 0$ y supongamos que $f^{-1}(z) = w$. Escribiendo a $z$ y $w$ en su forma polar tenemos que: \begin{equation*} z = r\operatorname{cis}(\theta), \quad w = \rho \operatorname{cis}(\alpha), \end{equation*} donde $r=|\,z\,|$, $\rho=|\,w\,|$, $\operatorname{Arg}(z) = \theta$ y $\operatorname{Arg}(w) = \alpha$.
Dado que el rango de $f^{-1}$ es el dominio de $f$, entonces el argumento principal de $w$, es decir $\alpha$, cumple que: \begin{equation*} -\frac{\pi}{2} < \alpha \leq \frac{\pi}{2}. \end{equation*}
Además, como $f(w) = w^2 = z$, entonces $w$ debe ser una de las dos raíces cuadradas dadas por (13.2), es decir $w = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right)$ ó $w = \sqrt{r} \operatorname{cis}\left(\frac{\theta + 2\pi}{2}\right)$.
Por reducción al absurdo supongamos que: \begin{equation*} w = f^{-1}(z) = \sqrt{r} \operatorname{cis}\left(\frac{\theta + 2\pi}{2}\right). \tag{13.5} \end{equation*}
Como $\operatorname{Arg}(z) = \theta$, entonces $-\pi < \theta \leq \pi$, por lo que:
\begin{equation*} \frac{\pi}{2} < \frac{\theta + 2\pi}{2} \leq \frac{3\pi}{2}. \tag{13.6} \end{equation*}
Tenemos que $\operatorname{Arg}(w) = \alpha$, entonces $\alpha \in (-\pi,\pi]$. Mientras que de (13.5) y (13.6) se sigue que $\pi/2 < \alpha \leq 3\pi/2$, por lo que $\pi/2 < \alpha \leq \pi$ ó $-\pi < \alpha \leq -\pi/2$. Sin embargo ninguna de estas condiciones se cumple desde $-\frac{\pi}{2} < \alpha \leq \frac{\pi}{2}$, por lo que nuestro supuesto en (13.5) es falso, entonces: \begin{equation*} w = f^{-1}(z) = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right), \end{equation*} la cual corresponde con la función $g(z) = z^{1/2}$ dada en la definición 13.5.
En general, considerando la observación 13.1, podemos definir una función que asigne una sola raíz, en particular la raíz $n$-ésima principal a cada $z\neq 0$, con $n\geq 2$.
Definición 13.6. (Raíz $n$-ésima principal.)
Sea $z\neq 0$. Para $n\geq 2$ definimos a la función raíz $n$-ésima principal como:
\begin{equation*} f(z) = z^{1/n} = \sqrt[n]{r} \operatorname{cis}\left(\frac{\theta}{n}\right), \end{equation*} donde $r = |\,z\,|$ y $\theta = \operatorname{Arg}(z)$.
Ejemplo 13.10.
De acuerdo con el ejemplo 13.1 sabemos que para la función multivaluada $F(z) = z^{1/3}$ se cumple que: \begin{equation*} F(1) = \left\{ 1, \frac{-1 + i\sqrt{3}}{2}, \frac{-1 – i\sqrt{3}}{2} \right\}. \end{equation*}
Mientras que si consideramos a la función raíz cúbica principal $f(z) = z^{1/3}$, entonces: $f(1) = 1$.
Observación 13.13.
De nueva cuenta, es importante mencionar que aunque la función raíz $n$-ésima principal, con $n\geq 2$, es una función univaluda, no necesariamente es una rama de la función multivaluada $F(z) = z^{1/n}$, pues como veremos en el ejemplo 15.7 de la entrada 15, la función raíz cuadrada principal $f(z)=z^{1/2}$ es discontinua en todo el eje real negativo desde que la función argumento principal es discontinua en dicho conjunto, el cual es un subconjunto del dominio $\mathbb{C}\setminus\{0\}$, correspondiente con el dominio de definición de dicha función.
De acuerdo con las observaciones 13.10 y 13.13 es interesante notar que podemos definir ramas de la función multivaluada $F(z) = z^{1/n}$, $n\geq 2$, de acuerdo con la definición 13.2, considerando ramas de la función multivaluada $G(z) = \operatorname{arg}(z)$, para ello solo debemos hacer uso de la definición 13.4. Más aún, dado un dominio donde esté definida la función $F$, entonces tendremos exactamente $n$ ramas diferentes para dicha función.
Para mostrar esto consideremos el siguiente:
Ejemplo 13.11.
Sea $ I = \left(\frac{3\pi}{2}, \frac{7\pi}{2}\right]$. Entonces, para $z\in\mathbb{C}\setminus L_{\frac{3\pi}{2}} = \left\{ z\in\mathbb{C} : |z|>0, \,\, \frac{3\pi}{2} <\operatorname{arg}(z)<\frac{7\pi}{2}\right\}$, podemos definir una rama de la función multivaluada $F(z) = z^{1/2}$, como: \begin{equation*} f_1(z) = z^{1/2} = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right), \end{equation*} donde $r = |\,z\,|$, $\theta = \operatorname{Arg}_I(z)$ y $L_{\frac{3\pi}{2}} = \left\{-ir : r\geq 0\right\}$, es decir la semirrecta imaginaria negativa que parte del origen.
Por el ejemplo 13.6 sabemos que para $z=i$ se tiene que: \begin{equation*} \operatorname{Arg}_{\left(\frac{3\pi}{2}, \frac{7\pi}{2}\right]}(i) = \frac{5\pi}{2}. \end{equation*}
Entonces: \begin{equation*} f_1(i) = \sqrt{1} \operatorname{cis}\left(\frac{5\pi}{4}\right) = -\frac{\sqrt{2}}{2} -i\frac{\sqrt{2}}{2}. \end{equation*}
Por otra parte, si utilizamos la función raíz cuadrada principal restringida al dominio $\mathbb{C}\setminus(-\infty, 0]$, es decir considerando el intervalo $I = (-\pi, \pi]$, tenemos: \begin{equation*} f_0(z) = z^{1/2} = \sqrt{r} \operatorname{cis}\left(\frac{\beta}{2}\right), \quad -\pi < \beta < \pi, \end{equation*} donde $r = |\,z\,|$, $\beta = \operatorname{Arg}(z)$ y $L{-\pi} = \left\{-r : r\geq 0\right\}$, la cual es llamada la rama principal.
Entonces para $z=i$ tenemos que $\operatorname{Arg}(z) = \frac{\pi}{2}$, por lo que:
\begin{equation*} f_0(i) = \sqrt{1} \operatorname{cis}\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}. \end{equation*}
Es claro que $f_0(i) \neq f_1(i)$, por lo que $f_0$ y $f_1$ son dos ramas diferentes de la función multivaluada $F(z) = z^{1/2}$.
Más aún, si tomamos $ I = \left(\pi, 3\pi\right]$, para para $z \in\mathbb{C}\setminus L_{\frac{3\pi}{2}} = \left\{ z\in\mathbb{C} : |z|>0, \,\, \pi <\operatorname{arg}(z)<3\pi\right\}$, podemos definir una tercera rama de la función multivaluada $F(z) = z^{1/2}$, como: \begin{equation*} f_2(z) = z^{1/2} = \sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right), \end{equation*} donde $r = |\,z\,|$, $\theta = \operatorname{Arg}_I(z)$ y $L{\pi} = \left\{-r : r\geq 0\right\}$.
Notemos que tanto $f_0$ como $f_2$ comparten el dominio $\mathbb{C}\setminus L_{\pi} = \mathbb{C}\setminus(-\infty, 0]$.
Para $z=i$ tenemos que $|\,i\,|=1$ y: \begin{equation*} \operatorname{Arg}_{(\pi, 3\pi]}(i) = \operatorname{Arg}\left(-i\operatorname{cis}(\pi)\right) + \pi + \pi = \operatorname{Arg}(i) + 2\pi = \frac{5\pi}{2}. \end{equation*}
Por lo que: \begin{equation*} f_2(i) = \sqrt{i} \operatorname{cis}\left(\frac{\frac{5\pi}{2}}{2}\right) = \operatorname{cis}\left(\frac{5\pi}{4}\right) = -\frac{\sqrt{2}}{2} -i\frac{\sqrt{2}}{2}. \end{equation*}
Desde que $f_0(i) \neq f_2(i)$, es claro que $f_0$ y $f_2$ son dos ramas diferentes de la función multivaluada $F(z) = z^{1/2}$. Sin embargo, puesto que $f_0$ y $f_2$ están definidas sobre el mismo dominio podemos obtener la siguiente relación.
Primeramente, procediendo como en la prueba de la proposición 13.3 es fácil verificar que: \begin{equation*} \operatorname{cis}\left(\theta+\beta\right) = \operatorname{cis}\left(\theta\right) \operatorname{cis}\left(\beta\right), \quad \forall \theta, \beta\in\mathbb{R}. \tag{13.7} \end{equation*}
Dado que $\theta\in (\pi, 3\pi)$ y $\beta \in (-\pi, \pi)$, entonces: \begin{equation*} \pi< \theta < 3\pi \quad \Longleftrightarrow \quad -\pi< \theta – 2\pi < \pi, \end{equation*} por lo que tomando $\beta= \theta – 2\pi$ tenemos que $\theta = \beta + 2\pi$.
Entonces, por (13.7) tenemos que: \begin{align*} f_2(z) &= \sqrt{r} \operatorname{cis}\left(\frac{\beta+2\pi}{2}\right)\\ & = \sqrt{r} \operatorname{cis}\left(\frac{\beta}{2} + \pi \right)\\ & = \sqrt{r} \operatorname{cis}\left(\frac{\beta}{2} \right) \operatorname{cis}\left(\pi \right)\\ & = – \sqrt{r} \operatorname{cis}\left(\frac{\beta}{2} \right),\quad -\pi< \beta < \pi, \end{align*} de donde se sigue que $f_0 = -f_2$.
Haciendo una analogía con el caso real, en el que hablábamos de la raíz positiva y la raíz negativa de un número real positivo, podemos pensar a las ramas $f_0$ y $f_2$, de la función multivaluada $F(z) = z^{1/2}$, como la raíz positiva y negativa de un número complejo.
Observación 13.14.
De acuerdo con lo anterior, debe ser claro que la función multivaluada $F(z)=z^{1/2}$ está completamente determinada por sus dos ramas, es decir, una vez elegida una rama del argumento, entonces $F$ está dada por sus ramas positiva y negativa.
Sea $z=r\operatorname{cis}(\theta) \neq 0$, con $r=|z|>0$ y $\theta = \operatorname{arg}(z) = \theta_I + 2\pi n$, para $n\in\mathbb{Z}$, $\theta_I = \operatorname{Arg}_{I}(z) \in I$ e $I$ un intervalo de longitud $2\pi$, definición 13.4. Entonces: \begin{align*} F(z) = z^{1/2} & = \left(r\operatorname{cis}(\theta)\right)^{1/2}\\ & = \sqrt{r}\operatorname{cis}\left(\frac{\theta}{2}\right)\\ & = \sqrt{r}\operatorname{cis}\left(\frac{\theta_I}{2} + \pi n\right)\\ & = \sqrt{r}\operatorname{cis}\left(\frac{\theta_I}{2} \right) \operatorname{cis}\left(\pi n\right), \quad n\in\mathbb{Z}. \end{align*}
Considerando los resultados de la entrada 5, sabemos que únicamente $n=0$ y $n=1$ determinan valores distintos para $F$, ya que si $n$ es par obtenemos el mismo valor que $n=0$ y si $n$ es impar obtenemos el mismo valor que $n=1$, es decir que para otros valores enteros de $n$ obtenemos los mismos valores para $F$ que los dados por $n=0$ y $n=1$. Entonces: \begin{equation*} F(x)= \left\{ \begin{array}{lcc} \sqrt{r}\operatorname{cis}\left(\frac{\theta_I}{2} \right) & \text{si} & n=0,\\ \\- \sqrt{r}\operatorname{cis}\left(\frac{\theta_I}{2} \right) & \text{si} & n=1, \end{array} \right. \end{equation*} con $\theta_I \in I$. Es decir, estos dos valores distintos de $F$ determinan sus dos ramas.
Por ejemplo si elegimos a la rama principal del argumento, es decir $\theta_I = \operatorname{Arg}(z)$ con $I = (-\pi, \pi]$, entonces para $z=r\operatorname{cis}\left(\theta_I\right) \neq 0$ tenemos que: \begin{equation*} F(z) = f_{\pm}(z) = \pm \sqrt{r} \operatorname{cis}\left(\frac{\theta_I}{2}\right), \quad -\pi < \theta_I < \pi. \end{equation*}
Cerraremos esta entrada con dos nuevos conceptos que también juegan un papel importante al trabajar con funciones multivaluadas, los cuales utilizaremos más adelante.
Definición 13.6.(Punto de ramificación.)
Sea $F(z)$ una función multivaluada definida en un dominio $D\subset\mathbb{C}$ y sea $z_0 \in \mathbb{C}$. Decimos que $z_0$ es un punto de ramificación de $F$ si una vuelta alrededor de $z_0$ (y suficientemente cerca a $z_0$) produce un cambio de rama de la función.
Si $n$ es el menor número natural tal que $n$ vueltas alrededor de $z_0$ llevan cada rama sobre sí misma, decimos que $z_0$ es un punto de ramificación de orden $n-1$. Si nunca vuelve a la rama original, diremos que es de orden $\infty$. El punto al infinito $z_\infty = \infty$ es un punto de ramificación de $F(z)$ si una vuelta alrededor de una circunferencia suficientemente grande provoca un cambio de rama. Equivalentemente, $z_\infty = \infty$ es un punto de ramificación de $F(z)$ si $z = 0$ es un punto de ramificación de la función $F(1/z)$.
Ejemplo 13.12.
Consideremos a la función multivaluada $F(z) = z^{1/2}$. Veamos que $z_0=0$ y $z_\infty = \infty$ son puntos de ramificación de $F$.
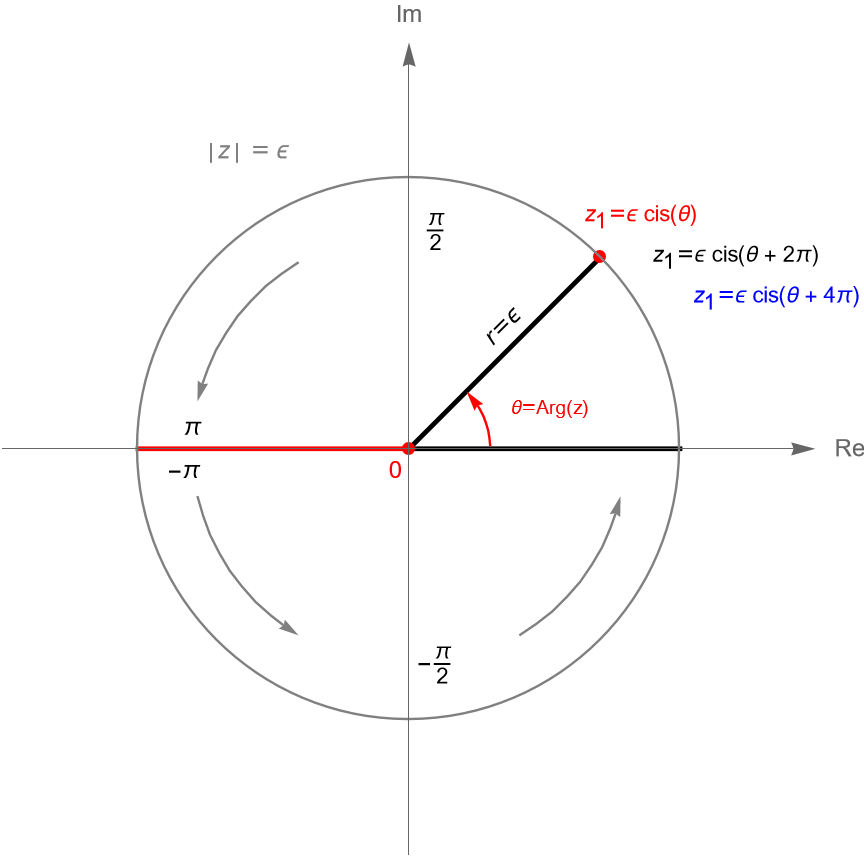
Solución. Es claro que la función $F$ no está definida para $z=0$, por lo que no es casualidad que dicho punto sea una punto de ramificación de $F$. Sea $C(z_0,\varepsilon)$ una circunferencia con centro en $z_0=0$ y radio $\varepsilon>0$, con $\varepsilon$ arbitrariamente pequeño. Sabemos que un punto $z\in C(z_0,\varepsilon)$ en su forma polar está dado por: \begin{equation*} z = \varepsilon \operatorname{cis}(\theta), \quad -\pi < \theta \leq \pi, \end{equation*} donde $\theta = \operatorname{Arg}(z)$ y $\varepsilon = |\,z\,|$.
De acuerdo con la observación 13.14, sabemos que la función multivaluada $F(z) = z^{1/2}$ tienes dos ramas diferentes, su rama positiva y su rama negativa, es decir $f_{+}$ y $f_{-}$. Supongamos que a $z_1 \in C(z_0,\varepsilon)$ le hemos aplicado $F$, entonces tenemos que: \begin{equation*} F(z_1) = \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta}{2}\right) = f_+(z_1), \quad -\pi < \theta <\pi. \end{equation*}
Si consideramos que $z_1$ ha dado una vuelta completa sobre la circunferencia $C(z_0,\varepsilon)$, en el sentido contrario al de las manecillas del reloj, es decir que $\theta$ aumento $2\pi$, entonces tenemos que: \begin{align*} F(z_1) & = \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta+2\pi}{2}\right)\\ & = \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta}{2}\right) \operatorname{cis}\left(\pi\right)\\ &= – \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta}{2}\right), \quad -\pi < \theta <\pi,\ & = – f_+(z_1)\\ & = f_{-}(z_1), \end{align*} es decir, al partir de un punto arbitrario sobre la circunferencia $C(z_0,\varepsilon)$ y dar una vuelta completa sobre dicha circunferencia la función multivaluada $F(z)=z^{1/2}$ cambio de rama, por lo que $z_0 =0$ es un punto de ramificación de dicha función, figura 62.
Notemos que si $z_1$ da dos vueltas completas sobre la circunferencia $C(z_0,\varepsilon)$, es decir $ 3\pi < \theta + 4\pi < 5\pi$, entonces: \begin{align*} F(z_1) & = \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta+4\pi}{2}\right)\\ & = \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta}{2}\right) \operatorname{cis}(2\pi)\\ & = \sqrt{\varepsilon} \operatorname{cis}\left(\frac{\theta}{2}\right), \quad -\pi<\theta<\pi,\\ & = f_+(z_1), \end{align*} por lo que, después de dos vueltas completas alrededor del punto $z_0 = 0$ el valor de la función multivaluada $F$ regresa al valor de la rama principal $f_0$, es decir a su rama positiva, entonces $z_0 = 0$ es un punto de ramificación de orden $1$.
Recordemos que en la esfera de Riemann el punto al infinito $z_\infty=\infty$ corresponde con el polo norte $N$. Por lo que una circunfernecia alrededor de $N$, de radio arbitrariamente pequeño sobre la esfera de Riemann, determina una circunferencia de radio muy grande en el plano complejo. Esta curva rodea, necesariamente, a $z_0=0$. Por lo tanto, una vuelta completa sobre esta circunferencia causará un cambio de rama de la función multivaluada $F(z) = z^{1/2}$.
Procediendo como antes, podemos concluir fácilmente que $z_\infty = \infty$ también es un punto de ramificación de orden $1$ de $F$.
Sea $z = r\operatorname{cis}(\theta) \neq 0$, con $\theta = \operatorname{Arg}(z)$ y $r=|\,z\,|$. Notemos que $F(1/z) = \left(z^{-1}\right)^{1/2} = z^{-1/2}$, entonces: \begin{align*} F\left(\frac{1}{z}\right) & = \left(z\right)^{-1/2}\\ & = \left(\sqrt{r} \operatorname{cis}\left(\frac{\theta}{2}\right)\right)^{-1}\\ & = r^{-1/2} \operatorname{cis}\left(-\frac{\theta}{2}\right), \quad -\pi<\theta<\pi,\\ & = f_{+}\left(\frac{1}{z}\right). \end{align*}
Tomemos un punto $z$ sobre la circunferencia $C(z_0,\varepsilon)$, con $z_0 =0$ y $\varepsilon>0$ arbitrariamente pequeño. Si $z$ da una vuelta completa alrededor de $z_0$ tendremos que $\theta$ habrá aumentado $2\pi$, por lo que: \begin{align*} F\left(\frac{1}{z}\right) & = r^{-1/2} \operatorname{cis}\left(\frac{-\theta + 2\pi}{2}\right)\\ & = r^{-1/2} \operatorname{cis}\left(-\frac{\theta}{2}\right) \operatorname{cis}\left(\pi\right)\\ & = r^{-1/2} \operatorname{cis}\left(-\frac{\theta}{2}\right) \operatorname{cis}\left(\pi\right)\\ & = -r^{-1/2} \operatorname{cis}\left(-\frac{\theta}{2}\right), \quad -\pi<\theta<\pi,\\ & = f_{-}\left(\frac{1}{z}\right). \end{align*}
Entonces, después de una vuelta alrededor del punto $z_0=0$, la función multivaluada $F(1/z)$ cambio de rama, por lo que $z=0$ es un punto de ramificación de $F(1/z)$ y por tanto $z_\infty = \infty$ es un punto de ramificación de $F(z)$.
De manera análoga, si $z$ da dos vueltas alrededor de $z_0 = 0$, entonces $F$ vuelve a tomar el valor de la rama principal, es decir que con dos vueltas la rama principal regresa a sí misma, por tanto $z_0$ es un un punto de ramificación de orden $2-1 = 1$ de $F(1/z)$.
Definición 13.6.(Corte de rama.)
Un corte de rama es una línea (habitualmente recta) que separa dos ramas de una misma función multivaluada. Equivalentemente, es la línea en la que una rama se hace discontinua.
Observación 13.15.
Los cortes de rama son, en realidad, curvas por las que hacemos discontinuas las ramas y que impiden que podamos dar una vuelta completa alrededor de un punto de ramificación. Es muy importante hacer notar que los cortes de rama no son únicos y podemos elegirlos según nos convenga.
Ejemplo 13.13.
Consideremos a la función multivaluada $F(z) = z^{1/2}$. De acuerdo con el ejemplo 13.11, tenemos que para las ramas $f_0, f_1$ y $f_2$ sus cortes de ramas son, respectivamente, las semirrectas: \begin{align*} L_{-\pi} = \left\{-r : r\geq 0\right\} = (-\infty,0],\\ L_{\frac{3\pi}{2}} = \left\{-ir : r\geq 0\right\},\\ L_{\pi} = \left\{-r : r\geq 0\right\} = (-\infty,0], \end{align*} pues en dichos conjuntos cada una de las ramas no son continuas.
Ejemplo 13.14.
Consideremos a \begin{equation*} I = \left(\frac{3\pi}{2}, \frac{7\pi}{2}\right]. \end{equation*}
La función $\operatorname{Arg}_I(z)$ es discontinua en: \begin{equation*} L_{\frac{3\pi}{2}} = \left\{-ir : r\geq 0\right\}, \end{equation*} por lo que dicha semirrecta corresponde con su corte de rama.
Por otra parte, para la función $\operatorname{Arg}(z)$ se tiene que su corte de rama es la semirrecta: \begin{equation*} L_{-\pi} = \left\{-r : r\geq 0\right\} = (-\infty,0], \end{equation*} pues en dicho conjunto la función es discontinua.
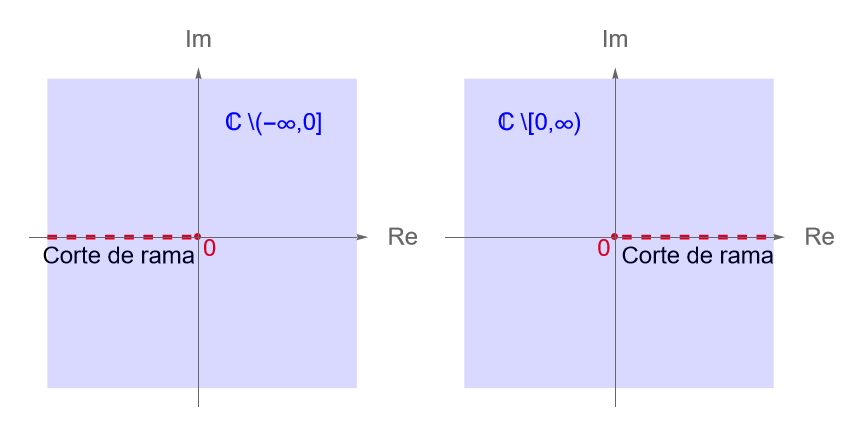
Ejemplo 13.15.
Considerando las ramas principal y natural del argumento determina los corte de rama para la función multivaluada $F(z) = \sqrt{z^2-1}$. ¿Cuáles son los puntos de ramificación de $F$?
Solución. Sabemos que para la función multivaluada $F(w)=\sqrt{w}$, se tiene que $w=0$ y $w=\infty$ son ambos puntos de ramificación de orden 1, por lo que si $w=z^2-1$, entonces un primer candidato a ser punto de ramificación es $w=0$, es decir, $z^2-1=(z-1)(z+1) = 0$, de donde inferimos que $z=1$ y $z=-1$ son ambos puntos de ramificación.
Sean:
\begin{equation*}
z-1=r_1 \operatorname{cis}(\alpha_1), \quad r_1 = |\,z-1\,|, \,\, \operatorname{arg}(z-1) = \alpha_1,
\end{equation*}
\begin{equation*}
z+1=r_2 \operatorname{cis}(\alpha_2), \quad r_2 = |\,z+1\,|, \,\, \operatorname{arg}(z+1) = \alpha_2,
\end{equation*}donde $\alpha_1 = \theta_1 +2\pi n_1$, $\alpha_2 = \theta_2 +2\pi n_2$ con $\theta_1 = \operatorname{Arg}(z-1)$, $\theta_2 = \operatorname{Arg}(z+1)$ y $n_1, n_2 \in \mathbb{Z}$.
Entonces, considerando la proposición 13.2 tenemos que:
\begin{align*}
z^2-1 = (z-1)(z+1) & = r_1 r_2\operatorname{cis}\left(\alpha_1 + \alpha_2\right)\\
& = r_1 r_2\operatorname{cis}\left(\theta_1 + \theta_2 + 2n\pi\right), \quad n = n_1+n_2 + N_{+}\in\mathbb{Z},
\end{align*}con $N_{+} \in \{-1, 0, 1\}$.
Por lo que:
\begin{align*}
F(z) = \sqrt{(z-1)(z+1)} & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1 + \theta_2}{2} + n\pi\right)\\
& = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1 + \theta_2}{2}\right)\operatorname{cis}\left(n\pi\right), \quad n\in\mathbb{Z}.
\end{align*}
De acuerdo con la observación 3.14, es claro que las dos ramas diferentes de $F$ están dadas para los valores enteros $n=0$ y $n=1$.
Para $n=0$ tenemos:
\begin{equation*}
f_{+}(z) = \sqrt{z^2 -1} = \sqrt{(z-1)(z+1)} = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1+\theta_2}{2}\right).
\end{equation*}
Y para $n=1$ tenemos:
\begin{equation*}
f_{-}(z) = \sqrt{z^2 -1} = \sqrt{(z-1)(z+1)} = -\sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1+\theta_2}{2}\right).
\end{equation*}
En ambos casos $r_1, r_2 >0$ y $-\pi < \theta_1, \theta_2 <\pi$.
Si elegimos la rama principal del argumento, entonces tenemos que:
\begin{equation*}
-\pi < \operatorname{Arg}(w)\leq \pi \quad \Longleftrightarrow \quad \left\{w\in\mathbb{C} : \operatorname{Re}(w)\leq 0, \operatorname{Im}(w) = 0 \right\}.
\end{equation*}
Por lo que, tomando $z=x+iy\in\mathbb{C}$ y $w = z^2-1$, con $x,y\in\mathbb{R}$, tenemos que el corte de rama de la rama principal $f_0(z) = \sqrt{z^2-1}$ está dado por las siguientes condiciones:
\begin{equation*}
\left\{ \begin{array}{l}
\operatorname{Re}(z^2-1) = x^2 – y^2 -1 \leq 0,\\
\\ \operatorname{Im}(z^2-1) = 2xy = 0.
\end{array}
\right.
\end{equation*}
De la segunda condición es claro que puede sucder que $x=0$ ó $y=0$. Si $x=0$, entonces de la primera condición se sigue que $y^2 +1 \geq 0$, lo cual se cumple para todo $y\in\mathbb{R}$.
Por otra parte, si $y=0$, entonces de la primera condición se sigue que $x^2 \leq 1$, lo cual se cumple para todo $x\in\mathbb{R}$ tal que $|\,x\,| \leq 1$.
Entonces, considerando la rama principal del argumento, tenemos que el corte de rama de $f_0$ es:
\begin{equation*}
L_P = \left\{z =x+iy\in\mathbb{C} : x=0, y \in\mathbb{R} \right\} \cup \left\{z =x+iy\in\mathbb{C} : |\,x\,| \leq 1, y = 0 \right\}.
\end{equation*}
El conjunto anterior corresponde con todo el eje imaginario y el intervalo real $[-1,1]$, sin embargo, geométricamente podemos notar que el primer conjunto de discontinuidades para la rama principal $f_0$ se puede omitir desde que dicho conjunto ya se considera si definimos a dicha rama como:
\begin{equation*}
f_0(z) = \sqrt{z^2-1} = \left\{ \begin{array}{lcc}
f_+(z) & \text{si} & \operatorname{Re}(z)>0,\\
\\ f_-(z) & \text{si} & \operatorname{Re}(z)<0,
\end{array}
\right.
\end{equation*}cuyo corte de rama, para cada función, es respectivamente:
\begin{equation*}
\left\{z =x+iy\in\mathbb{C} : y=0, 0<x\leq 1 \right\} \quad \text{y} \quad \left\{z =x+iy\in\mathbb{C} : y=0, -1 \leq x <0 \right\}.
\end{equation*}
Por tal motivo, resulta completamente innecesario mencionar a las discontinuidades del eje imaginario, pues están implícitas en la definición de la rama principal dada antes, por ello, al hablar del corte de rama para esta función bastará con mencionar al intervalo real $[-1,1]$, es decir:
\begin{equation*}
L_P = \left\{z =x+iy\in\mathbb{C} : |\,x\,| \leq 1, y = 0 \right\}.
\end{equation*}
Por otra parte, si elegimos la rama natural del argumento entonces tenemos que:
\begin{equation*}
0 \leq \operatorname{Arg}(w) < 2\pi \quad \Longleftrightarrow \quad \left\{w\in\mathbb{C} : \operatorname{Re}(w)\geq 0, \operatorname{Im}(w) = 0 \right\}.
\end{equation*}
Por lo que, tomando $w = z^2-1$ y $z=x+iy$, con $x,y\in\mathbb{R}$, tenemos que el corte de rama de la rama $f(z) = \sqrt{z^2-1}$ está dado por las condiciones:
\begin{equation*}
\left\{ \begin{array}{l}
\operatorname{Re}(z^2-1) = x^2 – y^2 -1 \geq 0,\\
\\ \operatorname{Im}(z^2-1) = 2xy = 0.
\end{array}
\right.
\end{equation*}
De manera análoga concluimos que $x\neq 0$, por lo que de la segunda condición se sigue que $y=0$, entonces $x^2\geq 1$, es decir $|\,x\,| \geq 1$.
Entonces, considerando la rama natural del argumento, tenemos que el corte de rama de $f$ son dos semirrectas dadas por:
\begin{equation*}
L_N = \left\{z =x+iy\in\mathbb{C} : |\,x\,| \geq 1, y = 0 \right\}.
\end{equation*}
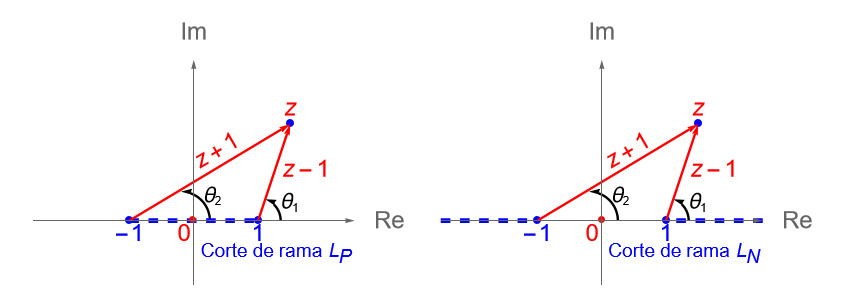
De lo anterior es claro que los puntos $z=1$ y $z=-1$ aparecen en ambos cortes de rama, por lo que procedemos a verificar que son puntos de ramificación de la función multivaluada $\sqrt{z^2-1}$.
Consideremos una circunferencia con centro en $1$ y radio suficientemente pequeño para que el punto $z=-1$ sea un punto exterior a ella, figura 65, y tomemos a un punto cualquiera $z$ sobre ella, entonces:
\begin{equation*}
F(z) = \sqrt{z^2 -1} = \sqrt{(z-1)(z+1)} = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1+\theta_2}{2}\right) = f_{+}(z).
\end{equation*}
Notemos que si damos una vuelta alrededor del punto $z=1$, considerando el punto $z$ sobre la circunferencia dada, entonces solo el argumento de $z-1$ se verá afectado, es decir:
\begin{align*}
F(z) & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\left(\theta_1 + 2\pi\right) +\theta_2}{2}\right)\\
& = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1+\theta_2}{2}\right) \operatorname{cis}\left(\pi\right)\\
& = – \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1 +\theta_2}{2}\right)\\
& = f_{-}(z)\\
& \neq f_{+}(z),
\end{align*}por lo que, después de una vuelta alrededor del punto $z=1$, la función $F$ cambió de rama, es decir que $z=1$ es un punto de ramificación de orden $1$.
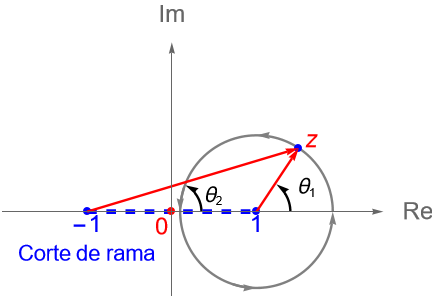
De manera similar, si tomamos un punto $z$ sobre una circunferencia con centro en el punto $z=-1$ y radio suficientemente pequeño de tal forma que el punto $z=1$ sea un punto exterior a ella, figura 66, entonces el argumento de $z+1$ se verá modificado en $2\pi$, es decir: \begin{align*} F(z) & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\left(\theta_2 + 2\pi\right) +\theta_1}{2}\right)\\ & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1+\theta_2}{2}\right) \operatorname{cis}\left(\pi\right)\\ & = – \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1 +\theta_2}{2}\right)\\ & = f_1(z)\\ & \neq f_0(z), \end{align*} por lo que, de nueva cuenta la función $F$ cambio de rama, entonces $z=-1$ también es un punto de ramificación de orden $1$.
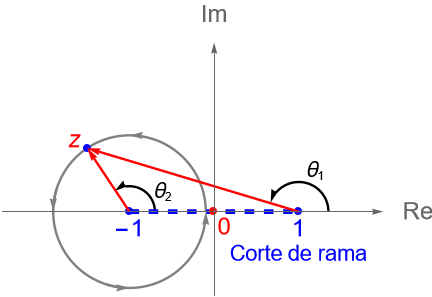
Por último, tomemos a un punto $z_0\in\mathbb{C}$, con $z_0 \neq 1, -1$, y tracemos una circunferencia con centro en $z_0$ y radio suficientemente pequeño, de tal forma que $1$ y $-1$ sean puntos exteriores a ella, figura 67. Notemos que si un punto $z$ da una vuelta completa sobre dicha circunferencia, entonces los argumentos de $z-1$ y $z+1$ no se ven modificados, por lo que la función $F$ no cambia de rama, es decir que $z_0$ no es un punto de ramificación, por lo que $z=1$ y $z=-1$ son los únicos puntos de ramificación.
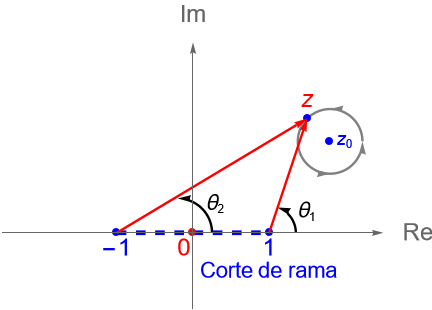
Más aún, si tomamos una circunferencia que encierre a ambos puntos de ramificación, al dar una vuelta completa sobre dicha circunferencia tendremos que tanto el argumento de $z-1$ como el de $z+1$ se verán modificados, es decir: \begin{align*} F(z) & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\left(\theta_1 + 2\pi\right) + \left(\theta_2 + 2\pi\right)}{2}\right)\\ & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1+\theta_2}{2}\right) \operatorname{cis}\left(2\pi\right)\\ & = \sqrt{r_1 r_2} \operatorname{cis}\left(\frac{\theta_1 +\theta_2}{2}\right), \end{align*} de donde se sigue que $z=\infty$ no es un punto de ramificación.
Es sencillo verificar esto último considerando a la función $F(1/z)$, por lo que se deja como ejercicio al lector.
Gráficamente, los cortes de rama dados en la figura 64 nos aseguran que una rama definida en un dominio que excluya a dichos conjuntos en efecto será una función continua univaluada, es decir, solo nos determinará un único valor para cada $z$ en dicho dominio.
Tarea moral
- Verifica que se cumple la observación 13.3.
- Demuestra la proposición 13.2.
- Obtén, en las regiones apropiadas, las funciones inversas $z=g(w)$ de:
a) $w = f(z) = z^3$.
b) $w = f(z) = (z-1)^4+i$.
c) $w = f(z) = z^7+1+i$.
d) $w = f(z) = 2z^2+iz-i+1$. - Verifica que se cumple (13.7).
- Considera a la función multivaluada $F(z) = z^{1/3}$ dada por sus tres ramas $f_0, f_1$ y $f_2$ siguientes: \begin{equation*} F(z) = \left\{ \begin{array}{lcc} f_0(z) = \sqrt[3]{r}\operatorname{cis}\left(\frac{\theta}{3}\right) & \text{si} & 0 \leq \theta < 2\pi, \\ f_1(z) = \sqrt[3]{r}\operatorname{cis}\left(\frac{\theta}{3}\right) & \text{si} & 2\pi \leq \theta < 4\pi, \\ f_2(z) = \sqrt[3]{r}\operatorname{cis}\left(\frac{\theta}{3}\right) & \text{si} & 4\pi \leq \theta < 6\pi, \end{array} \right. \end{equation*} donde $\theta = \operatorname{Arg}_{[0,2\pi)}(z)$ y $r=|\,z\,|$.
Prueba que $z_0 = 0$ y $z_\infty = \infty$ son puntos de ramificación de $F$, ambos de orden $2$. - Muestra que los puntos dados son los puntos de ramificación de las siguientes funciones multivaluadas.
a) $z=0$, $z=\infty$ ambos de orden $n-1$ para $F(z) = \sqrt[n]{z}$, $n\geq 2$. Recuerda que para esta función existen exactamente $n$ ramas distintas.
b) $z=5$, $z=i$ y $z=2i-3$, los tres de orden $1$ para $F(z) = \sqrt{(z-5)(z-i)(z-2i+3)}$. - Prueba que el corte de rama de la función $f(z) = \operatorname{Arg}(iz-1)$ es la semirrecta: \begin{equation*} L = \left\{z=x+iy\in\mathbb{C} : x=0, y\geq 0\right\} \end{equation*} Hint: Observa que $-\pi < \operatorname{Arg}(w) \leq \pi \quad \Longleftrightarrow \quad \left\{w\in\mathbb{C} : \operatorname{Re}(w)\leq 0, \operatorname{Im}(w)=0\right\}$.
- Sean $\alpha\in\mathbb{R}$ e $I = (\alpha, \alpha+2\pi]$. Define: \begin{equation*} \alpha^* = \alpha – 2\pi\left(\left\lceil\frac{\alpha}{2\pi}\right\rceil – 1 \right). \end{equation*} Muestra que: \begin{equation*} \operatorname{Arg}_I(z) = \left\{ \begin{array}{lcc} \operatorname{Arg}(z) + 2\pi\left( \left\lceil\frac{\alpha}{2\pi}\right\rceil – 1\right) & \text{si} & \alpha^*< \operatorname{Arg}(z) \leq \pi, \\ \operatorname{Arg}(z) + 2\pi \left\lceil\frac{\alpha}{2\pi}\right\rceil & \text{si} & \alpha^*< \operatorname{Arg}(z) \leq \pi, \end{array} \right. \end{equation*} donde $\lceil x \rceil = n \quad \Longleftrightarrow \quad n-1<x\leq n \quad \Longleftrightarrow \quad x \leq n < x+1$, para $n\in\mathbb{Z}$.
Más adelante…
En esta entrada introducimos de manera formal el concepto de función multivaluada y vimos algunos ejemplos puntuales de funciones de este tipo considerando algunos resultados que habíamos obtenido a lo largo de la unidad anterior.
En resumen, una función multivaluada puede pensarse como una colección de funciones univaluadas a las cuales llamamos ramas de la función. Más aún, las funciones multivaluadas pueden caracterizarse por sus puntos de ramificación y sus cortes de ramas. Los cortes de ramas, nos definen una rama de la función multivaluada, de acuerdo con la definición 13.2, la cual es una función discontinua sobre los puntos del corte ramal.
Dado que cada corte de rama impone una restricción en los valores del argumento, los cuales están limitados a un intervalo de longitud $2\pi$, y a su vez cada rama del argumento implica un corte en el plano complejo, entonces no existe una única forma de definir un corte de rama, esto dependerá en esencia de las necesidades del cálculo en cierto problema.
En las siguientes entradas estaremos trabajando con más ejemplos de funciones multivaluadas, como el logaritmo y las funciones inversas de las funciones trigonométricas e hiperbpolicas, que resultan ser de las funciones más elementales para el caso complejo, por lo que es importante familiarizarnos con este nuevo concepto y con las propiedades que lo definen.
La siguientes dos entradas veremos dos conceptos fundamentales en la teoría de las funciones, el del límite y continuidad. Como vimos en nuestros cursos de Cálculo, es posible estudiar y caracterizar a una función real a través del límite y la continuidad en un punto de la misma. Nuestro objetivo en las siguientes entradas consistirá en trabajar dichos conceptos pero desde la perspectiva de la variable compleja.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Funciones de variable compleja. Definiciones y preliminares.
- Siguiente entrada del curso: Límites en $\mathbb{C}$.