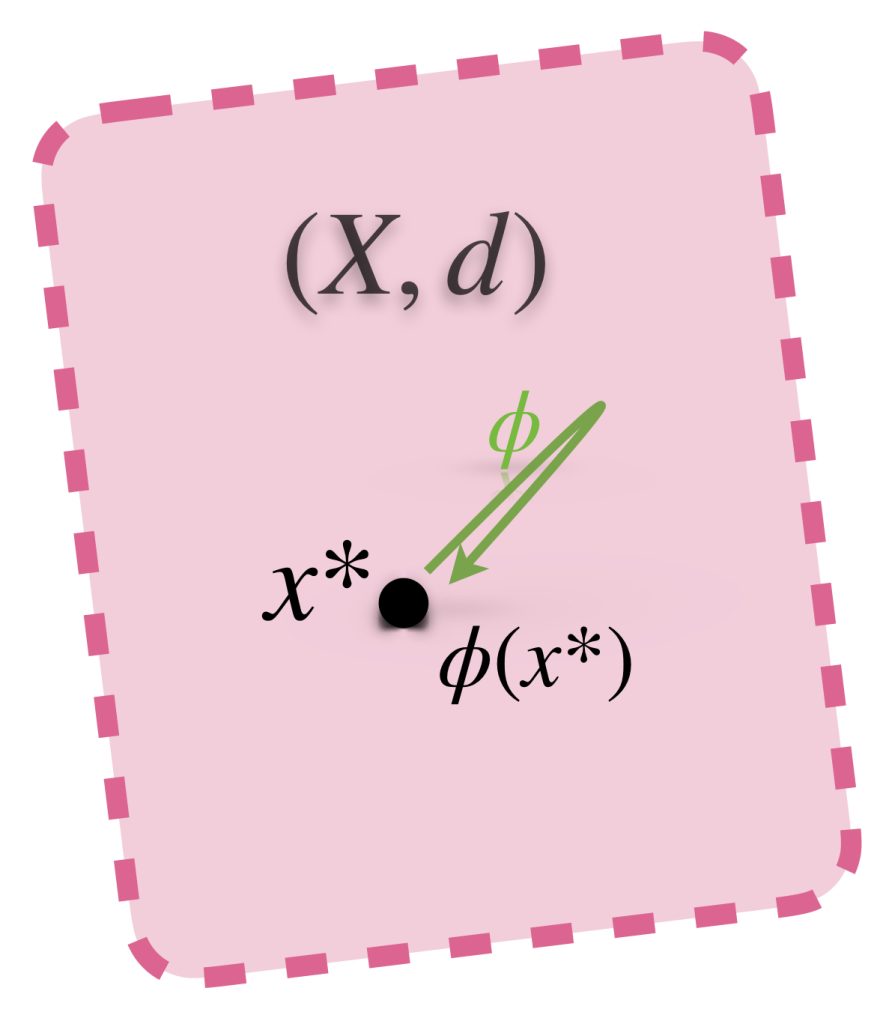Introducción

Cuando los puntos de un espacio métrico son enviados al mismo espacio a través de una función, conviene saber si habrá algún punto que se envíe a sí mismo, es decir, que se conserve fijo. Las próximas entradas nos mostrarán cuándo esa situación ocurre y resultados interesantes derivados de ello. Comencemos con la primera:

Definición. Función contracción: Sea $(X,d)$ un espacio métrico y $ \phi: X \to X$ una función. Diremos que $\phi$ es una contracción si existe $\alpha \in (0,1)$ tal que para cualesquiera $x,y \in X$ se cumple que:
$$d(\phi(x),\phi(y)) \leq \alpha \, d(x,y)$$

Podemos pensar entonces, que una función contracción, justamente hace que los puntos sean más cercanos entre sí de lo que eran originalmente.

Nota que una contracción es también una función Lipschitz continua con constante de Lipschitz $c<1.$ Este concepto se vio en la entrada Más conceptos de continuidad. Demos paso a otra:

Definición. Punto fijo: Sea $X$ un espacio métrico y $x^* \in X.$ Decimos que $x^*$ es punto fijo de la función $\phi:X \to X$ si $\phi(x^*)=x^*.$

Para ejemplificar estas ideas, veamos dos funciones que son contracciones y cómo existe un punto fijo en los casos a mencionar:

Ejemplos. $f(x)=\dfrac{x}{2},$ con $\alpha = \dfrac{1}{2}.$

Considera $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=\dfrac{x}{2}$ en el espacio euclidiano. Sean $x,y \in \mathbb{R}.$ Sucede que:

\begin{align*}
d(f(x),f(y))&=|f(x)-f(y)| \\
&=\left|\frac{x}{2}-\frac{y}{2} \right| \\
&=\left|\frac{1}{2}(x-y) \right| \\
&=\frac{1}{2}|x-y| \\
&=\frac{1}{2}d(x,y)
\end{align*}

Por lo tanto $d(f(x),f(y)) \leq \frac{1}{2}d(x,y)$ lo que demuestra que $f$ es una contracción con $\alpha = \frac{1}{2}$.

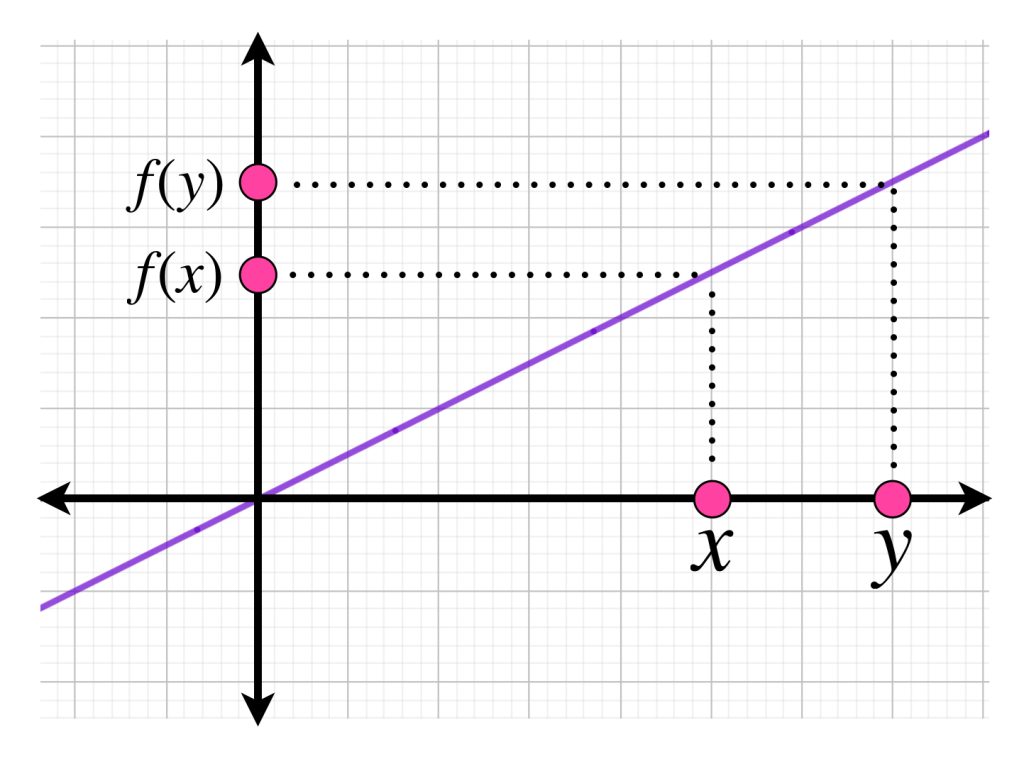
La siguiente imagen representa la diferencia de las distancias antes y después de aplicar la función en dos puntos $x$ y $y.$ Basta con observar las proyecciones de la gráfica de $f$ en los ejes coordenados.

Ahora busquemos un punto fijo:

\begin{align*}
f(x)&=x \\
\iff \frac{x}{2}&=x \\
\iff x&=2x \\
\iff 0&=2x-x \\
\iff 0&=x
\end{align*}

Es decir, $0$ es el único punto fijo de $f.$

A continuación, vamos a construir una sucesión de la siguiente manera:

Toma cualquier $x_0 \in X$

$x_1:=f(x_0)=\dfrac{x_0}{2}$

$x_2 :=f(x_1)=\dfrac{\dfrac{x_0}{2}}{2}=\dfrac{x_0}{2^2}$

$x_3:=f(x_2)=\dfrac{\dfrac{x_0}{2^2}}{2}=\dfrac{x_0}{2^3}$
.
.
.
$x_k:=f(x_{k-1})=\dfrac{x_0}{2^k}$

Entonces la sucesión se define como $(x_n)_{n \in \mathbb{N}} \, $ donde $x_n = \dfrac{x_0}{2^n}.$
Nota que tiende a $0$ en $\mathbb{R}.$

En las siguientes gráficas podemos observar el comportamiento de la sucesión:

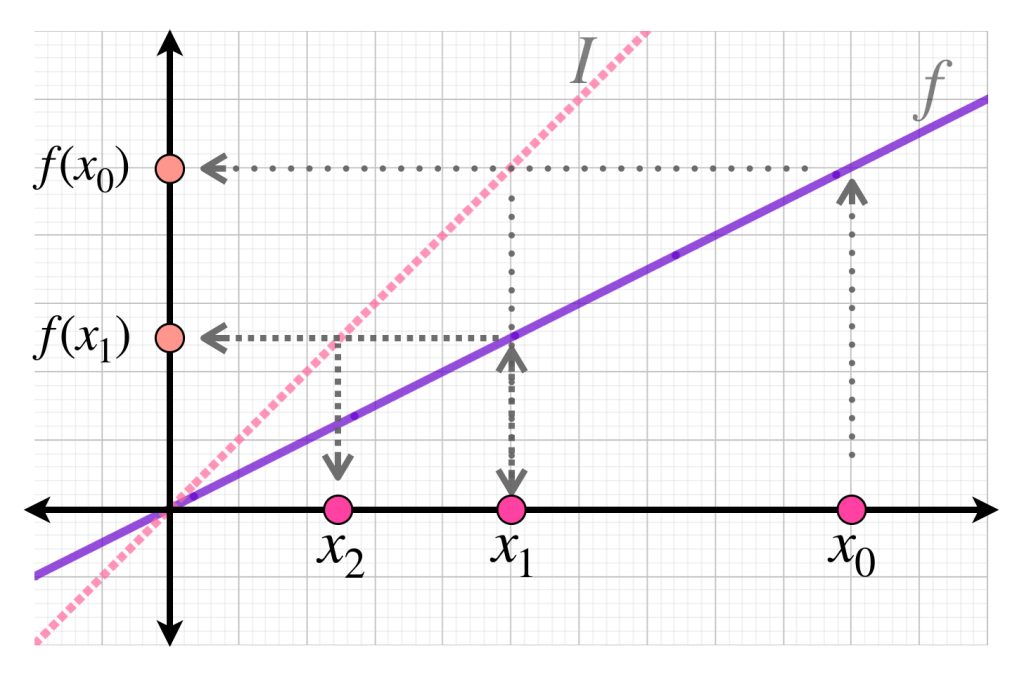
Sea $x_0 \in X.$ Mostramos la gráfica de la función $f(x)=\dfrac{x}{2}$ y la función identidad $ \, \mathcal{I}(x)=x.$
Señalamos los términos $x_0$ y $x_1 =f(x_0)=\dfrac{x_0}{2}$ y la distancia entre $f(x_0) \,$ y $\, f(x_1)$ vistos como proyecciones de las gráficas de los puntos sobre los ejes del plano cartesiano:

Si continuamos, generamos el punto $x_2=f(x_1).$ Gráficamente también es visible que las distancias entre dos puntos disminuyen en el eje vertical al continuar con las iteraciones.

Podemos observar que los puntos convergen a $0$ que recordemos, es también el punto fijo de $f$.

Veamos otro caso:

Ejemplo. $f(x)=\dfrac{x}{2}+6,$ con $\alpha = \dfrac{1}{2}.$

Considera $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=\dfrac{x}{2}+6$ en el espacio euclidiano. Sean $x,y \in \mathbb{R}.$ Sucede que:

\begin{align*}
|f(x)-f(y)|&=\left|\frac{x}{2}+6- \left(\frac{y}{2}+6 \right) \right| \\
&= \left|\frac{1}{2}(x-y) \right| \\
&= \frac{1}{2}|x-y|
\end{align*}

De modo que $d(f(x),f(y))\leq \frac{1}{2}d(x,y)$ lo cual prueba que $f$ es una contracción con $\alpha = \frac{1}{2}.$

Busquemos puntos fijos:

\begin{align*}
&f(x)&=x \\
\iff &\frac{x}{2}+6 &=x \\
\iff &6 &\, = \frac{x}{2} \\
\iff &12 & = x
\end{align*}

Entonces $12$ es el único punto fijo de $f.$

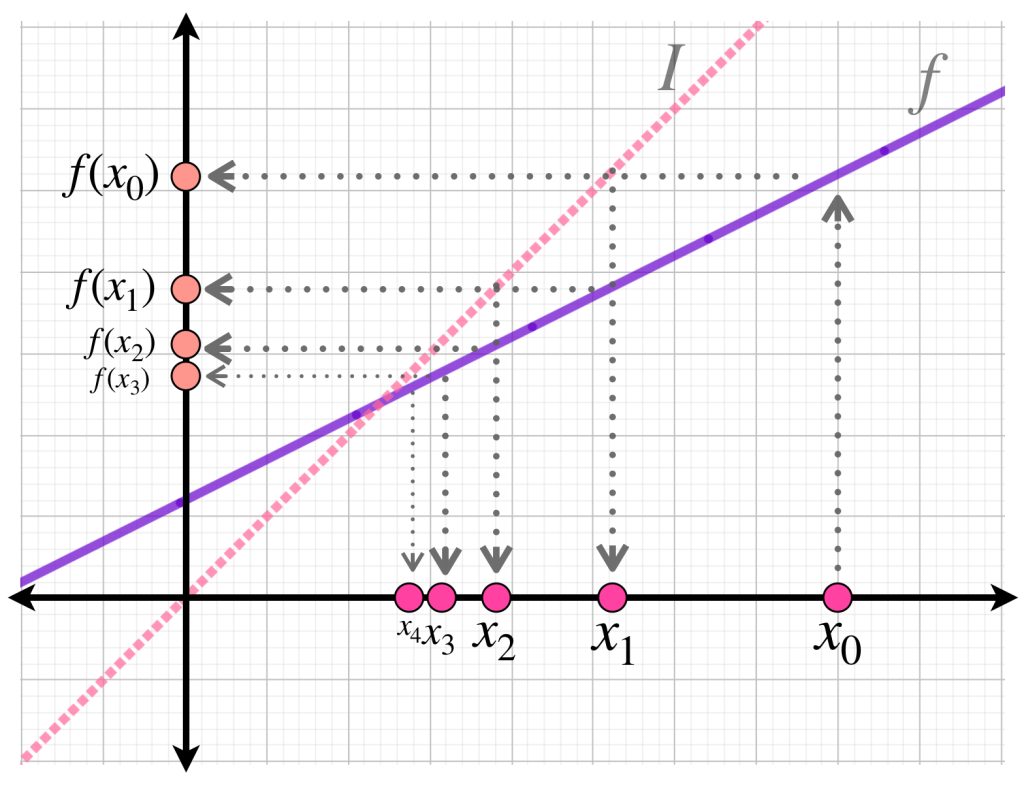
El siguiente gráfico nos confirma estos resultados para la sucesión generada a partir de un punto $x_0 \in X$ donde para cada $n \in \mathbb{N}, \, x_n=f(x_{n-1}).$

Queda como ejercicio al lector demostrar que $(x_n)_{n \in \mathbb{N}} \to 12$ en $\mathbb{R}.$

Esto da pie para enunciar el:

Teorema de punto fijo de Banach. Sea $(X,d)$ un espacio métrico completo y sea $\phi:X \to X$ una contracción, entonces:

1. Para cada $x_0 \in X$ la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy y, en consecuencia $(\phi^n(x_0))_{n \in \mathbb{N}}$ converge a un punto $x^* \in X.$ $\, \phi^n$ representa la composición $\, \underset{n \, veces}{\underbrace{ \phi \circ … \circ \phi }}$
2. El punto $x^*$ descrito es punto fijo de $\phi.$
3. El punto fijo es único.
4. Podemos estimar la distancia de $\phi ^n(x_0)$ a $x^*$ usando la desigualdad:
   $$d( \phi ^n(x_0),x^*) \leq \frac{\alpha^n}{1-\alpha} \, d( x_0, \phi (x_0)).$$

Por lo pronto demostremos que si una contracción tiene un punto fijo entonces este es único.

Sean $x, y \in X$ tales que $\phi(x)=x \,$ y $\, \phi(y)=y.$ Como $\phi$ es una contracción se tiene que:

$$d(x,y) = d(\phi(x),\phi(y)) \leq \alpha d(x,y) $$

Como $\alpha <1$ se sigue que:
$$\alpha d(x,y) \leq d(x,y)$$
Por lo tanto $d(x,y)=d(x,y),$ y en consecuencia $x=y.$

Más adelante…

Continuaremos con la demostración del teorema de punto fijo de Banach. En la siguiente entrada comprobaremos que la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy.

Tarea moral

1. Sea $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) = \dfrac{x}{2} +6$ en el espacio euclidiano. Sea $x_0 \in \mathbb{R}, \,$ prueba que la sucesión $(f^n(x_0))_{n \in \mathbb{N}} \, $ converge a $12.$
2. Sea $f:[a,b] \to [a,b], \, a,b \in \mathbb{R} \,$ una función continua. Demuestra que tiene al menos un punto fijo.
3. Da un ejemplo de una función continua $f:[a,b] \to [a,b], \, a,b \in \mathbb{R} \,$ con una infinidad de puntos fijos.
4. Prueba que si $f: \mathbb{R} \to \mathbb{R}$ y para cada $x \in \mathbb{R}, \, |f'(x)| \leq M<1$ entonces $f$ es una contracción.
5. Da un ejemplo de un espacio métrico completo y una función $\phi: X \to X \,$ que satisface que para todo $x \neq y \in X, \, d(\phi(x), \phi(y)) < d(x,y)$ pero que no tenga ningún punto fijo.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.