$ \textit{ MATERIAL EN REVISIÓN}$

Introducción

«En el Análisis tropezamos, casi siempre, con espacios provistos tanto de una topología como de operaciones de adición de elementos y multiplicación de éstos por números, es decir, tropezamos con los así llamados espacios topológicos lineales. Entre estos espacios, constituyen una clase importante los espacios normados. La teoría fue desarrollada en los trabajos de S. Banach y de otros autores». (Kolmogorov,1975).

Probablemente recuerdes de tus cursos de Geometría Analítica y Álgebra Lineal, el concepto de espacio vectorial (puedes revisarlo en Álgebra Lineal I: Espacios vectoriales). En esta entrada retomaremos la noción que representa la «medida» de cada vector para asociar ese valor a una distancia.

Definición. Norma. Sea $V$ un espacio vectorial sobre $\mathbb R$. Se dice que una aplicación $\| \cdot \| : V \rightarrow \mathbb R$ es una norma si para todo $x,y \in V$ y para todo $\lambda \in \mathbb R$ se satisface:

1. $\| x \|=0 \iff x=0$
2. $\|\lambda x\| = |\lambda| \|x\|$
3. $\|x + y\| \leq \|x\|+\|y\|$

El espacio vectorial $(V,\|\cdot\|)$ es llamado espacio normado.

A continuación ilustramos dichos axiomas en el espacio vectorial $\mathbb{R}^2,$ donde los vectores suelen representarse con flechas que inician en el origen y terminan en el punto del plano a representar.

Usaremos la norma euclidiana, donde para $(x,y) \in \mathbb{R}^2$
$$\|(x,y)\| := \sqrt{x^2 + y^2}.$$

Nota que la norma de un vector $\vec{u} = (x,y) \in \mathbb{R}^2$ equivale a la distancia euclidiana que hay entre el origen y el punto $(x,y).$

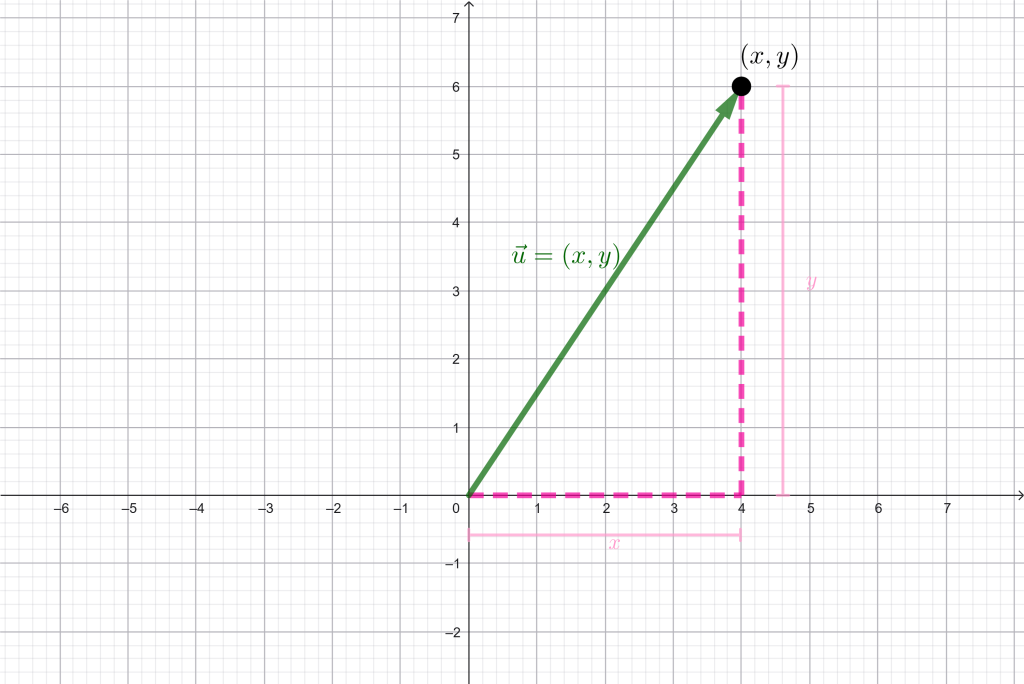
De acuerdo con el primer axioma, la norma de un vector es cero si y solo si, el vector es cero. En este caso, el vector cero es $(0,0).$

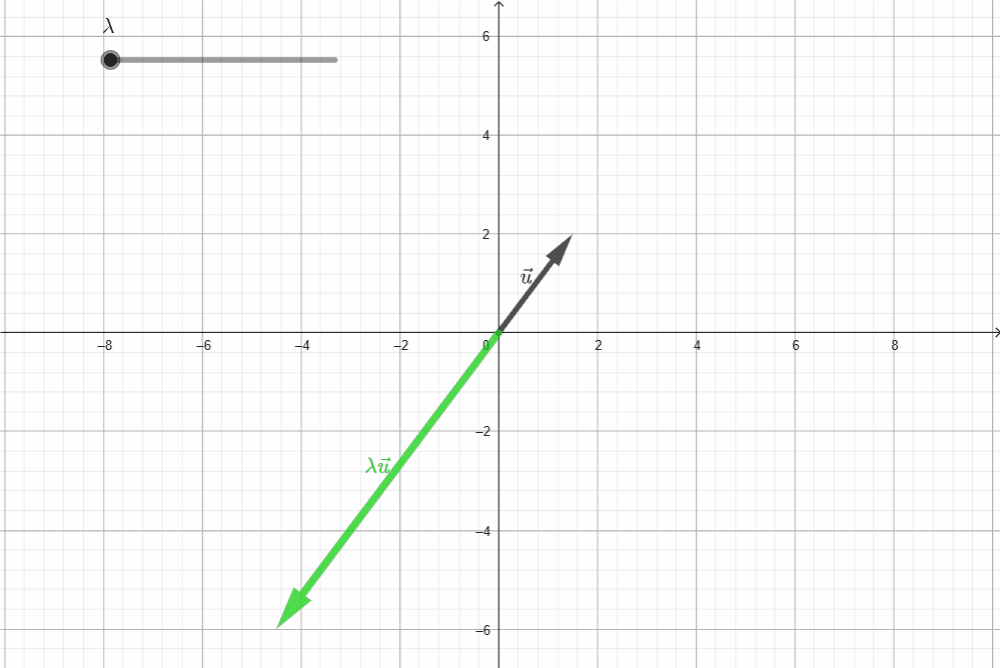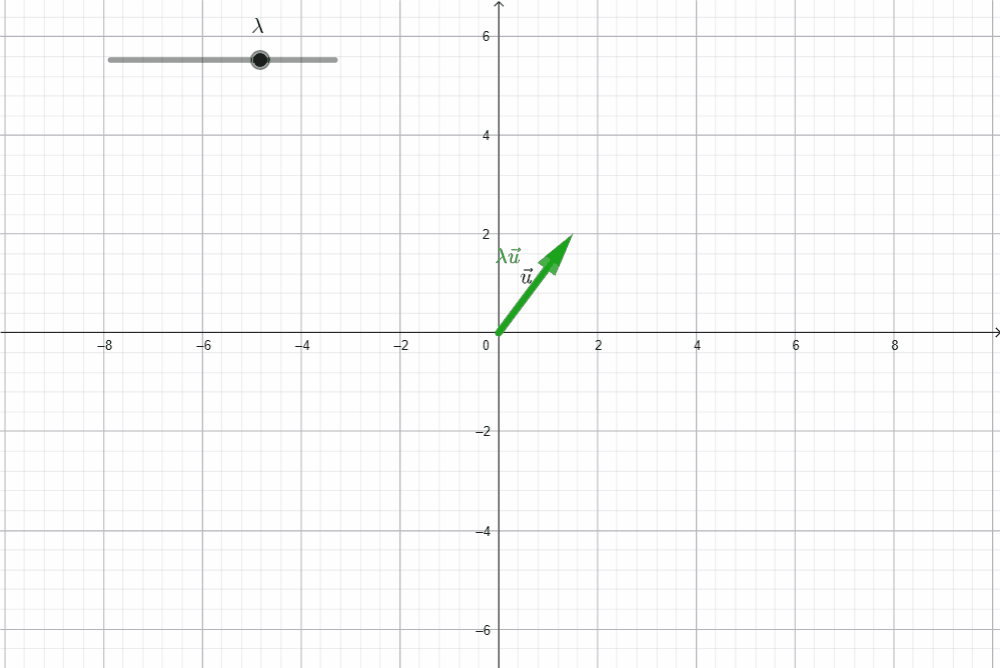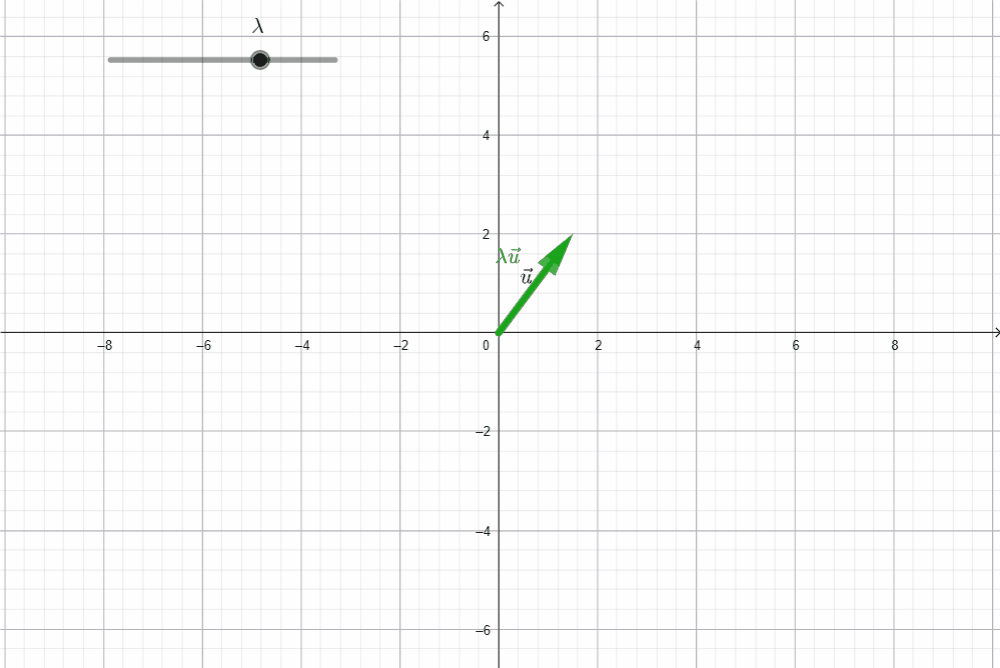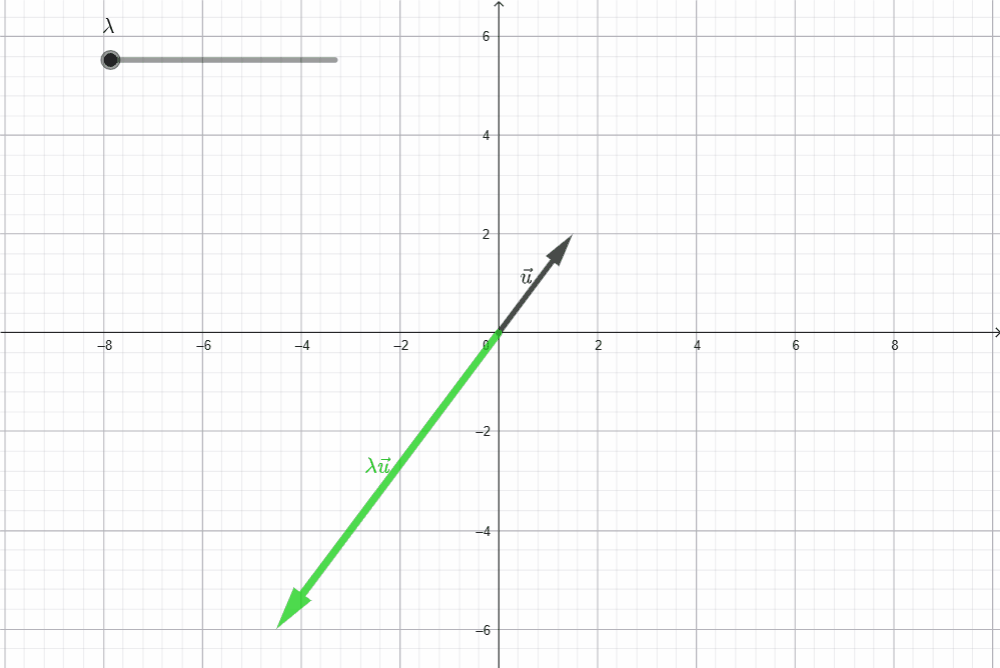
El segundo axioma habla del producto de un vector por un escalar. Sea $\vec{u}$ un vector en $\mathbb{R}^2,$ la igualdad $\|\lambda \vec{u}\| = |\lambda| \|\vec{u}\|$ indica que el tamaño de la flecha de $\vec{u}$ cambia en proporción con el valor de $\lambda.$ En el siguiente gráfico, el vector en verde, muestra a $\, \vec{u} \,$ luego de ser multiplicado por un escalar en el intervalo $(-3,3).$

El tercer axioma dice que la norma de la suma de dos vectores es menor igual que la suma de la norma de cada uno. La siguiente imagen visualiza que, si $\vec{u}$ y $\vec{w}$ son vectores en $\mathbb{R}^2,$ la magnitud de la flecha que representa $\vec{u}+\vec{w}$ es menor igual que la suma de las magnitudes de las flechas de $\vec{u}$ y $\vec{w}.$ Esta propiedad, en el caso de las normas, también se conoce como desigualdad del triángulo.

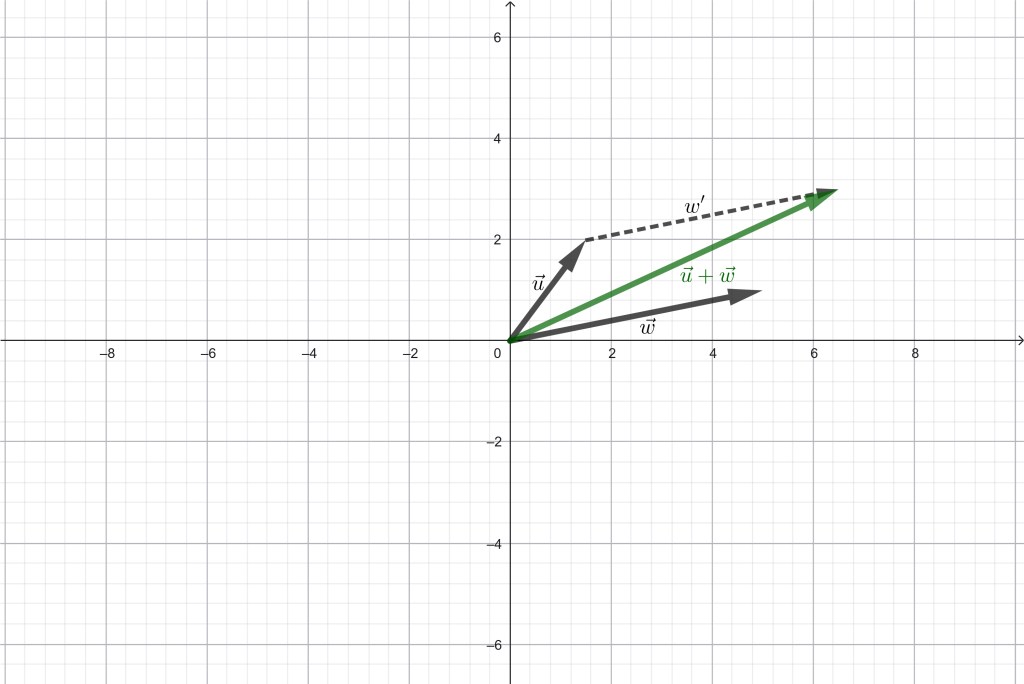
Ahora veremos que un espacio normado $V$ es también un espacio métrico, si para dos puntos $x,y \, \in V \,$se define la distancia como:

$$d(x,y):=\|x-y\|$$

Probemos que $d$ es una métrica.

Demostración: Sean $x,y,z \in V$

1. $d(x,x)=\|x-x\|=\|0\|\iff x=0$
2. $d(x,y)=\|x-y\|=\|(-1)(-x+y)\|=|-1|\|-x+y\|=1\|y-x\|=\|y-x\|=d(y,x)$
3. $d(x,y)=\|x-y\|=\|x-z+z-y\|\leq \|x-z\|+\|z-y\|=d(x,z)+d(z,y).$

Ya que sabemos que un espacio normado induce un espacio métrico, notemos que el recíproco no siempre es válido, es decir:

Proposición. No todos los espacios métricos son inducidos por espacios normados.

Demostración: Considera $X \subset \mathbb{R} \,$ tal que $\, X \neq \{0\} \,$ con $\, d \,$ la métrica discreta definida en Espacios métricos, entonces si tomamos $x\in \mathbb{R} \,$ con $\, x \neq 0$ y suponemos que existe una norma para este espacio, se tienen que cumplir las siguientes igualdades:
$\|2x\|=|2|\|x\|=|2|\|x-0\|=|2|d(x,0)=2(1)=2$
Lo cual no puede ser, pues la distancia únicamente asigna valores en $\{0,1\}.$

Ejemplos de normas en espacios vectoriales:

1. La norma $\mathbf{p.}$
   Sea $\, p \,$ $\in [1, \infty)$ y $x \in \mathbb {R}^n$. Si $x=(x_1,…, x_n)$, definimos:
   $\| x \|_p := (\sum_{i=1}^n |x_i|^p ) ^ {1/p}.$
2. La norma infinito en $\mathbf{\mathbb {R}^n}.$
   Sea $x \in \mathbb {R}^n.$ Definimos:
   $\|x\|_\infty := max \{|x_1|,…,|x_n|\}.$
3. La norma infinito en el espacio de funciones reales continuas en el intervalo $\mathbf{[a,b].}$
   En el espacio vectorial $C^0[a,b],$ para $f \in C^0[a,b]$ definimos:
   $\norm{f}_\infty :=\underset{a \leq t \leq b}{max} \, |f(t)|.$
4. La norma infinito en el conjunto de sucesiones reales acotadas.
   Sea $\ell_\infty$ el conjunto de sucesiones acotadas de números reales. Si $(x_{n})_{n \in \mathbb{N}} \in \ell_\infty,$ definimos:
   $\norm{(x_{n})_{n \in \mathbb{N}}}_\infty :=\underset{n \in \mathbb{N}}{sup} \, |x_{n}|.$

Más adelante…

Ya que reconocemos la distancia entre dos puntos procederemos a identificar todos los puntos que están «cerca» de un punto específico. ¿Te suena familiar? Vamos a ver si el conjunto formado por estos puntos es diferente al que estamos acostumbrados a representar como una bola redonda de radio $\epsilon > 0$.

Tarea moral

1. Demuestra que si $(V,\|\cdot \|)$ es un espacio normado, entonces $\forall \, x \in V, \norm{x} \geq 0$.
2. Demuestra que la norma $p$ con $p=2,$ es decir, $\| x \|_2$ induce la métrica euclidiana.
3. Demuestra que la norma del ejemplo $3$ induce la métrica en el espacio de funciones continuas vista en Espacios métricos.
4. Demuestra que en el conjunto de números complejos $\mathbb{C}$ pueden definirse las normas de los ejemplos $1$ y $2.$

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 57-59.
• Bartle, R.G., The Elements of Real Analysis. New York: J. Wiley, 1964. Págs: 59-64.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 11-21.
• Jost, J., Postmodern Analysis (3rd ed.). New York: Springer-Verlag, 2005. Págs: 44,45.
• Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 149-151.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.