$\textit{MATERIAL EN REVISIÓN}$
Introducción
Para probar el teorema de Arzelá-Ascoli que veremos más adelante, usaremos familias de funciones que tienen la propiedad de enviar puntos muy cercanos del dominio a puntos muy cercanos en el contradominio. Suena a funciones continuas, ¿verdad? No obstante, en esta ocasión será el mismo valor de delta el que haga válida la cercanía para cualquier función.
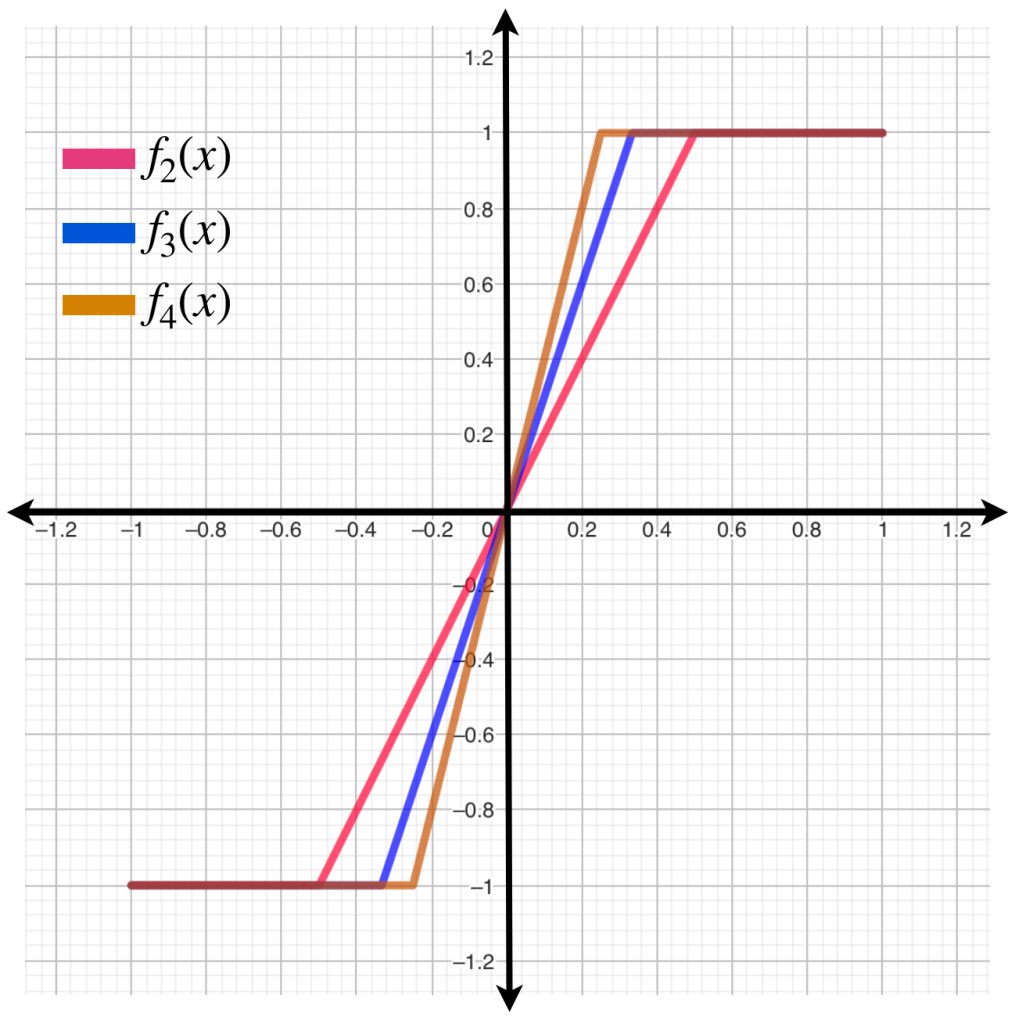
Ejemplo: Considera el conjunto de funciones $\{f_k \, | \, f_k \in \mathcal{C}^0[-1,1], \, k \in \mathbb{N}\}, \,$ donde
\begin{equation*}
f_k(x) := \begin{cases}
-1 \, &\text{ si $x \in [-1, – \frac{1}{k}]$},\\
kx \, &\text{ si $x \in [-\frac{1}{k}, \frac{1}{k}]$}, \\
1 \, &\text{ si $x \in [\frac{1}{k},1]$}.
\end{cases}
\end{equation*}
Estas funciones son continuas en $\mathbb{R}$, más aún, son uniformemente continuas en $\mathbb{R}.$ Sea $\varepsilon >0.$ Cada una de las funciones tiene una $\delta>0$ que hace que puntos a distancia menor que esa delta sean enviados, bajo la función, a puntos de distancia menor que $\varepsilon.$ ¿Será posible encontrar un valor de $\delta$ que cumpla la propiedad para cualquier función $f_k$?
No, no es así. Dejaremos como ejercicio demostrar que para cada $\delta >0$ (y menor que $1$) existe una función $f_k$ tal que $|f_k(0) \, – \, f_k(\frac{\delta}{2})|> \varepsilon = \frac{1}{2}$ de modo que no es posible encontrar un valor de $\delta$ que funcione para todas las funciones del conjunto.
La propiedad que estamos describiendo se conoce como equicontinuidad. Presentamos la definición de:
Simon, B., Real Analysis A Comprehensive Course in Analysis, Part 1,. USA: American Mathematical Society, 2015, pág 70.
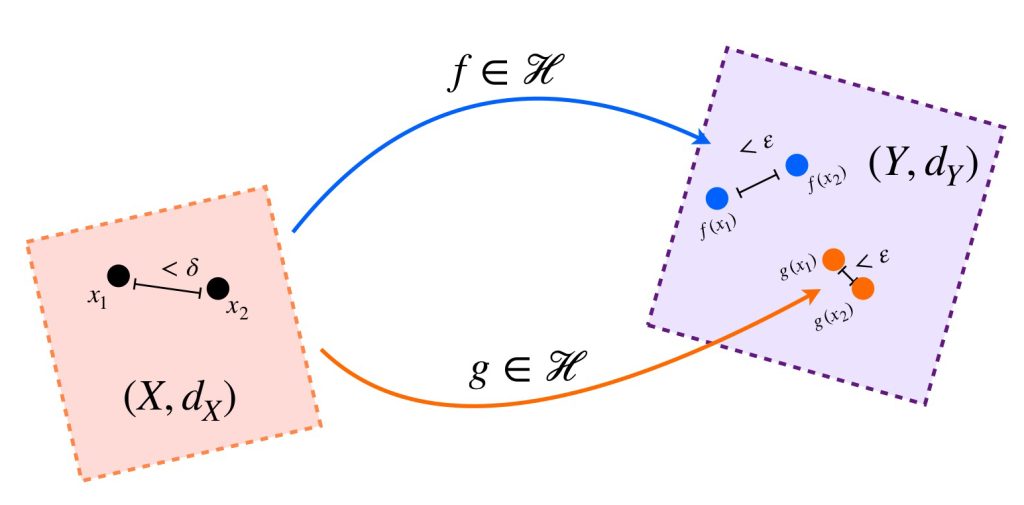
Definición. Familia uniformemente equicontinua. Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos y $\mathcal{H} \,$ una familia de funciones de $X$ en $Y.$ Diremos que $\mathcal{H} \,$ es uniformemente equicontinua si para cada $\varepsilon >0$ existe $\delta >0$ tales que para cualesquiera $x_1, x_2 \in X$ que cumplen que $d_X(x_1,x_2)< \delta\, $ entonces para cualquier $f \in \mathcal{H}, \,$ $d_Y(f(x_1),f(x_2)) < \varepsilon.$
En particular, si $Y$ es el espacio de los complejos con la métrica euclidiana tenemos la definición de:
Rudin, W., Principios de Análisis Matemático (3a ed.). México: McGraw–Hill, 1980, pág 156.
Definición. Familia equicontinua de funciones complejas. Sea $\mathcal{H}$ una familia de funciones complejas con dominio en un espacio métrico $(X,d_X).$ Diremos que $\mathcal{H} \,$ es equicontinua en $X$ si para cada $\varepsilon >0$ existe $\delta >0$ tales que para cualesquiera $x_1, x_2 \in X$ que cumplen que $d_X(x_1,x_2)< \delta\, $ entonces para cualquier $f \in \mathcal{H}, \,$ $\norm{f(x_1) \, – \, f(x_2)} < \varepsilon.$
Nota que toda función de una familia equicontinua es uniformemente continua.
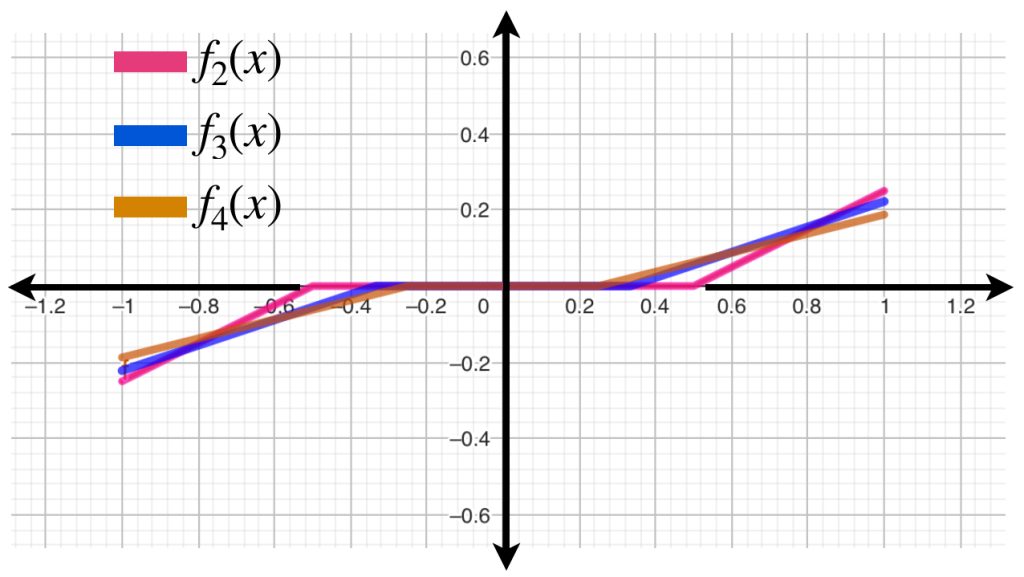
Ejemplo: Ahora tomemos una sucesión de funciones en $\mathcal{C}^0[-1,1]\,$ donde para cada $k \in \mathbb{N} \,$ la función $f_k \,$ se define como
\begin{equation*}
f_k(x) := \begin{cases}
\frac{1}{k}(x+\frac{1}{k}) \, &\text{ si $x \in [-1, – \frac{1}{k}]$},\\
0 \, &\text{ si $x \in [-\frac{1}{k}, \frac{1}{k}]$}, \\
\frac{1}{k}(x-\frac{1}{k}) \, &\text{ si $x \in [\frac{1}{k},1]$}.
\end{cases}
\end{equation*}
Dejaremos como ejercicio probar que la sucesión converge uniformemente a la función constante cero y que la familia $\{f_k\}_{k \in \mathbb{N}} \,$ es uniformemente equicontinua.
Las condiciones de esta sucesión se generalizan según expresa la siguiente:
Proposición. Sea $(X,d_X)$ un espacio métrico compacto y $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones en $\mathcal{C}^0(X, \mathbb{C})$ (continuas) tal que la sucesión converge uniformemente en $X.$ Entonces $\{ f_n \} _{n \in \mathbb{N} \,}$ (el conjunto de las funciones de la sucesión) es uniformemente equicontinua sobre $X.$
Demostración:
Sea $\varepsilon >0.$ Como la sucesión de funciones $(f_n)_{n \in \mathbb{N}}\,$ converge uniformemente en $X,$ de acuerdo con la entrada Convergencia puntual y convergencia uniforme, como $\mathbb{C}$ es completo, $(f_n)_{n \in \mathbb{N}}\,$ es uniformemente de Cauchy, por lo tanto existe $N \in \mathbb{N}$ tal que para cada $n \geq N$ se cumple que
\begin{align}
\norm{f_n \, – \, f_N} _\infty < \frac{\varepsilon}{3}.
\end{align}
En la entrada Continuidad uniforme vimos que cada función continua con dominio compacto es uniformemente continua. En particular, para cada una de las primeras funciones de la sucesión, $f_1, \, f_2, …, f_N,$ existe su correspondiente $\delta_i, \, i=1,…,N$ tal que para cada $i = 1,…,N, \,$ siempre que $d_X(x_1,x_2) < \delta_i,$ tenemos:
\begin{align}
\norm{f_i(x_1) \, – \, f_i(x_2)} < \frac{\varepsilon}{3}.
\end{align}
Si hacemos
$$\delta < \text{min} \{d_i \, | \, i=1,…,N\}$$
se sigue cumpliendo (2) para $i = 1,…,N$
mientras que si $n>N$ se concluye de la desigualdad del triángulo, de (1) y de (2) que
\begin{align*}
\norm{f_n(x_1) \, – \, f_n(x_2)} &\leq \norm{f_n(x_1) \, – \, f_N(x_1)} + \norm{f_N(x_1) \, – \, f_N(x_2)} + \norm{f_N(x_2) \, – \, f_n(x_2)} \\
&< \frac{\varepsilon}{3}+ \frac{\varepsilon}{3} + \frac{\varepsilon}{3} \\
&= \varepsilon.
\end{align*}
Por lo tanto el conjunto de funciones en $(f_n)_{n \in \mathbb{N}} \,$ es equicontinuo.
La definición a considerar en el teorema de Arzelá-Ascoli
En la sección Teorema de Arzelá-Ascoli nuestra familia de funciones tendrá un dominio compacto y consideraremos la definición de equicontinuidad que aparece en
Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2015, pág 125.
Nota que la propiedad se fija en un punto:
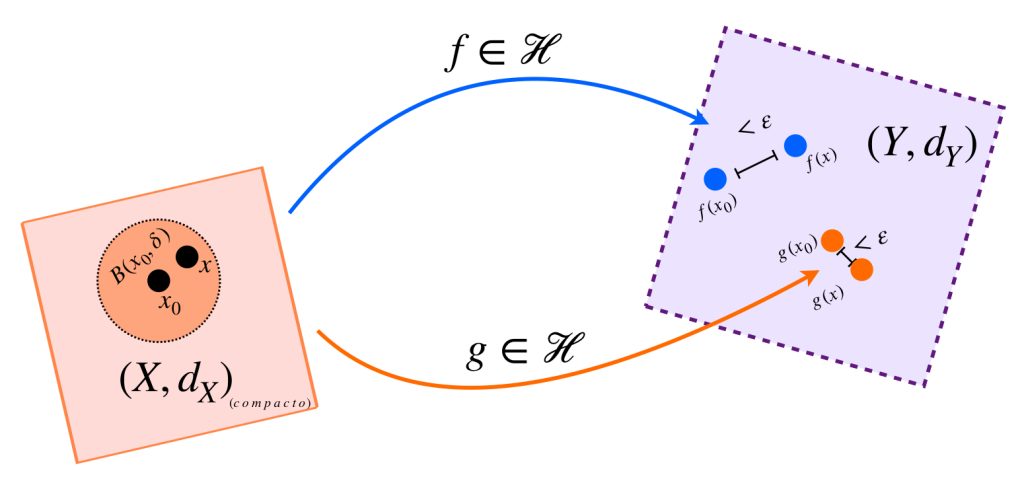
Definición. Familia equicontinua en un punto. Sea $(X,d_X)$ un espacio métrico compacto y $(Y,d_Y)$ un espacio métrico. Sea $\mathcal{H} \subset \mathcal{C^0}(X,Y)$ es decir, $\mathcal{H}$ es una familia de funciones continuas con dominio en $X$ e imagen en $Y.$ Diremos que $\mathcal{H}$ es equicontinuo en el punto $x_0 \in X$ si para todo $\varepsilon>0,$ existe $\delta>0$ tal que para toda función $f$ en $\mathcal{H}$ se cumple que si $d_X(x,x_0)<\delta$ entonces $d_Y(f(x),f(x_0))<\varepsilon.$
Esta definición se relaciona con la primera en el siguiente sentido:
Proposición. Si $\mathcal{H}$ es uniformemente equicontinua entonces es equicontinua en cada punto de $X.$
Demostración:
Sea $x_0 \in X$ y $\varepsilon > 0. \,$ Como $\mathcal{H}$ es uniformemente equicontinua, existe $\delta >0$ tal que para cada $x_1, x_2 \in X$ si $d_X(x_1,x_2)< \delta$ entonces $d_Y(f(x_1),f(x_2))< \varepsilon$ para cualquier $f \in \mathcal{H}.$ En particular para cada $x \in X,$ si $d_X(x,x_0)< \delta$ entonces $d_Y(f(x),f(x_0))< \varepsilon$ para cualquier $f \in \mathcal{H} \,$ lo cual prueba que la familia de funciones es equicontinua en $x_0.$
La última definición pide que el dominio de las funciones sea compacto. Esto permite elegir una delta que funcione para todos los elementos de $\mathcal{H}.$
Proposición: Si $\mathcal{H}$ es es equicontinua en cada punto de $X,$ como en la definición entonces es uniformemente equicontinua.
Demostración: Se dejará como ejercicio.
El recíproco no es cierto si quitamos la compacidad de $X$. Ser equicontinua puntualmente no implica ser uniformemente equicontinua. Se te pedirá un contraejemplo.
Más adelante…
Usaremos las nociones aprendidas recientemente para conocer y probar el teorema de Arzelá-Ascoli.
Tarea moral
- Resuelve los dos ejemplos de esta sección.
- Prueba que si $\mathcal{H}$ es es equicontinua en cada punto de $X,$ como en la definición (con $X$ compacto) entonces es uniformemente equicontinua.
- Muestra un ejemplo de una familia equicontinua puntualmente en todos los puntos del dominio pero que no sea uniformemente equicontinua.
Bibliografía
- Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2015. Págs: 125 y 126.
- Rudin, W., Principios de Análisis Matemático (3a ed.). México: McGraw–Hill, 1980, pág 156-158.
- Simon, B., Real Analysis A Comprehensive Course in Analysis, Part 1,. USA: American Mathematical Society, 2015, pág 70.