Introducción
En entradas anteriores trabajamos ideas de convergencia de sucesiones. En ellas se observa una secuencia de puntos de un espacio métrico y se analiza si se pueden acercar mucho entre ellos o si se acercan a algún otro punto. En esta entrada, y otras correspondientes a la sección, observaremos sucesiones originadas por puntos obtenidos al evaluar funciones. Al comparar distancias entre puntos de la imagen de esas funciones podemos pensar ahora en cercanía de funciones, más aún, en si se aproximan a alguna función específica. ¡Comenzamos!
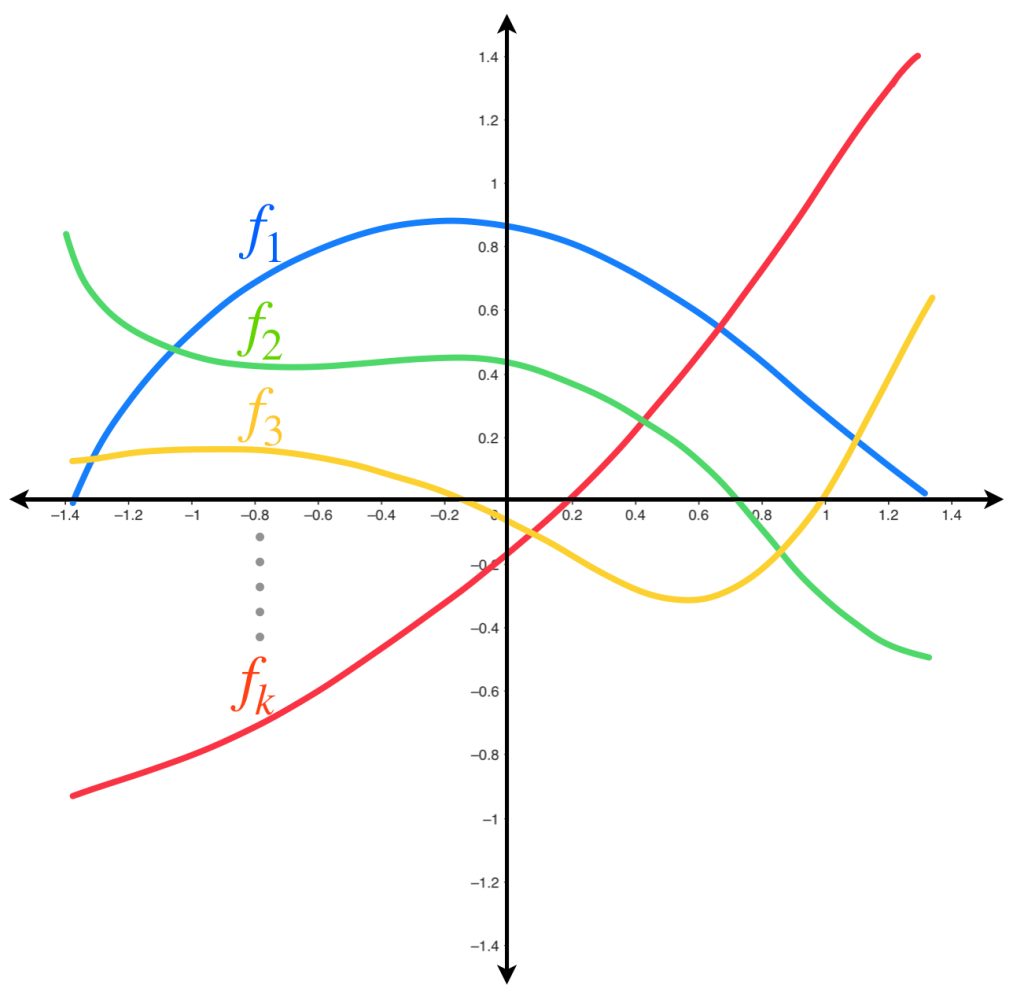
Sea $A$ un conjunto y $(X,d)$ un espacio métrico. Para cada $n \in \mathbb{N}$ considera una función $f_n:A \to X.$ Esto define una sucesión de funciones $(f_n)_{n \in \mathbb{N}}.$
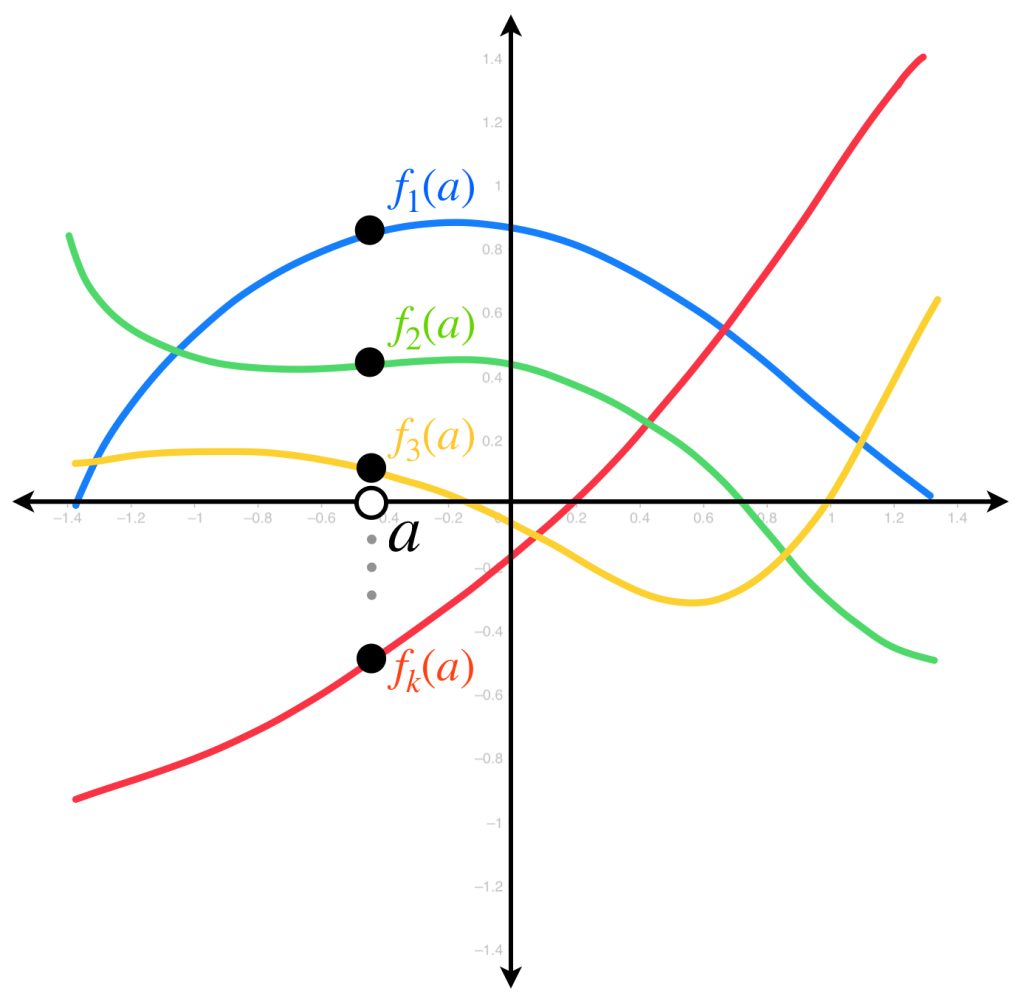
A partir de un punto $a \in A$ (fijo) podemos definir otra sucesión con los valores que cada una de las funciones anteriores asignan a ese punto. Es decir, con los términos $f_1(a), f_2(a), f_3(a), …$ definimos la sucesión $(f_n(a))_{n \in \mathbb{N}}.$
Es natural preguntarse si esa sucesión de puntos es convergente. Gráficamente podemos observar que esto depende de cómo están definidas las funciones y también del valor $a$ elegido en el dominio $A.$ Por ejemplo, en el siguiente dibujo, la sucesión generada con las funciones evaluadas en $a_1$ es convergente, pues los puntos se van aproximando al eje horizontal. Por otro lado, la generada a partir del punto $a_2$ no lo es; sus puntos tienden a infinito.
Para formalizar estas ideas, al final de esta sección se te pedirá demostrar que la sucesión de funciones del ejemplo anterior evaluadas en $a_1$ (un punto menor que cero), es convergente. ¿Cuál es el límite? Por el contrario, para un punto mayor que cero la sucesión tiende a infinito. ¿Qué pasa al evaluar las funciones en cero?
Pero en un conjunto donde todos los puntos $a$ forman sucesiones convergentes $(f_n(a))_{n \in \mathbb{N}},$ podemos pensar en cada límite de esas sucesiones como el valor que otra función $f$ asigna en cada punto $a.$ Eso inspira la siguiente:
Definición. Convergencia puntual: Si $(f_n)_{n \in \mathbb{N}} \,$ es una sucesión de funciones donde para cada $n \in \mathbb{N}$ se tiene $f_n: A \to X,$ decimos que $(f_n)_{n \in \mathbb{N}} \,$ converge puntualmente en $A$ a una función $f:A \to X$ si para cada punto $a \in A$ se cumple que $\underset {n \to \infty}{lim} \, f_n(a) = f(a).$
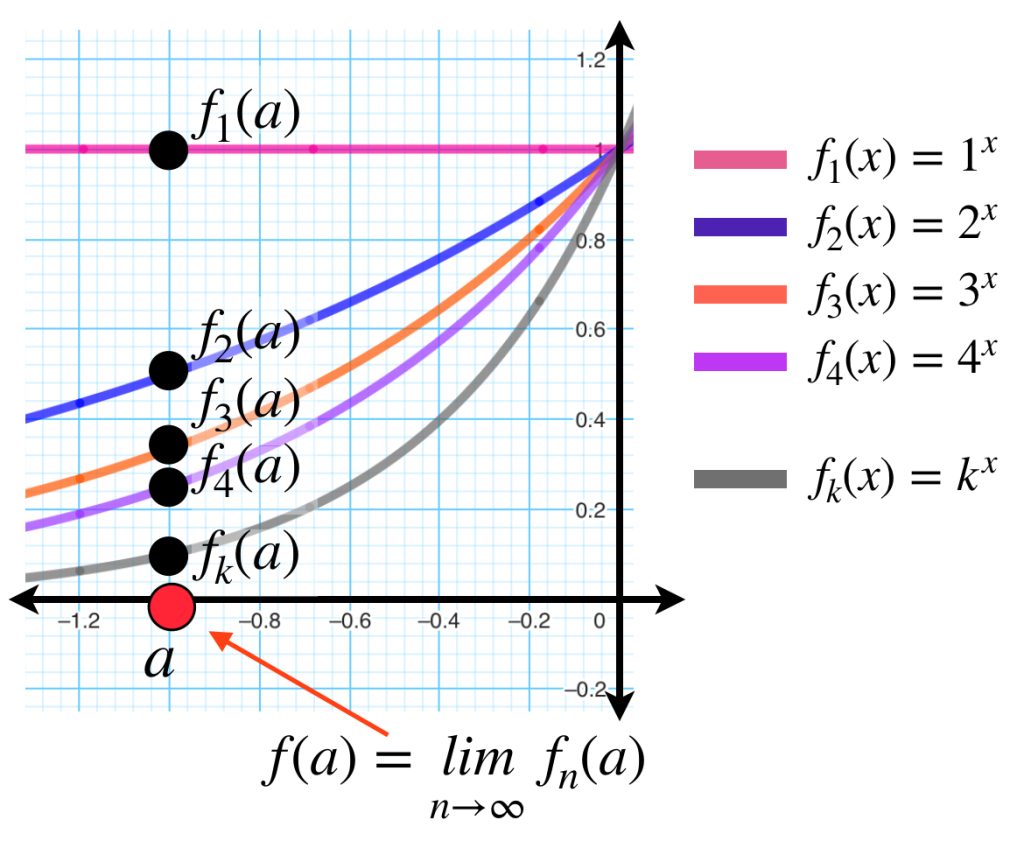
Aunque la sucesión de funciones del ejemplo anterior no converge puntualmente en $\mathbb{R},$ sí lo hace en el intervalo $(- \infty , 0].$ Converge puntualmente a la función dada por:
\begin{equation*}
f(x) = \begin{cases}
0 & \text{si $x < 0$} \\
1 & \text{si $x = 0$}
\end{cases}
\end{equation*}
La función $f$ recibe el nombre de límite puntual de la sucesión de funciones $(f_n)_{n \in \mathbb{N}}.$
De acuerdo con la definición de convergencia puntual, para cada $\varepsilon >0$ y cada $a \in A$ se requiere de la existencia de un número $N_a \in \mathbb{N}$ tal que $\forall \, n\geq N_a, \, d(f_n(a),f(a)) < \varepsilon.$
Es importante notar que, incluso cuando todas las sucesiones $(f_n(a))_{n \in \mathbb{N}} \,$ son convergentes, posiblemente el natural $N_a \,$ que satisface la definición de convergencia será diferente al variar el punto $a$ en el dominio, de ahí que lo indiquemos con un subíndice.
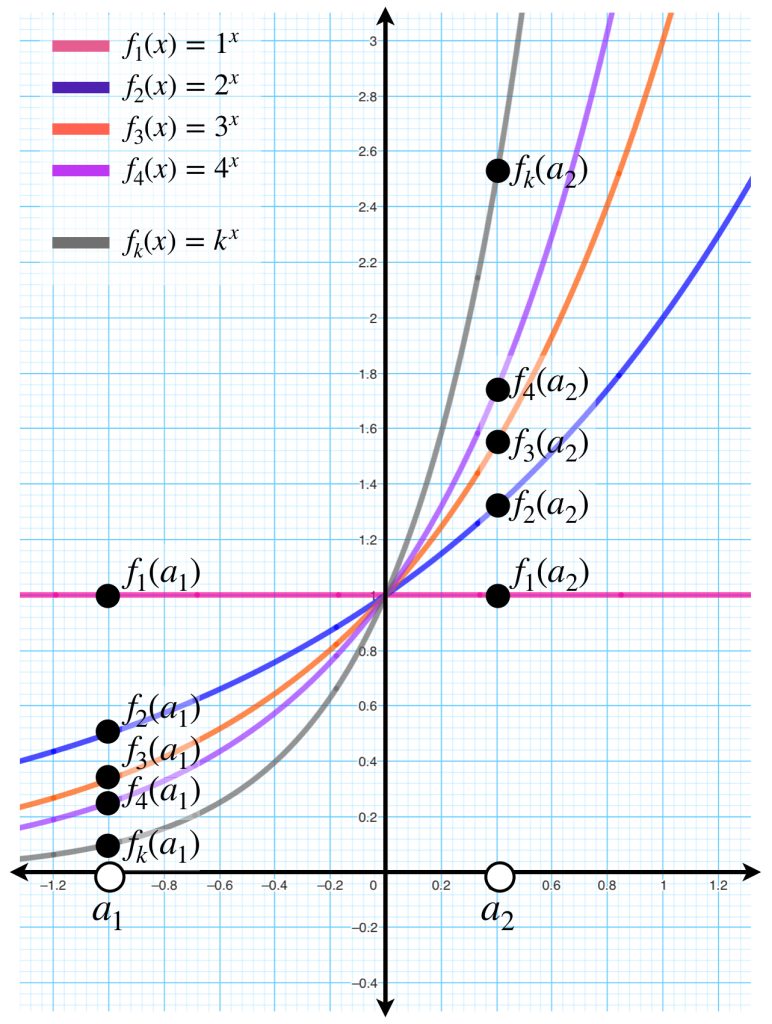
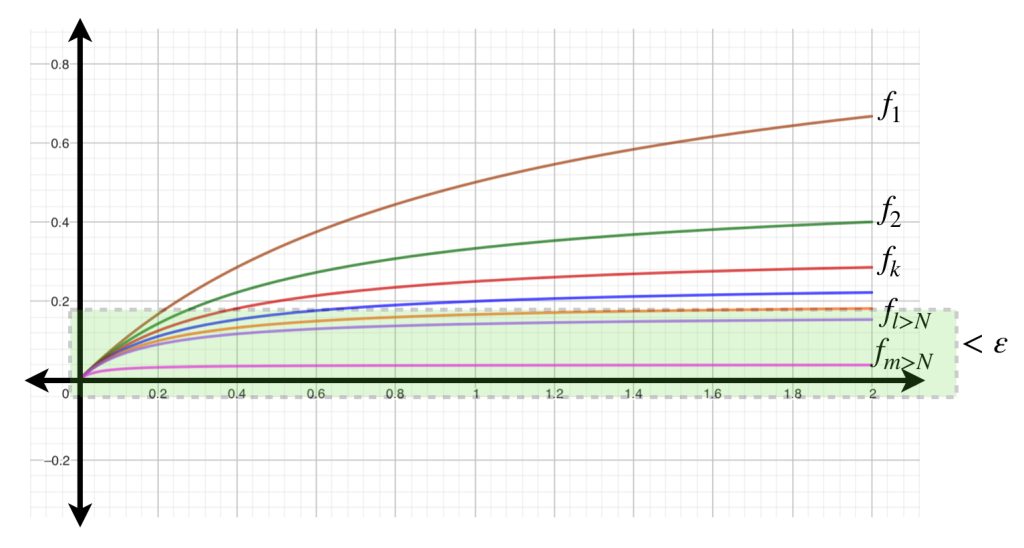
Tomemos nuevamente el ejemplo anterior en el intervalo $(- \infty, 0]$ donde la sucesión de funciones converge puntualmente. Partiendo de un $\varepsilon_0 >0$ fijo, observemos las siguientes sucesiones, en distintos valores del intervalo.
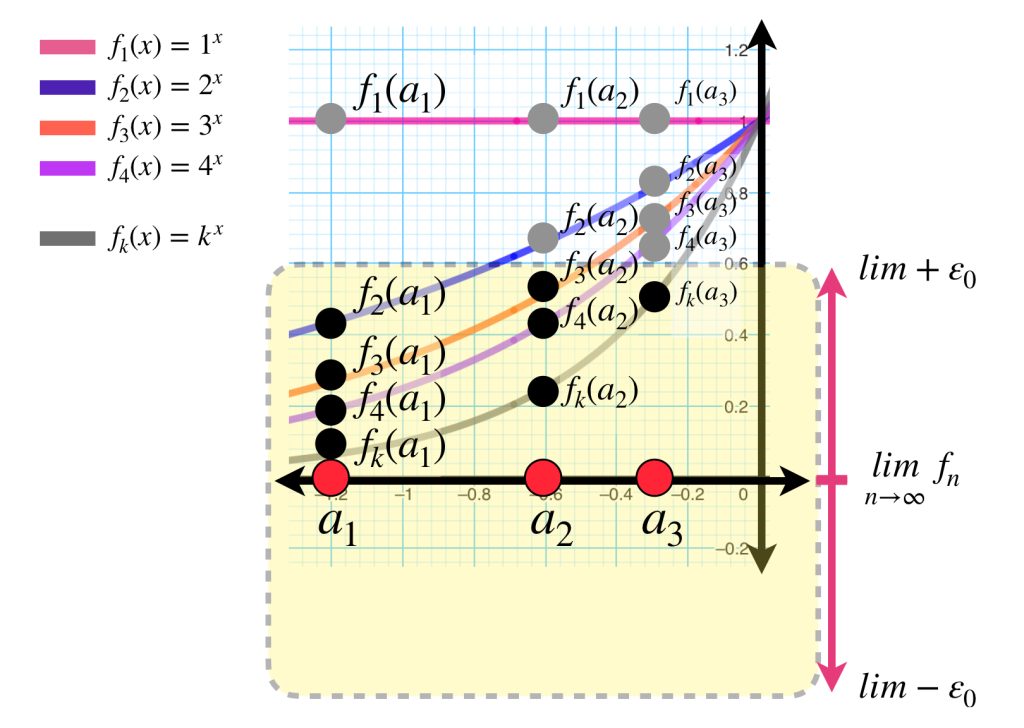
Mientras que para el punto $a_1$ la sucesión se acerca al punto de convergencia $f(a_1) = 0$ en distancias menores que $\varepsilon _0$ a partir del punto evaluado en $f_2,$ para el punto $a_2$ no se acerca lo suficiente sino hasta $f_3.$ Por otra parte, los puntos de las funciones evaluadas en $a_3$ del dibujo, no se acercan en menos que $\varepsilon _0$ a su respectivo punto de convergencia sino hasta a partir de $f_k.$ Entonces, los naturales que satisfacen la condición pueden proponerse como:
$$N_{a_1} = 2; \, N_{a_2}=3; \, N_{a_3} = k$$
¿Es posible reasignar un mismo natural a los puntos $a_1, \, a_2, \, a_3$ y satisfacer también la definición de convergencia?
¿Será posible hacerlo en todos los puntos de $(- \infty ,0]$
Cuando para todo $\varepsilon>0$ sí sea posible asegurar la existencia de un mismo valor natural $N$ que afirme la convergencia de todas las sucesiones $(f_n(a))_{a \in A} \,$ hablaremos de que la sucesión de funciones converge uniformemente:
Definición. Convergencia uniforme: Considera una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ donde para cada $n \in \mathbb{N}, \, f_n:A \to X \, $ con $A$ un conjunto y $(X,d)$ un espacio métrico. Decimos que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente a una función $f:A \to X$ si para toda $\varepsilon >0$ existe $N \in \mathbb{N}$ tal que para toda $n \geq N$ y para toda $a \in A$ se cumple que $d(f_n(a),f(a))< \varepsilon.$
En este caso nos referiremos a $f$ como el límite uniforme de $(f_n)_{n \in \mathbb{N}}.$
Ejemplo
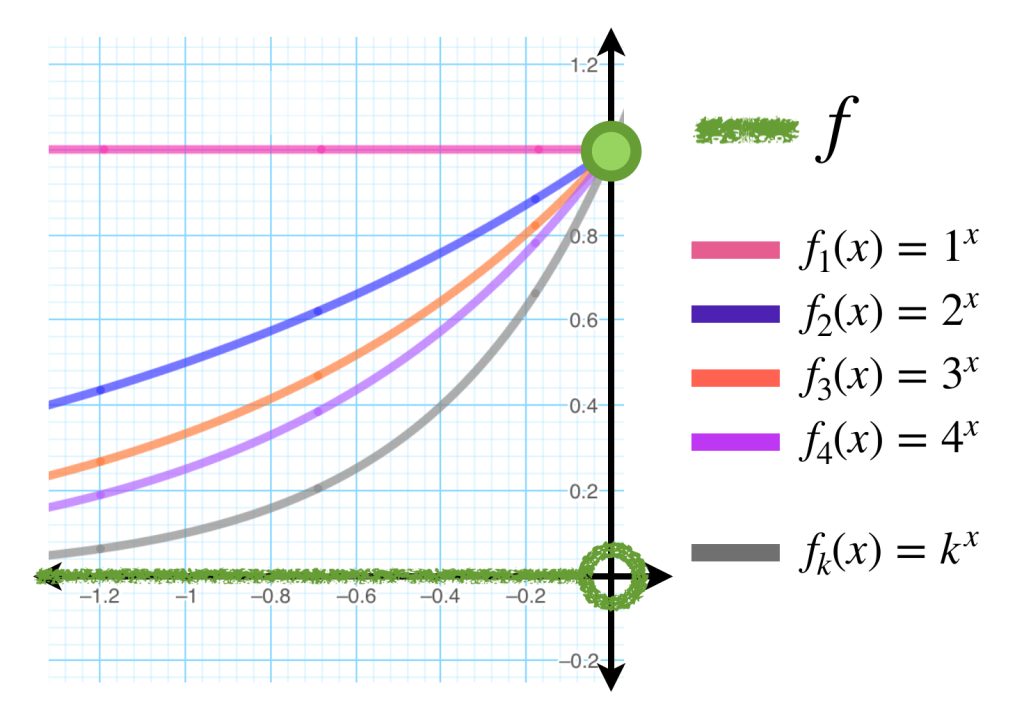
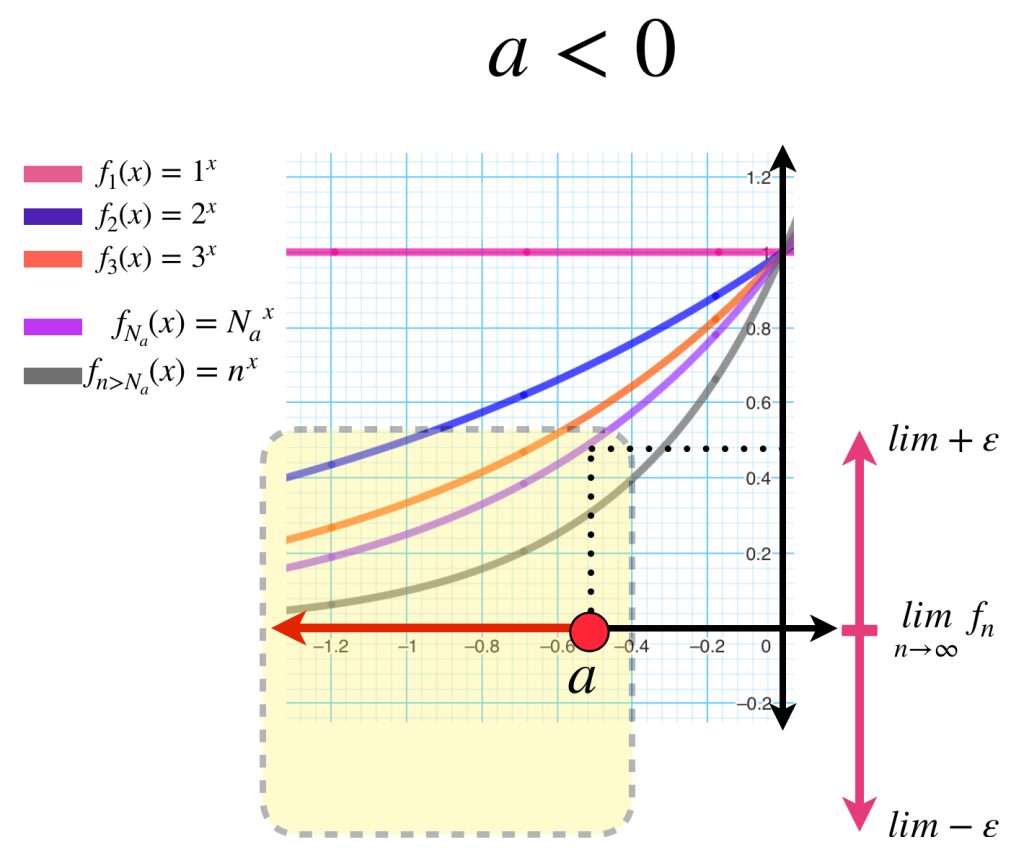
Consideremos la misma sucesión de funciones $(n^x)_{n \in \mathbb{N}} \,$ pero ahora con dominio $(- \infty, a]$ con $a < 0.$
Sea $\varepsilon >0$. Toma el $N_a \in \mathbb{N}$ que satisface que $\forall n\geq N_a, \, d(f_n(a),0) < \varepsilon$ el cual existe, pues $f_n(a) \to 0.$ Nota que este mismo natural funciona para probar la convergencia de la sucesión de puntos de funciones evaluadas en cualquier otro punto de $(- \infty,a].$ La demostración de este hecho quedará como ejercicio.
Nota que si una sucesión $(f_n)$ converge uniformemente a $f$ entonces también converge puntualmente a $f.$ Por el contrario, podemos tener sucesiones que convergen puntualmente pero no uniformemente:
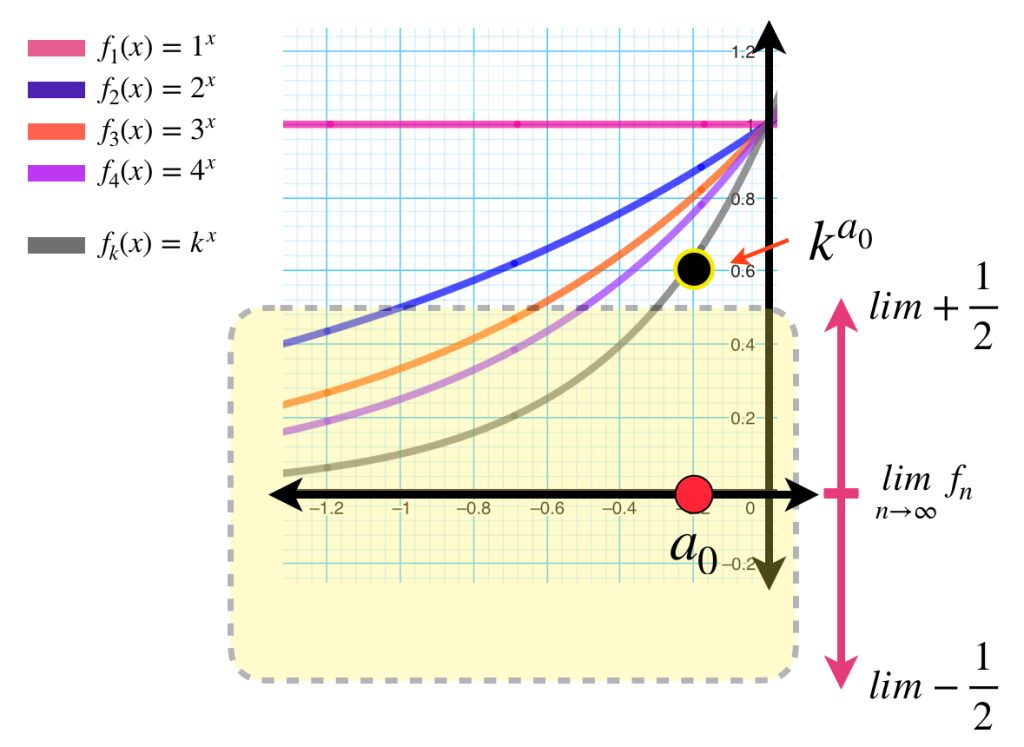
Ejemplo: Aunque la sucesión $(n^x)_{n \in \mathbb{N}} \,$ converge puntualmente en $(- \infty , 0]$ no converge uniformemente en el mismo dominio. Sea $\varepsilon = \frac{1}{2}$ y $k \in \mathbb{N}.$ Como la imagen de $k^x$ es $(0,1]$ entonces existe $a_0 \in (- \infty , 0)$ (donde $(n^{a_0})_{n \in \mathbb{N}} \to 0$) tal que $k^{a_0}> \varepsilon .$ Por lo tanto, el límite no es uniforme.
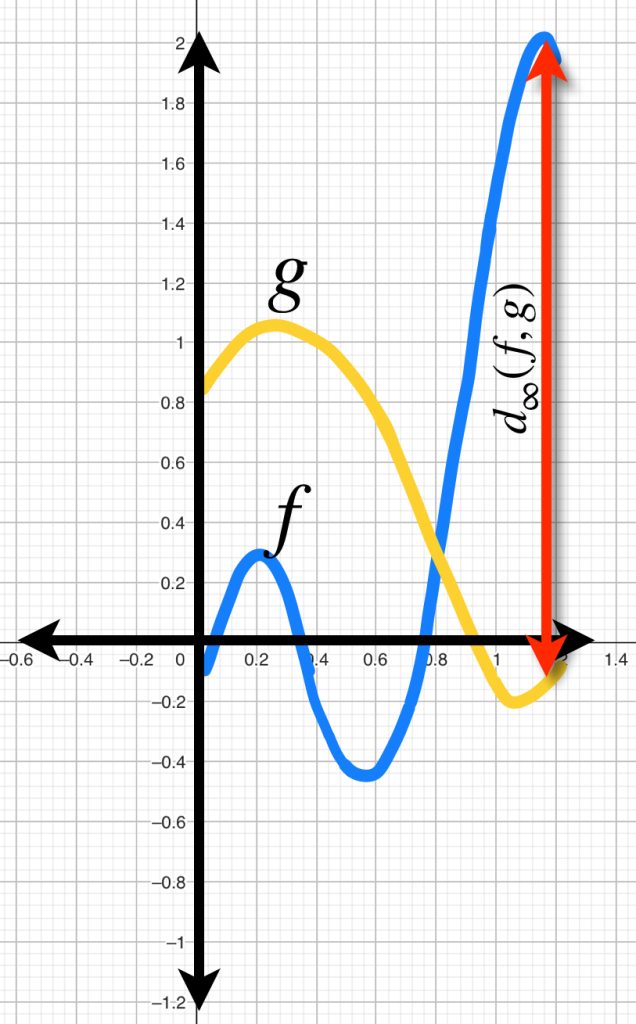
Esta no es la primera vez que hablamos de identificar distancias entre una función y otra. En la entrada Espacios de funciones definimos el espacio $\mathcal{B}(A,X)$ cuyos elementos son funciones acotadas de un conjunto $A$ en un espacio $X$ y la métrica está dada por:
$$d_\infty(f,g)= \underset{a \in A}{sup \,} \, d(f(a),g(a)), \, f,g \in \mathcal{B}(A,X)$$
La convergencia uniforme de una sucesión de funciones acotadas es equivalente a la convergencia como elementos del espacio métrico de funciones $\mathcal{B}(A,X),$ es decir:
Proposición: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión en $\mathcal{B}(A,X).$ Entonces, $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f: A \to X$ en $A$ si y solo si $(f_n)_{n \in \mathbb{N}}$ converge a $f$ en $\mathcal{B}(A,X).$
Demostración (ida):
Sea $\varepsilon >0.$ Como $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f: A \to X$ en $A,$ existe $N \in \mathbb{N} \,$ tal que para cada $k \geq N$ se cumple que para cada $a \in A, \, d(f_k(a),f(a)) < \frac{\varepsilon}{2} .$
1. $f$ está en el espacio $\mathcal{B}(A,X):$
Como $f_N$ es acotada, existen $x_0 \in X$ y $M \in \mathbb{R}$ tales que para toda $a \in A,$
$d(f_N(a),x_0) \leq M$
En consecuencia $d(f(a),x_0) \leq d(f(a),f_N(a))+d(f_N(a),x_0) < \frac{\varepsilon}{2} + M < \varepsilon + M$
Y como esto es posible $\forall \varepsilon >0$ concluimos que $f$ es acotada.
2. $(f_n)_{n \in \mathbb{N}} \to f$ en $\mathcal{B}(A,X):$
Teniendo a $\varepsilon$ como cota superior del conjunto $\{ d(f_k(a),f(a)) : a \in A \}$ se sigue que $d_\infty(f_k,f)= \underset{a \in A}{sup \,} \, d(f_k(a),f(a)) \leq \frac{\varepsilon}{2} < \varepsilon ,$ lo cual demuestra que $(f_n)_{n \in \mathbb{N}}$ converge a $f$ en $\mathcal{B}(A,X).$
El regreso es análogo y se propone como ejercicio.
Definición. Sucesión uniformemente de Cauchy: Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones con $f_n:A \to X, \, n \in \mathbb{N}.$ Decimos que $(f_n)$ es uniformemente de Cauchy en $A,$ si para todo $\, \varepsilon >0$ existe $N \in \mathbb{N}$ tal que para todo $\, l,m \geq N$ y para todo $ \, a \in A,$
$$d(f_l(a),f_m(a))< \varepsilon .$$
Nota que en la definición solo se menciona que las funciones de la sucesión se vuelven arbitrariamente cercanas dos a dos (en cualquier punto del dominio), a partir de alguna función.
La siguiente imagen muestra una sucesión uniformemente de Cauchy.
¿Cuándo podremos decir que una sucesión de funciones con esta propiedad converge de manera uniforme?
Para finalizar, veamos el siguiente resultado en espacios donde toda sucesión de Cauchy es convergente.
Teorema. Criterio de convergencia uniforme de Cauchy. Sea $(X,d)$ un espacio métrico completo. Una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ con $f_n:A \to X, \, n \in \mathbb{N}$ converge uniformemente en $A$ si y solo si $(f_n)_{n \in \mathbb{N}}$ es uniformemente de Cauchy en $A.$
Demostración:
Partamos de suponer que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $A$ a alguna función $f:A \to X.$ Sea $\varepsilon >0.$ Existe $N \in \mathbb{N}$ tal que para cada $l, m \geq N$ se cumple que para cada $a \in A$:
$$d(f_l(a),f_m(a)) \leq d(f_l(a),f_N(a))+d(f_N(a),f_m(a)) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon.$$
Por lo tanto $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente de Cauchy en $A.$
Ahora supón que $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente de Cauchy en $A.$ Sea $\varepsilon>0.$ Existe $N \in \mathbb{N}$ tal que para cada $l, m \geq N$ se cumple que para cada $a \in A, \, d(f_l(a),f_m(a))< \varepsilon.$ Esto significa que la sucesión $(f_n(a))_{n \in \mathbb{N}}$ (formada por los puntos de las funciones evaluadas en un $a \in A$ fijo) es de Cauchy. Como $X$ es completo, se sigue que $(f_n(a))_{n \in \mathbb{N}} \to L_a$ para algún $L_a \in X.$
Sea $f:A \to X$ tal que para cada $a \in A, \, f(a) = L_a.$ Queda como ejercicio al lector demostrar que $f$ es el límite uniforme de $(f_n)_{n \in \mathbb{N}}.$
Más adelante…
Observaremos sucesiones de funciones continuas que convergen. ¿Será continua la función límite? ¿Dependerá de si la convergencia es puntual o uniforme?
Tarea moral
- Para cada $n \in \mathbb{N}$ considera la función $n^x: \mathbb{R} \to \mathbb{R}.$ Donde tanto en el dominio como en el contradominio, $\mathbb{R}$ tiene la métrica euclidiana. Sea $a \in \mathbb{R}.$ Demuestra que:
a) Si $a<0$ entonces $(n^a)_{n \in \mathbb{N}}$ es convergente. ¿Cuál es el límite?
b) Si $a >0$ entonces $(n^a)_{n \in \mathbb{N}}$ tiende a infinito.
c) ¿Qué ocurre con la sucesión cuando $a=0?$ - Consideremos la misma sucesión de funciones $(n^x)_{n \in \mathbb{N}} \,$ pero ahora con dominio $(- \infty, a]$ con $a < 0.$ Sea $\varepsilon >0$. Toma el $N_a \in \mathbb{N}$ que satisface que $\forall n\geq N_a, \, d(f_n(a),0) < \varepsilon$ el cual existe, pues $f_n(a) \to 0.$ Demuestra que para todo $a^*<a$ también se cumple que $\forall n\geq N_a, \, d(f_n(a^*),0) < \varepsilon$ y por tanto la convergencia en $(- \infty,a]$ es uniforme.
- Demuestra el regreso de la siguiente proposición:
Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión en $\mathcal{B}(A,X).$ Entonces, $(f_n)_{n \in \mathbb{N}}$ converge uniformemente a $f: A \to X$ en $A$ si y solo si $(f_n)_{n \in \mathbb{N}}$ converge a $f$ en $\mathcal{B}(A,X).$ - En la demostración del criterio de convergencia uniforme de Cauchy, demuestra que $f$ como fue definida, es el límite uniforme de $(f_n)_{n \in \mathbb{N}}.$
- Supón que para cada $x \in A$ se cumple que $\underset{n \in \mathbb{N}}{lim} \, f_n(x) =f(x).$ Si definimos $M_n$ como $M_n=\underset{n \in \mathbb{N}}{sup} \, \, d(f_n(x),f(x))$ entonces $f_n \to f$ de manera uniforme si y solo si $M_n \to 0$ en $\mathbb{R}.$
Enlaces:
- Análisis Matemático.
- Enlace a entrada anterior.
- Enlace a entrada siguiente.