Introducción

Se discutirán a través de esta unidad teoremas selectos debido a su importancia en la solución de otros problemas, en esta nota será el Teorema de Stewart.

Teorema de Stewart

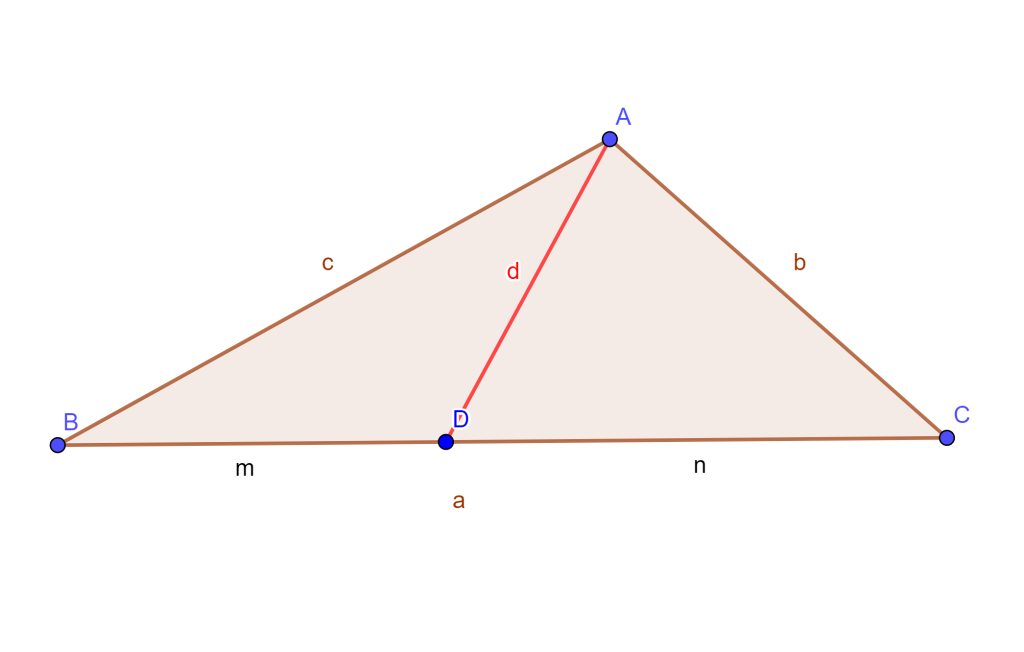
Teorema. Sea el triángulo $ABC$ con lados $BC,CA,AB$ los cuales sus longitudes son $a,b,c$ respectivamente, y sea un punto $D$ cualquiera en $BC$ donde $BC=m$ y $DC=n$, además si la longitud de $AD=d$, entonces

$ad^2=mb^2+nc^2-amn.$

Demostración Aplicando la Ley de cosenos a los triángulos $\triangle ABD$ en el ángulo $\angle ADB $ y el $\triangle ADC$ en el ángulo $\angle ADB$, se tiene

$c^2=d^2+m^2-2dm cos \angle ADB$
y
$b^2=d^2+n^2+2dn cos \angle ADB.$

Si multiplicamos ambas ecuaciones por $n$ y $m$ respectivamente tenemos:

$nc^2=nd^2+nm^2-2dnm cos \angle ADB$
y
$mb^2=md^2+mn^2+2dnm cos \angle ADB.$

Sumando ambas ecuaciones se tiene:

$nc^2+mb^2=nd^2+md^2+nm^2+mn^2.$

Ahora como $m+n=a$, se tiene:

$nc^2+mb^2=(n+m)d^2+(n+m)mn$
$nc^2+mb^2=ad^2+amn.$

Por lo tanto, concluimos que:

$ad^2=mb^2+nc^2-amn.$

$\square$

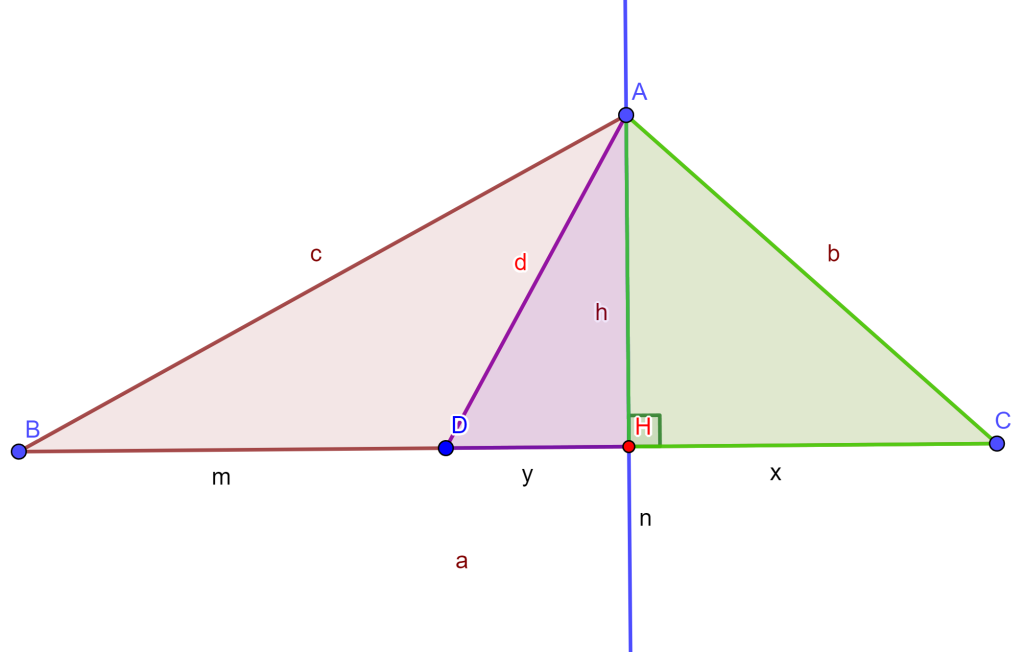
Demostración. (Por Pitágoras) Se tiene la altura de $A$ a $BC$ que corta en el punto $H$, donde $AH=h$, $CH=x$, $HD=y$.

Aplicando el Teorema de Pitágoras al triángulo $\triangle AHC$, $\triangle AHD$ y al $\triangle AHB$ se tiene lo siguiente respectivamente:

$b^2=x^2+h^2$ , $d^2=h^2+y^2$ y $c^2=h^2+(m+y)^2.$

Además se tiene que $y+x=n$ entonces $x=n-y$. Si lo sustituimos en $b^2=h^2+x^2$ se tiene $b^2=h^2+(n-y)^2$ y lo multiplicamos por $m$:

$mb^2=mh^2+m(n-y)^2.$

De igual forma multipliquemos $c^2=h^2+(m+y)^2$ por $n$:

$nc^2=nh^2+n(m+y)^2.$

Entonces sumando $md^2 + nc^2$ se tiene:

$mb^2+nc^2=mh^2+m(n-y)^2+nh^2+n(m+y)^2$
$mb^2+nc^2=(m+n)h^2+m(n^2-2ny+y^2)+n(m^2+2my+y^2)$
$mb^2+nc^2=(m+n)h^2 + mn^2-2mny+my^2+nm^2+2mny+ny^2$
$mb^2+nc^2=(m+n)h^2+mn^2+nm^2+my^2+ny^2$
$mb^2+nc^2=mn(n+m)+(m+n)(y^2+h^2)$
$mb^2+nc^2=(m+n)[mn+y^2+h^2].$

Sustituyendo $d^2=h^2+y^2$ y $m+n=a$ en la ecuación resultante:

$mb^2+nc^2=a[mn+d^2].$

Por lo tanto,

$ad^2=mb^2+nc^2-amn.$

$\square$

Conclusión

Es gracias a este Teorema que se puede encontrar la longitud de la recta $AB$ cuando $D$ es un punto cualquiera en la recta $BC$ y se tiene la razón en la cual $D$ divide a $BC$, ya que se conocen las longitudes y signos de $BD$ y $DC$ en este caso.
De igual forma, las longitudes de las medianas, las simedianas y las bisectrices de los ángulos de un triángulo, se pueden encontrar usando el Teorema de Stewart.

Con el uso del teorema de Stewart se puede resolver el siguiente Teorema.

Teorema. Si las bisectrices de dos ángulos interiores de un triángulo son iguales, el triángulo es isósceles.

Más adelante…

Se abordará el Teorema de Miquel.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Los tres problemas famosos
• Siguiente entrada del curso: Teorema de Miquel

Introducción

Las construcciones con regla y compas nos traen consigo problemas que no son posibles de resolverse a menos que se den consigo ciertas restricciones, es por eso que se abordaran construcciones, ya sea únicamente con regla o compas, y se darán construcciones de segmentos con longitud específica.

Construcciones con únicamente regla

Problema. Dibujar una recta paralela a otra recta dada con únicamente regla no es posible, a menos que en la recta dada existan tres puntos $A,B,C$ tal que $AB=BC$, entonces es posible trazar una recta paralela con regla a la recta dada por cualquier punto $P$ exterior a esa recta.

Construcción. Sea la recta $l$ con tres puntos $A,B,C$ los cuales cumplen $AB=BC$, y un punto exterior $P$. Tracemos la recta $PA$ y $PC$ y dibujemos una recta arbitraria que pase por $B$ y corte a estas rectas en $Q$ y $S$, entonces $AS$ y $CQ$ se intersecaran en $R$, y al trazar la recta $PR$ esta será la paralela buscada.

$\square$

Problema. Si dos rectas son paralelas, un segmento en una de ellas puede bisecarse únicamente con regla.

Construcción. Dadas dos rectas paralelas $l$ y $m$, donde en $l$ tomemos un segmento arbitrario $AC$. Tomemos dos puntos arbitrarios $P$ y $R$ en $m$ ($P \neq R$), tracemos las rectas $AP$ y $RC$ que se intersecan en $Q$. Tracemos las rectas $PC$ y $RA$ que se intersecan en $S$ y si dibujamos la recta $QS$ esta interseca a $AC$ en $B$ el cual es el punto buscado para bisecar el segmento $AC$.

$\square$

Problema. Trazar una recta por un punto dado paralela a dos rectas paralelas dadas con regla solamente.

Construcción. Usando la construcción del problema 2 nos dará un segmento bisecado de una de las rectas paralelas, de esta forma se obtiene lo necesario para aplicar la construcción del problema 1 y obtener una recta paralela a las dos paralelas dadas.

$\square$

Construcciones con regla y circunferencia dada

Steiner demostró que toda construcción puede hacerse con regla solamente si se dan en el plano de construcción una circunferencia y su centro.
Es por ello que se mostraran algunos problemas importantes.

Problema. Por un punto $P$ construir una recta paralela a una recta dada.

Construcción. Sea $E$ un punto sobre la recta $l$ y una circunferencia concentro $O$. Trace la recta $EO$ de tal forma fija que corte la circunferencia en los puntos $Q$ y $R$.

Ahora como $RO=OQ$ entonces por la construcción ya realizada anteriormente se puede trazar una paralela $AB$ a $OQ$, donde $AB$ es una cuerda. Si trazamos las rectas $AO$ y $OB$ estas cortarán en $A’$ y $B’$ respectivamente, formando los diámetros $AA’$ y $BB’$ los cuales determinan la cuerda $A’B’$.

Ahora $AB$ y $A’B’$ cortan a $l$ en $D$ y $F$ respectivamente, y en donde $DE=EF$. Y con esto se tiene lo necesario para construir una recta por $P$ que es paralela a $l$, ya que la construcción ya se ha hecho antes.

$\square$

Problema. Por un punto $P$ construya una recta perpendicular a una recta dada.

Construcción. Sea $E$ un punto de la recta, $l$ y $O$ el centro de una circunferencia fija. Si unimos $E$ con $O$ esta recta cortará a la circunferencia en dos puntos $R$ y $Q$.

Por construcciones anteriores se puede trazar una recta paralela a $l$ por $R$, que será la cuerda $RS$. Por lo cual $QS$ es perpendicular a $l$ y $RS$.

Ahora solo falta dibujar por $P$ una recta paralela a $QS$, pero usando la construcción del problema 1 se puede encontrar esta recta paralela a $QS$ y además perpendicular a $l$.

$\square$

Geometría Mascheroni del compás

Los geómetras L. Mascheroni y G. Mohr mencionan el teorema Mohr-Mascheroni: Todas las construcciones geométricas posibles, con regla y compas, pueden hacerse con compas solamente. Es interesante ver como con únicamente compas se pueden hacer construcciones más fáciles, y además se tiene que un hecho es que se ve una recta como construida cuando se hallan dos puntos de esta.
Es por ello que se mostraran algunas construcciones solo con el compás.

Problema. Construir el punto simétrico de un punto $C$ respecto a una recta $AB$.

Construcción. Se requiere dibujar las circunferencias con centros $A$ y $B$, y con radio $AC$ y $BC$ respectivamente. De esta forma se tendrá la intersección en el punto $C$ y además en otro punto $D$, el cual es el simétrico de $C$.

$\square$

Problema. Construir un segmento $n$ veces más grande que un segmento dado $AA_1$, $n=2,3,4,…$.

Construcción. Dibujemos dos circunferencias $C(A_1,AA_1)$ y $C(A,AA_1)$ las cuales se intersecan en un punto $B$, ahora trazamos otras dos circunferencias $C(A_1,AA_1)$ y $C(B,AA_1)$ las cuales se intersecan en un punto $C$. Si dibujamos una circunferencia $C(C,AA_1)$ esta interseca a $C(A_1,AA_1)$ en un punto $A_2$, estos puntos $A,A_1$ y $A_2$ son colineales donde $AA_2=2AA_1$. Repitiendo este proceso se obtiene los resultados buscados.

$\square$

Problema. Construir una cuarta proporcional a tres segmentos de rectas dadas.

Construcción. Sean $a,b,c$ los tres segmentos dados, dibujemos las circunferencias $C(O,a)$ y $C(O,b)$ donde $O$ es un punto cualquiera en el plano. Ahora, tomando un punto cualquiera $P$ de la $C(O,a)$ dibujemos un arco con $P$ centro y radio $c$, la cual interseca a $C(O,a)$ en $Q$.
Tomemos ahora un radio conveniente y $P$ y $Q$ dos centros, dibujaremos arcos que intersecan la circunferencia $C(O,b)$ en $P’$ y $Q’$ respectivamente. Donde $P’Q’$ es la cuarta proporcional buscada, esto debido a que se tiene semejanza de los triángulos $OPQ$ y $OP’Q’$, viene dada por la semejanza de los triángulos $OPP’$ y $OQQ’$.

$\square$

Problema. Dividir el arco $AB$ de la circunferencia por la mitad (centro conocido).

Construcción. Sea la circunferencia $C(O,r)$, supongamos que $OA=OB=r$ y $AB=a$.
Dibujemos las circunferencias $C(O,a)$, $C(O,r)$ y $C(B,r)$, y se tendrán las intersecciones $C$ y $D$.
Trazar las circunferencias $C(C,B)$ y $C(D,A)$ con intersección en $E$.
Dibujemos las circunferencias $C(C,OE)$ y $C(D,OE)$, de los cuales se tendrán las intersecciones en los puntos $X$ y $X’$.
El punto $X$ divide el arco $AB$ por la mitad y $X’$ divide por la mitad el arco que completa el primer arco hasta la circunferencia total.

$\square$

Construcción de segmentos con longitud específica

Si nos dieran un segmento de longitud 1, ¿Qué otras longitudes se pueden construir? Es por ello que veremos qué longitudes podemos construir, pero para ello debemos tener en cuenta que las construcciones deben utilizar solo una regla y un compás, y con un número finito de pasos.
Es fácil ver que dado el segmento de longitud 1, se puede construir un segmento de longitud $n$ ($n$ es un entero positivo) y de igual forma se pueden construir segmentos $p+q$ y $p-q$ donde $p$ y $q$ son segmentos de longitud dada.
¿Qué pasa con los segmentos de longitud $p/q$ ó $pq$?

Problema. Dado los segmentos de longitud 1,$p$ y $q$ construir el segmento de longitud $p/q$.

Construcción. Construir un segmento $AB$ con longitud $q$.
Construir un segmento $BC$ con longitud $p$, donde se tendrá el triángulo $ABC$.
En el segmento $AB$, pasa un segmento $AD$ de longitud 1.
Por el punto $D$, construir una recta paralela a $BC$ que corte a $AC$ en $E$.
Entonces $DE$ es de longitud $p/q$, debido a que $\triangle ABC \sim \triangle ADE$.

$\frac{p}{x} = \frac{q}{1}$ $\Rightarrow$ $\frac{p}{q}=\frac{x}{1}=x=DE.$

$\square$

Problema. Dado un segmento de longitud $p$ y $q$, construir un segmento de longitud $\sqrt{pq}$.

Construcción. Se usará la potencia de un punto para su construcción.

Dibujar un segmento $AB$ de longitud $p+q$, con $D$ el punto donde $AD=p$ y $DB=q$.
Trazar la circunferencia con $AB$ como diámetro.
Dibujar la cuerda $CE$ perpendicular a $AB$ en $D$, donde $CD$ es de longitud $\sqrt{pq}$.
Dado que $CE$ es perpendicular a $AB$, entonces $CD=DE$. Y por potencia de puntos en $D$, se tiene

$ CD \bullet DE = AD \bullet DB$
$CD \bullet CD = CD^2 = pq$
$CD = \sqrt{pq}.$

$\square$

Números Construibles

Un número $x$ es construible si, a partir de un segmento de longitud 1, se puede construir el segmento de longitud $x$ (con regla y compas).
Como por ejemplo $4/7$ es número construible, ya que gracias al segmento de longitud 1 se pueden construir los segmentos de longitud 4 y 7, y de esto se construye el segmento $4/7$.

Teorema. (Números Construibles) Si los números no negativos $a$ y $b$ son construibles, entonces también lo son los números

$a+b$, $a-b$, $a/b$ $(b \neq 0)$, $ab$, $\sqrt{a}$

Se pueden construir muchos números construibles, a partir de estas operaciones.

Ejemplos:

$5$ y $4$ son construibles, entonces $\sqrt{5}$ y $\sqrt{4}$ también.
$3$ y $\sqrt{4}$ son construibles, entonces $3+ \sqrt{4}$ es construible.
$3+\sqrt{4}$ es construible, entonces $\sqrt{3+\sqrt{4}}$ es construible.
$\sqrt{3+\sqrt{4}}$ y $\sqrt{5}$ son construibles, entonces $\frac{\sqrt{5}}{\sqrt{3+\sqrt{4}}}$ es construible.

Es así que tomando el número 1 como inicio, y haciendo finitas sucesiones de adiciones, substracciones, raíces, productos y proporciones, es que podemos obtener todos los números construibles.

Alguno de los números que no son construibles son

$\pi, e , \sqrt[3]{2}, cos20^o.$

$\triangle$

Esto explicaría por qué los tres problemas famosos no pueden ser resueltos.

Más adelante…

Se abordarán los tres problemas famosos, para mostrar su imposibilidad debido al uso único de regla y compas.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Ejercicios de la Unidad 4
• Siguiente entrada del curso: Los tres problemas famosos