Introducción

En esta entrada abordaremos el concepto de diferenciabilidad desde un enfoque complejo, es decir, definiremos lo que entenderemos por la derivada de una función compleja, lo cual nos será de gran utilidad para caracterizar a $\mathbb{C}$ y a las funciones complejas que posean derivadas en el sentido complejo, con lo cual quedará claro que la diferenciabilidad compleja es más estricta que la diferenciabilidad estudiada sobre ${\mathbb{R}}^2$.

Al hablar de funciones complejas y sus derivadas, algunos textos usan los términos «holomorfa» y «analítica» de forma indistinta, al referirse a la diferenciabilidad de dichas funciones, mientras que otros utilizan «diferenciable» o «complejo diferenciable» y «holomorfa» de forma indistinta. El uso del término «analítica» se debe al hecho de que una función «holomorfa» tiene una expansión en series de potencias locales en cada punto de su dominio. De hecho, esta propiedad de la expansión en series de potencias es una caracterización completa de las funciones holomorfas, la cual se discutirá a detalle más adelante. Por otra parte, el uso del término «complejo diferenciable» surge por las propiedades relacionadas con la derivada compleja. En otros textos más antiguos se suelen utilizar los términos «regular» y «monogénica».

Las funciones holomorfas son una generalización de los polinomios complejos, pero resultan ser objetos matemáticos mucho más flexibles que los polinomios. El conjunto de los polinomios complejos es cerrado bajo la suma y la multiplicación, mientras que el conjunto de las funciones holomorfas es cerrado no solo bajo la suma y la multiplicación, sino también bajo recíprocos, inversas, exponenciación, logarítmos, raíces cuadradas y muchas otras operaciones.

Otro término que suele usarse al hablar de funciones holomorfas es el de «conforme» o «trasformación conforme», el cual se debe a una propiedad geométrica muy importante de dichas funciones que estudiaremos a detalle en las siguientes entradas. La conformidad es una propiedad que permite modelar el flujo de los fluidos incompresibles y otros fenómenos físicos mediante las funciones holomorfas.

Definición 16.1. (Diferenciabilidad compleja.)
Sea $U\subset \mathbb{C}$ un conjunto abierto, sea $z_0\in U$ y sea $f:U\to \mathbb{C}$ una función. Diremos que $f$ es complejo diferenciable o $\mathbb{C}$-diferenciable en $z_0$ si existe el límite: $$\begin{array}{}\text{(16.1)}& \underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}},\end{array}$$ y en caso de existir, a dicho límite se le llama la derivada compleja, o simplemente la derivada, de $f$ en $z_0$, la cual se denota como $f^{\prime }(z_0)$, $\frac{df}{dz}(z_0)$ o $\frac{d}{dz}f(z_0)$. Si $f$ posee derivada en todo punto de $U$, entonces diremos que $f$ es holomorfa en $U$ y denotamos al conjunto de funciones holomorfas en $U$ como: $$\mathcal{H}(U)=\{f:U\to \mathbb{C}:f\text{es holomorfa en}U\}.$$

Observación 16.1.
Para definir el concepto de derivada compleja no es necesario pedir que $U$ sea un conjunto abierto, sino que basta con considerar a $z_0\in U\cap U^{\prime }$ para que la definición anterior sea válida. Sin embargo esta generalización carece de importancia para la teoría, por lo que en general siempre que se hable de funciones diferenciables en el sentido complejo se considerarán conjuntos abiertos en $\mathbb{C}$.

Observación 16.2.
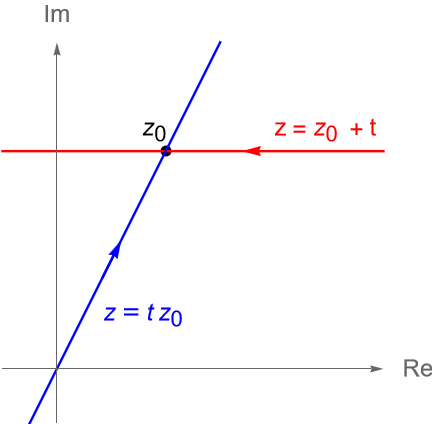
Tomando $z=z_0+h$, podemos reescribir el límite (16.1) como: $$\begin{array}{}\text{(16.2)}& \underset{h\to 0}{lim}{\displaystyle \frac{f(z_0+h)–f(z_0)}{h}},\end{array}$$ notemos que tanto en (16.1) como en (16.2) se observa una definición similar a la de la derivada de una función real, sin embargo debe ser claro que en el caso real utilizando (16.1) tenemos que $x$ solo puede aproximarse a $x_0$ en dos direcciones, por la izquierda o por la derecha, análogamente si consideramos (16.2) tenemos que $h$ solo puede aproximarse a $0$ en dichas direcciones, mientras que en el caso complejo esto no se cumple, ya que sin importar cual de los dos límites utilicemos, es claro que $z$ puede aproximarse a $z_0$ y/o $h$ puede aproximarse a $0$ en más de dos direcciones, por lo que la existencia de la derivada de una función compleja no dependerá de la dirección en que $z$ se aproxime a $z_0$ y/o $h$ se aproxime a $0$, figura 71.

Definición 16.2. (Analicidad.)
Sean $S\subset \mathbb{C}$ y $f:S\to \mathbb{C}$ una función.

1. Si $z_0$ es un punto interior de $S$, entonces diremos que $f$ es analítica en $z_0\in S$, si $f$ es holomorfa en $B(z_0,\rho )\subset S$ para algún $\rho >0$, es decir si en $S$ existe algún $\rho$-vecindario de $z_0$, donde $f$ es holomorfa. Diremos que $f$ es analítica en $S$ si existe algún conjunto abierto totalmente contenido en $S$ donde $f$ es analítica.
2. Si $S=\mathbb{C}$, entonces diremos que $f$ es entera si $f$ es analítica en $\mathbb{C}$.

Observación 16.3.
A partir de las definiciones 16.1 y 16.2 es claro que para $U\subset \mathbb{C}$ un conjunto abierto, una función $f:U\to \mathbb{C}$ será analítica en $U$ si es analítica en cada punto $z\in U$, por lo que durante el curso utilizaremos de manera indistinta los términos analítica y holomorfa para referirnos a funciones $\mathbb{C}$-diferenciables en conjuntos abiertos en $\mathbb{C}$. Sin embargo, más adelante veremos que la definición 16.2 será de gran utilidad al trabajar con funciones dadas por series de potencias.

Observación 16.4.
Notemos que si una función $f(z)$ es holomorfa en $U\subset \mathbb{C}$, entonces $f^{\prime }(z)$ define una función $f^{\prime }:U\to \mathbb{C}$. Si $f^{\prime }(z)$ es continua, entonces se dice que $f(z)$ es continuamente diferenciable. Si $f^{\prime }(z)$ es holomorfa en $U$, entonces se dice que $f(z)$ es dos veces diferenciable en $U$. Continuando de esta manera, tenemos que una función $f$ tal que cada una de sus derivadas sucesivas es nuevamente diferenciable es llamada infinitamente diferenciable. Este concepto es de suma importancia pues de manera equivalente se puede definir a una función $f:U\to \mathbb{C}$ como analítica en $U$ si $f(z)$ es continuamente diferenciable en $U$. De hecho, más adelante veremos que a diferencia de las funciones reales, en el caso complejo la existencia de $f^{\prime }(z)$ garantiza la existencia de todas las derivadas de $f(z)$, lo cual no sucede en el caso real, por ejemplo para la función $f(x)=|x|x$ es claro que $f^{\prime }(x)=2|x|$ existe para todo $x\in \mathbb{R}$, pero $f^{”}(x)$ no existe para $x=0$.

Ejemplo 16.1.
a) Sea $f:\mathbb{C}\to \mathbb{C}$ tal que $f(z)=c$, con $c\in \mathbb{C}$ constante, entonces $f$ es entera en $\mathbb{C}$.

Solución. Sea $z_0\in \mathbb{C}$, entonces: $$\begin{array}{rl}{f}^{\prime }(z_0)& =\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}\\ & =\underset{z\to z_0}{lim}{\displaystyle \frac{c–c}{z-z_0}}\\ & =0.\end{array}$$

b) Sea $f:\mathbb{C}\to \mathbb{C}$ tal que $f(z)=(3-i)z$, entonces $f$ es entera en $\mathbb{C}$.

Solución. Sea $z_0\in \mathbb{C}$, entonces: $$\begin{array}{rl}{f}^{\prime }(z_0)& =\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}\\ & =\underset{z\to z_0}{lim}{\displaystyle \frac{(3-i)z–(3-i)z_0}{z-z_0}}\\ & =3-i.\end{array}$$

c) Sea $f:\mathbb{C}\to \mathbb{C}$ tal que $f(z)=z^3$, entonces $f$ es entera en $\mathbb{C}$.

Solución. Sea $z_0\in \mathbb{C}$, entonces: $$\begin{array}{rl}{f}^{\prime }(z_0)& =\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}\\ & =\underset{z\to z_0}{lim}{\displaystyle \frac{z^3–z_0^3}{z-z_0}}\\ & =\underset{z\to z_0}{lim}{\displaystyle \frac{(z-z_0)(z^2+z{z}_0+z_0^2)}{z-z_0}}\\ & =3z_0^2.\end{array}$$

Del inciso a) tenemos que para $f(z)=c$, con $c\in \mathbb{C}$ constante, se tiene que $f^{\prime }(z)=0$, para todo $z\in \mathbb{C}$.

Por otra parte, del inciso b) tenemos que en general para $c\in \mathbb{C}$ constante, se cumple que si $f(z)=cz$, entonces $f^{\prime }(z)=c$, para todo $z\in \mathbb{C}$.

Veamos ahora que el concepto de diferenciabilidad y analicidad no son intercambiables, es decir puede pasar que una función sea diferenciable en $z_0$, pero que no sea analítica en dicho punto.

Ejemplo 16.2.
Sea $f:\mathbb{C}\to \mathbb{C}$ dada por $f(z)={\bar{z}}^2$. Veamos que dicha función es diferenciable en $z_0=0$ y que no es diferenciable en ningún $z_0\ne 0$, en particular veamos que $f$ no es analítica en $z_0=0$.

Solución. Si $z_0=0$, entonces: $$\begin{array}{rl}{f}^{\prime }(z_0)& =\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}\\ & =\underset{z\to 0}{lim}{\displaystyle \frac{{\bar{z}}^2–0}{z-0}}\\ & =\underset{z\to 0}{lim}{\displaystyle \frac{{\bar{z}}^2}{z}}\\ & =0.\end{array}$$ Veamos que si $z_0\ne 0$, entonces el límite que define a la derivada no existe. Primeramente, si nos aproximamos a $z_0$ a través de la recta que pasa por $0$ y que tiene dirección $z_0$, figura 72, es decir: $$z=t{z}_0,t\in \mathbb{R},$$ entonces: $$\begin{array}{rl}\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}& =\underset{t\to 1}{lim}{\displaystyle \frac{{\overline{t{z}_0}}^2–{\overline{z_0}}^2}{t{z}_0-z_0}}\\ & =\underset{t\to 1}{lim}{\displaystyle \frac{{\left(\overline{z_0}\right)}^2\left(t^2–1\right)}{z_0(t-1)}}\\ & ={\displaystyle \frac{{\overline{z_0}}^2}{z_0}}\underset{t\to 1}{lim}(t+1)\\ & =2{\displaystyle \frac{{\overline{z_0}}^2}{z_0}}.\end{array}$$ Por otra parte tenemos que si nos aproximamos a $z_0$ a través de la recta paralela al eje real que pasa por $z_0$, figura 72, es decir: $$z=z_0+t,t\in \mathbb{R},$$ entonces:
$$\begin{array}{rl}\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}& =\underset{t\to 0}{lim}{\displaystyle \frac{{\overline{(z_0+t)}}^2–{\overline{z_0}}^2}{t}}\\ & =\underset{t\to 0}{lim}{\displaystyle \frac{(\overline{z_0}+t{)}^2–{\overline{z_0}}^2}{t}}\\ & =\underset{t\to 0}{lim}{\displaystyle \frac{2t\overline{z_0}+t^2}{t}}\\ & =\underset{t\to 0}{lim}(2\overline{z_0}+t)\\ & =2\overline{z_0}.\end{array}$$ Desde que estos dos límites son distintos y $z_0\ne 0$ es arbitrario, concluimos que para $z_0\ne 0$ la función no es diferenciable, por lo que en $z_0=0$ la función no es analítica ya que no existe vecindad de $z_0=0$ donde $f^{\prime }(z_0)$ exista.

Ejemplo 16.3.
Veamos que las siguientes funciones no son analíticas en ningún punto de $\mathbb{C}$.
a) $f(z)=\bar{z}$.
b) $f(z)=\mathrm{Re}(z)$.

Solución. Sea $z_0\in \mathbb{C}$. Para verificar la afirmación basta con mostrar que el límite que define a la derivada no existe para todo $z_0\in \mathbb{C}$, para ello nos aproximaremos a $z_0$ a lo largo de las rectas utilizadas en el ejemplo 16.2, figura 72.

a) Si nos aproximamos a $z_0$ a través de la recta $z=t{z}_0$, con $t\in \mathbb{R}$, tenemos que: $$\begin{array}{rl}\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}& =\underset{t\to 1}{lim}{\displaystyle \frac{\overline{t{z}_0}–\overline{z_0}}{t{z}_0-z_0}}\\ & =\underset{t\to 1}{lim}{\displaystyle \frac{\overline{z_0}\left(t–1\right)}{z_0(t-1)}}\\ & ={\displaystyle \frac{\overline{z_0}}{z_0}}.\end{array}$$ Mientras que si nos aproximamos a $z_0$ a través de la recta $z=z_0+t$, con $t\in \mathbb{R}$, tenemos que: $$\begin{array}{rl}\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}& =\underset{t\to 0}{lim}{\displaystyle \frac{\overline{(z_0+t)}–\overline{z_0}}{t}}\\ & =\underset{t\to 0}{lim}{\displaystyle \frac{\overline{z_0}+t–\overline{z_0}}{t}}\\ & =1.\end{array}$$ Como estos límites son distintos y $z_0\in \mathbb{C}$ es arbitrario, entonces concluimos que no existe $f^{\prime }$ para ningún punto de $\mathbb{C}$, por lo que $f(z)=\bar{z}$ no es analítica en $\mathbb{C}$.

b) Si nos aproximamos a $z_0$ a través de la recta $z=t{z}_0$, con $t\in \mathbb{R}$, tenemos que: $$\begin{array}{rl}\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}& =\underset{t\to 1}{lim}{\displaystyle \frac{\mathrm{Re}(t{z}_0)–\mathrm{Re}(z_0)}{t{z}_0-z_0}}\\ & =\underset{t\to 1}{lim}{\displaystyle \frac{\mathrm{Re}(z_0)(t-1)}{z_0(t-1)}}\\ & ={\displaystyle \frac{\mathrm{Re}(z_0)}{z_0}}.\end{array}$$ Mientras que si nos aproximamos a $z_0$ a través de la recta $z=z_0+t$, con $t\in \mathbb{R}$, tenemos que: $$\begin{array}{rl}\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z-z_0}}& =\underset{t\to 0}{lim}{\displaystyle \frac{\mathrm{Re}(z_0+t)–\mathrm{Re}(z_0)}{t}}\\ & =\underset{t\to 0}{lim}{\displaystyle \frac{\mathrm{Re}(z_0)+t–\mathrm{Re}(z_0)}{t}}\\ & =1.\end{array}$$ Dado que estos límites son distintos y $z_0\in \mathbb{C}$ es arbitrario, entonces concluimos que no existe $f^{\prime }$ para ningún punto de $\mathbb{C}$, por lo que $f(z)=\mathrm{Re}(z)$ no es analítica en $\mathbb{C}$.

Proposición 16.1.
Sean $U\subset \mathbb{C}$ un conjunto abierto y $f:U\to \mathbb{C}$ una función analítica, entonces $f$ es continua en $U$.

Demostración. Dado que $f$ es analítica en $U$, sabemos que $f^{\prime }(z)$ existe para todo $z\in U$, entonces de acuerdo con la proposición 14.3(2) se cumple que el límite de un producto es el producto de los límites, por lo que: $$\begin{array}{rl}\underset{z\to z_0}{lim}(f(z)–f(z_0))& =\underset{z\to z_0}{lim}\frac{f(z)–f(z_0)}{z–z_0}(z-z_0)\\ & =\underset{z\to z_0}{lim}\frac{f(z)–f(z_0)}{z–z_0}\underset{z\to z_0}{lim}(z-z_0)\\ & =f^{\prime }(z_0)\cdot 0\\ & =0,\end{array}$$ de donde se tiene que $f$ es continua en $z_0$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 16.2. (Reglas de diferenciación.)
Sean $U\subset \mathbb{C}$ un conjunto abierto, $g,f:U\to \mathbb{C}$ dos funciones analíticas y $c_1,c_2\in \mathbb{C}$ dos constantes, entonces:

1. La función $c_{1}f+c_{2}g$ es analítica en $U$ y para todo $z\in U$ se tiene que: $$(c_{1}f(z)\pm c_{2}g(z){)}^{\prime }=c_1{f}^{\prime }(z)\pm c_2{g}^{\prime }(z).$$
2. La función $fg$ es analítica en $U$ y para todo $z\in U$ se tiene que: $$(f(z)g(z){)}^{\prime }=f^{\prime }(z)g(z)+f(z)g^{\prime }(z).$$
3. La función ${\displaystyle \frac{f}{g}}$ es analítica en $W=U\setminus \{z\in U:g(z)=0\}$ y para todo $z\in W$ se tiene que: $${\left(\frac{f(z)}{g(z)}\right)}^{\prime }=\frac{f^{\prime }(z)g(z)–f(z)g^{\prime }(z)}{(g(z){)}^2}.$$

Demostración.

1. Se deja como ejercicio al lector.
2. Dadas las hipótesis, para $z_0\in U$ tenemos, por la proposición 14.3(2) y la proposición 16.1, que: $$\begin{array}{rl}(f(z_0)g(z_0){)}^{\prime }& =\underset{z\to z_0}{lim}\frac{f(z)g(z)–f(z_0)g(z_0)}{z-z_0}\\ & =\underset{z\to z_0}{lim}\frac{f(z)g(z)–f(z_0)g(z)+f(z_0)g(z)–f(z_0)g(z_0)}{z-z_0}\\ & =\underset{z\to z_0}{lim}\frac{g(z)[f(z)–f(z_0)]+f(z_0)[g(z)–g(z_0)]}{z-z_0}\\ & =\underset{z\to z_0}{lim}g(z)\frac{f(z)–f(z_0)}{z-z_0}+\underset{z\to z_0}{lim}f(z_0)\frac{g(z)–g(z_0)}{z-z_0}\\ & =g(z_0)f^{\prime }(z_0)+f(z_0)g^{\prime }(z_0).\end{array}$$
3. Dadas las hipótesis, procedemos a realizar la prueba considerando $f(z)=1$ para todo $z\in U$, el caso general {\bf se deja como ejercicio al lector.} Sea $z_0\in W$, entonces $g(z_0)\ne 0$. Por la proposición 16.1 sabemos que $g$ es continua en $W$, por lo que, para $\epsilon =|g(z_0)|/2>0$ existe $\delta >0$ tal que si $|z–z_0|<\delta$, entonces: $$|g(z)–g(z_0)|<\frac{|g(z_0)|}{2},$$ de donde: $$0<\frac{|g(z_0)|}{2}<|g(z)|,$$ por lo que $g(z)\ne 0$.
   
   Entonces, para todo $z\in B(z_0,\delta )$, por la proposición 14.3(2) y la proposición 16.1, tenemos que: $$\begin{array}{rl}{\left(\frac{1}{g(z_0)}\right)}^{\prime }& =\underset{z\to z_0}{lim}\frac{\frac{1}{g(z)}–\frac{1}{g(z_0)}}{z-z_0}\\ & =\underset{z\to z_0}{lim}\frac{-1}{g(z)g(z_0)}\frac{g(z)-g(z_0)}{z-z_0}\\ & =-\frac{g^{\prime }(z_0)}{g(z_0{)}^2}.\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 16.4.
Sea $f:\mathbb{C}\to \mathbb{C}$ dada por $f(z)=z^n$, con $n\in {\mathbb{N}}^{+}$, veamos que $f$ es una función entera y que: $$\begin{array}{}\text{(16.3)}& \frac{d}{dz}{z}^n=n{z}^{n-1}.\end{array}$$

Demostración. Realizamos la prueba por inducción sobre $n$. Sea $n=1$, entonces $f(z)=z$, por lo que para $z_0\in \mathbb{C}$ tenemos que: $$\begin{array}{rl}{f}^{\prime }(z_0)& =\underset{z\to z_0}{lim}\frac{f(z)–f(z_0)}{z–z_0}\\ & =\underset{z\to z_0}{lim}\frac{z–z_0}{z–z_0}\\ & =1,\end{array}$$ de donde (16.3) se cumple para $n=1$.

Supongamos que (16.3) se cumple para $n=k$ con $k\in \mathbb{N}$ fijo. Veamos que (16.3) se cumple para $n=k+1$. Notemos que para $n=k+1$ se tiene que $f(z)=z^{k+1}=z^{k}z$, entonces para todo $z\in \mathbb{C}$, por la proposición 16.2(2), tenemos que: $$\begin{array}{rl}{f}^{\prime }(z)& =\frac{d}{dz}\left(z^{k+1}\right)\\ & =z\frac{d}{dz}(z^k)+z^k\frac{d}{dz}z\\ & =k{z}^{k-1}z+z^k\\ & =(k+1)z^k.\end{array}$$ Por lo que para todo $n\in {\mathbb{N}}^{+}$ se tiene que $f(z)=z^n$ es entera y su derivada está dada por (16.3).

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

De hecho se puede mostrar que si $f:\mathbb{C}\setminus \{0\}\to \mathbb{C}$ está dada por $f(z)=z^n$ y $n\in \mathbb{Z}$, entonces $f$ es analítica y su derivada está dada por (16.3), lo cual se deja como ejercicio al lector.

Ejemplo 16.5.
Sea $f_0(z)$ la rama principal de la función multivaluada $F(z)=\sqrt{z}$, es decir:
$$f_0(z)=\sqrt{z}=\sqrt{r}\mathrm{cis}\left(\frac{\theta (z)}{2}\right),$$ donde $r=|z|$, $\theta (z)=\mathrm{Arg}(z)$ y $z\in \mathbb{C}\setminus (-\mathrm{\infty },0]$.

Veamos que $f_0$ es analítica en el dominio $D=\mathbb{C}\setminus (-\mathrm{\infty },0]$ y determinemos su derivada.

Solución. De acuerdo con el ejemplo 15.7, sabemos que $f_0$ no es continua en $(-\mathrm{\infty },0]$, por lo que se sigue de la proposición 16.1 que en dicho conjunto $f_0$ no puede ser analítica.

Más aún, por la continuidad de $f_0$ en $D$, para $z_0\in D$ fijo tenemos que: $$\begin{array}{rl}{f}_0\prime (z_0)& =\underset{z\to z_0}{lim}\frac{\sqrt{z}–\sqrt{z_0}}{z-z_0}\\ & =\underset{z\to z_0}{lim}\frac{\sqrt{z}–\sqrt{z_0}}{\left(\sqrt{z}–\sqrt{z_0}\right)(\sqrt{z}+\sqrt{z_0})}\\ & =\underset{z\to z_0}{lim}\frac{1}{\sqrt{z}+\sqrt{z_0}}\\ & =\frac{1}{2\sqrt{z_0}}.\end{array}$$

Desde que $z_0\in D$ era arbitrario y $D$ es un dominio, en particular un conjunto abierto, concluimos que $f_0$ es analítica en $D$.

Es interesante notar que la derivada de la rama principal $f_0$ corresponde con la derivada de la función real $f(x)=\sqrt{x}$ con la que estamos familiarizados.

Corolario 16.1.
Sea $n\in \mathbb{N}$ y sean $c_i\in \mathbb{C}$, con $i\in \{0,1,\dots ,n\}$, constantes con $c_n\ne 0$. Entonces:

1. Todo polinomio de grado $n$, digamos $p(z)=c_0+c_{1}z+c_2{z}^2+\cdots +c_n{z}^n$, es una función entera y su derivada es: $$\begin{array}{}\text{(16.4)}& p^{\prime }(z)=c_1+2c_{2}z+\cdots +(n-1)c_{n-1}{z}^{n-2}+n{c}_n{z}^{n-1}.\end{array}$$
2. Toda función racional $f(z)={\displaystyle \frac{p(z)}{g(z)}}$, donde $p(z)$ y $g(z)$ son polinomios, es una función analítica para todos los puntos $z$ tales que $g(z)\ne 0$ y su derivada es: $$\begin{array}{}\text{(16.5)}& f^{\prime }(z)=\frac{p^{\prime }(z)g(z)+p(z)g^{\prime }(z)}{g(z{)}^2}.\end{array}$$

Demostración.

1. Dadas las hipótesis, procedemos a realizar la prueba por inducción sobre $n$. Si $n=0$ entonces $p(z)=c_0$ es una función constante y por tanto es una función entera tal que $p^{\prime }(z)=0$. Si $n=1$, entonces tenemos que $p(z)=c_0+c_{1}z$. De acuerdo con el ejemplo 16.4 y la proposición 16.2, tenemos que $p(z)$ es una función entera y su derivada es: $$p^{\prime }(z)=0+c_1(1)z^{1-1}=c_1,$$ por lo que para $n=1$ se cumple (16.4). Supongamos que el resultado es válido para $n=k$, con $k\in \mathbb{N}$ fijo. Para $n=k+1$ tenemos que: $$\begin{array}{rl}p(z)& =c_0+\sum _{n=1}^{k+1}{c}_n{z}^n\\ & =c_0+\sum _{n=1}^k{c}_n{z}^n+c_{k+1}{z}^{k+1},\end{array}$$ por hipótesis de inducción sabemos que $c_0+\sum _{n=1}^k{c}_n{z}^n$ es una función entera cuya derivada está dada por (16.4) y por el ejemplo 16.4 y la proposición 16.2 tenemos que $c_{k+1}{z}^{k+1}$ es también una función entera cuya derivada es $(k+1)c_{k+1}{z}^k$, entonces: $$p^{\prime }(z)=c_1+2c_{2}z+\cdots +(k-1)c_{k-1}{z}^{k-2}+k{c}_k{z}^{k-1}+(k+1)c_{k+1}{z}^k,$$ por lo que el resultado es válido para todo $n\in \mathbb{N}$.
2. De acuerdo con la proposición 16.2(3) y considerando el inciso anterior, es claro que una función racional $f(z)={\displaystyle \frac{p(z)}{g(z)}}$, con $p(z)$ y $g(z)$ polinomios, es una función analítica en su dominio de definición, es decir en $S=\{z\in \mathbb{C}:g(z)\ne 0\}$, cuya derivada está dada por (16.5).

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 16.6.
Determina la derivada de las siguientes funciones y en caso de ser necesario especifica en dónde es analítica la función.

a) $f(z)=3z^4–5z^3+2z$.

Solución. De acuerdo con el corolario 16.1 tenemos que $f$ es una función entera y su derivada es: $$f^{\prime }(z)=2(1)-5(3z^2)+3(4z^3)=12z^3-15z^2+2.$$ b) $f(z)={\displaystyle \frac{(z+1)(z+i{)}^2}{z+1-3i}}$.

Solución. De acuerdo con la proposición 16.2 tenemos que: $$\begin{array}{rl}{f}^{\prime }(z)& =\frac{((z+i{)}^2+2(z+1)(z+i))(z+1-3i)–(z+1)(z+i{)}^2}{(z+1-3i{)}^2}\\ & =\frac{2z^3+(4-7i)z^2+(14-2i)z+5i+6}{(z+1-3i{)}^2}.\end{array}$$ Por el corolario 16.1 tenemos que esta función es analítica en $S=\mathbb{C}\setminus \{-1+3i\}$, ya que en $z=-1+3i$ el denomidador de $f$ se anula.

c) $f(z)={\displaystyle \frac{z^2}{4z+1}}$.

Solución. Por la proposición 16.2 tenemos que: $$\begin{array}{rl}{f}^{\prime }(z)& =\frac{(4z+1)(2z–z^2(4))}{(4z+1{)}^2}\\ & =\frac{4z^2+2z}{(4z+1{)}^2}.\end{array}$$ De acuerdo con el corolario 16.1 tenemos que esta función es analítica en $S=\mathbb{C}\setminus \{-\frac{1}{4}\}$, ya que en $z=-\frac{1}{4}$ el denomidador de $f$ se anula.

Proposición 16.3. (Carathéodory.)
Sean $U\subset \mathbb{C}$ un conjunto abierto, $z_0\in U$ y $f:U\to \mathbb{C}$ una función. Entonces, $f$ es analítica en $z_0$ si y solo si existe una función $\phi :U\to \mathbb{C}$ continua en $z_0$ tal que para todo $z\in U$: $$f(z)=f(z_0)+\phi (z)(z-z_0).$$ En este caso $\phi (z_0)=f^{\prime }(z_0)$.

Demostración. Dadas las hipótesis, tenemos que:

$\Rightarrow )$
Si $f$ es analítica en $z_0$, entonces existe: $$f^{\prime }(z_0)=\underset{z\to z_0}{lim}\frac{f(z)–f(z_0)}{z-z_0}.$$ Sea $\phi :U\to \mathbb{C}$ dada por: $$\phi (z)=\{\begin{array}{lcc}{\displaystyle \frac{f(z)–f(z_0)}{z–z_0}}& \text{si}& z\ne z_0,\\ f^{\prime }(z_0)& \text{si}& z=z_0.\end{array}$$ Es claro que para todo $z\in U$, incluso para $z=z_0$, se tiene que: $$f(z)=f(z_0)+\phi (z)(z-z_0).$$ Por otra parte notemos que:
$$\underset{z\to z_0}{lim}\phi (z)=\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z–z_0}}=f^{\prime }(z_0)=\phi (z_0),$$ por lo que $\phi$ es continua en $z_0$ y $f^{\prime }(z_0)=\phi (z_0)$.

$(\Leftarrow$
Sea $\phi :U\to \mathbb{C}$ una función continua en $z_0$ tal que para todo $z\in U$: $$f(z)=f(z_0)+\phi (z)(z-z_0).$$ Por la continuidad de $\phi$ tenemos que: $$\phi (z_0)=\underset{z\to z_0}{lim}\phi (z)=\underset{z\to z_0}{lim}{\displaystyle \frac{f(z)–f(z_0)}{z–z_0}},$$ por lo que el límite que define a $f^{\prime }(z_0)$ existe y $f^{\prime }(z_0)=\phi (z_0)$, entonces $f$ es analítica en $z_0$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

De nuestros cursos de Cálculo, sabemos que otra de las reglas de diferenciación importantes es la regla de la cadena, por lo que podemos preguntarnos si dicho resultado es válido para funciones complejas dado que hemos visto que la composición de funciones es una operación posible para las funciones complejas, por lo que nos disponemos a responder a esta pregunta mediante el siguiente resultado.

Proposición 16.4. (Regla de la cadena.)
Sean $U_1,U_2\subset \mathbb{C}$ dos conjuntos abiertos, $g:U_1\to \mathbb{C}$ una función analítica en $U_1$ y $f:U_2\to \mathbb{C}$ una función analítica en $U_2$, tales que $g(U_1)\subset U_2$. Entonces $f\circ g$ es una función analítica en $U_1$ y para $z_0\in U_1$ se tiene que: $$\begin{array}{}\text{(16.6)}& (f\circ g{)}^{\prime }(z_0)=f^{\prime }(g(z_0))g^{\prime }(z_0).\end{array}$$

Demostración. Dadas las hipótesis, por la proposición 16.3 tenemos que si $g$ es analítica en $z_0\in U_1$ y $f$ es analítica en $w_0=g(z_0)\in U_2$, entonces existen funciones ${\phi }_1:U_1\to \mathbb{C}$ y ${\phi }_2:U_2\to \mathbb{C}$ continuas en $z_0$ y $w_0$, respectivamente, tales que: $$\begin{array}{r}g(z)=g(z_0)+{\phi }_1(z)(z-z_0),\mathrm{\forall }z\in U_1,\\ f(w)=f(w_0)+{\phi }_2(w)(w-w_0),\mathrm{\forall }w\in U_2,\end{array}$$ con ${\phi }_1(z_0)=g^{\prime }(z_0)$ y ${\phi }_2(w_0)=f^{\prime }(w_0)$.

Notemos que para todo $z\in U_1$, $w=g(z)\in U_2$, se tiene que: $$\begin{array}{rl}(f\circ g)(z)& =f(g(z))\\ & =f(g(z_0))+{\phi }_2(g(z))(g(z)-g(z_0))\\ & =(f\circ g)(z_0)+{\phi }_2(g(z)){\phi }_1(z)(z-z_0),\mathrm{\forall }z\in U_1,\end{array}$$ entonces, por la continuidad de ${\phi }_1(z)$ y ${\phi }_2(g(z))$ en $z_0$, tenemos que: $$\begin{array}{rl}\underset{z\to z_0}{lim}\frac{(f\circ g)(z)–(f\circ g)(z_0)}{z-z_0}& =\underset{z\to z_0}{lim}\frac{{\phi }_2(g(z)){\phi }_1(z)(z-z_0)}{z-z_0}\\ & =\underset{z\to z_0}{lim}{\phi }_2(g(z)){\phi }_1(z)\\ & ={\phi }_2(g(z_0)){\phi }_1(z_0)\\ & =f^{\prime }(g(z_0))g^{\prime }(z_0).\end{array}$$ Como $z_0\in U_1$ era arbitrario, entonces es claro que $f\circ g$ es analítica en $U_1$ y su derivada está dada por (16.6).

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 16.7.
Determina la derivada de las siguientes funciones y en caso de ser necesario especifica en dónde es analítica la función.

a) $f(z)=(i{z}^2+3z{)}^5$.

Solución. De acuerdo con la regla de la cadena tenemos que: $$f^{\prime }(z)=5(i{z}^2+3z{)}^4(2iz+3).$$ b) $f(z)={\displaystyle \frac{(z^2+1{)}^4}{z^4}}$.

Solución. Considerando la proposición 16.2(3) y la regla de la cadena tenemos que: $$\begin{array}{rl}{f}^{\prime }(z)& =\frac{4(z^2+1{)}^3(2z)(z^4)–(z^2+1{)}^4(4z^3)}{(z^4{)}^2}\\ & =\frac{4(z^2+1{)}^3(z^2-1)}{z^5}.\end{array}$$ c) $f(z)=(z^3+1{)}^{10}$.

Solución. Por la regla de la cadena tenemos que: $$f^{\prime }(z)=10(z^3+1{)}^9(3z)=30z(z^3+1{)}^9.$$

Otro resultado importante, con el que estamos familiarizados por nuestros cursos de Cálculo, es el de la regla de L’Hôpital. Como consecuencia de la analicidad de funciones complejas, tenemos una versión de esta regla para calcular límites de cocientes que consideren indeterminaciones de la forma $0/0$.

Proposición 16.5. (Regla de L’Hôpital.)
Sean $U\subset \mathbb{C}$ un conjunto abierto y $z_0\in U$. Si $f$ y $g$ son dos funciones analíticas en $z_0$ tales que $f(z_0)=0=g(z_0)$ y $g^{\prime }(z_0)\ne 0$, entonces: $$\underset{z\to z_0}{lim}\frac{f(z)}{g(z)}=\frac{f^{\prime }(z_0)}{g^{\prime }(z_0)}.$$

Demostración. Se deja como ejercicio al lector.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 16.8.
Considera las siguientes funciones y determina los siguientes límites:

a) $\underset{z\to 2+i}{lim}{\displaystyle \frac{f(z)}{g(z)}}$, donde $f(z)=z^2–4z+5$ y $g(z)=z^3-z-10i$.

Solución. Es fácil verificar que $f(2+i)=g(2+i)=0$, por lo que evaluar el límite dado nos lleva a una indeterminación de la forma $0/0$. Dado que $f$ y $g$ son funciones polinómicas, es claro que son funciones enteras, cuyas derivadas son: $$\begin{array}{r}{f}^{\prime }(z)=2z-4,\\ g^{\prime }(z)=3z^2-1\end{array}$$ y $g^{\prime }(i)\ne 0$, por lo que de acuerdo con la regla de L’Hôpital tenemos que: $$\begin{array}{rl}\underset{z\to 2+i}{lim}\frac{f(z)}{g(z)}& =\underset{z\to 2+i}{lim}\frac{z^2-4z+5}{z^3-z-10i}\\ & =\frac{2(2+i)–4}{3(2+i{)}^2-1}\\ & =\frac{2i}{12i+8}\\ & =\frac{3}{26}+\frac{1}{26}i.\end{array}$$ b) $\underset{z\to i}{lim}{\displaystyle \frac{f(z)}{g(z)}}$, donde $f(z)=z^{14}+1$ y $g(z)=z^7+i$.

Solución. Claramente $f(i)=g(i)=0$, por lo que evaluar el límite dado nos lleva a una indeterminación de la forma $0/0$. Dado que $f$ y $g$ son funciones polinómicas, es claro que son funciones enteras con derivadas: $$\begin{array}{r}{f}^{\prime }(z)=14z^{13},\\ g^{\prime }(z)=7z^6\end{array}$$ y $g^{\prime }(i)\ne 0$, por lo que de acuerdo con la proposición 14.5 tenemos que: $$\begin{array}{rl}\underset{z\to i}{lim}\frac{f(z)}{g(z)}& =\underset{z\to i}{lim}\frac{z^{14}+1}{z^7+i}\\ & =\frac{14i^{13}}{7i^6}\\ & =2i^7\\ & =-2i.\end{array}$$

Proposición 16.6. (Teorema de la función inversa.)
Sean $U,G\subset \mathbb{C}$ dos conjuntos abiertos, $f:U\to G$ una función biyectiva, $g:G\to U$ la inversa de $f$ y $z_0\in G$. Si $f$ es analítica en $g(z_0)$ con $f^{\prime }(g(z_0))\ne 0$ y $g$ es continua en $z_0$, entonces $g$ es analítica en $z_0$ y su derivada es: $$g^{\prime }(z_0)=\frac{1}{f^{\prime }(g(z_0))}.$$

Demostración. Dadas las hipótesis, como $f(g(z))=z$ para todo $z\in G$, entonces tenemos que: $$\begin{array}{rl}{g}^{\prime }(z_0)& =\underset{z\to z_0}{lim}\frac{g(z)–g(z_0)}{z–z_0}\\ & =\underset{z\to z_0}{lim}\frac{g(z)–g(z_0)}{f(g(z))–f(g(z_0))}\\ & =\underset{z\to z_0}{lim}{\displaystyle \frac{1}{{\displaystyle \frac{f(g(z))–f(g(z_0))}{g(z)–g(z_0)}}}}.\end{array}$$

Sea $w=g(z)$, definimos: $$\phi (w)=\{\begin{array}{lcc}{\displaystyle \frac{f(w)–f(w_0)}{w–w_0}}& \text{si}& w\ne w_0,\\ f^{\prime }(w_0)& \text{si}& w=w_0.\end{array}$$

Dado que $f$ es analítica en $w_0=g(z_0)$, entonces: $$\begin{array}{rl}\phi (w_0)=f^{\prime }(w_0)& =\underset{w\to w_0}{lim}\frac{f(w)–f(w_0)}{w-w_0}\\ & =\underset{w\to w_0}{lim}\phi (w),\end{array}$$ por lo que $\phi$ es una función continua en $w_0$. Por otra parte, como $g$ es continua en $z_0$, entonces $\underset{z\to z_0}{lim}g(z)=g(z_0)=w_0\in U$. Así, por la proposición 15.4 de la entrada anterior, tenemos que: $$\begin{array}{rl}{g}^{\prime }(z_0)& =\underset{z\to z_0}{lim}\frac{1}{\phi (g(z))}\\ & =\frac{1}{\phi (\underset{z\to z_0}{lim}g(z))}\\ & =\frac{1}{f^{\prime }(w_0)}\\ & =\frac{1}{f^{\prime }(g(z_0))}.\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Definición 16.3. (Singularidad o punto singular.)
Si una función compleja $f$ no es analítica en un punto $z_0\in \mathbb{C}$, pero es analítica en algún punto de cada disco abierto $B(z_0,r)\subset \mathbb{C}$, $r>0$, entonces $z_0$ se llama un punto singular o singularidad de $f$.

Ejemplo 16.9.
De acuerdo con el ejemplo 16.6(b) el punto $z_0=-1+3i$ es un punto singular de la función $f(z)={\displaystyle \frac{(z+1)(z+i{)}^3}{z+1-3i}}$.

Por otra parte, por el el ejemplo 16.3(a) sabemos que la función $f(z)=\bar{z}$ no es analítica en ningún punto de $\mathbb{C}$, por lo que $f$ no tiene puntos singulares.

Tarea moral

1. Mediante la definición 16.1 obtén la derivada de las siguientes funciones.
   a) $f(z)=z–{\displaystyle \frac{1}{z}}$.
   b) $f(z)=-z^{-2}$.
   c) $f(z)={\displaystyle \frac{1}{i2z}}$.
2. Sean $a,b\in \mathbb{C}$ constantes y $n\in {\mathbb{N}}^{+}$. Determina dónde existen las derivadas de las siguientes funciones y utiliza las reglas de diferenciación para obtener sus derivadas.
   a) $f(z)={\displaystyle \frac{1}{(z-a{)}^n}}$.
   b) $f(z)={\displaystyle \frac{i{z}^2-2z}{3z-i+1}}$.
   c) $f(z)={\left({\displaystyle \frac{z-a}{z-b}}\right)}^n$.
   d) $f(z)=z+{\displaystyle \frac{1}{z(z^2-b)}}$.
3. Considera a la función $f:\mathbb{C}\setminus 0\to \mathbb{C}$ dada por $f(z)=z^n$. Prueba que $f$ es analítica en $\mathbb{C}\setminus \{0\}$, para toda $n\in \mathbb{Z}$, y que su derivada está dada por (16.3).
4. Demuestra la proposición 16.5. Hint: Considera que: $$\frac{f(z)}{g(z)}=\frac{f(z)–f(z_0)}{z-z_0}\frac{1}{\frac{g(z)–g(z_0)}{z-z_0}}.$$
5. Considera a la función $f(z)=|z{|}^2$, la cual es continua en el punto $z=0$.
   a) Prueba que $f(z)$ es diferenciable en el origen.
   b) Prueba que $f(z)$ no es diferenciable en nigún punto $z\ne 0$.
6. Calcula los siguientes límites.
   a) $\underset{z\to \sqrt{2}i}{lim}{\displaystyle \frac{z^3+5z^2+2z+10}{z^5+2z^3}}$.
   b) $\underset{z\to 1+i}{lim}{\displaystyle \frac{z^5+4z}{z^2-2z+2}}$.
   c) $\underset{z\to \sqrt{2}(1+i)}{lim}{\displaystyle \frac{z^4+16}{z^2-2\sqrt{2}z+4}}$.
   Hint: Utiliza la regla de L’Hôpital.
7. Prueba que la función $f(z)=|z|$ no es diferenciable en ningún punto.

Más adelante…

Como hemos visto con los ejemplos anteriores, las reglas de diferenciación, en el sentido complejo, para la suma, el producto y el cociente de funciones, al igual que para las potencias enteras, parecen ser simplemente una extensión de las reglas de diferenciación para funciones reales, sin embargo como hemos mencionado antes, la derivada en el caso complejo es más restrictiva. A pesar de que parezca que simplemente estamos trabajando con la variable $z$, no debemos olvidar que dicha variable depende a su vez de dos variables, su parte real y su parte imaginaria, por lo que las reglas de diferenciación obtenidas hasta ahora puede que no nos permitan obtener la derivada de algunas funciones complejas, incluso aunque estas funciones sí posean derivadas, por ejemplo si consideramos a las funciones $f(z)=4x^2–iy$ y $g(z)=xy+i(x+y)$, es claro que no podemos utilizar la proposición 16.2 para intentar obtener sus derivadas, en caso de existir.

Es importante remarcar que a diferencia del caso real en el que dabamos distintas interpretaciones a la derivada de una función, en el caso complejo no nos centraremos en darle una interpretación a la derivada, sino que nos enfocaremos en saber si una función compleja tiene o no derivada, ya que la existencia de la misma nos dice mucho sobre la función compleja. Por ello en la siguiente entrada caracterizaremos la diferenciabilidad compleja mediante las ecuaciones de Cauchy-Riemann, las cuales resultan ser una condición necesaria para asegurar la diferenciabilidad de una función compleja y veremos que bajo ciertas condiciones podemos garantizar que también son una condición suficiente.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Continuidad en $\mathbb{C}$.
• Siguiente entrada del curso: Ecuaciones de Cauchy-Riemann. Condiciones necesarias para la diferenciabilidad compleja.