Introducción
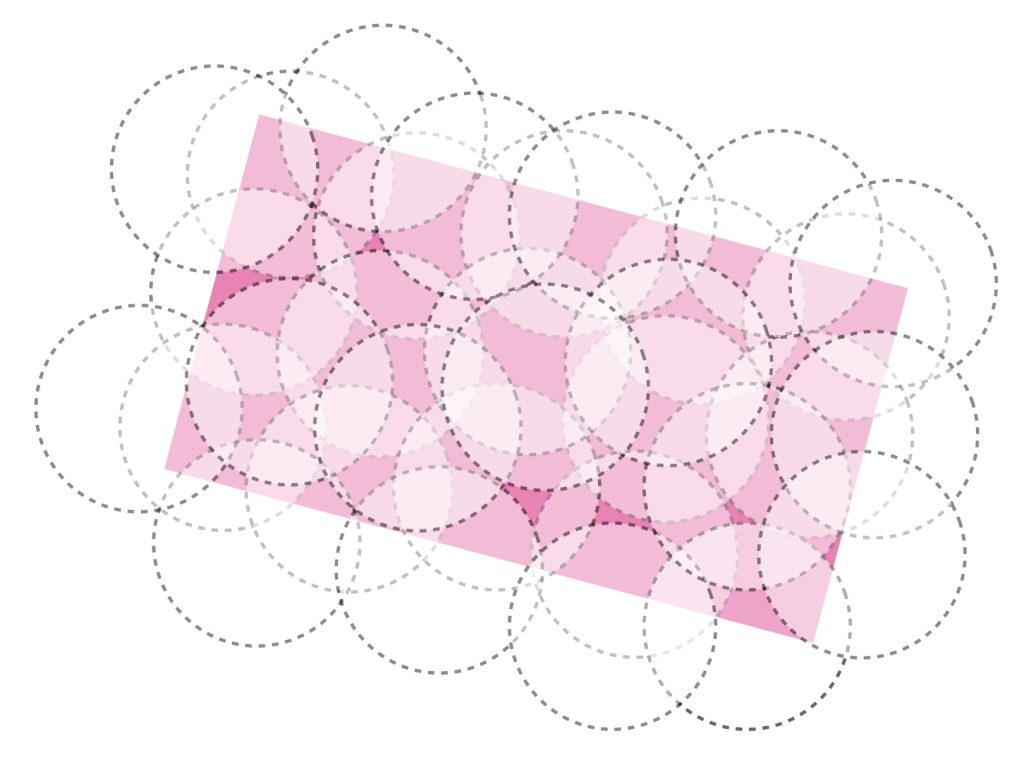
En la sección La métrica de Hausdorff definimos que un conjunto acotado es aquel que está contenido en una bola del espacio métrico. Hay una propiedad más específica de los, así llamados, conjuntos totalmente acotados. Consiste en encerrar al conjunto en una unión de bolas abiertas tan pequeñas como se desee. La particularidad radica en que, por muy pequeño que sea el radio de estas bolas, bastará con una cantidad finita de ellas para cubrir todo el conjunto. Formalmente esta idea se expresa como:
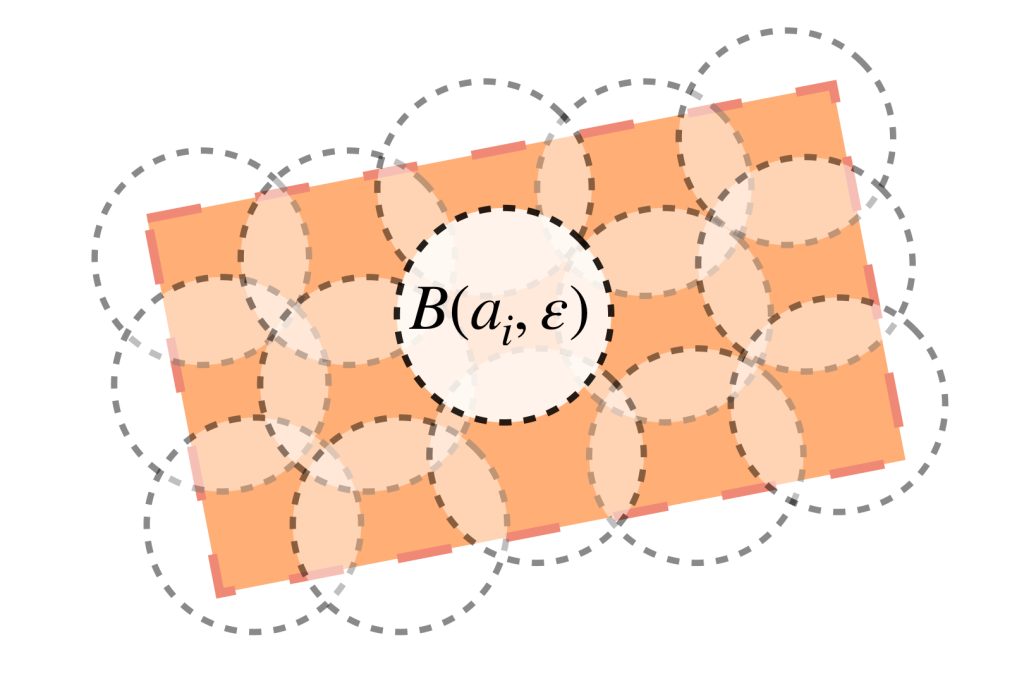
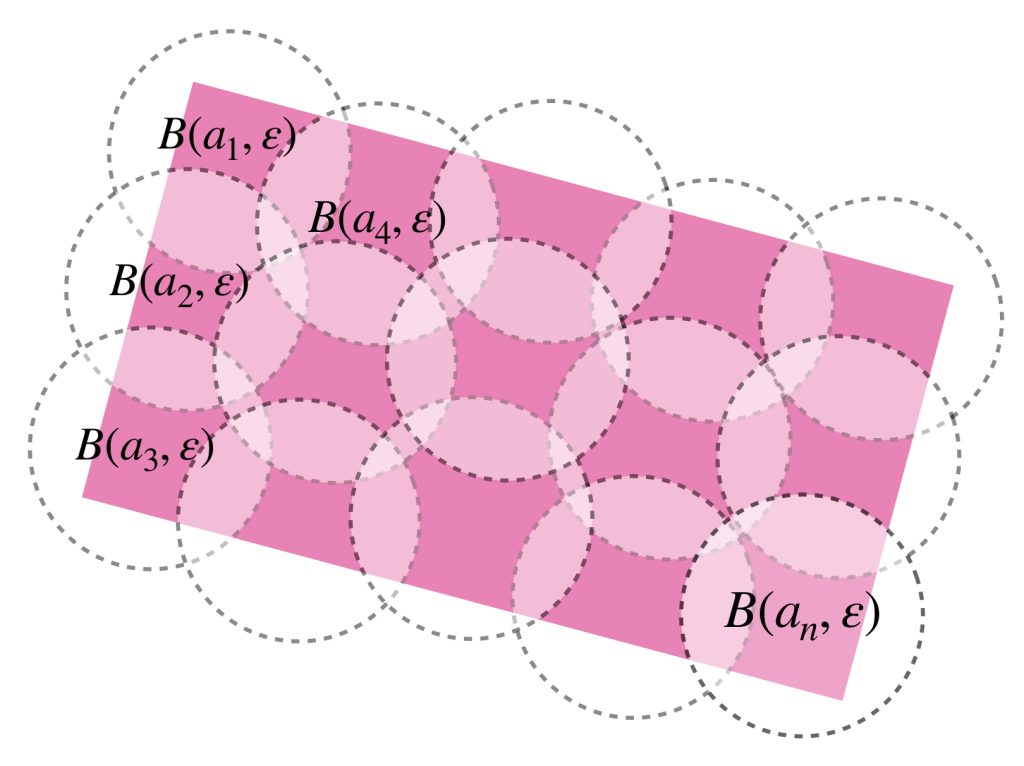
Definición. Conjunto totalmente acotado. Sea $(X,d)$ un espacio métrico y $A \subset X.$ Si para todo $\varepsilon >0$ existe una cantidad finita de puntos $a_1,…,a_n \in A$ tales que
$$A \subset \underset{i =1,…,n}{\bigcup}\, B(a_i,\varepsilon)$$
diremos que $A$ es totalmente acotado.
Por supuesto que esta propiedad asegura que el conjunto sea acotado.
Proposición. Si $A \subset X$ es totalmente acotado, entonces $A$ es acotado.
Demostración:
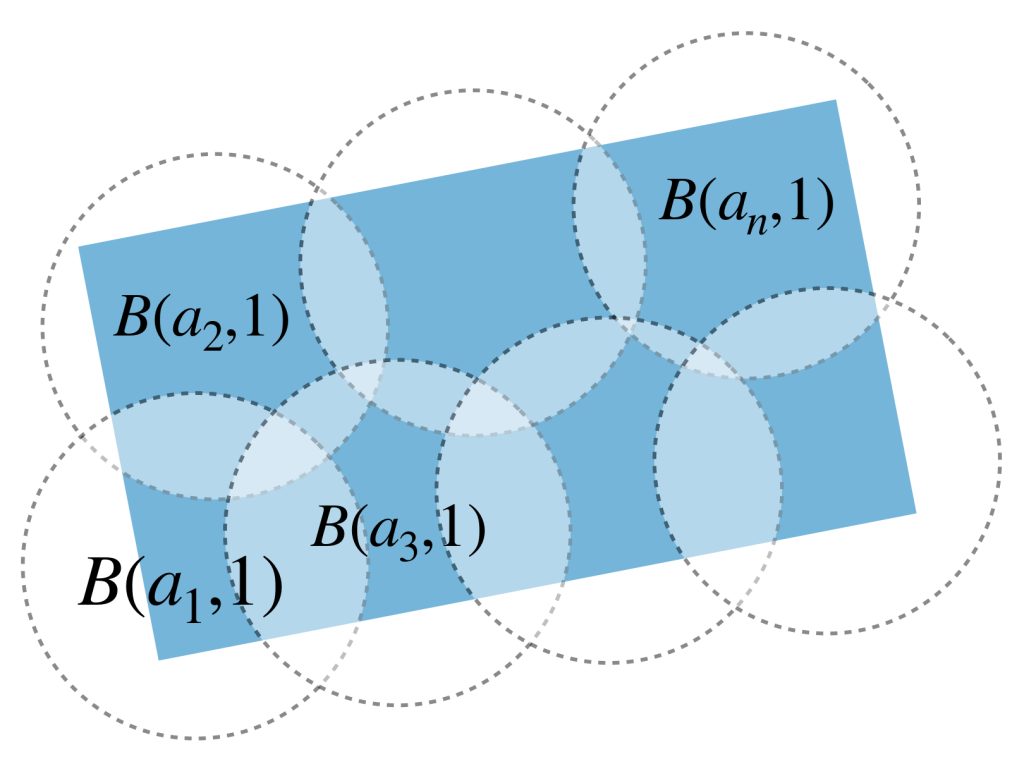
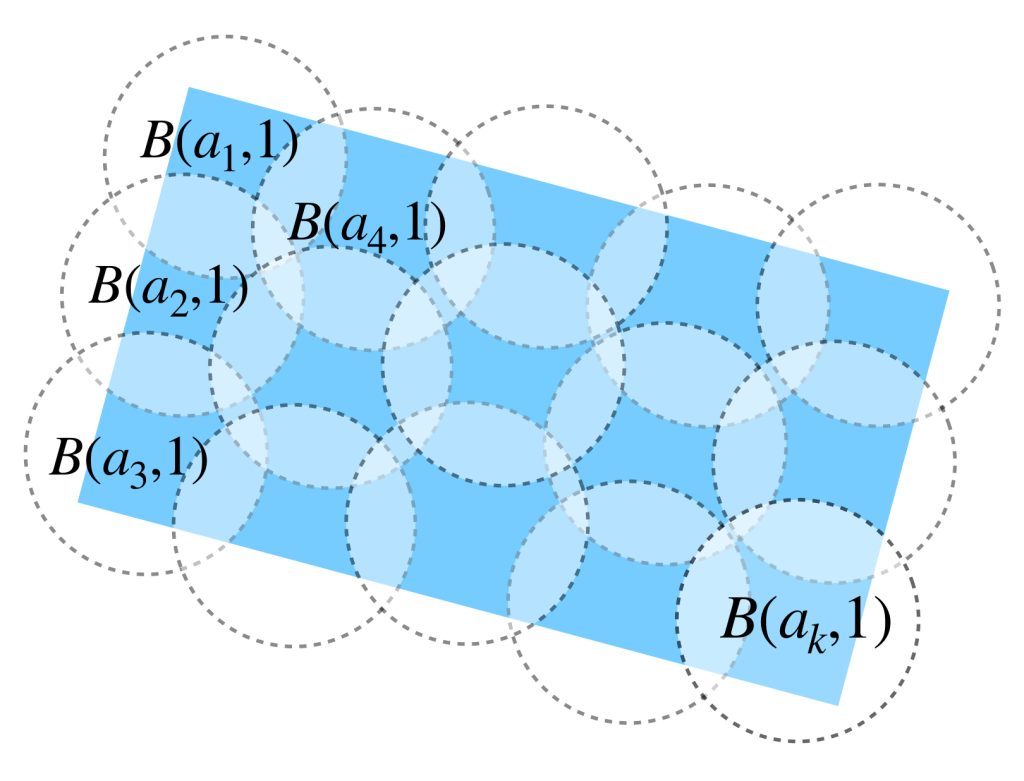
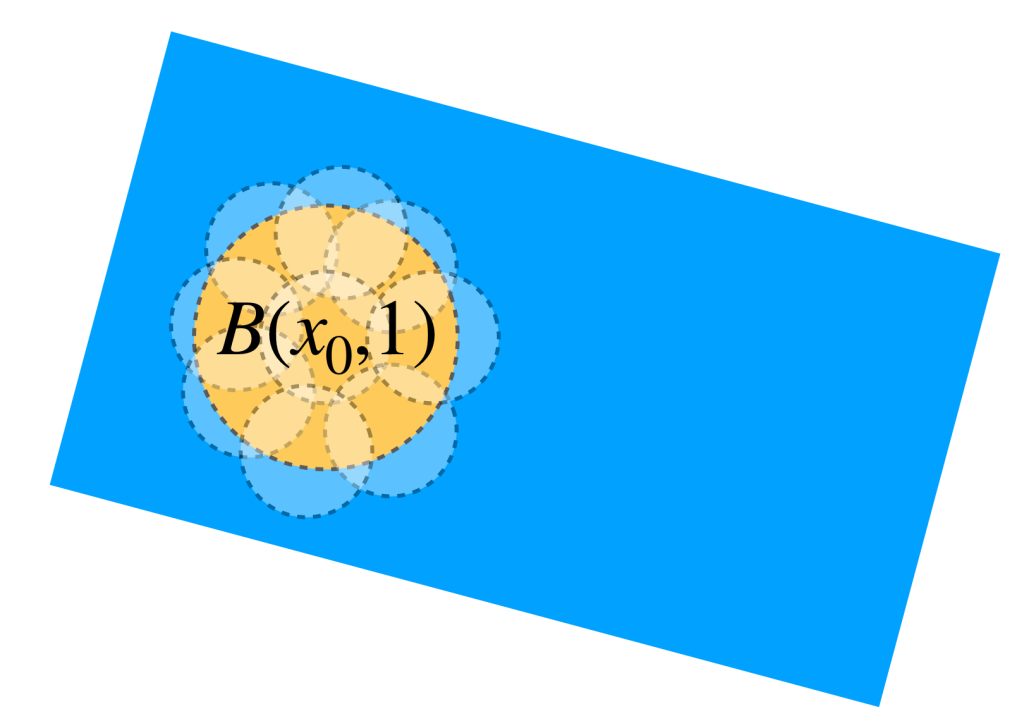
Como $A$ es totalmente acotado, existen $a_1,a_2,…,a_n \in A$ tales que $A \subset \underset{i =1,…,n}{\bigcup}B(a_i,1).$ Ahora busquemos una bola abierta en $X$ que contenga al conjunto $A.$
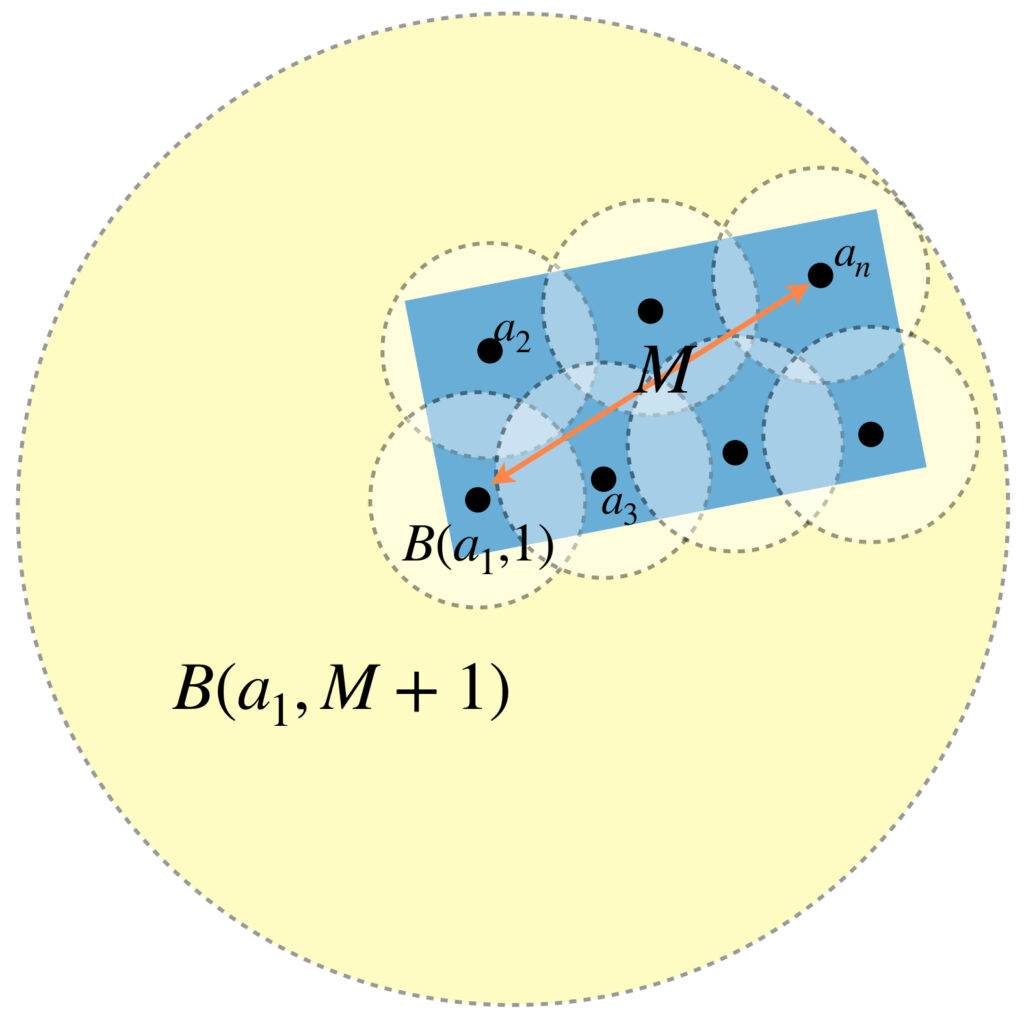
Considera la máxima distancia entre $a_1$ y el resto de los centros. Llamémosla $M$ es decir, $M = max\{d(a_1,a_k) \, | \, k=2,…,n\}.$ A continuación identificaremos una bola abierta con centro en $a_1$ que cumplirá lo deseado.
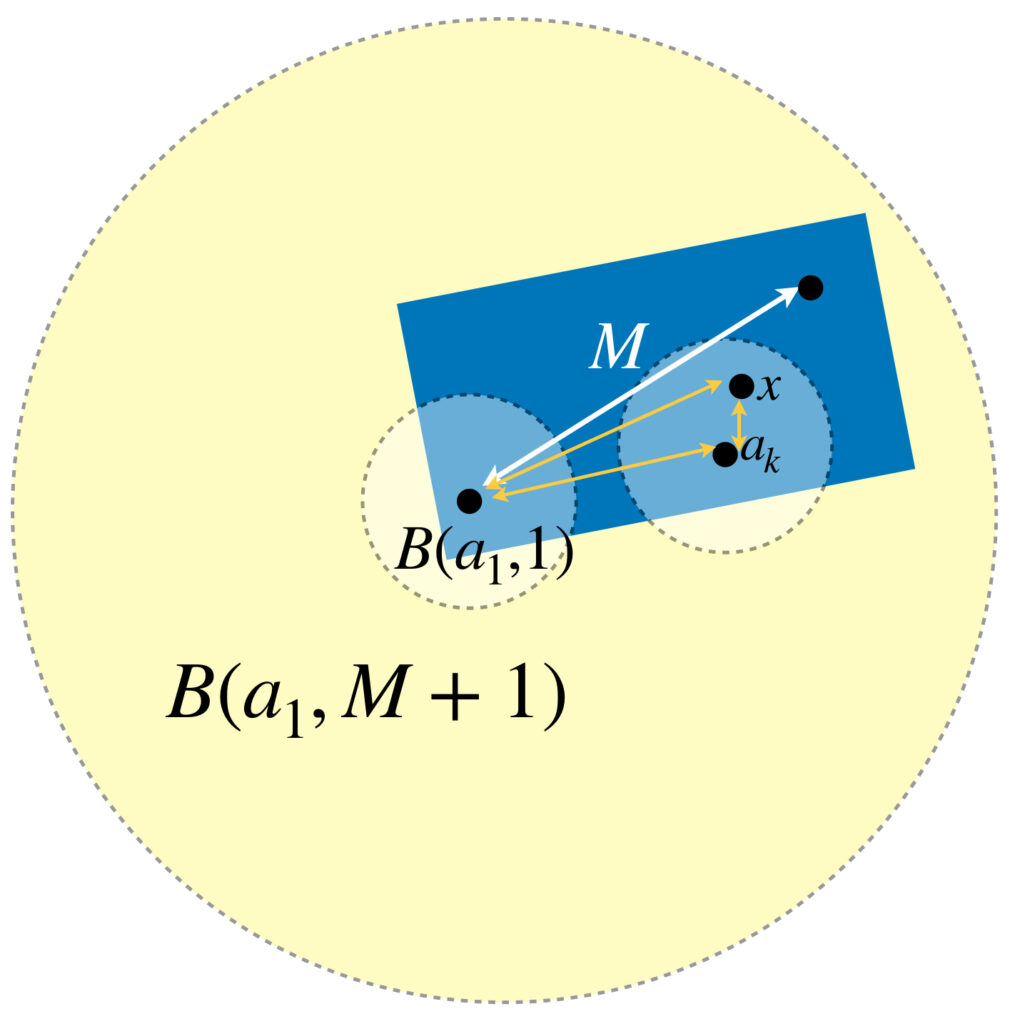
Si $x \in A$ se tiene que $x \in B(a_k,1)$ para algún $k \in \{1,…,n\},$ así:
\begin{align*}
d(a_1,x)&\leq d(a_1,a_k) + d(a_k,x) \\
&< M + 1
\end{align*}
Por lo tanto $A \subset B(a_1,M+1),$ concluyendo así que $A$ es acotado.
Contrario a lo anterior, en general no es cierto que todo conjunto acotado sea totalmente acotado:
Contraejemplo: Considera el espacio de las sucesiones en $\mathbb{R}$ dado por $l_1 =\{(x_n)_{n \in \mathbb{N}} \, | \, \sum_{n=1}^{\infty} |x_n| < \infty \}$ con la norma definida como $\norm{(x_n)}_1 := \sum_{n=1}^{\infty}|x_n|.$
Sea $A=\{e_i \, | \, i \in \mathbb{N}\}$ donde $e_i$ es la sucesión que toma a $1$ como valor en la entrada $i$ y $0$ en el resto.
Este conjunto es acotado en $l_1$ pues para cada $i \in \mathbb{N}, \, \norm{e_i}_1= \sum_{n=1}^{\infty}|x_n|= |1|=1$ de modo que $A \subset B(\mathcal{0},2)$ donde $\mathcal{0}$ es la sucesión constante cero.
No obstante, $A$ no es totalmente acotado. Si calculamos la distancia entre dos sucesiones en $A$ tenemos que para cualesquiera $i \neq j, \, d(e_i,e_j)= |1|+|1|= 2.$ Por lo tanto si se elige $\varepsilon >0,$ tal que $\varepsilon \leq 2$ cada bola de radio $\varepsilon$ con centro en alguna sucesión de $A$ excluye al resto de los elementos de $A$, de modo que no será posible cubrir $A$ con una cantidad finita de bolas de radio $\varepsilon$ cuyo centro esté en $A.$
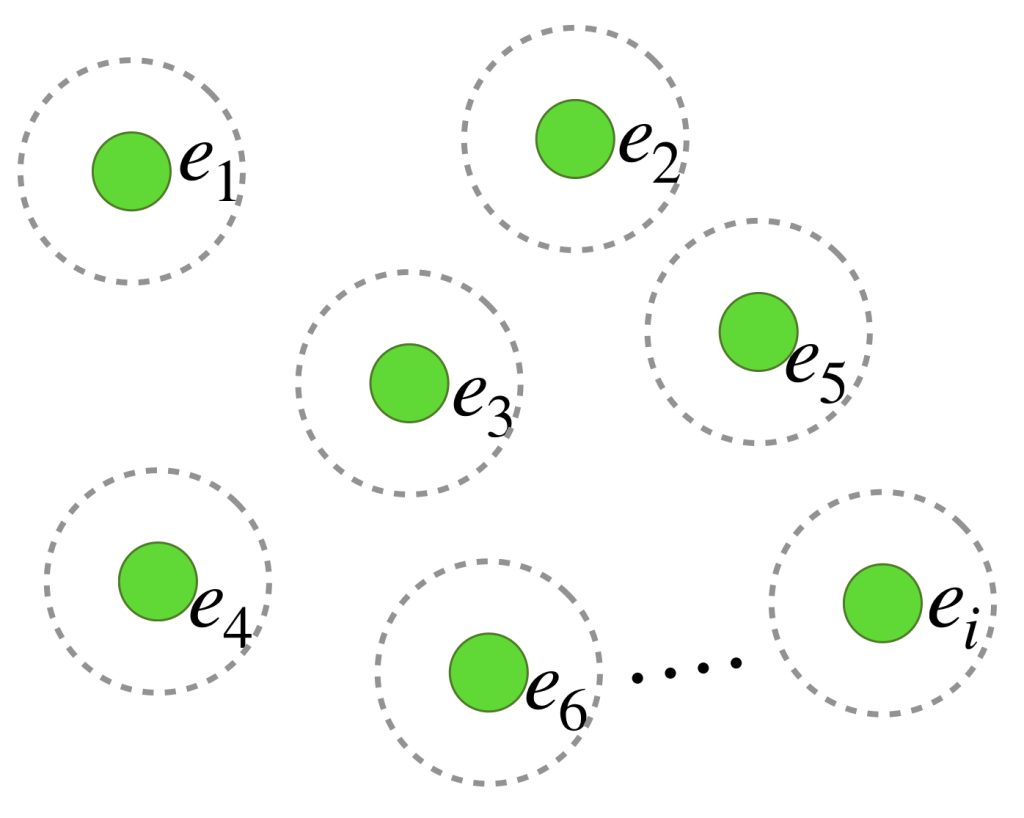
Esto nos permite concluir que $A$ no es totalmente acotado.
El ejemplo nos incentiva algunas preguntas: ¿Es el conjunto $A$ cerrado en $l_1?$ ¿Es compacto? ¿Bastará con que un conjunto sea totalmente acotado para que sea compacto? Al final de esta sección podrás responderlas.
Por lo pronto veamos que la propiedad de ser totalmente acotado, se hereda en subconjuntos:
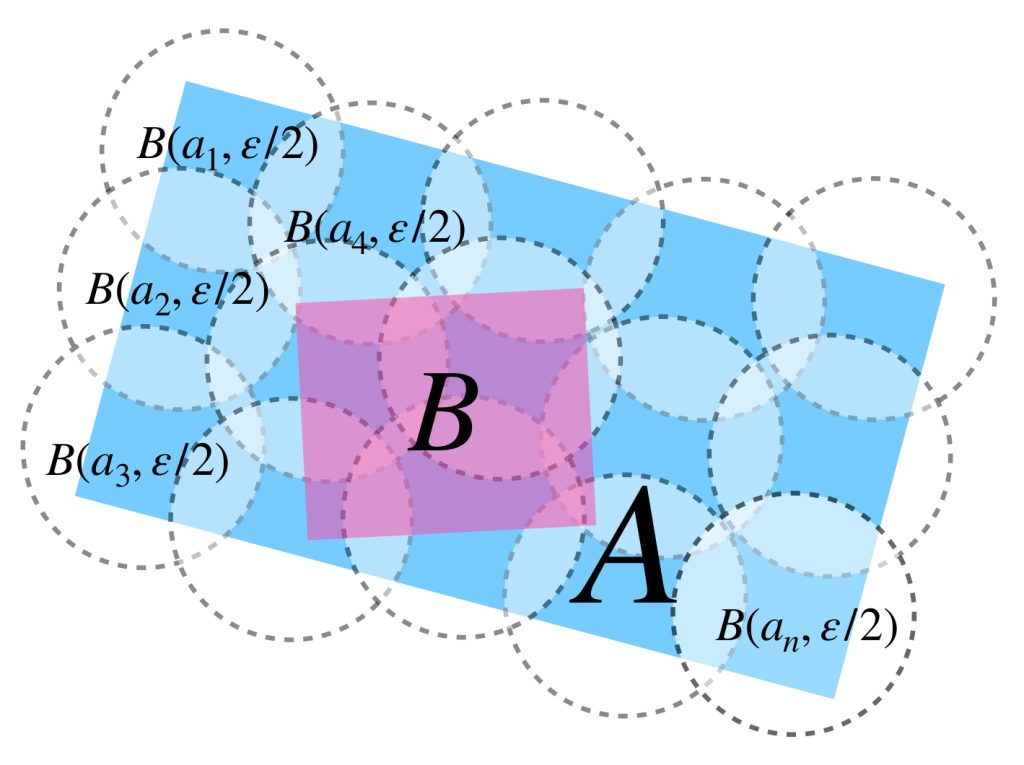
Proposición. Sea $A \subset X$ un conjunto totalmente acotado. Si $B \subset A$ entonces $B$ es totalmente acotado.
Demostración:
Sea $\varepsilon >0.$ Como $A$ es totalmente acotado, existen puntos $a_1,…,a_n \in A$ tales que:
$$B \subset A \subset \underset{i =1,…,n}{\bigcup}\, B(a_i,\frac{\varepsilon}{2})$$
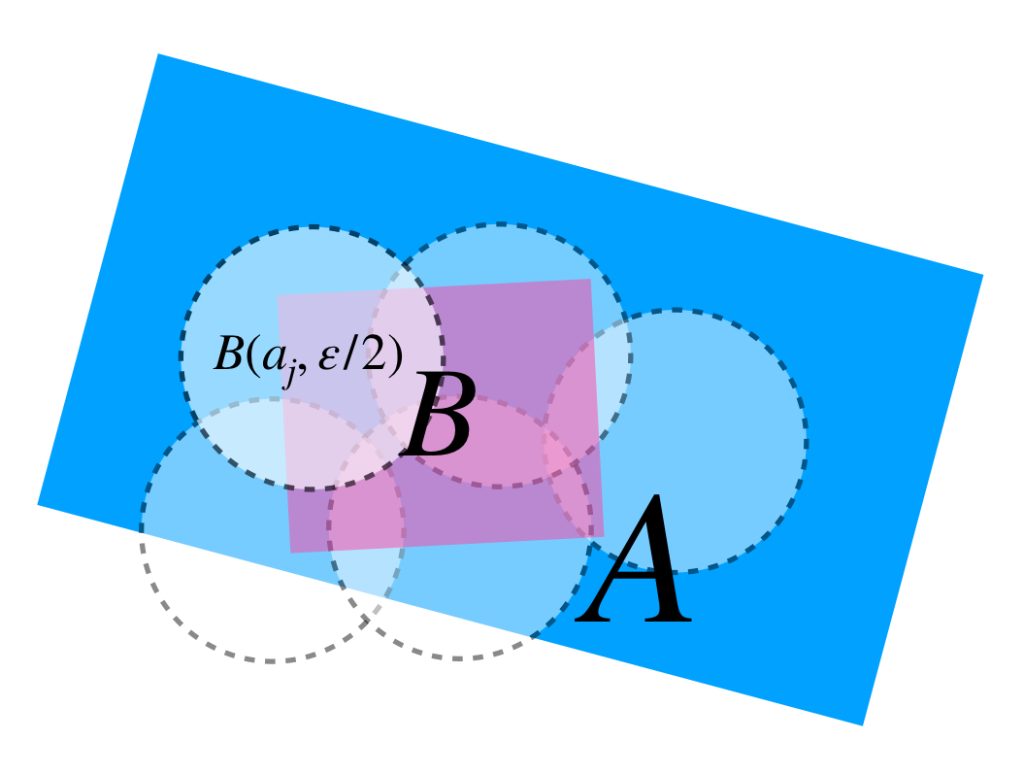
Consideremos únicamente a las bolas abiertas que tienen elementos de $B.$ Sea $\mathcal{J}:= \{j \in \{1,…,n\} \, | \, B(a_j, \frac{\varepsilon}{2}) \cap B \neq \emptyset\}$En efecto, $B \subset \underset{j \in \mathcal{J}}{\bigcup}\, B(a_j,\frac{\varepsilon}{2}).$
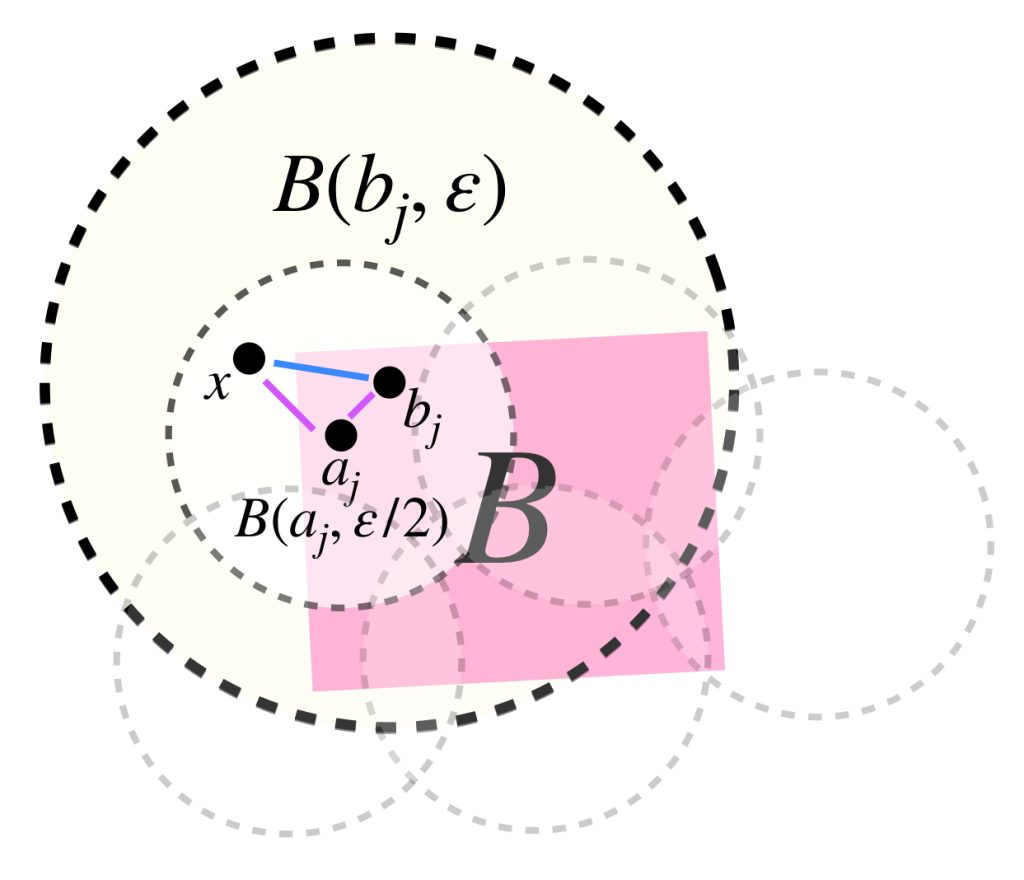
Para cada $j \in \mathcal{J},$ sea $b_j \in B(a_j,\frac{\varepsilon}{2}) \cap B.$ Nota que dicha bola está contenida en $B(b_j,\varepsilon)$ por lo siguiente:
Si $x \in B(a_j,\frac{\varepsilon}{2})$ entonces $d(x,b_j) \leq d(x,a_j) + d(a_j,b_j) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2} = \varepsilon.$
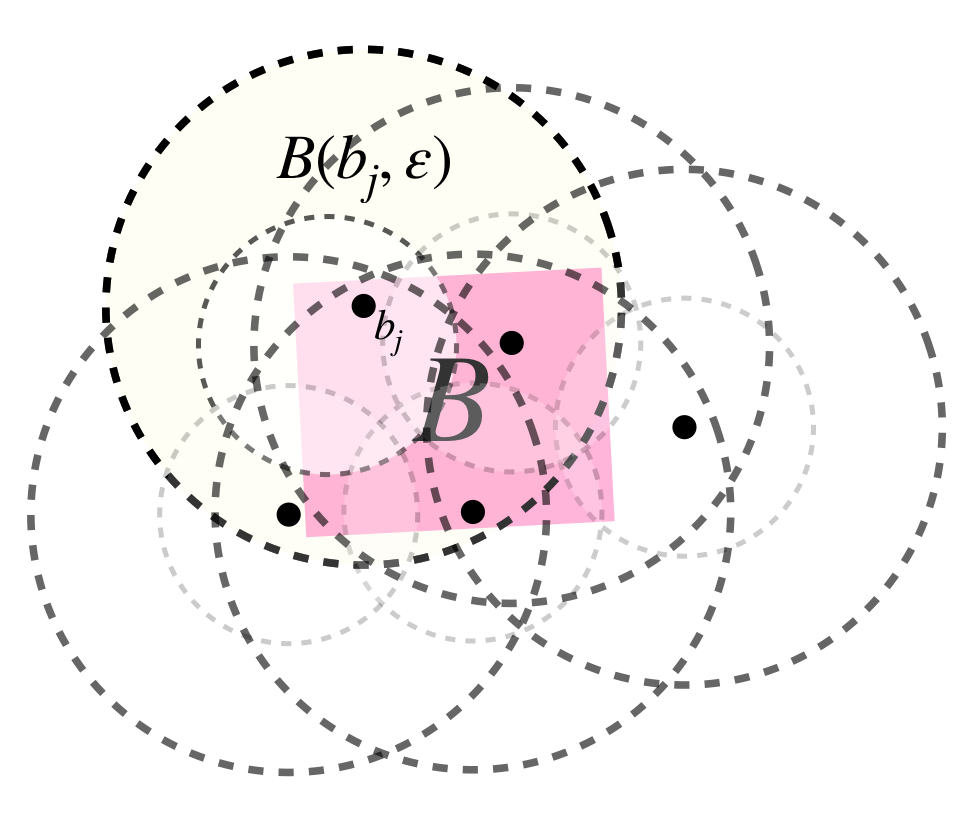
Por lo tanto para cada $j \in \mathcal{J}, \, B(a_j,\frac{\varepsilon}{2}) \subset B(b_j,\varepsilon),$ de modo que $B \subset \underset{j \in \mathcal{J}}{\bigcup}\, B(a_j,\frac{\varepsilon}{2}) \subset \underset{j \in \mathcal{J}}{\bigcup}\, B(b_j,\varepsilon)$ lo que nos permite concluir que $B$ es totalmente acotado.
Proposición. Si $A \subset X$ es totalmente acotado entonces $\overline{A}$ también es totalmente acotado. La demostración se deja como ejercicio.
Proposición. Si $A \subset X$ es compacto entonces $A$ es totalmente acotado.
Demostración:
Sea $\varepsilon >0$ y $A$ un conjunto compacto. Para cada punto $a \in A$ considera $B(a,\varepsilon).$ Entonces el conjunto $\{B(a,\varepsilon) \, | \, a \in A\}$ es una cubierta abierta de $A.$
Como $A$ es compacto entonces existe una subcubierta finita $\{B(a_1,\varepsilon),B(a_2,\varepsilon),…,B(a_n,\varepsilon)\}.$ Por lo tanto, $A$ es totalmente acotado.
En general no es cierto que un conjunto totalmente acotado sea compacto. El regreso requiere de una propiedad más:
Proposición. $A \subset X$ es compacto si y solo si es completo y totalmente acotado.
Demostración:
Supón que $A$ es un conjunto compacto. Ya vimos que esto lo hace totalmente acotado, ahora comprobemos que también es completo. Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy en $A.$ Por lo visto en la entrada de Compacidad en espacios métricos sabemos que $(x_n)$ tiene una subsucesión que converge en $A.$ Luego, por la entrada Sucesiones de Cauchy sabemos que esto permite concluir que $(x_n)$ es convergente, por lo tanto $A$ es completo.
En el regreso partimos de que $A$ es completo y totalmente acotado. Supongamos por el contrario que $A$ no es compacto. Entonces existe una cubierta abierta $\mathcal{C} = \{ A_i \, | \, i \in \mathcal{I} \}$ de $A$ tal que no tiene subcubierta finita.
Como $A$ es totalmente acotado, entonces está contenido en una unión finita de bolas de radio $1$
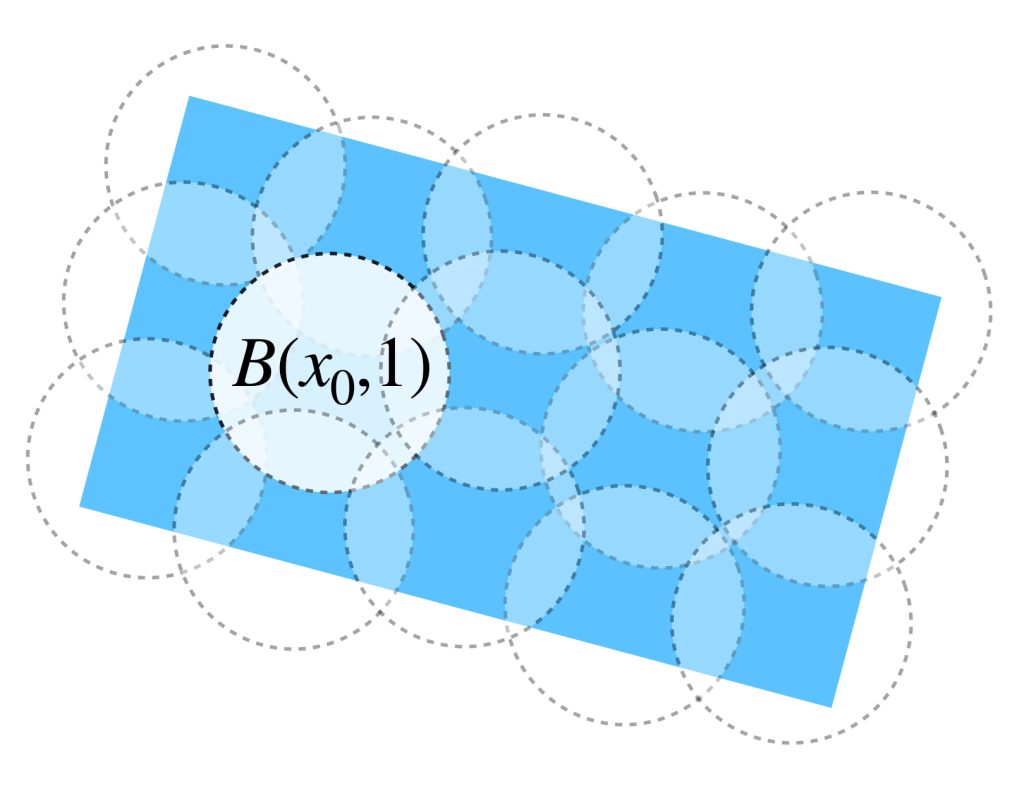
Al menos una de esas bolas no puede ser cubierta por una unión finita de elementos de $\mathcal{C}$ pues si todas las bolas pudieran ser cubiertas de esa forma, entonces sí tendríamos una subcubierta finita de $\mathcal{C}$ para $A.$
Sea $B(x_0,1)$ esa bola. Como está contenida en la bola cerrada $\overline{B}(x_0,1)$, que es compacta y, en consecuencia, totalmente acotada, se sigue que $B(x_0,1)$ también es totalmente acotada. Por lo tanto, está cubierta por un número finito de bolas abiertas de radio $\frac{1}{2}.$
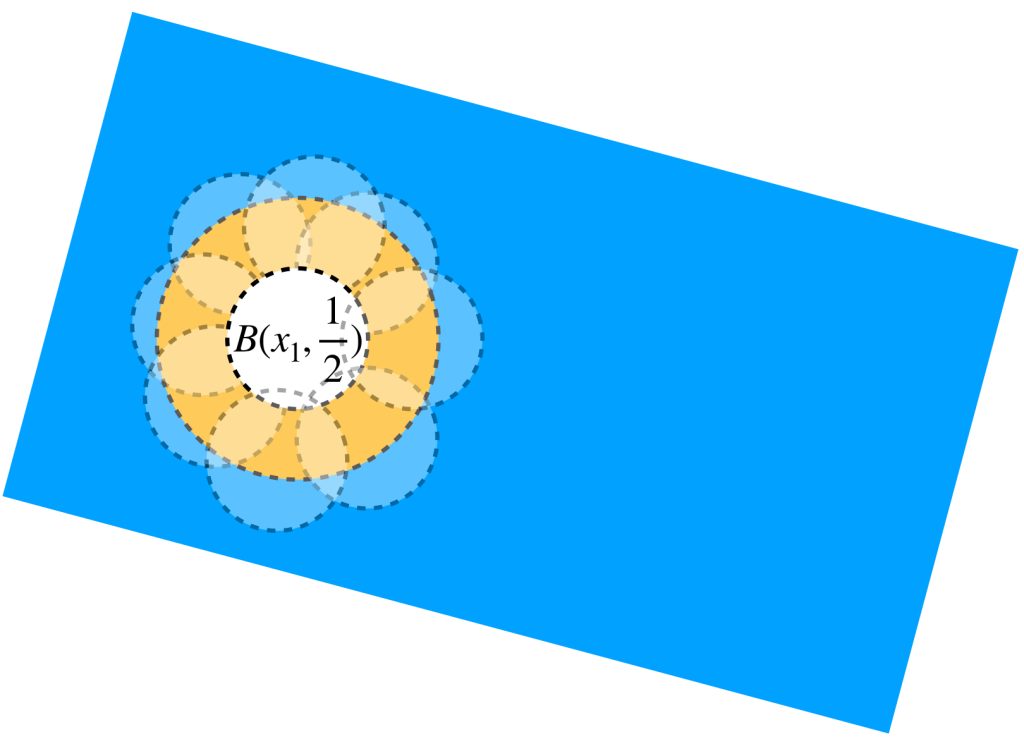
Por el argumento arriba mencionado, existe una bola $B(x_1,\frac{1}{2})$ que no puede ser cubierto por una cantidad finita de elementos de $\mathcal{C}.$
Continuando con este procedimiento, podemos construir una sucesión $(x_n)_{n \in \mathbb{N}} \,$ donde para cada $n \in \mathbb{N}, \, x_n$ es el centro de una bola de radio $\frac{1}{n+1}$ que no puede ser cubierta por una cantidad finita de elementos de $\mathcal{C}$ y $x_n$ está en la bola abierta $B(x_{n-1},\frac{1}{n}).$
Queda como ejercicio al lector demostrar que la sucesión $(x_n)$ es de Cauchy. Como $A$ es completo, se sigue que $x_n \to x^*$ para algún $x^* \in A.$
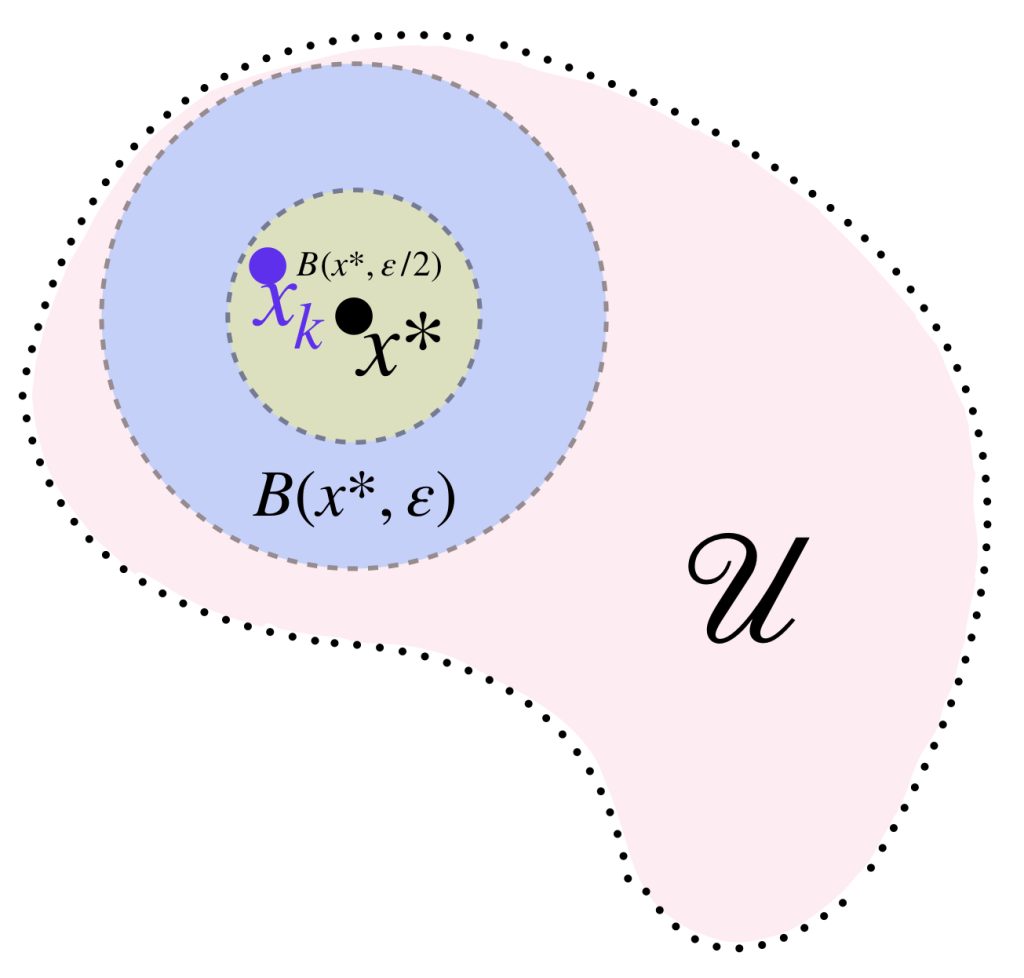
Sea $\mathcal{U} \in \mathcal{C}$ tal que $x^* \in \mathcal{U}.$ Como $\mathcal{U}$ es abierto, existe $\varepsilon >0$ tal que $B(x^*,\varepsilon) \subset \mathcal{U}.$ Como $x_n \to x^*$ existe $N \in \mathbb{N}$ tal que para cada $ \, k \geq N, d(x_k, x^*)< \frac{\varepsilon}{2}.$
Sea $K \in \mathbb{N}$ tal que $K > N$ y además, $\frac{1}{K} < \frac{\varepsilon}{2}.$ Demostraremos que $B(x_{K-1}, \frac{1}{K}) \subset \mathcal{U}.$
Si $x \in B(x_{K-1}, \frac{1}{K})$ se sigue que:
\begin{align*}
d(x,x^*) &\leq d(x,x_{K-1}) + d(x_{K-1},x^*) \\
&< \frac{1}{K} + \frac{\varepsilon}{2} \\
&< \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \\
&= \varepsilon
\end{align*}
En consecuencia $B(x_{K-1}, \frac{1}{K}) \subset \mathcal{U}$ lo cual es una contradicción, pues habíamos dicho que no puede ser cubierto por una cantidad finita de elementos de $\mathcal{C}.$ Por lo tanto $A$ es un conjunto compacto.
Hemos visto que si un conjunto no es cerrado tampoco es compacto. No obstante puede ocurrir que la cerradura del conjunto sí lo sea. Tenemos la siguiente:
Definición. Conjunto relativamente compacto. Sea $(X,d)$ espacio métrico y sea $A \subset X.$ Diremos que $A$ es relativamente compacto si $\overline{A}$ es compacto.
Proposición. Sea $(X,d)$ un espacio métrico completo. Entonces $A \subset X$ es relativamente compacto en $X$ si y solo si es totalmente acotado.
Demostración:
Si $A$ es relativamente compacto entonces $\overline{A}$ es compacta en $X$ y por tanto, totalmente acotado. Como $A \subset \overline{A}$ concluimos por una proposición vista arriba que $A$ también es totalmente acotado.
Por otro lado, partiendo de que $A$ es totalmente acotado tenemos por la proposición que dejamos como ejercicio, que $\overline{A}$ también es totalmente acotado. Además, $\overline{A}$ es completo, pues es un subconjunto cerrado en $X$ completo, (ver Espacios métricos completos) así podemos concluir por la proposición de arriba, que $\overline{A}$ es compacto.
Más adelante…
Usaremos los términos vistos en esta entrada y sus equivalencias para enunciar y demostrar el teorema de Arzelá-Ascoli.
Tarea moral
- Considera el espacio de las sucesiones en $\mathbb{R}$ dado por $l_1 =\{(x_n)_{n \in \mathbb{N}} \, | \, \sum_{n=1}^{\infty} |x_n| < \infty \}$ donde la norma se define como $\norm{(x_n)}_1 := \sum_{n=1}^{\infty}|x_n|.$ Sea $A=\{e_i \, | \, i \in \mathbb{N}\}$ donde $e_i$ es la sucesión que toma a $1$ como valor en la entrada $i$ y $0$ en el resto. ¿Es el conjunto $A$ cerrado en $l_1?$ ¿Es compacto?
- Da un ejemplo de un conjunto totalmente acotado que no sea compacto.
- Demuestra que si $A$ es totalmente acotado entonces $\overline{A}$ también es totalmente acotado.
- Demuestra que la sucesión $(x_n)_{n \in \mathbb{N}} \,$ de la demostración de $»A \subset X$ es compacto si y solo si es completo y totalmente acotado«, es de Cauchy.
- Sea $X$ un espacio métrico. Demuestra que si toda sucesión en $X$ tiene una subsucesión que converge en $X$ entonces es completo y totalmente acotado. Nota que es lo que falta para concluir que son equivalentes:
a) $X$ es compacto.
b) Toda sucesión en $X$ tiene una subsucesión que converge en $X.$
c) $X$ es completo y totalmente acotado.