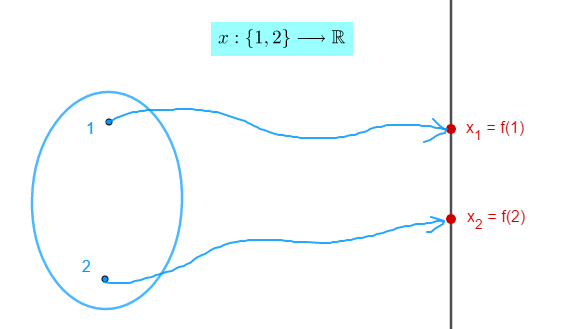
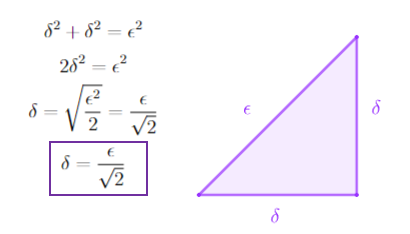Recordemos, en $\mathbb{R}$, sea $\{x_n\}_{n \in \mathbb{N}}$ una sucesión de números reales, es decir una función $$x : \mathbb{N} \longrightarrow \mathbb{R}.$$
Notación: $$x (1) = x_1$$ $$x (2) = x_2$$ $$x (3) = x_3$$ $$\vdots$$
Geométricamente, puntos en la recta $\mathbb{R}$.
Ejemplo: sucesión $\big\{ \frac{1}{n} \big\}$ para $n \in \mathbb{N}$.
https://www.geogebra.org/m/gwet39b2
En $\mathbb{R}^2$; una sucesión de puntos en $\mathbb{R}^2$ es una función $$\vec{x} : \mathbb{N} \longrightarrow \mathbb{R}^2$$
Notación: $$\vec{x}(1) = \overrightarrow{x_1} = (x_1, y_1)$$ $$\vec{x}(2) = \overrightarrow{x_2} = (x_2, y_2)$$ $$\vec{x}(3) = \overrightarrow{x_3} = (x_3, y_3)$$ $$\vdots$$
Geométricamente, vectores en el plano.
https://www.geogebra.org/classic/jyzgsg63
Decimos que un número $L \in \mathbb{R}$ es el límite de la sucesión $\{x_n\}_{n \, \in \mathbb{N}}$, si $\forall \epsilon > 0, \exists N \in \mathbb{N}$ tal que para toda $n > N$ se cumple que $\big|x_n – L \big| < \epsilon$.
Decimos que $\overrightarrow{L} \in \mathbb{R}^2$ es el límite de la sucesión $\Big\{\overrightarrow{x_n}\Big\}_{n \, \in \mathbb{N}}$, si $\forall \epsilon > 0, \exists N \in \mathbb{N}$ tal que $\forall n > N$ se cumple que $\Big\| \overrightarrow{x_n} – \overrightarrow{L} \Big\| < \epsilon.$
Teorema: Si una sucesión tiene dos límites $\overrightarrow{L_1}$ y $\overrightarrow{L_2}$ entonces $\overrightarrow{L_1} = \overrightarrow{L_2}.$
Demostración:
Sea $\Big\{\overrightarrow{x_n} \Big\}_{n \in \mathbb{N}}$ una sucesión en $\mathbb{R}^2$ supongamos que tiene dos límites $\overrightarrow{L_1} \neq \overrightarrow{L_2}.$
Sea $\epsilon_0 = \frac{\overrightarrow{L_1}-\overrightarrow{L_2}}{2}$.
Como $\overrightarrow{L_1}$ es límite entonces a partir de un momento $N_1$ todos los $\overrightarrow{x_n} \in B_{\epsilon_0} \Big( \overrightarrow{L_1} \Big).$
De igual modo, $\overrightarrow{L_2}$ es límite entonces a partir de un momento $N_2$ todos los $\overrightarrow{x_n} \in B_{\epsilon_0} \Big( \overrightarrow{L_2} \Big).$ (CONTRADICCIÓN) ya que todas las bolas son ajenas.
$$\therefore \; \overrightarrow{L_1} = \overrightarrow{L_2} \; _{\blacksquare}$$
Teorema: Sea $\Big\{ \Big( \overrightarrow{x_n}, \overrightarrow{y_n} \Big) \Big\}_{n\, \in \mathbb{N}}$ una sucesión de puntos en $\mathbb{R}^2$. Esta sucesión converge a un punto $\Big( \overrightarrow{L}, \overrightarrow{M} \Big)$ si y sólo si los límites de las coordenadas convergen. Es decir, $$\Big\{\overrightarrow{x_n} \Big\}_{n\, \in \mathbb{N}} \longrightarrow \overrightarrow{L}$$ $$\Big\{\overrightarrow{y_n} \Big\}_{n\, \in \mathbb{N}} \longrightarrow \overrightarrow{M}$$
Demostración:
[$\Rightarrow$] Si $\Big(\overrightarrow{x_n}, \overrightarrow{y_n} \Big) \longrightarrow \Big(\overrightarrow{L}, \overrightarrow{M} \Big)$ entonces $$\overrightarrow{x_n} \longrightarrow \overrightarrow{L}$$ $$\overrightarrow{y_n} \longrightarrow \overrightarrow{M}$$
$\big[$ por demostrar: $\big\{\overrightarrow{x_n}\big\} \longrightarrow \overrightarrow{L} \; \big]$
Sea $\epsilon > 0.$
$\exists \, N > 0$ tal que $n \geq N \Rightarrow \Big|\overrightarrow{x_n} – \overrightarrow{L} \Big| < \epsilon$.
Como $\Big\{ \Big(\overrightarrow{x_n}, \overrightarrow{y_n} \Big) \Big\} \longrightarrow \Big(\overrightarrow{L}, \overrightarrow{M} \Big)$ para $\epsilon > 0$ dada existe $n \geq Ñ \Rightarrow \Big\| \Big(\overrightarrow{x_n}, \overrightarrow{y_n} \Big) \, – \, \Big( \overrightarrow{L}, \overrightarrow{M} \Big) \Big\| < \epsilon$ entonces $$\sqrt{ \Big( \overrightarrow{x_n} – \overrightarrow{L} \Big)^2 + \Big( \overrightarrow{y_n} – \overrightarrow{M} \Big)^2 \, } < \epsilon$$ $$\Big| \overrightarrow{x_n} \, – \, \overrightarrow{L} \Big| \leq \sqrt{\Big(\overrightarrow{x_n} \, – \, \overrightarrow{L} \Big)^2+ \Big(\overrightarrow{y_n} \, – \, \overrightarrow{M}\Big)^2 \, } < \epsilon$$ $$\Rightarrow \Big|\overrightarrow{x_n} \, – \, \overrightarrow{L} \Big| < \epsilon$$
Entonces $N =$ Ñ sirve.
Análogamente la sucesión de $\Big\{\overrightarrow{y_n} \Big\}_{n \, \in \mathbb{N}} \longrightarrow \overrightarrow{M}$.
[$\Leftarrow$] Si las sucesiones $\Big\{\overrightarrow{x_n} \Big\} \Longrightarrow \overrightarrow{L}$ y $\Big\{\overrightarrow{y_n}\Big\} \Longrightarrow \overrightarrow{M}$ entonces la sucesión $\Big\{ \Big(\overrightarrow{x_n}, \overrightarrow{y_n} \Big) \Big\}_{n\, \in \mathbb{N}} \longrightarrow \Big(\overrightarrow{L}, \overrightarrow{M} \Big)$.
Sea $\epsilon > 0$
$\big[$ por demostrar: existe $N$ tal que si $n > N$ entonces $\Big\| \Big(\overrightarrow{x_n}, \overrightarrow{y_n}\Big) \, – \, \Big(\overrightarrow{L}, \overrightarrow{M} \Big) \Big\| < \epsilon \big]$
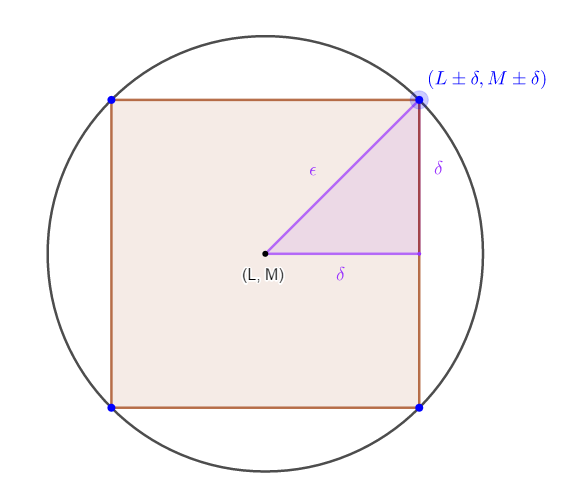
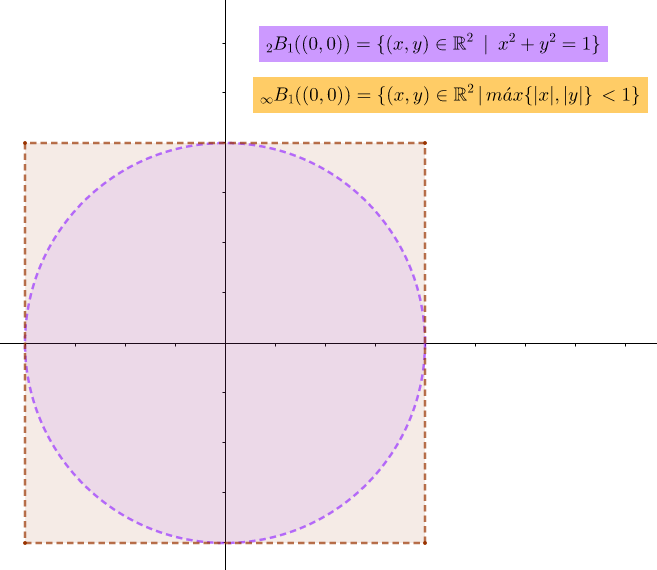
Dada la circunferencia $\big(x-L\big)^2+\big(y-M\big)^2=\epsilon^2$, queremos saber cuales son las coordenadas del cuadrado con lados paralelos a los ejes coordenados que está inscrito en la circunferencia.
Como $\Big\{\overrightarrow{x_n}\Big\} \longrightarrow \overrightarrow{L}$ para $\delta = \frac{\epsilon}{\sqrt{2}}$ existe $N_1$ tal que $n \geq N_1 \rightarrow \Big|\overrightarrow{x_n} \, – \, \overrightarrow{L} \Big| < \delta$…..$(1)$
Como $\Big\{\overrightarrow{y_n} \Big\} \Longrightarrow \overrightarrow{M}$ para $\delta = \frac{\epsilon}{\sqrt{2}}$ existe $N_2$ tal que $n \geq N_2 \rightarrow \Big|\overrightarrow{y_n} \, – \, \overrightarrow{M}\Big| < \delta$…..$(2)$
Por $(1)$ y $(2)$, para $n \geq máx \big\{N_1, N_2 \big\}$ tenemos que $$\Big|\overrightarrow{x_n} \, – \, \overrightarrow{L}\Big| < \delta \wedge \Big|\overrightarrow{y_n} \, – \, \overrightarrow{M}\Big| < \delta \Longrightarrow \Big(\overrightarrow{x_n}, \overrightarrow{y_n} \Big) \text{ está en el cuadrado con vértices} \Big(\overrightarrow{L}\pm \delta , \overrightarrow{M} \pm \delta \Big)$$
Entonces $\Big(\overrightarrow{x_n}, \overrightarrow{y_n} \Big)$ está en el círculo.$_{\blacksquare}$