(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
El determinante de una matriz es un valor numérico que se puede calcular a partir de los elementos de la matriz y que tiene muchas aplicaciones en álgebra lineal y otras áreas de las matemáticas y la física. Una forma de calcular el determinante es mediante la definición en términos de permutaciones.
En esta definición, se considera una matriz cuadrada y se toman todas las posibles permutaciones de las filas o columnas de la matriz. Para cada permutación, se calcula un producto de elementos de la matriz, donde cada elemento proviene de una fila o columna diferente, y se suman todos estos productos. El resultado de esta suma es el determinante de la matriz.
Esta definición puede parecer complicada al principio, pero es muy poderosa y se puede utilizar para calcular determinantes de matrices de cualquier tamaño. Además, tiene muchas propiedades útiles, como la linealidad en las filas o columnas de la matriz, que permiten simplificar muchos cálculos.
En el siguiente video de 3Blue1Brown se da una aproximación geométrica e intuitiva de lo que es el determinante.
Ve el siguiente video de la clase.
Antes de llegar a la definición de lo que es un determinante analicemos lo que es una permutación.
Definición
Las permutaciones de $n$ elementos son:
$S_n=\set{\sigma:\set{1,\dotsc,n}\to\set{1,\dotsc,n}\mid \sigma\,\,es\,\,biyectiva }$
Una permutación $\sigma \in S_n$ se llama una transposición si intercambia dos números y deja fijos a los demás.
Nota
Toda permutación es composición de transposiciones. Puede que haya varias composiciones que den la misma permutación, pero todos son la composición de un número par de transposiciones o todas son la composición de un número impar de transposiciones.
Definición
Sea $\sigma \in S_n$. Decimos que $\sigma$ es par si es la composición de un número par de transposiciones, e impar en caso contrario.
El signo de $\sigma$ es $+1$ en el primer caso y $-1$ en el segundo caso y se denota por $sgn\,\sigma.$
Ejemplo
Considera el conjunto
$S_3=\set{\sigma:\set{1,2,3}\to\set{1,2,3}\mid \sigma\,\,es\,\,biyectiva }.$
Podemos dar todos elementos del conjunto, es decir todas las funciones biyectivas :
$\sigma_1=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 1 & 2 & 3 \end{array}\right) \end{equation*}$, $\sigma_2=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 1 & 3 \end{array}\right) \end{equation*}$, $\sigma_3=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 1 & 3 & 2 \end{array}\right) \end{equation*}$, $\sigma_4=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 2 & 1 \end{array}\right) \end{equation*}$, $\sigma_5=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 3 & 1 \end{array}\right) \end{equation*}$, $\sigma_6=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 1 & 2 \end{array}\right) \end{equation*}.$
¿Cuál es el signo de $\sigma_2$?
$\sigma_2=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 1 & 3 \end{array}\right) \end{equation*}$ es un transposición ya que intercambia el $1$ con el $2$ y deja fijo al $3$, entonces $\sigma_2$ es impar y $sgn\,\sigma_2=-1$.
Observa que $\sigma_3=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 1 & 3 & 2 \end{array}\right) \end{equation*}$ y $\sigma_4=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 2 & 1 \end{array}\right) \end{equation*}$ también son transposiciones y por lo tanto también su signo es $-1$.
¿Cuál es el signo de $\sigma_1$?
Observa que la composición de $\sigma_2\circ \sigma_2=\sigma_1$.
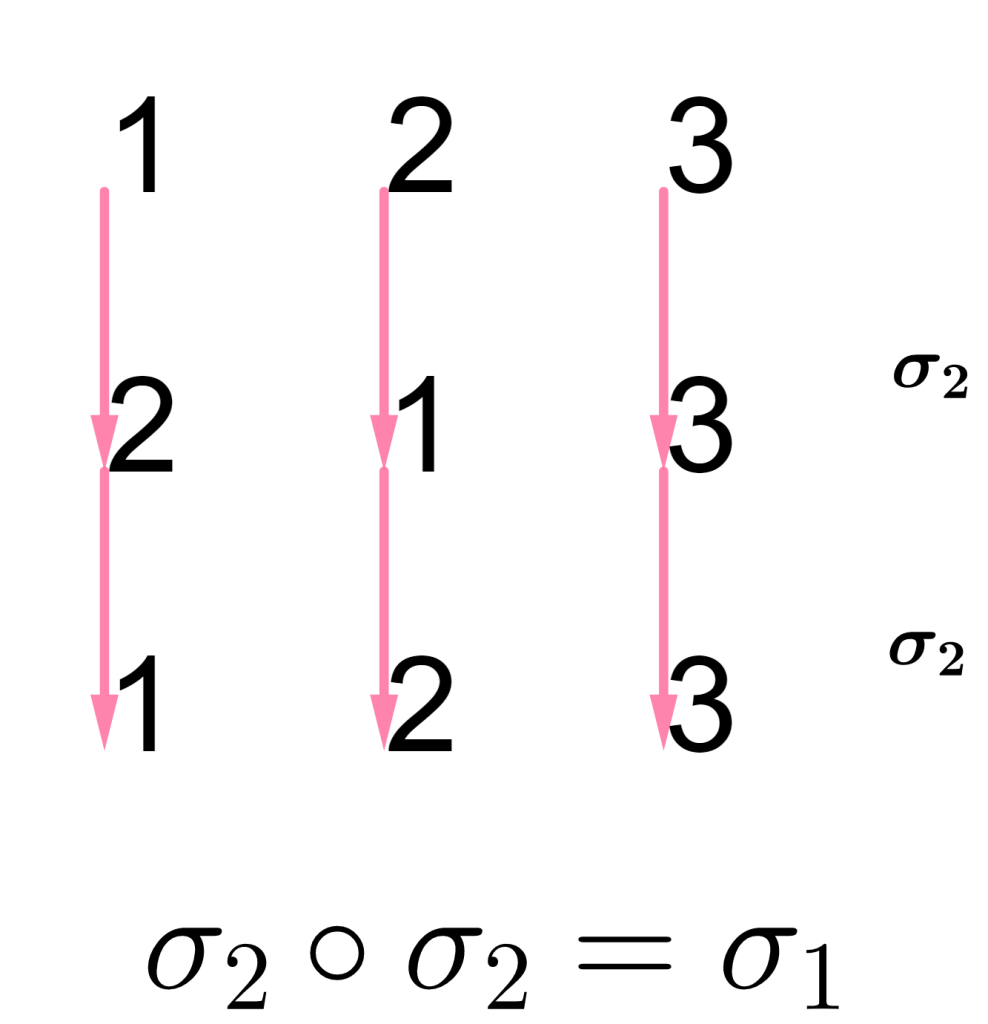
Como $\sigma_2\circ \sigma_2=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 1 & 2 & 3 \end{array}\right) \end{equation*}$ $=\sigma_1$, siendo $\sigma_2$ una transposición, entonces $\sigma_1$ es par pues la composición de $\sigma_2$ con si misma. Su signo por lo tanto es $1$, $sgn\,\sigma_1=+1$.
¿Cuál es el signo de $\sigma_5$?
Observa que la composición de $\sigma_2=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 1 & 3 \end{array}\right) \end{equation*}$ con $\sigma_4=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 2 & 1 \end{array}\right) \end{equation*}$ nos da $\sigma_5=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 3 & 1 \end{array}\right) \end{equation*}.$
Así, $\sigma_4\circ \sigma_2=\sigma_5$, con $\sigma_4$ y $\sigma_2$ transposiciones.
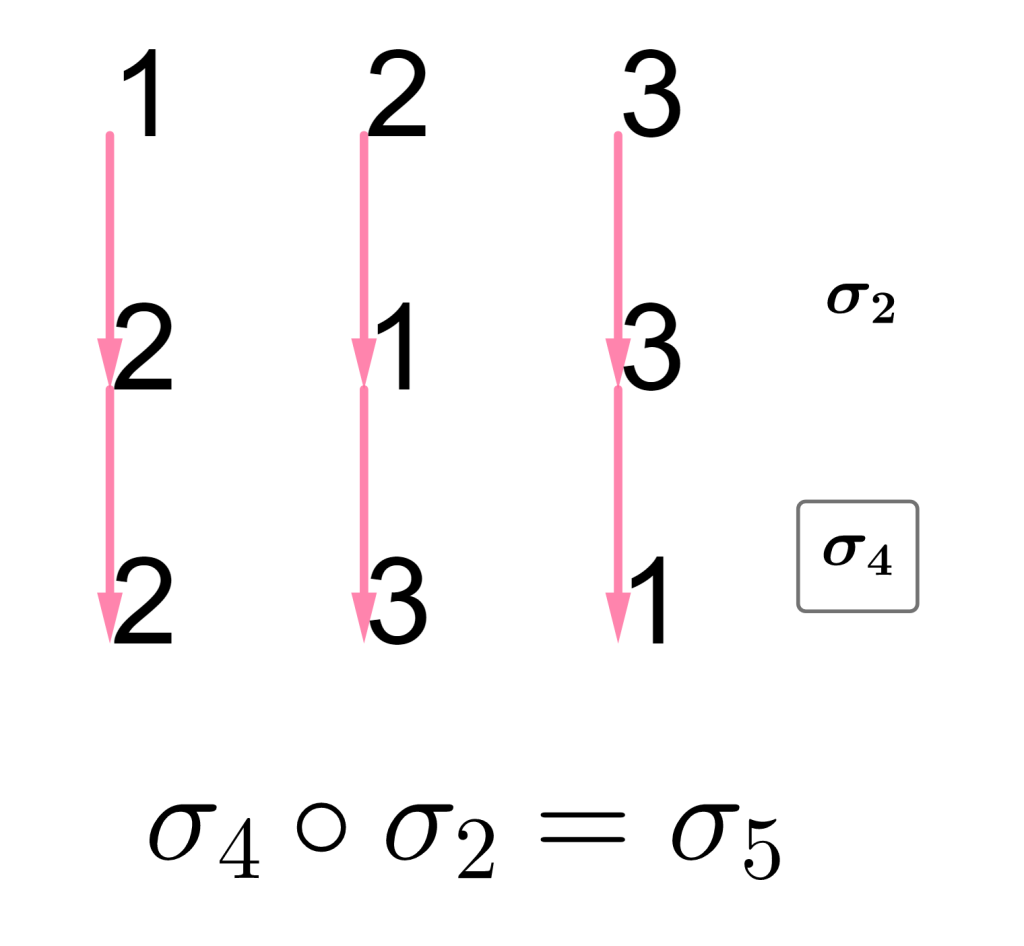
Concluimos que $\sigma_5$ es par y por tanto $sgn\,\sigma_5$=+1.$
¿Cuál es el signo de $\sigma_6$?
La composición de $\sigma_4=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 2 & 1 \end{array}\right) \end{equation*}$ con $\sigma_2=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 1 & 3 \end{array}\right) \end{equation*}$ nos da $\sigma_6=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 1 & 2 \end{array}\right) \end{equation*}.$
Así, $\sigma_2\circ \sigma_4=\sigma_6$, con $\sigma_2$ y $\sigma_4$ transposiciones.
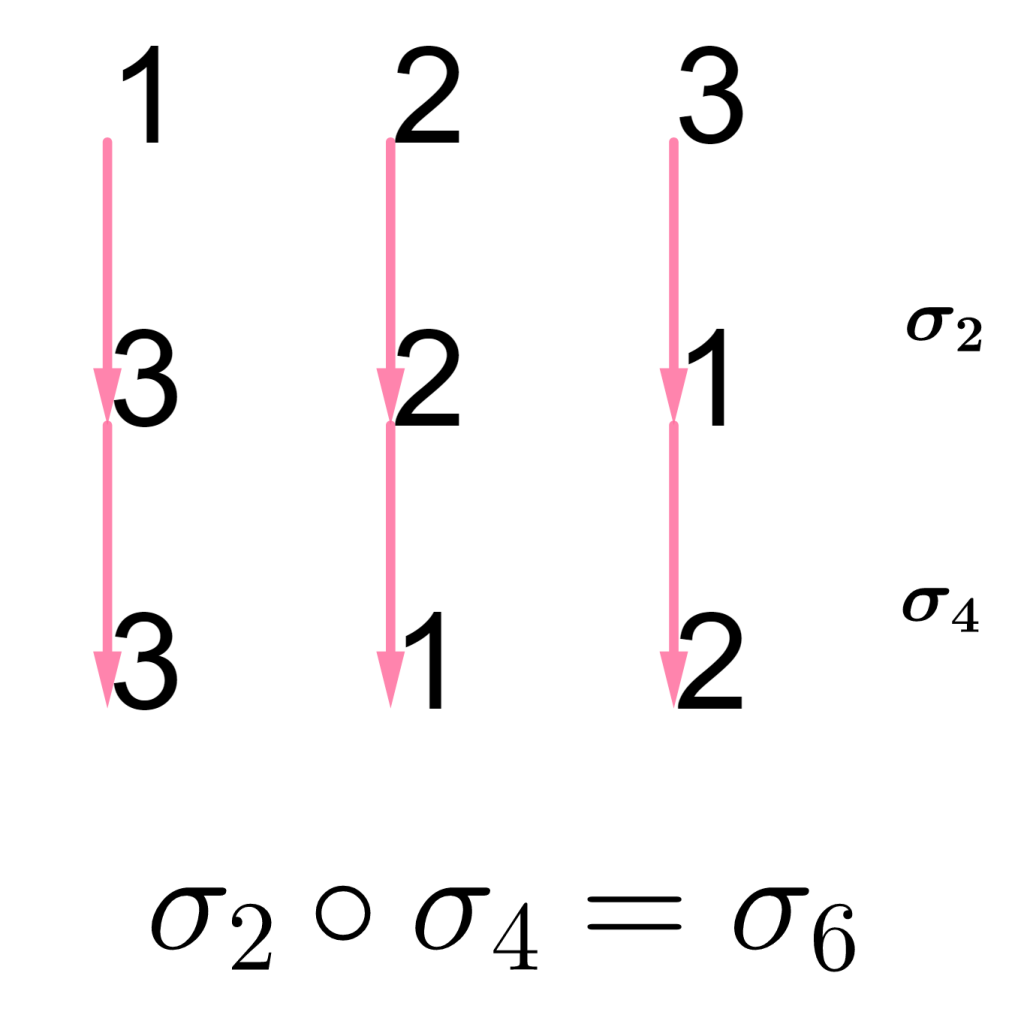
Concluimos que $\sigma_6$ es par y por tanto su signo es $+1$.
Observemos que $\sigma_6=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 3 & 1 & 2 \end{array}\right) \end{equation*}$ es la inversa de $\sigma_5=\begin{equation*} \left(\begin{array}{rrr} 1 & 2 & 3\\ 2 & 3 & 1 \end{array}\right) \end{equation*}$, por eso es la composición de las mismas transposiciones que $\sigma_5$ pero en orden inverso.
Los que acabamos de ver es que:
$\sigma_1,\sigma_5,\sigma_6$ son pares y $\sigma_2,\sigma_3,\sigma_4$ son impares.
Con estos elementos vamos a dar la definición de lo que es el determinante de una matriz.
Ve el siguiente video
Definición
Sea $A\in \mathscr M_{n\times n}(\mathbb R)$. El determinante de $A$ es:
$\det\,A=\displaystyle\sum_{\sigma\in S_n}sgn\,\sigma\,a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)}$
Observación Sea $A=\begin{equation*} \left(\begin{array}{rr} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}\right) \end{equation*}$, entonces
$\det\,A=a_{11}a_{22}-a_{12}a_{21}.$
Esto se debe a que las únicas permutaciones de $\{1,2\}$ son $\sigma_1=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 1 & 2 \end{array}\right) \end{equation*}$, que es la identidad y tiene signo $+1$, y la transposición $\sigma_2=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 2 & 1 \end{array}\right) \end{equation*}$ que tiene signo $-1.$ Así,
$\det\,A=sgn\,\sigma_1\,a_{1\sigma_1(1)}a_{2\sigma_1(2)}+sgn\,\sigma_2\,a_{1\sigma_2(1)}a_{2\sigma_2(2)}=(+1)\,a_{11}a_{22}+(-1)\,a_{12}a_{21}=a_{11}a_{22}-a_{12}a_{21}.$
Ejemplos.
En estos ejemplos veremos lo que sucede con el determinante, cuando aplicamos las distintas operaciones elementales a una matriz.
$1.$ Considera las matrices $A=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 3 & 4 \\ \end{array}\right) \end{equation*}$, $A’=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ -1 &5 \\ \end{array}\right) \end{equation*}$, $A^{\prime\prime}=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 2 & 9 \\ \end{array}\right) \end{equation*}.$
Si obtenemos sus determinantes tenemos que:
$det\,A’=4-6=-2,\,\,det\,A^{\prime\prime}=5-(-2)=7\,\,,det\,A=9-4=5$
Observa que en este ejemplo, el segundo renglón de $A^{\prime\prime}$ se obtiene de la suma de los segundos renglones de $A$ y $A^{\prime\prime}$, y su primer renglón coincide con los de $A$ y $A^{\prime}$,
Y lo que estamos observando es que:
$det\,A^{\prime\prime}=det\,A+det\,A^{\prime}$.
$2.$ Sean $A’=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 3 & 4 \\ \end{array}\right) \end{equation*}$ y $A=\begin{equation*} \left(\begin{array}{rr} 3 & 6 \\ 3 & 4 \\ \end{array}\right) \end{equation*}.$
El primer renglón de $A$ se obtiene multiplicando por $3$ el primer renglón de $A’$
Los determinantes de estas matrices son:
$det\,A’=4-6=-2,\,\,det\,A=12-18=-6$
y lo que estamos observando es que:
$det\,A=3det\,A’.$
$3.$ Veamos qué sucede con el determinante cuando intercambiamos renglones en una matriz. Considera las matrices:
$A’=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 3 & 4 \\ \end{array}\right) \end{equation*}$ y $A=\begin{equation*} \left(\begin{array}{rr} 3 & 4 \\ 1 & 2 \\ \end{array}\right) \end{equation*},$
$det\,A’=4-6=-2,\,\,det\,A=6-4=2.$
En este caso tenemos que:
$det\,A=-det\,A’.$
$4.$ Veamos qué pasa cuando en una matriz hay dos renglones iguales.
Sea $A=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 1 & 2 \\ \end{array}\right) \end{equation*},$ entonces
$det\,A=2-2=0$, es decir el determinante vale cero.
$5.$ Veamos qué pasa cuando le sumamos a un renglón un múltiplo de otro.
Sea $A’=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 3 & 4 \\ \end{array}\right) \end{equation*}$ y considera su matriz equivalente $A=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 1 & 0 \\ \end{array}\right) \end{equation*}$, que se obtiene de $A’$, sumando al renglón dos de $A’$ menos dos veces el primero.
Entonces $det\,A’=4-6=-2,\,\,det\,A=0-2=-2.$ En este caso
$det\,A=det\,A’.$
es decir el determinante coincide.
$6.$ Consideremos una matriz con un renglón de ceros, por ejemplo
$A=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 0 & 0 \\ \end{array}\right) \end{equation*}.$ Notamos que su determinante es $det\,A=0-0=0$.
$7.$ Por último veamos qué pasa con el determinante al transponer una matriz.
Sean $A=\begin{equation*} \left(\begin{array}{rr} 1 & 2 \\ 3 & 4 \\ \end{array}\right) \end{equation*}$ y considera su transpuesta $A^t=\begin{equation*} \left(\begin{array}{rr} 1 & 3 \\ 2 & 4 \\ \end{array}\right) \end{equation*}$
Si calculamos sus determinantes tenemos que:
$det\,A=4-6=-2,\,\,det\,A=4-6=-2.$
En este caso:
$det\,A=det\,A^t.$
Tarea Moral
$1.$ Encuentra todas las permutaciones de $\set{1,2,3,4}$ y su signo. ¿Cuántas hay en total?, ¿Cuántas son pares?
$2.$ Sea $A=\begin{equation*} \left(\begin{array}{rr} -3& 1 \\ 7 & 9 \\ \end{array}\right) \end{equation*}$ y calcula:
$i)$ Su determinante.
$ii)$ El $det\,B$, donde $B$ se obtiene de $A$ multiplicando su segundo renglón por $4.$
$iii)$ El $det\,C$, donde $C$ se obtiene de $A$ intercambiando sus renglones entre sí.
$iv)$ El $det\,D$, donde $D$ se obtiene de $A$ sumando al segundo renglón dos veces el primero.
Más adelante
En la siguiente nota veremos que las propiedades observadas en los ejemplos se cumplen en general, para ello usaremos la definición que dimos de determinante.
Enlaces relacionados
Enlace a la nota anterior. Nota 39. Ejemplos de sistemas de ecuaciones.
Enlace a la nota siguiente. Nota 41. Propiedades de los determinantes.
