(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta nota veremos como cuantificar el número de ordenaciones de $n$ objetos cuando son tomadas de $m$ en $m$ de ellos, para ello obtendremos el cardinal del número de funciones inyectivas del conjunto de los primeros $m$ naturales, en el conjunto de $n$ objetos.
Definición
Sean $n,m\in \mathbb N$. Dado un conjunto $A=\set{a_1,\dotsc ,a_n}$ con $n$ elementos, las ordenaciones de los elementos de $A$ tomados de $m$ en $m$ son las funciones inyectivas de $\set{1,\dotsc, m}$ en $A$. Al número de ordenaciones de los elementos de un conjunto con $n$ elementos, tomados de $m$ en $m$, lo denotaremos por $O_{n}^{m}$.
$O_{n}^{m}=\#\set{f\mid f:\set{1,\dotsc, m}\to A=\set{a_1,\dotsc ,a_n}, con\\\ f \\\ inyectiva}$
Observa que si $m>n$ entonces $O_{n}^{m}$ es cero.
Ejemplo
¿Cuántas banderas tricolores se pueden formar con rojo, naranja, verde, azul y morado?
Consideremos la bandera tricolor rojo, azul, naranja.

En el lugar $1$ asignamos el rojo, en el $2$ el azul y en el $3$ el naranja. Podemos verla como una función de $\set{1,2,3}$ en $A$, con $A$ el conjunto formado por los colores rojo, naranja, verde, azul y morado, es decir $A=\{rojo, naranja, verde, azul,morado\}$. En este caso la función sería:
$f: \set{1,2,3} \to A$ con $f(1)=rojo$, $f(2)=azul$, $f(3)=naranja.$
Veamos primero cuántas banderas tricolor hay que terminen en naranja.
Para ello debemos considerar todas las posibles maneras de iniciar una bandera que termine en naranja, lo cual corresponde a todas las formas de crear una bandera bicolor con los colores restantes. Las banderas bicolores formadas con rojo, verde, azul o morado son:
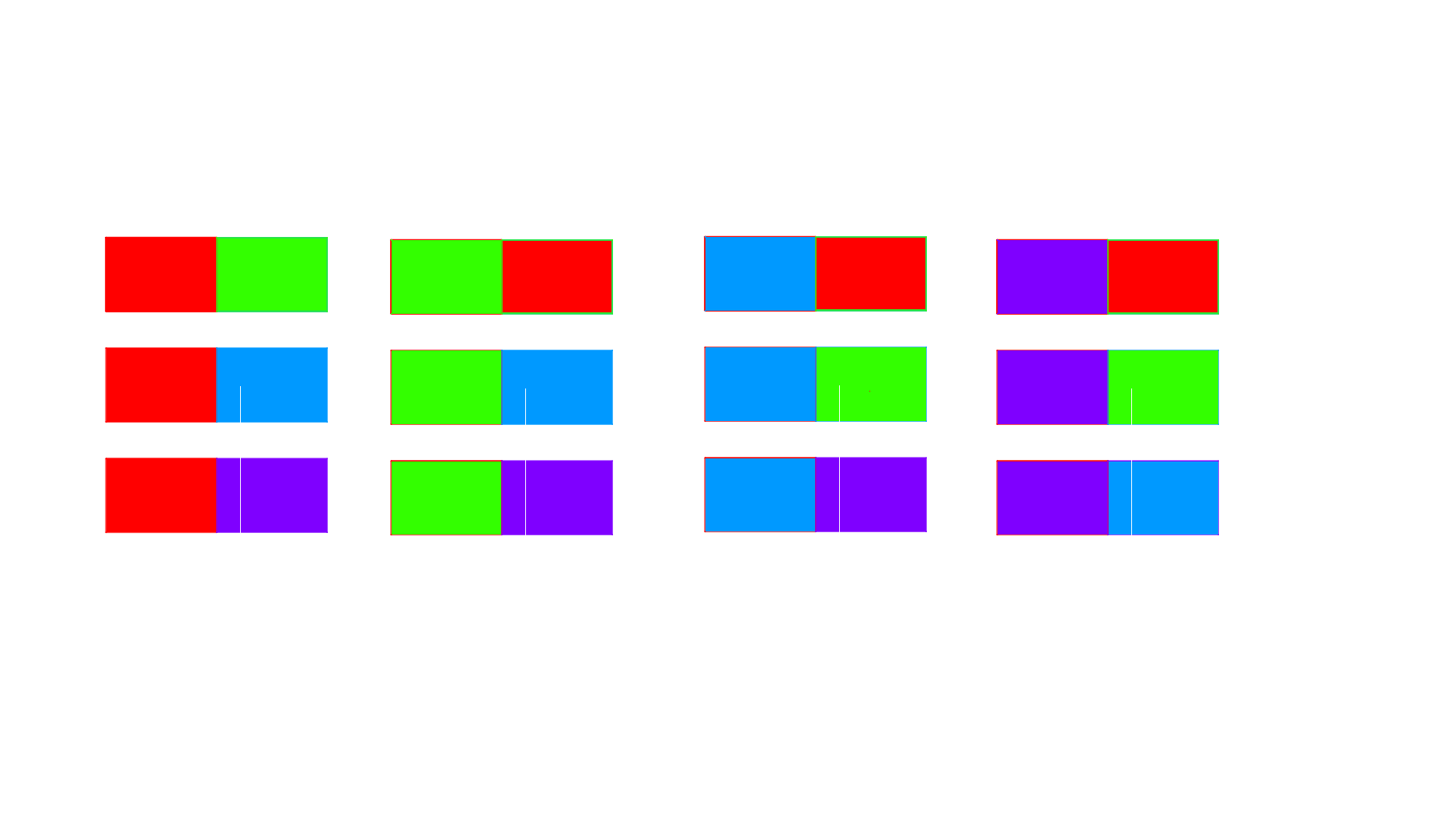
Hay 12 banderas bicolor con estos $4$ colores.
Fíjate que entonces hay $12$ banderas tricolor que terminan en naranja. De manera similar hay 12 que terminan rojo, 12 en verde, 12 en azul y 12 en morado, doce por cada color. Éstas son el total de las ordenaciones de 4 elementos tomadas de 2 en 2, $O_{4}^{2}$, el número de banderas tricolor es entonces:
$5\cdot 12=5\cdot O_{4}^{2}= O_{5}^{3}=60.$
Observa que $ O_{5}^{3} =5\cdot O_{4}^{2}$, probaremos que esto es válido en general y que $ O_{n+1}^{m+1} =(n+1)\cdot O_{n}^{m}$.
Lema
Sean $n,m\in \mathbb N^+$, $n\geq m$, entonces $O_{n+1}^{m+1}=(n+1)\cdot O_{n}^{m} $.
Demostración
Sean $n,m\in \mathbb N^+$, $n\geq m$ y $A=\set{a_1\dotsc,a_n,a_{n+1}}$ con $n+1$ elementos.
$O_{n+1}^{m+1}=\#\set{f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}}\mid f \\\ es\\\ inyectiva}$.
Para cada $i\in \set{1,\dotsc,n+1}$ consideremos el siguiente conjunto:
$B_{i}=\set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva\\\ y \\\ f(m+1)=a_i }$.
Estamos considerando sólo aquellas funciones que mandan al último elemento del dominio, $m+1$, a $a_i\in A$.
Cada una de estas funciones está determinada por su restricción a $\set{1,\dotsc, m}$, que es una función inyectiva de $\set{1,\dotsc, m}$ en $A$, y como en la imagen no aparecerá el elemento $a_i$, se puede considerar como una función inyectiva de $\set{1,\dotsc, m}$ en $A\setminus \set{a_i}$ (conjunto que tiene $n$ elementos). Entonces por la notación establecida para el número de ordenaciones:
$\#B_i=O_{n}^{m}$
Pero $ \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva}$ es la unión disjunta de $B_1,\dotsc, B_{n+1}$, es decir:
$B_1\cup \dotsc \cup B_{n+1}= \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva}$.
Por lo que
$\#(B_1\cup \dotsc \cup B_{n+1})= \# \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}}\mid f \\\ es \\\ inyectiva}.$
Y por el principio generalizado de la suma tenemos que:
$\#B_1+ \dotsc + \# B_{n+1}= \# \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}}\mid f \\\ es \\\ inyectiva}.$
Como $\#B_i=O_{n}^{m}$, para todo $i\in\set{1,\dotsc,n+1}$, entonces
$(n+1)\cdot O_{n}^{m}= \# \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva}.$
Y por lo tanto:
$ O_{n+1}^{m+1} =(n+1)\cdot O_{n}^{m} .$
$\square$
Ejemplo
En la fila de un avión hay $3$ lugares, ¿de cuántas formas podemos llenarla eligiendo a personas de una familia de 6 integrantes? o bien, ¿Cuántas ordenaciones hay de un conjunto con $6$ elementos tomados de $3$ en $3$?
Sabemos que:
$O_{6}^{3}=6\cdot O_{2}^{5}= 6\cdot5 \cdot O_{4}^{1}.$
Pero si $A=\set{a_1,a_2,a_3,a_4}$ es un conjunto con cuatro elementos, habrá $4$ funciones inyectivas de $\set{1}$ en $A$ y por lo tanto $ O_{4}^{1} =4$. Así:
$O_{6}^{3}=6\cdot5 \cdot 4=120$, y por lo tanto hay $120$ maneras de llenar la fila.
Teorema
Sean $n,m\in \mathbb N^+$, $n\geq m$, entonces $O_{n}^{m}=n(n-1)\dotsc(n-m+1)$
Demostración
Sean $n,m\in \mathbb N^+$, $n\geq m$
Haremos la prueba por inducción sobre $m$
Si $m=1$ consideremos $A=\set{a_1,\dotsc,a_n}$ con $n$ elementos. Tenemos que hay $n$ funciones inyectivas de $\set{1}$ en $A$, así:
$O_{n}^{1}=n=n-1+1$ y en este caso se cumple la fórmula.
Supongamos que resultado se cumple para $m$, es decir que $O_{t}^{m}=t(t-1)\dotsc (t-m+1)$ para toda $t\geq m$, que es nuestra hipótesis de inducción.
Sea $n\geq m+1$.
Si consideramos $O_{n}^{m+1}= O_{(n-1)+1}^{m+1} $, por el lema anterior esto es igual a
$ O_{(n-1)+1}^{m+1}=[(n-1)+1] O_{n-1}^{m} .$
Como $n-1\geq m$ usando la hipótesis de inducción tenemos que
$ O_{n-1}^{m} = (n-1)(n-2)\dotsc ((n-1)-m+1)$
de donde
$ O_{(n-1)+1}^{m+1}=[(n-1)+1] O_{n-1}^{m} = [(n-1)+1] (n-1)(n-2)\dotsc ((n-1)-m+1)$
Así $ O_{n}^{m+1}=[(n-1)+1] O_{n-1}^{m} = n(n-1)(n-2)\dotsc (n-m)$, probando con ello que el resultado se cumple para $m+1$.
Por el principio de inducción la fórmula se cumple para toda $m$.
$\square$
Tarea Moral
1. Entre un grupo de 7 personas se debe elegir una mesa directiva con un presidente, un secretario, un vocal y un suplente ¿de cuántas maneras se puede elegir esa mesa directiva?
2. En un concurso participan 30 alumnos y se decidirá quién se lleva cada uno de los tres primeros lugares ¿cuántos posibles resultados se tienen como ganadores del concurso?
3. i) ¿De cuántas maneras pueden posar tres hombres y dos mujeres en línea para una fotografía de grupo?
ii) ¿De cuántas maneras pueden colocarse en línea si una mujer debe estar en cada extremo?
iii) ¿De cuántas maneras las personas del mismo sexo están juntas?
Más adelante
En la siguiente nota continuaremos el estudio de las técnicas de conteo, daremos la definición formal de combinaciones, que son el número de subconjuntos de un conjunto dado.
Enlaces relacionados
Enlace a la nota anterior. Nota 21. Conteo, ordenaciones con repetición.
Enlace a la nota siguiente. Nota 23. Combinaciones.
