Introducción

Ya hemos definido qué es el gradiente $\mathrm{\nabla }f$ de un campo escalar $f$. Hemos visto cómo está relacionado con las derivadas direccionales. Así mismo, mostramos que conocer este gradiente nos permite dar información sobre los máximos y mínimos del campo escalar. En esta entrada mostraremos una propiedad más del gradiente: que nos ayuda a dar una generalización del teorema del valor medio de Cálculo I, pero para campos escalares. Este será un resultado fundamental para demostrar otras propiedades de los campos escalares. Como ejemplo, también damos en esta entrada un criterio suficiente para que un campo escalar sea diferenciable.

Teorema del valor medio para funciones de $\mathbb{R}$ en $\mathbb{R}$

Para facilitar la lectura de este material, recordemos lo que nos dice el teorema del valor medio sencillo, es decir, el de $\mathbb{R}$ en $\mathbb{R}$.

Teorema. Sean $a<b$ reales. Sea $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe algún punto $c\in (a,b)$ tal que $$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}.$$

Una vez que uno interpreta el teorema gráficamente, se vuelve muy intuitivo. Considera la siguiente figura.

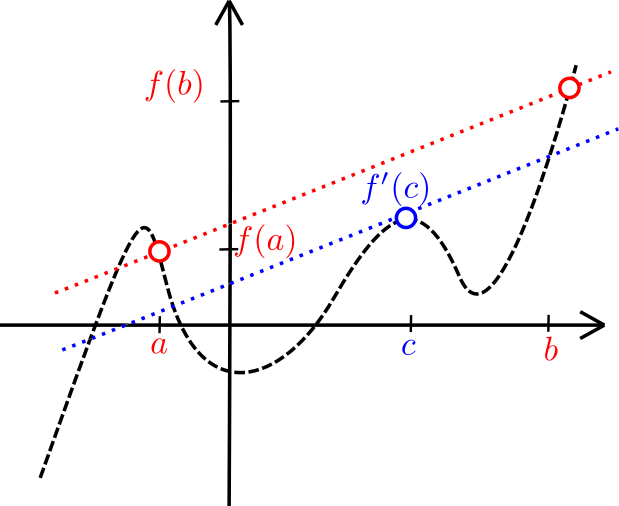
El término $$\frac{f(b)-f(a)}{b-a}$$ es la pendiente del segmento que une los puntos $(a,f(a))$ y $(b,f(b))$ El término $f^{\prime }(c)$ va marcando la pendiente de la recta tangente a $f$ en cada punto $c$. En términos geométricos, lo que nos dice este teorema es que para algún valor de $c$, la pendiente de la recta tangente en $c$ es la pendiente del segmento entre los extremos.

Lo que haremos a continuación es dar una generalización apropiada para funciones de ${\mathbb{R}}^n$ a $\mathbb{R}$.

Teorema del valor medio para funciones de ${\mathbb{R}}^n$ en $\mathbb{R}$

Para generalizar el teorema del valor medio a funciones de ${\mathbb{R}}^n$ a $\mathbb{R}$, necesitaremos cambiar un poco las hipótesis. El segmento $[a,b]$ que usábamos ahora será un segmento (multidimensional) que conecte a dos vectores $\overline{x}$ y $\overline{y}$ en ${\mathbb{R}}^n$. La diferenciabilidad la pediremos en todo un abierto que contenga al segmento. El enunciado apropiado se encuentra a continuación.

Teorema (del valor medio para campos escalares). Sea $S$ un abierto de ${\mathbb{R}}^n$. Tomemos $f:S\subseteq {\mathbb{R}}^n\to \mathbb{R}$ un campo escalar diferenciable. Sean $\overline{x}$ y $\overline{y}$ en $S$ tales que el segmento que une a $\overline{x}$ con $\overline{y}$ se queda contenido en $S$. Entonces, existe $c\in (0,1)$ tal que $$\mathrm{\nabla }f((1-c)\overline{x}+c\overline{y})\cdot (\overline{y}-\overline{x})=f(\overline{y})-f(\overline{x}).$$

En este caso no podemos «pasar dividiendo $\overline{y}-\overline{x}$» pues no tiene sentido dividir entre vectores. Pero en el caso $n=1$ sí se puede, y justo obtenemos de vuelta el teorema del valor medio de $\mathbb{R}$ en $\mathbb{R}$. Uno podría pensar que entonces esta es una manera alternativa de demostrar el teorema para funciones de $\mathbb{R}$ en $\mathbb{R}$. Sin embargo, como veremos a continuación, la demostración de la versión para campos escalares usa la versión para funciones reales.

Demostración. Consideremos la función $\gamma :[0,1]\to {\mathbb{R}}^n$ dada $\gamma (t)=(1-t)\overline{x}+t\overline{y}$. Notemos que $\gamma$ es diferenciable, con ${\gamma }^{\prime }(t)=\overline{y}-\overline{x}$. Además, por hipótesis $f$ es diferenciable en $S$. Así, $f\circ \gamma :[0,1]\to \mathbb{R}$ también es diferenciable, y por regla de la cadena

$$\begin{array}{rl}(f\circ \gamma {)}^{\prime }(t)& =\mathrm{\nabla }f(\gamma (t))\cdot {\gamma }^{\prime }(t)\\ & =\mathrm{\nabla }f(\gamma (t))\cdot (\overline{y}-\overline{x}).\end{array}$$

¡Pero $f\circ \gamma$ ya es una función de $\mathbb{R}$ en $\mathbb{R}$! Así, podemos aplicarle el teorema del valor medio real (verifica las hipótesis como tarea moral). Al hacer esto, obtenemos que existe una $c\in (0,1)$ tal que
$$\begin{array}{rl}(f\circ \gamma {)}^{\prime }(c)& =\frac{(f\circ \gamma )(1)-(f\circ \gamma )(0)}{1-0}\\ & =f(\overline{y})-f(\overline{x}).\end{array}$$

Usando la fórmula que obtuvimos por regla de la cadena para $(f\circ \gamma {)}^{\prime }$ y la definición de $\gamma$ obtenemos que

$$\mathrm{\nabla }f((1-c)\overline{x}+c\overline{y})\cdot (\overline{y}-\overline{x})=f(\overline{y})-f(\overline{x}),$$

tal y como buscábamos.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

En el teorema anterior estamos pidiendo que $f$ sea diferenciable. Sin embargo, basta con que exista la derivada de la composición en el segmento que nos interesa y el resultado también se sigue. Es decir, tenemos la siguiente versión con una hipótesis más débil. La enunciamos pues la usaremos en la siguiente sección.

Teorema (del valor medio para campos escalares, hipótesis debilitada). Sea $S$ un abierto de ${\mathbb{R}}^n$. Tomemos $f:S\subseteq {\mathbb{R}}^n\to \mathbb{R}$ un campo escalar. Sean $\overline{x}$ y $\overline{y}$ en $S$ tales que el segmento que une a $\overline{x}$ con $\overline{y}$ se queda contenido en $S$ y tales que para toda $c\in [0,1]$ se cumple que la derivada (real) de $f((1-c)\overline{x}+c\overline{y}))$ existe. Entonces, existe $c\in (0,1)$ tal que $$\mathrm{\nabla }f((1-c)\overline{x}+c\overline{y})\cdot (\overline{y}-\overline{x})=f(\overline{y})-f(\overline{x}).$$

La demostración es exactamente la misma.

Aplicación del teorema del valor medio

Como primera aplicación del teorema del valor medio para campos escalares mostraremos un criterio de diferenciabilidad muy útil, al que llamaremos el teorema de diferenciabilidad y derivadas parciales.

Teorema. Sea $f:S\subseteq {\mathbb{R}}^n\to \mathbb{R}$ un campo escalar. Supongamos que para cierto punto $\overline{a}\in S$ y cierta vecindad $B_r(\overline{a})\subset S$ existen las derivadas parciales $\frac{\partial f}{\partial x_1},\dots ,\frac{\partial f}{\partial x_n}$ y son continuas en $\overline{a}$. Entonces $f$ es diferenciable en $\overline{a}$.

Demostración. Elijamos un vector $\overline{u}=u_1{\hat{e}}_1+\cdots +u_n{\hat{e}}_n$ de norma $1$ y tomemos $\overline{v}=\lambda \overline{u}$ con $\lambda$ suficientemente chico como para que $\overline{a}+\overline{v}$ esté en $B_r(\overline{a})$. Definamos los siguientes vectores:

$$\begin{array}{rl}{\overline{v}}_0& =\overline{0}\\ {\overline{v}}_1& =u_1{\hat{e}}_1\\ {\overline{v}}_2& =u_1{\hat{e}}_1+u_2{\hat{e}}_2\\ & ⋮\\ {\overline{v}}_n& =u_1{\hat{e}}_1+u_2{\hat{e}}_2+\dots +u_n{\hat{e}}_n=\overline{u}.\end{array}$$

Con ellos creamos la siguiente suma telescópica para expresar a $f(\overline{a}+\overline{v})-f(\overline{a})$

$$\begin{array}{rl}f(\overline{a}+\overline{v})-f(\overline{a})& =f(\overline{a}+\lambda \overline{u})-f(\overline{a})\\ \text{(1)}& & =\sum _{k=1}^n[f(\overline{a}+\lambda {\overline{v}}_k)-f(\overline{a}+\lambda {\overline{v}}_{k-1})]\end{array}$$

Notemos que el $k$-ésimo término de esta suma puede ser escrito como $$f(\overline{a}+\lambda {\overline{v}}_{k-1}+\lambda u_k{\hat{e}}_k)-f(\overline{a}+\lambda {\overline{v}}_{k-1}).$$ Para simplificar, definimos ${\overline{b}}_k=\overline{a}+\lambda {\overline{v}}_{k-1}$ y reescribiendo el $k$-ésimo término tenemos $$f({\overline{b}}_k+\lambda u_k{\hat{e}}_k)-f({\overline{b}}_k).$$

Aplicando el teorema del valor medio con hipótesis debilidada para campos escalares a los puntos ${\overline{b}}_k$ y ${\overline{b}}_k+\lambda u_k{\hat{e}}_k$ (verifica las hipótesis), tenemos que para cada $k$ existe ${\xi }_k\in (0,1)$ tal que

$$\begin{array}{rl}f({\overline{b}}_k+\lambda u_k{\hat{e}}_k)-f({\overline{b}}_k)& =▽f((1-{\xi }_k){\overline{b}}_k+{\xi }_k({\overline{b}}_k+\lambda u_k{\hat{e}}_k))\cdot (\lambda u_k{\hat{e}}_k)\\ & =\lambda u_k\frac{\partial f}{\partial x_k}({\overline{c}}_k),\end{array}$$

en donde hemos definido ${\overline{c}}_k:=(1-{\xi }_k){\overline{b}}_k+{\xi }_k({\overline{b}}_k+\lambda u_k{\hat{e}}_k)$, que es un punto en el segmento que une a ${\overline{b}}_k$ con ${\overline{b}}_k+\lambda u_k{\hat{e}}_k$.

Tenemos pues que podemos escribir al $k$-ésimo término como:

$$f({\hat{b}}_k+\lambda u_k{\hat{e}}_k)-f({\overline{b}}_k)=\lambda u_k\frac{\partial f}{\partial x_k}({\overline{c}}_k).$$

Notemos además que si $\lambda \to 0$, entonces ${\overline{b}}_k\to \overline{a}$, ${\overline{c}}_k\to a$ y $\overline{v}\to \overline{0}$.

Escribimos entonces la ecuación $\text{(1)}$ como:

$$\begin{array}{}\text{(2)}& f(\overline{a}+\overline{v})-f(\overline{a})=\lambda \sum _{k=1}^n{u}_k\frac{\partial f}{\partial x_k}({\overline{c}}_k)\end{array}$$

En unos momentos usaremos esta expresión. Antes de ello, estudiemos otro de los términos involucrados en la diferenciabilidad. Tenemos que:

$$\begin{array}{rl}▽f(\overline{a})\cdot \overline{v}& =▽f(\overline{a})\cdot \lambda u\\ & =\lambda ▽f(\overline{a})\cdot u\\ \text{(3)}& & =\lambda \sum _{k=1}^n{u}_k\frac{\partial f}{\partial x_k}(\overline{a}).\end{array}$$

Empecemos entonces a combinar lo visto hasta ahora para entender los términos en la definición de diferenciabilidad. Tenemos juntando $\text{(2)}$ y $\text{(3)}$ que

$$\begin{array}{rl}f(\overline{a}+\overline{v})-f(\overline{a})-▽f(\overline{a})\cdot v& =\lambda \sum _{k=1}^n{u}_k\frac{\partial f}{\partial x_k}({\overline{c}}_k)-\lambda \sum _{k=1}^n{u}_k\frac{\partial f}{\partial x_k}(\overline{a})\\ & =\lambda \sum _{k=1}^n{u}_k[\frac{\partial f}{\partial x_k}({\overline{c}}_k)-\frac{\partial f}{\partial x_k}(\overline{a})].\end{array}$$

Como mencionamos, si $\lambda \to 0$ entonces $\overline{v}\to \overline{0}$. Además, $||\overline{v}||=|\lambda |$. Así:

$$\underset{\overline{v}\to \overline{0}}{lim}\frac{|f(\overline{a}+\overline{v})-f(\overline{a})-▽f(\overline{a})\cdot \overline{v}|}{||\overline{v}||}=\underset{\lambda \to 0}{lim}\left|\sum _{k=1}^n[\frac{\partial f}{\partial x_k}({\overline{c}}_k)-\frac{\partial f}{\partial x_k}(\overline{a})]u_k\right|.$$

Veamos qué más sucede cuando $\lambda \to 0$. Ya notamos que ${\overline{c}}_k\to \overline{a}$, así que usando la continuidad de las derivadas parciales tenemos:

$$\underset{\lambda \to 0}{lim}\frac{\partial f}{\partial x_k}({\overline{c}}_k)=\underset{{\overline{c}}_k\to \overline{a}}{lim}\frac{\partial f}{\partial x_k}({\overline{c}}_k)=\frac{\partial f}{\partial x_k}(\overline{a}).$$

Aplicando desigualdad del trángulo en la suma, el límite buscado es menor o igual a

$$\underset{\lambda \to 0}{lim}\sum _{k=1}^n\left|[\frac{\partial f}{\partial x_k}({\overline{c}}_k)-\frac{\partial f}{\partial x_k}(\overline{a})]u_k\right|=0.$$

Y aquí cada sumando se va a $0$. La conclusión final es que

$$\underset{\overline{v}\to \overline{0}}{lim}\frac{|f(\overline{a}+\overline{v})-f(\overline{a})-▽f(\overline{a})\cdot \overline{v}|}{||\overline{v}||}=0,$$

de modo que $f$ es diferenciable en $\overline{a}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

El regreso del teorema anterior no se vale

El teorema de diferenciabilidad nos dice que si las derivadas parciales existen y son continuas, entonces la función es diferenciable. Sin embargo, el regreso de este teorema no se vale, en el sentido de que existen funciones diferenciables cuyas derivadas parciales no son continuas. En otras palabras, si las derivadas parciales no son continuas, no podemos descartar la diferenciablidad de una función.

A continuación esbozamos un ejemplo que deberás completar como tarea moral.

Ejemplo. Consideremos la función

$$f(x,y)=\{\begin{array}{ll}(x^2+y^2)\sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)& \text{si }(x,y)\ne (0,0)\\ 0& \text{si }(x,y)=(0,0)\end{array}$$

Se puede demostrar que $f$ es diferenciable en $(0,0)$. De manera intuitiva, la función queda entre las funciones $(x,y)\to x^2+y^2$ y $(x,y)\to -x^2-y^2$. Se puede usar un argumento de acotamiento para mostrar que el plano tangente coincide entonces con el de estas funciones en $(0,0)$ que es el plano $z=0$. Verifica los detalles de tarea moral.

Así mismo, se puede ver que las derivadas parciales en $(0,0)$ existen y que de hecho se satisface $$\frac{\partial f}{\partial x}(0,0)=\frac{\partial f}{\partial y}(0,0)=0.$$

Finalmente, se puede ver que las derivadas parciales no convergen a $0$. Fuera del $(0,0)$, tenemos por reglas de derivación que

$$\begin{array}{rl}\frac{\partial f}{\partial x}(x,y)& =2x\sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{x\cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}\\ \frac{\partial f}{\partial y}(x,y)& =2y\sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{y\cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}.\end{array}$$

Una manear de ver que estas no son contínuas es aproximándonos por un eje. Por ejemplo, puedes verificar que sobre el eje $x$, conforme $x\to 0$, tenemos que la primera parcial oscila entre $-1$ y $1$.

$\mathrm{△}$

Más adelante…

Hemos enunciado y demostrado una versión del teorema del valor medio para campos escalaras. Gracias a ella hemos podido mostrar que si un campo escalar tiene derivadas parciales continuas, entonces es diferenciable. Las aplicaciones del teorema del valor medio para campos escalares van más allá. En la siguiente entrada hablaremos de las derivadas parciales de orden superior. El teorema del valor medio para campos escalares nos permitirá demostrar que bajo ciertas condiciones, en cierto sentido estas derivadas parciales «conmutan».

Tarea moral

1. ¿Qué dice el teorema del valor medio para campos escalares para la función $f(x,y)=\sin (x)\cos (y)$ tomando como extremos los puntos $(0,\frac{\pi }{2})$ y $(\frac{\pi }{2},0)$? Verifica si puedes aplicar las hipótesis.
2. En la demostración del teorema del valor medio que dimos, verifica que la función $f\circ \gamma$ dada en efecto satisface las hipótesis del teorema del valor medio real.
3. Supongamos que $f:{\mathbb{R}}^n\to \mathbb{R}$ es diferenciable en un abierto $S$ que contiene al segmento cuyos extremos son ciertos vectores $\overline{x}$ y $\overline{y}$ de ${\mathbb{R}}^n$. Supongamos que $f(\overline{x})=f(\overline{y})$. ¿Será cierto siempre que $\mathrm{\nabla }f$ se anula en algún vector del segmento que une $x$ con $y$? Ten cuidado, pues hay un producto escalar involucrado. En caso de que no siempre sea cierto, ¿Qué es lo que sí puedes garantizar?
4. En la demostración del teorema de diferenciabilidad, verifica que se pueden usar las hipótesis del teorema del valor medio para campos escalares con hipótesis debilitada. Necesitarás ver que la derivada real que tiene que existir es justo una parcial de las que suponemos que existen, completa los detalles. Luego, verifica que en efecto la conclusión que obtuvimos es justo la que se obtiene. Observa además que no podemos usar el teorema del valor medio para campos diferenciables con la hipótesis usual pues necesitaríamos saber que $f$ es diferenciable, lo cual es justo lo que queremos mostrar.
5. Completa el contraejemplo al regreso del teorema de diferenciabilidad. Entre otras cosas, tienes que hacer lo siguiente:
   • Verificar que en efecto la función es diferenciable en $(0,0)$. Puedes proceder por definición o acotando como se sugiere.
   • Revisar que las parciales en $(0,0)$ en efecto existen y coinciden con lo que sabemos a partir de que el plano tangente en el origen es $(0,0)$.
   • Obtener paso a paso la fórmula que dimos para las parciales, usando lo que sabes de regla de la cadena, derivadas en $\mathbb{R}$, etc.
   • Verificar que ninguna de las dos derivadas parciales es continua, completando el argumento de que al acercarnos por los ejes tenemos oscilaciones.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral III
• Entrada anterior del curso: Puntos críticos
• Entrada siguiente del curso: Derivadas parciales de segundo orden