Introducción

En la sección anterior vimos dos criterios de convergencia para las series, el criterio de la raíz y el criterio de la razón. En esta sección veremos el criterio de la integral enunciado el siguiente teorema.

Criterio de la integral

Teo: (Criterio de la integral)

Sea $f$ una función continua, positiva y decreciente en $[1,\mathrm{\infty })$ y sea $\left\{a_n\right\}$ una sucesión tal que $a_n=f(n)$ entonces:

$$\sum _{n=\mathrm{\infty }}^{\mathrm{\infty }}{a}_{n}converge\iff {\int }_1^{\mathrm{\infty }}f(x)dxconverge$$

Demostración:

$\Rightarrow ⌟$

Supongamos que $\sum _{i=1}^n{a}_n$ converge.

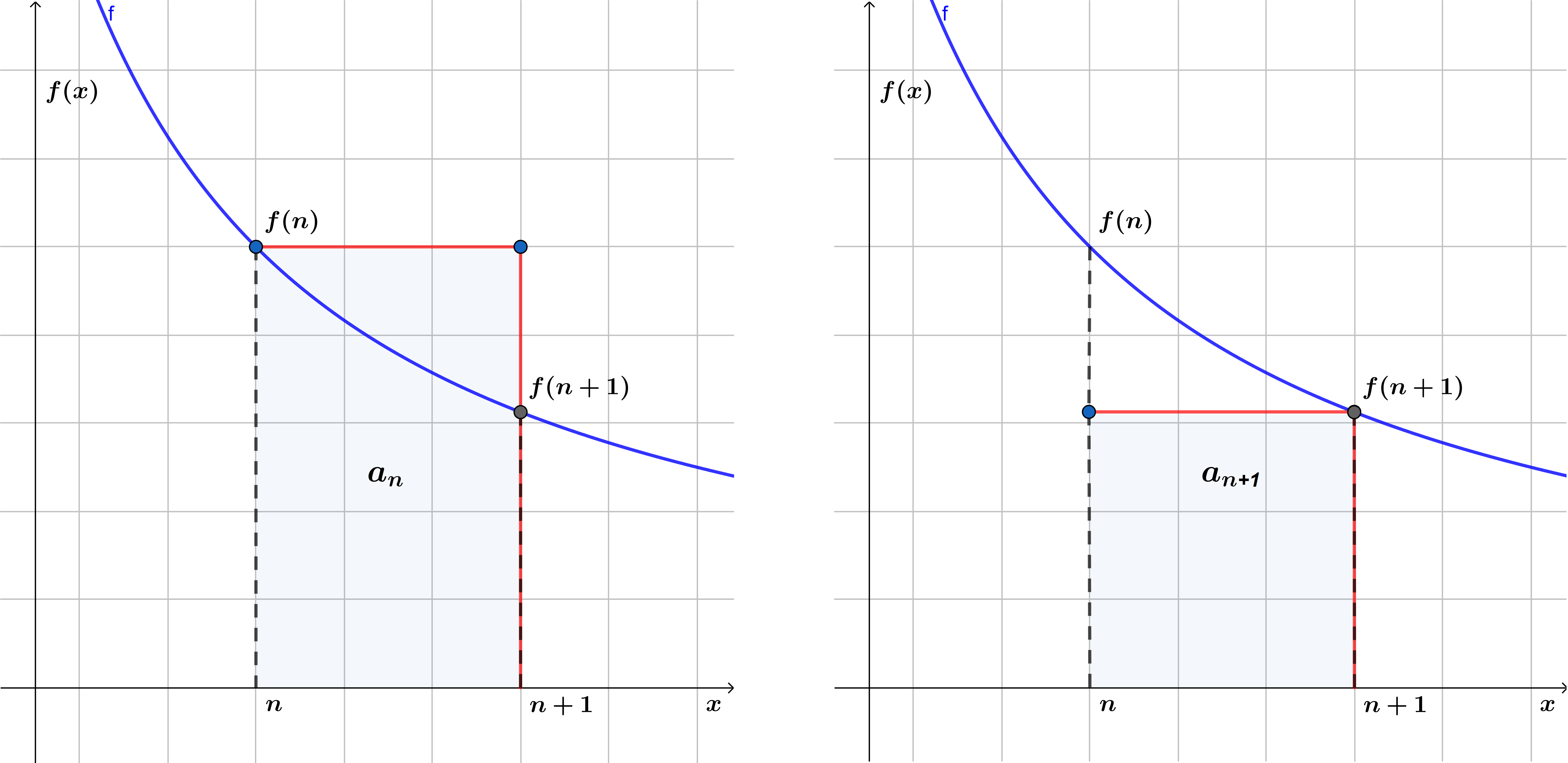
De la figura $(1)$ vemos que el área del rectángulo con altura $f(n)$ (figura de la izquierda) es mayor que el área bajo la curva entre $n$ y $n+1$, en donde se interpretan a estos rectángulos como el área del valor n-esimo de la sucesión $a_n$.

Matemáticamente, podemos interpretar lo anterior como:

$$\Rightarrow a_n\ge {\int }_n^{n+1}f(x)dx$$

Si hacemos lo anterior para $n$ rectángulos, se tiene que:

$$\Rightarrow \sum _{i=1}^n{a}_i\ge \sum _{i=1}^n{\int }_n^{n+1}f(x)$$

$$\Rightarrow \sum _{i=1}^n{a}_i\ge {\int }_1^{2}f(x)d+{\int }_2^{3}f(x)+\dots +{\int }_n^{n+1}f(x)dx$$

$$\Rightarrow \sum _{i=1}^n{a}_i\ge {\int }_1^{n+1}f(x)dx$$

$$\Rightarrow \underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n{a}_i\ge \underset{n\to \mathrm{\infty }}{lim}{\int }_1^{n+1}f(x)dx$$

$$\Rightarrow \sum _{i=1}^{\mathrm{\infty }}{a}_n\ge {\int }_1^{\mathrm{\infty }}f(x)dx$$

Como $\sum _{i=1}^{\mathrm{\infty }}{a}_n$ converge, por el criterio de comparación:

$$\Rightarrow {\int }_1^{\mathrm{\infty }}f(x)dxconverge$$

$\Leftarrow ⌟$

Supongamos que ${\int }_1^{\mathrm{\infty }}f(x)dxconverge$.

De la figura $(1)$ vemos que el área del rectángulo con altura $f(n+1)$ (figura de la derecha) es menor que el área bajo la curva entre $n$ y $n+1$, vemos en este caso que la sucesión correspondiente es $a_{n+1}$.

$$\Rightarrow a_{n+1}\le {\int }_n^{n+1}f(x)dx$$

$$\Rightarrow \sum _{i=1}^{n+1}{a}_i\le {\int }_1^{2}f(x)dx+{\int }_2^{3}f(x)+\dots +{\int }_n^{n+1}f(x)dx$$

$$\Rightarrow \sum _{i=1}^{n+1}{a}_i\le {\int }_1^{n+1}f(x)dx$$

$$\Rightarrow \underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^{n+1}{a}_i\le \underset{n\to \mathrm{\infty }}{lim}{\int }_1^{n+1}f(x)dx$$ $$\Rightarrow \sum _{i=1}^{\mathrm{\infty }}{a}_n\le {\int }_1^{\mathrm{\infty }}f(x)dx$$

Como ${\int }_1^{\mathrm{\infty }}f(x)dx$ converge, por el criterio de comparación

$$\Rightarrow \sum _{i=1}^{\mathrm{\infty }}{a}_{n}converge$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Veamos unos ejemplos:

Ejemplos

Diga si las siguientes series convergen o divergen.

• $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}$$

Tomemos $f(x)=\frac{1}{x}$, sabemos que la función es continua en el intervalo $[1,\mathrm{\infty })$ y es decreciente, además de que sabemos que es continua, por lo que podemos utilizar el criterio de la integral como sigue:

$${\int }_1^{\mathrm{\infty }}\frac{1}{x}dx=\underset{x\to \mathrm{\infty }}{lim}{\int }_1^x\frac{1}{t}dt=\underset{x\to \mathrm{\infty }}{lim}[ln(t)]{|}_1^x=\underset{x\to \mathrm{\infty }}{lim}(ln(x)-ln(1))=\underset{n\to \mathrm{\infty }}{lim}ln(x)=\mathrm{\infty }$$

$$\therefore {\int }_1^{\mathrm{\infty }}\frac{1}{x}dxdiverge$$

$$\therefore \sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}diverge$$

• $$\sum _{i=1}^{\mathrm{\infty }}\frac{n}{n^2+1}$$

Tomamos $f(x)=\frac{x}{x^2+1}$

Claramente, $f$ es continua en $\mathbb{R}\Rightarrow f$ es continua en $[1,\mathrm{\infty })$, vemos que:

$$x^2+1>0\mathrm{\forall }xϵ\mathbb{R}yx>0\Rightarrow xϵ[1,\mathrm{\infty })$$

$$\therefore \frac{x}{x^2+1}>0$$

Veamos si $f(x)$ es decreciente, para ello derivamos:

$$f^{\prime }(x)=\frac{x^2+1-2x^2}{(x^2+1{)}^2}=\frac{-x^2+1}{(x^2+1{)}^2}$$

Vemos que $(x^2+1{)}^2>0$ y si $xϵ[1,\mathrm{\infty })$, entonces $x^2+1>0$, pero tenemos un signo negativo en $f^{\prime }(x)$:

$\therefore f$ es decreciente en $[1,\mathrm{\infty })$.

Por lo que podemos utilizar el criterio de la integral como sigue:

$$\Rightarrow {\int }_1^{\mathrm{\infty }}\frac{x}{x^2+1}dx=\underset{n\to \mathrm{\infty }}{lim}{\int }_1^t\frac{t}{t^2+1}dt=\underset{n\to \mathrm{\infty }}{lim}[\frac{1}{2}ln(t^2+1)]{|}_1^x=\underset{n\to \mathrm{\infty }}{lim}[\frac{1}{2}ln(x^2+1)-\frac{1}{2}ln(2)]=\mathrm{\infty }$$

$$\therefore \sum _{n=1}^{\mathrm{\infty }}\frac{n}{n^2+1}divergea\mathrm{\infty }$$

• $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2+1}$$

Sea $f(x)=\frac{1}{x^2+1}$ Claramente $f$ es continua, positiva y decreciente en $[1,\mathrm{\infty })$, por lo que podemos aplicar el teorema:

$${\int }_1^{\mathrm{\infty }}\frac{1}{x^2+1}dx=\underset{n\to \mathrm{\infty }}{lim}{\int }_1^x\frac{1}{t^2+1}dt=\underset{n\to \mathrm{\infty }}{lim}[\arctan (t)]{|}_1^x=\underset{n\to \mathrm{\infty }}{lim}(\arctan (x)-\arctan (1))=\frac{\pi }{2}-\frac{\pi }{4}=\frac{\pi }{4}$$

$$\therefore {\int }_1^{\mathrm{\infty }}\frac{1}{x^2+1}converge$$

$$\therefore \sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2+1}converge$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

Diga si la siguientes series convergen o divergen.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. $$\sum _{n=1}^{\mathrm{\infty }}\arctan (n)$$
2. $$\sum _{n=1}^{\mathrm{\infty }}\frac{ln(n)}{n}$$
3. $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^3}$$
4. $$\sum _{n=1}^{\mathrm{\infty }}\frac{e^{\frac{1}{n}}}{n^2}$$
5. $$\sum _{n=1}^{\mathrm{\infty }}\frac{2^n}{3^n}$$

Más adelante…

En esta sección vimos el criterio de la integral en el cual se toma como función $f(x)$ a la sucesión $\left\{a_n\right\}$ de la serie, esta función tiene que ser continua, decreciente y positiva en el intervalo $[1,\mathrm{\infty })$ para utilizar este criterio de la integral y observar la convergencia o divergencia de la serie, en la siguiente sección veremos otras series especiales llamadas p-series.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso: Cálculo Diferencial e Integral II: Criterio de la razón y el criterio de la raíz – El blog de Leo (nekomath.com)
• Siguiente entrada del curso: Cálculo Diferencial e Integral II: P-Series – El blog de Leo (nekomath.com)