Introducción

Hasta este punto nos hemos enfocado en estudiar la derivada para distintos tipos de funciones, orientando los esfuerzos principalmente en la ejecución, en derivar tal cual. En esta entrada estudiaremos dos teoremas que nos darán visibilidad de algunas propiedades que tienen las funciones que son derivables en un intervalo abierto.

Teorema de Rolle

En el bachillerato revisaste el tema de máximos y mínimos, donde uno de los criterios que se usaban para encontrarlos era usar el hecho de que si $x_0$ es un mínimo o máximo local, entonces la derivada en dicho punto es cero. De momento, formalizaremos tanto la definición de máximo y mínimo local, así como el criterio de la derivada antes mencionado. Sin embargo, será en una entrada de la siguiente unidad donde daremos la demostración del criterio de la derivada, esto con la finalidad de revisarlo junto con sus aplicaciones.

Definición: Consideremos una función $f$ continua en un intervalo $I$ y $x_0\in (x_0-r,x_0+r)\subset I$ con $r>0$ tal que $f^{\prime }(x_0)$ existe. Decimos que:

• $x_0$ es un máximo local de $f\iff$ existe $r>0$ tal que para todo $x\in (x_0-r,x_0+r)$ ocurre que:
  $$f(x)\le f(x_0).$$
• $x_0$ es un mínimo local de $f\iff$ existe $r>0$ tal que para todo $x\in (x_0-r,x_0+r)$ ocurre que:
  $$f(x_0)\le f(x).$$

Teorema: Consideremos una función $f$ continua en un intervalo $I$ que es derivable en el punto $x_0\in (x_0-r,x_0+r)\subset I$. Si tenemos que $x_0$ es un máximo o un mínimo local de $f$, entonces $f^{\prime }(x_0)=0.$

Ahora veremos el Teorema de Rolle que menciona que si tenemos una función $f:[a,b]\to \mathbb{R}$ continua en $[a,b]$ y derivable en el intervalo $(a,b)$, que satisface que $f(a)=f(b)$, entonces existe un punto $c$ cuya derivada es cero, es decir, si la función inicia y termina en el mismo punto, entonces existe al menos un máximo o un mínimo local.

Teorema de Rolle. Sea $f:[a,b]\to \mathbb{R}$ tal que $f$ es continua en $[a,b]$ y derivable en $(a,b)$. Si $f(a)=f(b)$, entonces existe $c$, $a<c<b$ tal que $f^{\prime }(c)=0.$

Demostración.

Caso 1: Para todo $x\in [a,b]$, $f(x)=k.$

Como $f$ es constante, entonces $f^{\prime }(x)=0$ para todo $x\in [a,b].$

Así, podemos considerar $c=\frac{a+b}{2}$. Donde se cumple que $a<c<b$ y $f^{\prime }(c)=0.$

Caso 2: Existe $x_0\in [a,b]$, tal que $f(x_0)>f(a).$

Por el teorema del máximo-mínimo, existe $c\in [a,b]$ tal que para todo $x\in [a,b]$ se tiene que $f(x)\le f(c).$ Entonces,

$$\begin{array}{c}f(a)<f(x_0)\le f(c).\end{array}$$

Se sigue que
$$\begin{array}{cc}& f(c)>f(a)=f(b).\\ \\ \therefore & c\ne a,c\ne b.\\ \\ \therefore & c\in (a,b),a<c<b.\end{array}$$

Por tanto, para todo $x\in [a,b]$, se cumple que $f(x)\le f(c)$. Donde se concluye que $f$ es un máximo local en $c.$

Además, $f$ es derivable en $(a,b)$. Por tanto, es derivable en $c$. Por el teorema anterior, se concluye que $f^{\prime }(c)=0.$

Caso 3: Existe $x_0\in [a,b]$ tal que $f(x_0)<f(a)$.

Este caso es análogo al anterior.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Teorema del Valor Medio

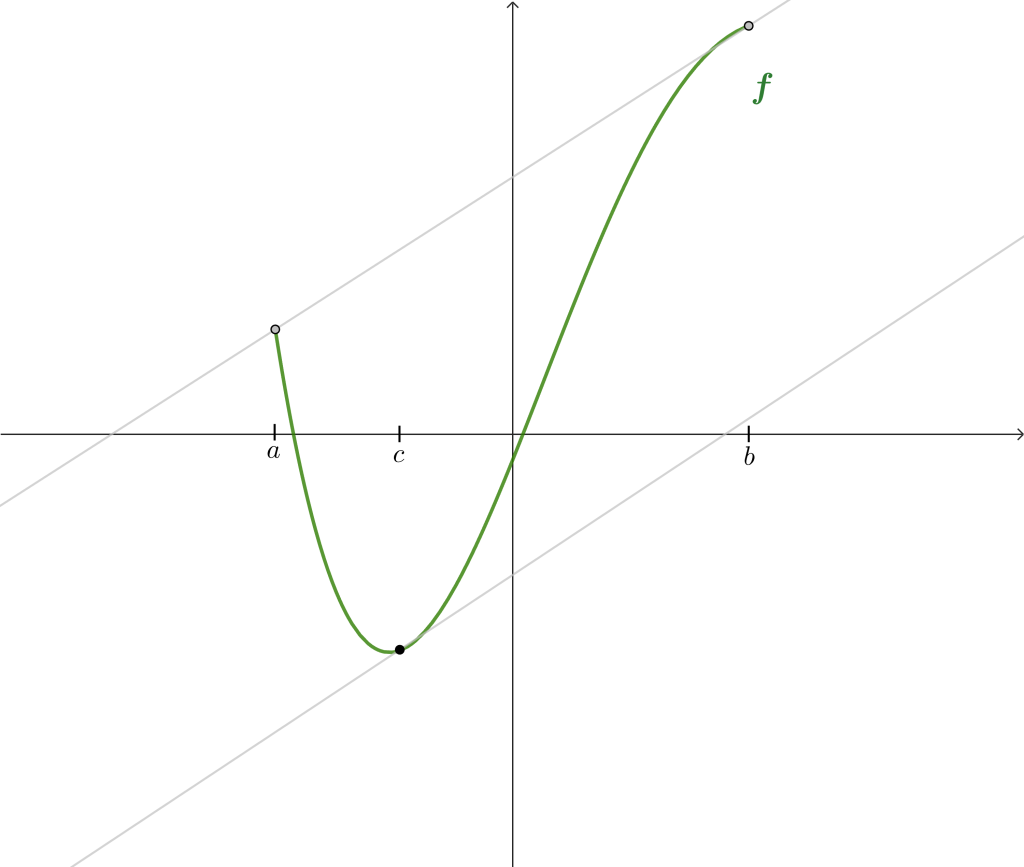
El siguiente teorema que probaremos indica que si una función es continua en $[a,b]$ y derivable en el intervalo $(a,b)$, entonces existe un punto $c$ cuya derivada es $$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}.$$

Lo anterior indica que existe un punto $c$ de tal manera que la pendiente de la recta tangente es la misma que la pendiente de la recta que pasa por los puntos extremos del intervalo $a$, $b$. Esto se puede ver gráficamente en la siguiente imagen.

Teorema del Valor Medio. Sea $f:[a,b]\to \mathbb{R}$ continua en $[a,b]$, derivable en $(a,b)$, entonces existe $c$, $a<c<b$ tal que

$$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}.$$

Demostración.

Consideremos $g(x)=f(a)+\left(\frac{f(b)-f(a)}{b-a}\right)(x-a)$ y $\rho (x)=f(x)-g(x)$. Así, se tiene que

$$\rho (x)=f(x)–(f(a)+\left(\frac{f(b)-f(a)}{b-a}\right)(x-a)).$$

Notemos que $\rho :[a,b]\to \mathbb{R}$, cumple que

1. $\rho$ es continua en $[a,b]$ pues $f$ lo es.
2. $\rho$ es derivable en $(a,b)$ pues $f$ lo es.
3. $\rho (a)=f(a)-(f(a)+0)=0$ y $\rho (b)=f(b)-(f(a)+f(b)-f(a))=0$. Por tanto, $\rho (a)=\rho (b)$.

Por el teorema de Rolle, existe $c$, $a<c<b$ tal que ${\rho }^{\prime }(c)=0$. Veamos que

$$\begin{array}{rl}{\rho }^{\prime }(x)& =f^{\prime }(x)-{((f(a)+\frac{f(b)-f(a)}{b-a})(x-a))}^{\prime }\\ \\ & =f^{\prime }(x)-(0+\frac{f(b)-f(a)}{b-a}(1))\\ \\ & =f^{\prime }(x)–\left(\frac{f(b)-f(a)}{b-a}\right).\end{array}$$

$$\therefore {\rho }^{\prime }(x)=f^{\prime }(x)–\left(\frac{f(b)-f(a)}{b-a}\right).$$

Considerando que ${\rho }^{\prime }(c)=0$, de la expresión anterior, se sigue que

$$f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Corolario. Si para todo $x\in (a,b)$, $f^{\prime }(x)=0$, entonces existe $k\in \mathbb{R}$ tal que $\mathrm{\forall }x\in [a,b]$ se tiene que $f(x)=k.$

Demostración.

Si $x=a$, entonces $f(x)=f(a)$. Si $x\in [a,b]$, con $x\ne a$, entonces $x>a$. Aplicando el Teorema del Valor Medio en $[a,x]$, existe $c$, $a<c<x\le b$ tal que

$$f^{\prime }(c)=\frac{f(x)-f(a)}{x-a}.$$

Por hipótesis, $f^{\prime }(c)=0$ y $x\ne a$, entonces

$$\begin{array}{cc}& 0=\frac{f(x)-f(a)}{x-a}.\\ \\ \iff & f(x)-f(a)=0.\\ \\ \iff & f(x)=f(a).\end{array}$$

Por tanto, para todo $x\in [a,b]$, se tiene que $f(x)=k$, con $k=f(a).$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Corolario. Sean $f,g:[a,b]\to \mathbb{R}$ continuas en $[a,b]$ y derivables en $(a,b)$. Si para todo $x\in (a,b)$, $f^{\prime }(x)=g^{\prime }(x)$, entonces $f(x)=g(x)+k.$

Demostración.

Consideremos $h(x)=f(x)-g(x)$, entonces se tiene que $h^{\prime }(x)=f^{\prime }(x)-g^{\prime }(x)=0$ para todo $x\in (a,b).$

Por el corolario anterior, existe $k\in \mathbb{R}$, constante, tal que para todo $x\in [a,b]$ se tiene $h(x)=k.$ Se sigue que

$$\begin{array}{cc}& f(x)-g(x)=k.\\ \therefore & f(x)=g(x)+k\mathrm{\forall }x\in [a,b].\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más adelante…

La siguiente entrada será la última de la unidad y revisaremos un potente resultado de la derivada que nos permitirá hacer el cálculo de cierto tipo de límites con mayor facilidad, este resultado es conocido como la regla de L’Hôpital.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

• Comprueba el teorema de Rolle en los intervalos que se muestran y halla los valores de $c$ para las siguientes funciones:
  • $f(x)=x^2-x-6$ en el intervalo $[-2,3].$
  • $f(x)=x^2-4$ en el intervalo $[-2,2].$
  • $f(x)=\sqrt{x}-2\sqrt[4]{x}$ en el intervalo $[0,16].$
• Comprueba el teorema del valor medio en los intervalos que se muestran y encuentra el valor $c$ para las siguientes funciones:
  • $f(x)=\sqrt{x+1}$ en el intervalo $[-1,3].$
  • $f(x)=sen(x)$ en el intervalo $[0,\pi /4].$
  • $f(x)=ln(2x+5)$ en el intervalo $[0,2].$

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral I
• Entrada anterior del curso: Derivadas implícitas y de orden superior
• Siguiente entrada del curso: La regla de L’Hôpital
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»