Introducción

Antes de comenzar con el estudio de los métodos de integración veremos en esta sección un tema importante que es la definición de antiderivadas.

La antiderivada o función primitiva de una función $f(x)$ es una función $F(x)$ tal que al ser derivada nos generará la misma función $f(x)$. Por lo que, $F(x)$ es una antiderivada de $f(x)$ si $F^{\prime }(x)=f(x)$.

En notación integral se expresa como:

$$\int f(x)dx=F(x)$$

Antiderivada

Definimos la antiderivada de una función como sigue.

Definición. Una función $F(x)$ es una antiderivada de $f(x)$ si $F^{\prime }(x)=f(x)$, En notación integral:

$$\int f(x)dx=F(x)+C$$

Donde $C$ es la constante de integración.

Observación: Dada una función $f(x)$, la antiderivada no es única, puesto que existe una infinidad de antiderivadas o una familia de antiderivadas, es decir, si $F(x)$ es una antiderivada de $f(x)$ entonces $F(x)+C$ es una antiderivada de $f(x)$.

Veamos el siguiente teorema:

Teorema: Si $F(x)$ es una antiderivada de $f(x)$ en un intervalo $I$, es decir, en un intervalo abierto o cerrado, entonces la función $G(x)$ es una antiderivada de $f(x)$ $\iff G(x)=F(x)+C$, $$$\mathrm{\forall }$ $x$ $ϵ$ $I$

Demostración:

$\Rightarrow$ $\rfloor$

Por hipótesis $F(x)$ y $G(x)$ son antiderivadas de $f(x)$, entonces por definición:

$$F^{\prime }(x)=f(x)y{G}^{\prime }(x)=f(x)\Rightarrow F^{\prime }(x)=G^{\prime }(x)$$

Por el colorario visto en el curso de Cálculo I en el tema de Teorema de Rolle y Teorema del Valor Medio, tenemos que:

$$G(x)=F(x)+C$$

$\Leftarrow$ $\rfloor$

Tenemos que $G(x)=F(x)+C$, derivando la relación anterior tenemos que:

$$\frac{\mathrm{d}}{\mathrm{d}x}(G(x))=\frac{\mathrm{d}}{\mathrm{d}x}(F(x)+C)$$

Como $F(x)$ es una antiderivada de $f(x)$ entonces $F^{\prime }(x)=f(x)$

$\Rightarrow G^{\prime }(x)=f(x)$ Justo lo que buscamos, ya que recordemos que es la definición de una antiderivada.

$\therefore$ $G(x)$ es una antiderivada de $f(x)$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Para entender un poco mejor el concepto de la familia de antiderivadas veamos el ejemplo siguiente:

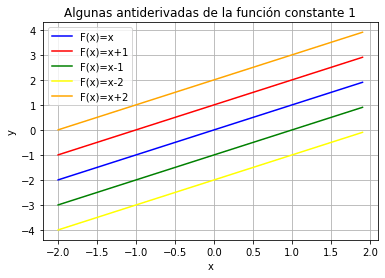
Sea $F(x)=x$, que es la antiderivada de la función constante $f(x)=1$, ya que $F^{\prime }(x)=1=f(x)$. En notación de integral:

$$\int 1dx=x+c$$

En la siguiente imagen (figura 1) se muestran algunas antiderivadas de la función constante $f(x)=1$, donde el valor de la constante va cambiando en cada función de la gráfica y es por eso que existe una infinidad de antiderivadas de una función. Ahí la importancia de escribir la constante de integración cuando se resuelva una integral indefinida.

Nota: Una integral definida de una función $f(x)$ dentro de un intervalo $I$ entre $a$ y $b$, nos da un resultado numérico, es decir:

$${\int }_a^{b}f(x)dx=C$$

En cambio, una antiderivada nos da un conjunto de familia de funciones, es decir:

$$\int f(x)dx=F(x)+C$$

Algunas antiderivadas básicas

En la siguiente tabla se muestran algunas derivadas e integrales indefinidas básicas necesarias que nos serán útiles para comenzar a estudiar los métodos de integración y que nos ayudará con algunos ejercicios y ejemplos en las siguientes secciones.

Derivada	Integral indefinida
$$\frac{\mathrm{d}}{\mathrm{d}x}C=0$$	$$\int 0dx=C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}x=1$$	$$\int 1dx=x+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(x^n)=n{x}^{n-1}$$	$$\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$$ $\mathrm{\forall }$ $n$ $\ne$ $-1$
$$\frac{\mathrm{d}}{\mathrm{d}x}(\sin (x))=\cos (x)$$	$$\int \cos (x)dx=\sin (x)+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(\cos (x))=-\sin (x)$$	$$\int \sin (x)dx=-\cos (x)+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(\tan (x))={\sec }^2(x)$$	$$\int {\sec }^2(x)dx=\tan (x)+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(\cot (x))=-{\csc }^2(x)$$	$$\int {\csc }^2(x)dx=-\cot (x)+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(\sec (x))=-\sec (x)\tan (x)$$	$$\int \sec (x)\tan (x)dx=\sec (x)+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(\csc (x))=-\csc (x)\cot (x)$$	$$\int \csc (x)\cot (x)dx=-\csc (x)+C$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(f(x)+g(x))=\frac{\mathrm{d}}{\mathrm{d}x}(f(x))+\frac{\mathrm{d}}{\mathrm{d}x}(g(x))$$	$$\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx$$
$$\frac{\mathrm{d}}{\mathrm{d}x}(Cf(x))=C\frac{\mathrm{d}}{\mathrm{d}x}(f(x))$$	$$\int [Cf(x)]dx=C\int f(x)dx$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para practicar lo aprendido y que te ayudarán en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

Resuelve las siguientes integrales:

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. $$\int \frac{1}{x^2}dx$$
2. $$\int \sqrt{x}dx$$
3. $$\int 2\sin (x)dx$$
4. $$\int 100dx$$
5. $$\int (x+2)dx$$
6. $$\int \frac{x+1}{\sqrt{x}}dx$$

Más adelante…

En esta sección vimos la definición de antiderivada o también conocido como función primitiva $f(x)$, además de, algunas integrales indefinidas básicas que necesitaremos para estudiar los métodos de integración. Como primer método de integración que estudiaremos en la siguiente sección es el método de cambio de variable o integración por sustitución.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso:
• Siguiente entrada del curso: Cálculo Diferencial e Integral II: Método de sustitución o cambio de variable – El blog de Leo (nekomath.com)