Introducción
Alternativamente a la definición épsilon-delta revisada en la entrada anterior, se puede estudiar el límite de una función a través de límites de sucesiones; este enfoque tiene varias bondades en el sentido de que podremos hacer un amplio uso de las propiedades demostradas anteriormente para el límite de una sucesión. En esta entrada nos enfocaremos en probar un teorema que nos indica la equivalencia entre ambas formas de concebir el límite de una función.
Negación de la definición del límite de una función
Veamos primero qué significa que el límite de una función no exista, es decir, revisaremos la negación del concepto dado en la entrada anterior, para ello retomemos la definición de límite de una función:
Definición. Decimos que $f$ tiende hacia el límite $L$ en $x_0$ si para todo $\varepsilon > 0$ existe algún $\delta > 0$ tal que, para todo $x$, si $0<|x-x_0|< \delta$, entonces $|f(x)-L|< \varepsilon.$
De esta forma, si no se cumple la definición anterior, entonces tenemos lo siguiente: $f$ no tiende hacia el límite $L$ en $x_0$ si existe algún $\varepsilon > 0$, tal que para todo $\delta > 0$, hay algún $x$ que satisface $0 < |x-x_0| < \delta$, pero $|f(x)-L| \geq \varepsilon.$
Criterio de sucesiones para límites
Es momento de revisar un teorema que será particularmente útil para demostrar las propiedades del límite de una función. Este teorema nos indica que una función $f$ tiende al límite $L$ en $x_0$ si y solo si para toda sucesión $\{ a_n \}$ en el dominio de $f$ que converja a $x_0$ se tiene que la sucesión generada por $\{f(a_n) \}$ converge a $L.$
Teorema. Sean $A \subset \mathbb{R}$, $f:A \rightarrow \mathbb{R}$ y $x_0$ un punto de acumulación de $A$. Los siguientes enunciados son equivalentes.
- $$\lim_{x \to x_0} f(x) = L.$$
- Para toda sucesión $\{ a_n \}$ en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$, la sucesión $\{f(a_n)\}$ converge a $L.$
Demostración.
$1) \Rightarrow 2)]$ Sea $\varepsilon >0$. Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Y sea $\{ a_n \}$ una sucesión en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$.
Por hipótesis $f$ converge a $L$ en $x_0$, entonces existe $\delta > 0$ tal que si
$0<|x-x_0|<\delta$, entonces $|f(x)-L| < \varepsilon.$
Además, como la sucesión $\{a_n\}$ converge a $x_0$, para el valor $\delta > 0$ dado, existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ entonces $0<|a_n- x_0| < \delta$ y por hipótesis de la convergencia de $f$ a $L$ en $x_0$, podemos concluir que $|f(a_n)-L| < \varepsilon$. Así la sucesión $\{f(a_n)\}$ converge a $L$, es decir,
$$\lim_{n \to \infty} f(a_n) = L.$$
$1) \Leftarrow 2)]$ Procederemos a hacer esta implicación por contrapositiva, es decir, demostraremos que si no sucede $1)$, entonces tampoco sucede $2).$
Supongamos que $1)$ no se cumple, es decir, existe algún $\varepsilon_0 > 0$, tal que para todo $\delta > 0$, hay al menos un real $x$ que cumple $0<|x-x_0| < \delta$, pero $|f(x)-L| \geq \varepsilon_0$. Así, consideremos justo ese valor de $\varepsilon_0.$ Notemos que para todo natural $n \in \mathbb{N}$, si consideramos $\delta=\frac{1}{n}$, entonces existe al menos un término $a_n$ en $A$ tal que $0<|a_n-x_0| < \frac{1}{n}$, pero $|f(a_n)-L| \geq \varepsilon_0.$
Tomemos la sucesión generada por $\{a_n\}$, se tiene que la sucesión $\{ a_n \}$ converge a $x_0$ y $a_n \neq x_0$ para todo $n \in \mathbb{N}$, pero la sucesión $\{f(a_n)\}$ no converge a $L$. Así, si no se cumple $1)$, entonces tampoco $2)$. Por lo anterior, podemos concluir que $2) \Rightarrow 1).$
$\square$
Límite de una función a través de sucesiones
Ahora nos enfocaremos en hacer uso del teorema anterior. En el momento de hacer las demostraciones correspondientes, debemos tener presente que una vez que expresamos el límite de una función en términos del límite de una sucesión, podemos hacer uso de las propiedades del mismo.
Ejemplo 1. Sea $A =\mathbb{R} \backslash \{ 1 \}$. Consideremos la función $f: A \to \mathbb{R}$ con $f(x) = \frac{x^3-x^2+x-1}{x-1}$. Prueba que $$\lim_{x \to 1} f(x) = 2.$$
Demostración.
Primero notemos que
\begin{align*}
f(x) & = \frac{x^3-x^2+x-1}{x-1} \\ \\
& = \frac{(x-1)(x^2+1)}{x-1} \\ \\
& = x^2+1.
\end{align*}
$$\therefore f(x) = x^2+1.$$
Sea $\{a_n\}$ una sucesión en $\mathbb{R}$ tal que
- $\lim\limits_{n \to \infty} a_n = 1.$
- Para todo $n \in \mathbb{N}$, $a_n \neq 1.$
- Para todo $n \in \mathbb{N}$, $a_n \in A.$
Entonces tenemos que
\begin{align*}
\lim_{x \to 1} f(x) & = \lim_{n \to \infty} f(a_n) \\ \\
& = \lim_{n \to \infty} (a_n^2+1) \\ \\
& = \lim_{n \to \infty} a_n^2 + \lim_{n \to \infty} 1 \tag{1} \\ \\
& = 1+1 \\ \\
& = 2.
\end{align*}
$$\therefore \lim_{x \to 1} \frac{x^3-x^2+x-1}{x-1} = 2.$$
$\square$
Es importante resaltar que aún no hemos probado ninguna propiedad del límite de una función, por lo que el criterio de sucesiones para límites es lo que nos permite emplear las propiedades que conocemos respecto a sus operaciones aritméticas y así realizar el paso $(1)$ en el ejemplo anterior.
Ejemplo 2. Sea $A = [0, \infty)$. Consideremos la función $f: A \to \mathbb{R}$ con $f (x) = \sqrt{x}$. Demuestra que $$\lim_{x \to 2} f(x) = \sqrt{2}.$$
Sea $\{a_n\}$ una sucesión en $\mathbb{R}$ tal que
- $\lim\limits_{n \to \infty} a_n = 2.$
- Para todo $n \in \mathbb{N}$, $a_n \neq 2.$
- Para todo $n \in \mathbb{N}$, $a_n \in A.$
Sabemos que si $\{a_n\}$ converge a $2$, entonces $\{ \sqrt{a_n} \}$ converge a $\sqrt{2}$. Así, tenemos que
\begin{align*}
\lim_{x \to 2} f(x) & = \lim_{n \to \infty} f(a_n) \\
& = \lim_{n \to \infty} \sqrt{a_n} \\
& = \sqrt{2}.
\end{align*}
$$\therefore \lim_{x \to 2} \sqrt{x} = \sqrt{2}.$$
$\square$
Ejemplo 3. Sea $A =\mathbb{R} \backslash \{ 0 \}$. Consideremos la función $f: A \to \mathbb{R}$ con $f (x)= \frac{(3+x)^2-9}{x}$. Prueba que $$\lim_{x \to 0} f(x) = 6.$$
Demostración.
Primero notemos que
\begin{align*}
f (x) & = \frac{(3+x)^2-9}{x} \\ \\
& = \frac{9+6 x+x^2-9}{x} \\ \\
& = \frac{6x+x^2}{x} \\ \\
& = 6+x.
\end{align*}
$$\therefore f(x) = 6+x.$$
Sea $\{a_n\}$ una sucesión en $\mathbb{R}$ tal que
- $\lim\limits_{n \to \infty} a_n = 0.$
- Para todo $n \in \mathbb{N}$, $a_n \neq 0.$
- Para todo $n \in \mathbb{N}$, $a_n \in A.$
\begin{align*}
\lim_{x \to 0} f(x) & = \lim_{n \to \infty} f(a_n) \\ \\
& = \lim_{n \to \infty} (6+a_n) \\ \\
& = 6.
\end{align*}
$$\therefore \lim_{x \to 0} \frac{(3+x)^2-9}{x} = 6.$$
$\square$
Hasta este momento, solo hemos hecho uso del criterio de sucesiones para límites para probar la existencia de los mismos. Sin embargo, es posible usarlo también para el caso en el que tal límite no existe. Derivado directamente del teorema anterior se tiene que:
- Si existen dos sucesiones $\{ a_n \}$, $\{b_n\}$ en el dominio de $f$, ambas convergentes a $x_0$, tal que $a_n$, $b_n \neq x_0$ para todo $n \in \mathbb{N}$, pero $\lim\limits_{n \to \infty} f(a_n) \neq \lim\limits_{n \to \infty} f(b_n)$ entonces no existe el límite de $f$ en $x_0.$
Veremos ahora un ejemplo donde el límite no existe.
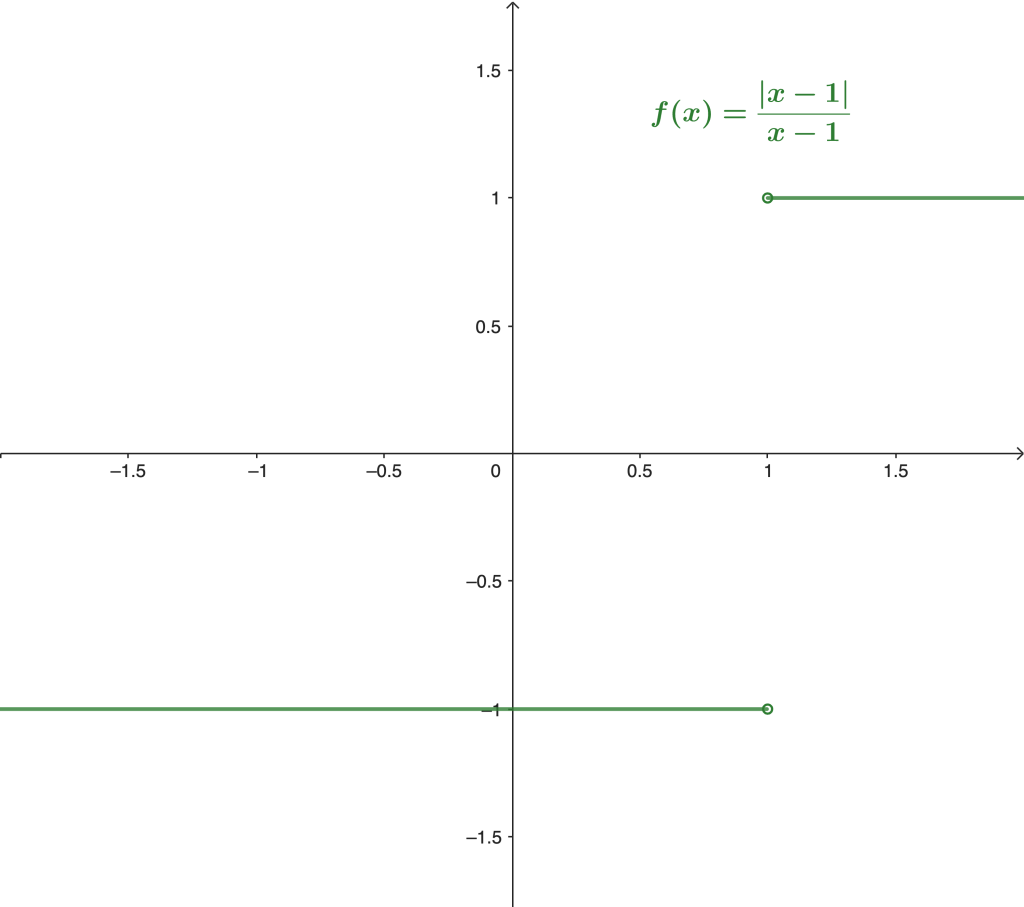
Ejemplo 4. Sea $A =\mathbb{R} \backslash \{ 1 \}$. Consideremos la función $f: A \to \mathbb{R}$ con $f(x) = \frac{|x-1|}{x-1}$. Prueba que el límite
$$\lim_{x \to 1} f(x)$$
no existe.
Demostración.
Veamos primero la gráfica de la función:
Podemos observar que es conveniente tomar una sucesión que se aproxime a $x_0 = 1$ por la derecha y otra que se aproxime por la izquierda. Sean $\{a_n\}$, $\{b_n\}$ dos sucesiones en el dominio de $f$ definidas de la siguiente forma:
$$a_n = 1 + \frac{1}{n} \quad \text{y} \quad b_n = 1 – \frac{1}{n}.$$
Se sigue que
$$ \lim_{n \to \infty} a_n = 1 \quad \text{y} \quad \lim_{n \to \infty} b_n = 1.$$
Además, $a_n \neq 1$, $b_n \neq 1$ para todo $n \in \mathbb{N}$.
Se tiene que
\begin{align*}
\lim_{n \to \infty} f(a_n) & = \lim_{n \to \infty} \frac{|a_n-1|}{a_n-1} \\ \\
& = \lim_{n \to \infty} \frac{ |1 + \frac{1}{n} – 1|}{1 + \frac{1}{n} -1} \\ \\
& = \lim_{n \to \infty} \frac{ |\frac{1}{n}|}{ \frac{1}{n} } \\ \\
& = \lim_{n \to \infty} \frac{ \frac{1}{n} }{ \frac{1}{n} } \\ \\
& = 1.
\end{align*}
$$\therefore \lim_{n \to \infty} f(a_n) = 1 \tag{1}.$$
Por otro lado,
\begin{align*}
\lim_{n \to \infty} f(b_n) & = \lim_{n \to \infty} \frac{|b_n-1|}{b_n-1} \\ \\
& = \lim_{n \to \infty} \frac{ |1 – \frac{1}{n} – 1|}{1 – \frac{1}{n} -1} \\ \\
& = \lim_{n \to \infty} \frac{ |- \frac{1}{n}|}{- \frac{1}{n} } \\ \\
& = \lim_{n \to \infty} \frac{ \frac{1}{n} }{ – \frac{1}{n} } \\ \\
& = – 1.
\end{align*}
$$\therefore \lim_{n \to \infty} f(b_n) = -1. \tag{2}$$
De $(1)$ y $(2)$, se tiene que
\begin{gather*}
\lim_{n \to \infty} f(a_n) \neq \lim_{n \to \infty} f(b_n). \\ \\
\therefore \lim_{x \to 1} \frac{|x-1|}{x-1} \text{ no existe.}
\end{gather*}
$\square$
Más adelante…
En las siguientes entradas veremos propiedades específicas que nos ayudarán a calcular el límite de una función; y, como podrás imaginar, varias de estas propiedades son un símil a las revisadas para las sucesiones convergentes.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
A través del criterio de sucesiones para límite, prueba si existen o no los siguientes límites:
- $$\lim_{x \to 0} \frac{x}{x+1}.$$
- $$\lim_{x \to 0} x \cdot |x|.$$
- $$\lim_{x \to 7} \frac{x^2-5x+10}{2-x}.$$
- $$\lim_{x \to 0} \frac{x}{|x|}.$$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Definición formal de límite de una función
- Siguiente entrada del curso: Teoremas sobre el límite de una función
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

No entiendo la segunda parte. ¿Por qué al fijar delta = 1/n ocurre que la imagen del elemento Xn q está dentro de delta =1/n, no converge a L? Osea, por qué para un n€N existe un Xn tal que si 0< |Xn – Xo| < 1/n, ocurre que |f(x) – L| < épsilon?
A ver si puede ayudarme. Gracias.
Hola María. Había por ahí un subíndice mal que ya corregimos, quizás eso ayuda. La idea es usar que la convergencia (1) no se da, y entonces como falla para cualquier delta, entonces nos vamos tomando muchos deltas específicos (1/1, 1/2, 1/3, …, 1/n, …). Cada uno de esos deltas tiene un x que falla. A para delta=1/n le llamamos x_n al x que falla. Esto permite construir la sucesión x_1, x_2, x_3, … que sí converge a x_0, pero para la cual no se da la convergencia de f_(x_n) a L pues justo elegimos los x_i para que la diferencia |f(x_n)-L| siempre fuera mayor que epsilon_0.