Archivo del Autor: Angélica Amellali Mercado Aguilar

El Teorema de la función implícita (parte 2)

Por Angélica Amellali Mercado Aguilar

1 respuesta

Teorema de la Función Implícita (f:R→R

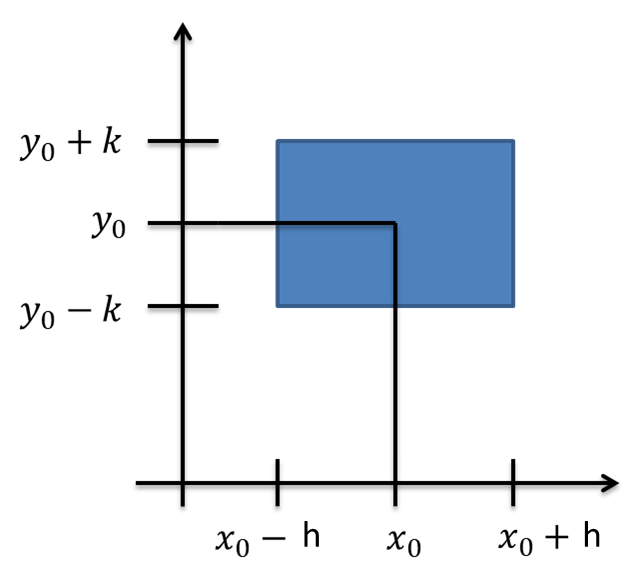
Teorema. Considere la función y=f(x). Sea (x0,y0)∈R2 un punto tal que F(x0,y0)=0. Suponga que la función F tiene derivadas parciales continuas en alguna bola con centro (x0,y0) y que ∂F∂y(x0,y0)≠0. Entonces F(x,y)=0 se puede resolver para y en términos de x y definir así una función y=f(x) con dominio en una vecindad de (x0,y0), tal que y0=f(x0), lo cual tiene derivadas continuas en V que pueden calcularse como y′=f′(x)=∂F∂x(x,y)∂F∂y(x,y), x∈V.

Ejercicio. Si y′=f′(x)=−∂F∂x(x,y)∂F∂y(x,y) calcular y»

Solución. En este caso
y»=−(∂F∂y)[∂2F∂x2dxdx+∂2F∂y∂xdydx]−(∂F∂x)[∂2F∂x∂ydxdx+∂2F∂y2dydx](∂F∂y)2
=−(∂F∂y)[∂2F∂x2+∂2F∂y∂x(−∂F∂x∂F∂y)]−(∂F∂x)[∂2F∂x∂ydxdx+∂2F∂y2(−∂F∂x∂F∂y)](∂F∂y)2
=−(∂F∂y)2(∂2F∂x2)−(∂2F∂y∂x)(∂F∂x)(∂F∂y)−(∂F∂x)(∂F∂y)(∂2F∂x∂y)+(∂F∂x)2(∂2F∂y2)(∂F∂y)3
=−(∂F∂y)2(∂2F∂x2)−2(∂2F∂y∂x)(∂F∂x)(∂F∂y)+(∂F∂x)2(∂2F∂y2)(∂F∂y)3

Teorema de la Función Implícita (f:R2→R)

Teorema. Considere la función F(x,y,z). Sea (x0,y0,z0)∈R3 un punto tal que F(x0,y0,z0)=0. Suponga que la
función F tiene derivadas parciales ∂F∂x, ∂F∂y, ∂F∂z continuas en alguna bola con
centro (x0,y0,z0) y que ∂F∂z(x0,y0,z0)≠0.
Entonces F(x,y,z)=0 se puede resolver para z en términos de x,y
y definir así una función z=f(x,y) con dominio en una vecindad de
(x0,y0,z0), tal que z0=f(x0,y0), lo cual tiene derivadas continuas
en V que pueden calcularse como dzdx(x,y)=−∂F∂x(x,y)∂F∂z(x,y)   dzdy(x,y)=−∂F∂y(x,y)∂F∂z(x,y)

Ejercicio. Si
dzdx(x,y)=−∂F∂x(x,y)∂F∂z(x,y) calcular ∂2F∂x2

Solución. Tenemos que
∂2F∂x2=∂∂x(−∂F∂x(x,y)∂F∂z(x,y))=−(∂F∂z)[∂2F∂x2dxdx+∂2F∂y∂xdydx+∂2F∂z∂xdzdx]−(∂F∂x)[∂2F∂x∂zdxdx+∂2F∂y∂zdydx+∂2F∂z2dzdx](∂F∂z)2
=−(∂F∂z)[∂2F∂x2+∂2F∂z∂xdzdx]−(∂F∂x)[∂2F∂x∂z+∂2F∂z2dzdx](∂F∂z)2
=−(∂F∂z)[∂2F∂x2+∂2F∂z∂x(−∂F∂x∂F∂z)]−(∂F∂x)[∂2F∂x∂z+∂2F∂z2(−∂F∂x∂F∂z)](∂F∂z)2
=−(∂F∂z)2∂2F∂x2−2∂2F∂z∂x∂F∂x∂F∂z+(∂F∂x)2∂2F∂z2(∂F∂z)3

Ejercicio. Si
dzdy(x,y)=−∂F∂y(x,y)∂F∂z(x,y) calcular ∂2F∂y2

Solución. tenemos que
∂2F∂y2=∂∂y(−∂F∂y(x,y)∂F∂z(x,y))=−(∂F∂z)[∂2F∂y∂xdxdy+∂2F∂y2dydy+∂2F∂z∂ydzdy]−(∂F∂y)[∂2F∂x∂zdxdy+∂2F∂y∂zdydy+∂2F∂z2dzdy](∂F∂z)2
=−(∂F∂z)[∂2F∂y2+∂2F∂z∂ydzdy]−(∂F∂y)[∂2F∂y∂z+∂2F∂z2dzdy](∂F∂z)2
=−(∂F∂z)[∂2F∂y2+∂2F∂z∂y(−∂F∂y∂F∂z)]−(∂F∂y)[∂2F∂y∂z+∂2F∂z2(−∂F∂y∂F∂z)](∂F∂z)2
=−(∂F∂z)2∂2F∂y2−2∂2F∂z∂y∂F∂y∂F∂z+(∂F∂y)2∂2F∂z2(∂F∂z)3

Ejercicio. Si
dzdy(x,y)=−∂F∂y∂F∂z calcular ∂2F∂y∂x

Solución. tenemos que
∂2F∂y∂x=∂∂y(∂F∂x)=∂∂y(−∂F∂x∂F∂z)=
−(∂F∂z)[∂2F∂y∂x+∂2F∂z∂x∂z∂y]−(∂F∂x)[∂2F∂y∂z+∂2F∂z2∂z∂y](∂F∂z)2
−(∂F∂z)[∂2F∂y∂x+∂2F∂z∂x(−∂F∂y∂F∂z)]−(∂F∂x)[∂2F∂y∂z+∂2F∂z2(−∂F∂y∂F∂z)](∂F∂z)2
=−(∂F∂z)2∂2F∂y∂x−∂2F∂z∂x∂F∂y∂F∂z−∂2F∂y∂z∂F∂x∂F∂z+∂2F∂z2∂F∂x∂F∂y(∂F∂z)3

Teorema de la Función Implicita (version sistemas de ecuaciones)

Consideremos ahora el sistema

au+bv−k1x=0
cu+dv−k2y=0

con a,b,c,d,k1,k2 constantes. Nos preguntamos cuando
podemos resolver el sistema para u y v en términos de x y y.
Si escribimos el sistema como

au+bv=k1x
cu+dv=k2y

y sabemos que este sistema tiene solución si det|abcd|≠0 en tal caso escribimos

u=1det|abcd|(k1dx−k2by),~~v=1det|abcd|(k2ay−k1cx).

Esta solución no cambiaría si consideramos


au+bv=f1(x,y)
cu+dy=f2(x,y)


donde f1 y f2 son funciones dadas de x y y. La posibilidad de despejar las variables u y v en términos de x y y recae sobre los coeficientes de estas variables en las ecuaciones dadas.

Ahora si consideramos ecuaciones no lineales en u y v escribimos el sistema como

g1(u,v)=f1(x,y)
g2(u,v)=f2(x,y)

nos preguntamos cuando del sistema podemos despejar a uy v en términos de x y y. Mas generalmente, consideramos el problema siguiente, dadas las funciones F y G de las variables u,v,x,y nos preguntamos cuando de las expresiones

F(x,y,u,v)=0
G(x,y,u,v)=0

podemos despejar a u y v en términos de x y y en caso de ser posible diremos que las funciones u=φ1(x,y) y v=φ2(x,y) son funciones implícitas dadas. Se espera que ∃′n funciones u=φ1(x,y) y v=φ2(x,y) en

F(x,y,φ1(x,y),φ2(x,y)
G(x,y,φ1(x,y),φ2(x,y)

con (x,y) en alguna vecindad V. Suponiendo que existen φ1 y φ2 veamos sus derivadas

∂F∂x∂x∂x+∂F∂y∂y∂x+∂F∂u∂u∂x+∂F∂v∂v∂x=0    ⇒    ∂F∂u∂u∂x+∂F∂v∂v∂x=−∂F∂x

∂G∂x∂x∂x+∂G∂y∂y∂x+∂G∂u∂u∂x+∂G∂v∂v∂x=0    ⇒    ∂G∂u∂u∂x+∂G∂v∂v∂x=−∂G∂x

Lo anterior se puede ver como un sistema de 2 ecuaciones con 2 incógnitas ∂u∂x y ∂v∂x. Aquí se ve que para que el sistema tenga solución

det|∂F∂u∂F∂v∂F∂u∂G∂v|≠0 en (P) (el det Jacobiano) y según la regla de Cramer.

∂u∂x=−det|−∂F∂x∂F∂v−∂G∂x∂G∂v|det|∂F∂u∂F∂v∂F∂u∂G∂v|,    ∂v∂x=−det|∂F∂u−∂F∂x∂G∂u−∂G∂x|det|∂F∂u∂F∂v∂F∂u∂G∂v|      (con los dos det Jacobianos).

Análogamente si derivamos con respecto a y obtenemos

∂F∂u∂u∂y+∂F∂v∂v∂y=−∂F∂y

∂G∂u∂u∂y+∂G∂v∂v∂y=−∂G∂y

de donde
∂u∂y=−det|−∂F∂y∂F∂v−∂G∂y∂G∂v|det|∂F∂u∂F∂v∂F∂u∂G∂v|,    ∂v∂y=−det|∂F∂u−∂F∂y∂G∂u−∂G∂y|det|∂F∂u∂F∂v∂F∂u∂G∂v|      (con los dos det Jacobianos).

Al determinante det|∂F∂u∂F∂v∂G∂u∂G∂v| lo llamamos Jacobiano y lo denotamos por ∂(F,G)∂(u,v).

Teorema de la Función Implícita (sistemas de ecuaciones)

Teorema 3. Considere las funciones z1=F(x,y,u,v) y z2=G(x,y,u,v). Sea P=(x,y,u,v)∈R4 un punto tal que F(P)=G(P)=0. Suponga que en una bola B∈R4 de centro P las funciones F y G tienen (sus cuatro) derivadas parciales continuas. Si el Jacobiano ∂(F,G)∂(u,v)(P)≠0 entonces las expresiones F(x,y,u,v)=0 y G(x,y,u,v)=0 definen funciones (implícitas) u=φ1(x,y) y v=φ2(x,y) definidas en una vecindad v de (x,y) las cuales tienen derivadas parciales continuas en v que se pueden calcular como se menciona arriba.

Demostración. Dado que det|∂F∂u∂F∂v∂F∂u∂G∂v|≠0 entonces ∂F∂u(p), ∂F∂v(p), ∂G∂u(p), ∂G∂v(p) no son cero al mismo tiempo, podemos suponer sin perdida de generalidad que ∂G∂v(p)≠0. Entonces la función z1=G(x,y,u,v) satisface las hipótesis del T.F.I y en una bola abierta con centro p, v se puede escribir como v=ψ(x,y,u).

Hacemos ahora
H(x,y,u)=F(x,y,u,ψ(x,y,u)) y tenemos que
∂H∂u=∂F∂x∂x∂u+∂F∂y∂y∂u+∂F∂u∂u∂u+∂F∂v∂ψ∂u=∂F∂u+∂F∂v∂ψ∂u

por otro lado
∂ψ∂u=−∂G∂u∂G∂v
por lo tanto
∂H∂u=∂F∂u+∂F∂v∂ψ∂u=∂F∂u+∂F∂v(−∂G∂u∂G∂v)=∂F∂u∂G∂v−∂F∂v∂G∂u∂G∂v≠0por lo tanto para H(x,y,u)=0 tenemos que existe una función u=φ1(x,y) y por lo tanto v=ψ(x,y,u)=ψ(x,y,φ1(x,y,u))=φ2(x,y) y por tanto u,v se pueden expresar en términos de x,y en una vecindad de p. ◻

El Teorema de la Función Implícita

Por Angélica Amellali Mercado Aguilar

Deja un comentario

Introduccion

El Teorema de la función implicita versión para funciones f:R→R

Teorema 1. Considere la función y=f(x). Sea (x0,y0)∈R2 un punto tal que F(x0,y0)=0. Suponga que la función F tiene derivadas parciales continuas en alguna bola con centro (x0,y0) y que ∂F∂y(x0,y0)≠0. Entonces F(x,y)=0 se puede resolver para y en términos de x y definir así una función y=f(x) con dominio en una vecindad de (x0,y0), tal que y0=f(x0), lo cual tiene derivadas continuas en V que pueden calcularse como y′=f′(x)=−∂F∂x(x,y)∂F∂y(x,y), x∈V.

Demostración. Como ∂F∂y(x0,y0)≠0 supongamos sin perdida de generalidad que ∂F∂y(x0,y0)>0. Por ser ∂F∂y continua en una vecindad de (x0,y0) entonces exite un cuadrado S, centrado en (x0,y0) totalmente contenido en esa vecindad, en donde ∂F∂y(x,y)>0 ∀ x,y∈S.Sea
S={(x,y)∈R2 | |x−x0|<h y |y−y0|<k}

En todo punto (x,y) que pertenece a S, ∂F∂y(x,y)>0. Esto quiere decir que en S, F es creciente y fijando x0 en [x0−h,x0+h] se tiene que F es creciente en [y0−k,y0+k] y se anula en y0, por lo que
F(x0,y0−k)<0  yF(x0,y0+k)>0 Consideremos ahora el par de funciones F(x,y0−k) y F(x,y0+k) definidas en el intervalo (x0−k,x0+k). Donde ambas funciones solo tienen x como variable. La primera función cumple F(x0,y0−k)<0 y por ser continua en x0, es negativa en toda una vecindad (x0−h1x0+h1) de x0. Análogamente, la segunda función cumple F(x0,y0+k)>0 y por ser continua en x0, es positiva en toda una vecindad (x0−h2x0+h2) de x0. Sea h=minh1,h2. Entonces para toda x tal que |x−x0| y F(x,y0+k)>0 Fijemos x en el intervalo (x0−h,x0+h), y consideremos a F(x,y), sólo como función de y, sobre [y0−k,y0+k]. Esta función cumple que

F(x,y0−k)<0 y F(x,y0+k)>0

por lo tanto según el teorema del valor intermedio, existe un único y en (y0−k,y0+k) tal que F(x,y)=0. Así queda establecida la existencia y unicidad de la función y=f(x). Donde además, y0=f(x0), y para todo x∈(x0−h,x0+h) F(x,f(x))=0,y  ∂F∂y(x0,y0)≠0

Vamos a comprobar que la función es continua, para ello se tiene
x∈[x0−h,x0+h] ⇒ |x−x0|<h
tomando h<δ se tiene
|x−x0|<δ
esto quiere decir que
|y−y0|<k es decir|f(x)−f(x0)|,∂F∂y(x0,y0)
existen y son continuas entonces F es diferenciable por lo que
F(x0+h,y0+k)−F(x0,y0)=∂F∂x(x0,y0)h+∂F∂y(x0,y0)k+R(h,k)
Tenemos que F es continua por lo que
F(x0+h,y0+k)−F(x0,y0)=0sih,k→0
también
R(h,k)→0sih,k→0
por lo que
∂F∂x(x0,y0)h+∂F∂y(x0,y0)k=0
esto es
kh=−∂F∂x(x0,y0)∂F∂y(x0,y0)
y cuando h,k→0 se tiene
dydx=−∂F∂x(x0,y0)∂F∂y(x0,y0)

Importante: Este es un resultado que garantiza la
existencia de una función y=f(x) definida implícitamente por
F(x,y)=0. Esto es, puede resolverse para y en términos de x,
pero no nos dice como hacer el despeje.

Ejemplo. Considere la función F(x,y)=e2y+x+sin⁡(x2+y)−1 en el punto (0,0) tenemos F(0,0)=0. Las derivadas parciales de F son
Fx=e2y+x+2xcos⁡(x2+y)
Fy=2e2y+x+cos⁡(x2+y)

que son siempre continuas. Además, ∂F∂y(0,0)=3≠0 de modo que T.F.Im. garantiza una vecindad de x=0 en la cual podemos definir una función y=f(x) tal que F(x,f(x))=0. Obsérvese que en este caso no podemos hacer explícita la función y=f(x) sin embargo tal función existe y su derivada es

y′=f′(x)=−∂F∂x∂F∂y=e2y+x+2xcos⁡(x2+y)2e2y+x+cos⁡(x2+y)

Ejemplo. Considere F(x,y)=x4−exy3−1 en el punto (1,1) F(1,1)=1−1=0, Fx=4x3−y3exy3−1 Por lo tanto, Fx|(1,1)=3, Fy=−3xyexy3−1
Y así, Fy|(1,1)=−3, y ∂F∂y=−3≠0.

El T.F.Im. nos garantiza que en los alrededores de (1,1) el nivel cero de F se ve como la gráfica de la función y=f(x) y que su derivada es y′=−4x3−y3exy3−1−3xy2exy3−1.

Observe que en este caso la función F permite hacer el despeje en términos de x.

F(x,y)=x4−exy3−1=0
x4=exy3−1
ln⁡(x4)=xy3−1
(ln⁡(x4)+1x)13=y=f(x) que al derivar se debe de llegar al mismo resultado.

Ejemplo. Considere F(x,y)=x2−y3−1 en el punto (x0,y0) con y0≠0 tal que F(x0,y0)=0, Fx=2x,  Fy=2y
Por lo tanto, Fx|(x0,y0)=2x0,
Y así, Fy|(x0,y0)=2y0, y ∂F∂y=2y0≠0.
El T.F.Im. nos garantiza que en los alrededores de (x0,y0) el
nivel cero de F se ve como la gráfica de la función y=f(x) y que su derivada es
y′(x)=−∂F∂x(x0,y0)∂F∂y(x0,y0)
en este caso
y′(x)=−2x02y0=−x0y0
si y0>0 tal función es f(x)=1−x2 por lo que
y′=−x1−x2=−xy
si y0<0 tal función es f(x)=−1−x2 por lo que
y′=−−x−1−x2=−xy

El Teorema de la función implicita versión para funciones f:R2→R

Considere la función F(x,y,z). Sea (x0,y0,z0)∈R3 un punto tal que F(x0,y0,z0)=0. Suponga que la función F tiene derivadas parciales ∂F∂x, ∂F∂y, ∂F∂z continuas en alguna bola con centro (x0,y0,z0) y que ∂F∂z(x0,y0,z0)≠0.
Entonces F(x,y,z)=0 se puede resolver para z en términos de x,y y definir así una función z=f(x,y) con dominio en una vecindad de
(x0,y0,z0), tal que z0=f(x0,y0), lo cual tiene derivadas continuas
en V que pueden calcularse como dzdx(x,y)=−∂F∂x(x,y)∂F∂z(x,y)   dzdy(x,y)=−∂F∂y(x,y)∂F∂z(x,y)
Importante: Este es un resultado que garantiza la existencia de una función z=f(x,y) definida implícitamente por F(x,y,z)=0. Esto es, puede resolverse para z en términos de x,y, pero no nos dice como hacer el despeje.

Demostración. Consideremos el par de funciones
F(x,y,z0−ℓ)yF(x,y,z0+ℓ)
definidas para (x,y)∈[x0−h,x0+h]×[y0−k,y0+k]\La primera satisface
F(x0,y0,z0−ℓ)<0 la segunda cumple F(x0,y0,z0+ℓ)>0
Fijemos (x,y) en [x0−h,x0+h]×[y0−k,y0+k] y consideramos F(x,y,z) solo como función de z, sobre [z0−ℓ,z0+ℓ]. Esta función cumple
F(x,y,z0−ℓ)<0 y F(x,y,z0+ℓ)>0
por lo que al aplicar el Teorema del valor intermedio, obteniendose un único z en (z0−ℓ,z0+ℓ) en donde F(x,y,z)=0.Queda así establecida la existencia y unicidad de la función z=f(x,y) con dominio [x0−h,x0+h]×[y0−k,y0+k] y rango [z0−ℓ,z0+ℓ] Vamos a probar que dicha f es continua, para ello si
(x∈[x0−h,y0+h],y∈[y0−k,y0+k]) ⇒ (|x−x0|<h‖y−y0|<k)
por lo que
|(x,y)−(x0,y0)|<|x−x0|+|y−y0|<h+k
si h<k
|(x,y)−(x0,y0)|<2k=δ
donde
|f(x,y)−f(x0,y0)|=|z−z0|<ℓ=ϵ
por lo tanto f(x,y) es continua.Ahora si suponemos que ∂F∂x, ∂F∂y, ∂F∂z son continuas en los alrededores de (x0,y0,z0) en tonces F es diferenciable y se tiene
F(x0+h,y0,z0+ℓ)−F(x0,y0,z0)=∂F∂x(x0,y0,z0)h+∂F∂y(x0,y0,z0)0+∂F∂z(x0,y0,z0)ℓ+R(h,k,ℓ)

De donde
F(x0+h,y0,z0+ℓ)−F(x0,y0,z0)→0
R(h,k,ℓ)→0
por lo que
∂F∂x(x0,y0,z0)h+∂F∂z(x0,y0,z0)ℓ=0
 ⇒ hℓ=−∂F∂x(x0,y0,z0)∂F∂z(x0,y0,z0)
y cuando h,ℓ→0 se tiene
dzdx=−∂F∂x(x0,y0,z0)∂F∂z(x0,y0,z0)
Análogamente
F(x0,y0+k,z0+ℓ)−F(x0,y0,z0)=∂F∂x(x0,y0,z0)0+∂F∂y(x0,y0,z0)k+∂F∂z(x0,y0,z0)ℓ+R(h,k,ℓ)
De donde
F(x0,y0+k,z0+ℓ)−F(x0,y0,z0)→0
R(h,k,ℓ)→0
por lo que
∂F∂y(x0,y0,z0)k+∂F∂z(x0,y0,z0)ℓ=0
 ⇒ kℓ=−∂F∂y(x0,y0,z0)∂F∂z(x0,y0,z0)
y cuando h,ℓ→0 se tiene
dzdy=−∂F∂y(x0,y0,z0)∂F∂z(x0,y0,z0) ◻

El Método de los Mínimos Cuadrados.

Por Angélica Amellali Mercado Aguilar

Deja un comentario

Introduccion

El método de los mínimos cuadrados

El método de mínimos cuadrados se aplica para ajustar rectas a una serie de datos presentados como punto en el plano.
Suponagamos que se tienen los siguientes datos para las variables x,y.

Esta situación se puede presentar en estudios experimentales, donde se estudia la variación de cierta magnitud x en función de otra magnitud y. Teóricamente es de esperarse que la relación entre estas variables sea lineal, del tipo
y=mx+b
El método de mínimos cuadrados nos proporciona un criterio con el cual podremos obtener la mejor recta que representa a los puntos dados. Se desearía tener
yi=mxi+b
para todos los puntos (xi,yi) de i=1,…,n. Sin embargo, como en general
yi≠mxi+b
se pide que la suma de los cuadrados de las diferencias (las desviaciones)
yi−(mxi+b)
sea la menor posible.

Se requiere
S=(y1−(mx1+b))2+(y2−(mx2+b))2+⋯+(yn−(mxn+b))2
=∑i=1n(yi−(mxi+b))2
sea lo más pequeña posible. Los valores de m y b que cumplan con esta propiedad, determinan la recta
y=mx+b
que mejor representa el comportamiento lineal de los puntos (xi,yi)

Consideremos entonces la función f de las variables m y b dada por
f(m,b)=∑i=1n(yi−(mxi+b))2
donde los puntos críticos de esta función se obtienen al resolver el sistema
∂f∂m=∑i=1n2(yi−(mxi+b))(−xi)=2∑i=1nxi(yi−(mxi+b))=0
∂f∂b=∑i=1n2(yi−(mxi+b))(−1)=−2∑i=1n(yi−(mxi+b))=0
De la segunda ecuación obtenemos
∑i=1nyi−m∑i=1nxi−∑i=1nb=0
de donde
b=1n∑i=1nyi−m(1n∑i=1nxi)
Llamemos
x―=1n∑i=1nxi
y―=1n∑i=1nyi
que son las medias aritméticas de los valores xi, yi respectivamente. Entonces
b=y―−mx―

sustituyendo en la ecuación
∂f∂m=0
nos queda
∑i=1nxi(yi−mxi−(y―−mx―))=0
de donde se obtiene
m=∑i=1nxi(yi−y―)∑i=1nxi(xi−x―)
En resumen, la función
f(m,b)=∑i=1n(yi−(mxi+b))2
tiene un único punto crítico para
m=∑i=1nxi(yi−y―)∑i=1nxi(xi−x―),   b=y―−mx―
Ahora vamos a verificar que en dicho punto crítico se alcanza un mínimo local, para lo cual recurrimos a nuestro criterio de la segunda derivada, en este caso
∂2f∂m2=−2∑i=1n−xi2=2∑i=1nxi2
∂2f∂m∂b=−∑i=1n−xi=2∑i=1nxi
∂2f∂b2=−2∑i=1n(−1)=2n

Tenemos que
∂2f∂m2>0
Por otro lado
(2∑i=1nxi)2−(2∑i=1nxi2)(2n)<0
esta desigualdad es equivalente a
(∑i=1nxi)2<n∑i=1nxi
La cual no es mas que la desigualdad de Cauchy-Schwarz aplicada a los vectores (1,1,…,1) y (x1,x2,…,xn) de Rn. Por lo que la función f posee un mínimo local en el punto punto crítico dado.

Ejemplo. Se obtuvieron experimentalmente los siguientes valores de las variables x, y, los cuales se sabe que guardan entre sí una relación lineal

Vamos a encontrar la recta que mejor se ajusta a estos datos, según el método de mínimos cuadrados se tiene
x―=1+2+3+42=2.5
y―=1.4+1.1+0.7+0.14=0.825
Aplicando la fórmula obtenida para m y b obtenemos
m=∑i=1nxi(yi−y―)∑i=1nxi(xi−x―)=1(1.4−0.825)+2(1.1−0.825)+3(0.7−0.825)+4(0.1−0.825)1(1−2.5)+2(2−2.5)+3(3−2.5)+4(4−2.5)
=−2.155=−0.43
b=y―−mx―=0.825−(0.43)(2.5)=1.9

por lo que la recta que mejor ajusta los datos proporcionados

La suma de las diferencias de la recta y real con la y predicha por la ecuación obtenida es
−0.07+0.06+0.09−0.08=0
Es decir nuestra recta efectivamente compensa los puntos que quedaron por encima con puntos que quedaron por debajo. Gráficamente esto se ve.

La mejor recta que ajusta los datos del ejemplo.

Mas adelante

Tarea Moral

Enlaces

Multiplicadores de Lagrange

Por Angélica Amellali Mercado Aguilar

Deja un comentario

Introducción

Para entender el método de los multiplicadores de Lagrange ilustraremos las ideas con un ejemplo.

Ejemplo. Sea f:R2→R dada por
f(x,y)=(x+1)2+y2
En este caso vamos a encontrar los puntos críticos

∇f(x,y)=(2(x+1),2y) ⇒ ∇f(x,y)=(0,0) ⇔ 2(x+1)=02y=0 ⇔ x=−1y=0
por lo tanto el único punto crítico es (−1,0) para ver si es máximo o mínimo nos fijamos que en la función
f(x,y)=(x+1)2+y2 ⇒ f(x,y)≥0
en este caso cuando evaluamos en el punto crítico (−1,0) se tiene
f(−1,0)=(−1+1)2+02=0

por lo que podemos decir que el punto (−1,0) es un punto mínimo.

La pregunta ahora es si la función alcanza un valor máximo, para ello debemos restringir el dominio de la función, en este caso al conjunto
{(x,y)∈R2 | |(x,y)|≤2}

en la parte roja se calculo que f alcanzaba un valor mínimo en (−1,0) falta ver lo que ocurre en la frontera del conjunto, es decir en la parte azul. Esta parte se puede parametrizar.

donde α:[0,2π]→R2
Podemos entonces definir la función g(t)=f∘α (t) en este caso
g(t)=f∘α(t)=f(α(t))
=f(2cos⁡ t,2sen t)
=(2cos⁡ t+1)2+4sen2 t
=4cos⁡ t+5
lo que haremos ahora es encontrar los valores máximos y mínimos sobre g, en este caso

g′(t)=−4sent
por lo que
g′(t)=0 ⇔ −4sent=0 ⇔ t=0, t=π, t=2π
evaluando en g se tiene

g(0)=4cos2⁡(0)+5
=9
g(π)=4cos⁡π+5
=1
g(2π)=4cos2⁡(2π)+5
=9
se tiene entonces que el máximo valor se alcanza en t=0, t=2π y el mínimo valor se alcanza en t=π
Ahora sobre la frontera se tiene

α(0)=(2cos⁡ 0,2sen 0)=(2,0)
α(π)=(2cos⁡π,senπ)=(−2,0)
α(2π)=(2cos⁡ 2π,sen 2π)=(2,0)
por lo tanto tenenmos que el valor mínimo de f sobre el conjunto es 1 y que este valor se alcanza en (−2,0)

y su valor máximo sobre el conjunto es 9 y que este valor se alcanza en (−2,0).\Por lo tanto comparando los valores de f en los puntos críticos que estan en el interior del conjunto
{(x,y)∈R2 | ||(x,y)||=2}
junto con los valores en la frontera de dicho conjunto, concluimos que f alcanza sus valores máximo y mínimo en los puntos (−1,0) y (2,0)

El conjunto
{(x,y)∈R2 | ||(x,y)||≤2}
se puede considerarse como el conjunto de nivel de una función g:R2→R en el caso de nuestro ejemplo la función g es
g(x,y)=x2+y2
Vamos a considerar los conjuntos de nivel de la función
f(x,y)=(x+1)2+y2
para c=1 y c=9 (que son los valores extremos que alcanzo f sobre el nivel 4 de g)

Observamos que estos conjuntos de nivel N1(f) y N9(f) se intersectan tangencialmente con N4(g) en los puntos (−2,0) y (2,0) que son justo los puntos en donde f alcanza sus valores extremos sobre la frontera del conjunto.Recordando que el gradiente de una función en un punto x0 es ortogonal al conjunto de nivel que contiene a este punto, concluimos que los vectores
∇f(−2,0),∇g(−2,0)

deben de ser paralelos y lo mismo para

∇f(2,0), ∇g(2,0)
vamos averificar
(∇f(−2,0)=(−2,0)∇g(−2,0)=(−4,0)) ⇒ ∇f(−2,0)=12∇g(−2,0)
(∇f(2,0)=(6,0)∇g(2,0)=(4,0)) ⇒ ∇f(2,0)=32∇g(2,0)

Conjeturamos lo siguiente:
Si tenemos una función f para la cual queremos calcular sus valores extremos sobre un conjunto de nivel de una función g y localizar los puntos de este conjunto en los cuales alcanza estos valores extremos, es suficiente con encontrar los puntos x^∈Nc(g) en los cuales se satisface que

∇f(x^)=λ∇g(x^)

Teorema 1. Método de los multiplicadores de lagrange.

Sean f:u⊂Rn→R y g:u⊂Rn→R funciones C1 con valores reales dados. Sean x0∈u y g(x0)=c, y sea S el conjunto de nivel de g con valor c. Suponer ∇g(x0)≠0. Si f|s (f restringida a s) tiene un máximo o un mínimo local en S, en x0, entonces existe un número real λ tal que ∇f(x0)=λ∇g(x0).

Demostración. Para n=3 el espacio tangente o plano tangente de S en x0 es el
espacio ortogonal a ∇g(x0) y para n arbitraria podemos dar la misma definición de espacio tangente de S en x0. Esta definición se puede motivar al considerar tangentes a trayectorias c(t) que estan en s, como sigue: si c(t) es una trayectoria en S y c(0)=x0, entonces c′(0) es un vector tangente a S en x0, pero
dg(c(t))dt=ddt(c)=0
Por otro lado usando regla de la cadena
ddtg(c(t))|t=0=∇g(x0)⋅c′(0)

de manera que ∇g(x0)⋅c′(0)=0, esto es, c′(0) es ortogonal a ∇g(x0). Si f|s tiene un máximo en x0, entonces f(c(t)) tiene un máximo en t=0. Por cálculo de una variable, df(c(t))dt|t=0=0. Entonces por regla de la cadena

0=df(c(t))dt|t=0=∇f(x0)⋅c′(0)
Asi, ∇f(x0) es perpendicular a la tangente de toda curva en S y entonces tambien es perpendicular al espacio tangente completo de S en x0. Como el espacio perpendicular a este espacio tangente es una recta, ∇f(x0) y ∇g(x0) son paralelos. Como ∇g(x0)≠0, se deduce que ∇f(x0) es multiplo de ∇g(x0). ◻

Ejemplo. Use el método de los multiplicadores de Lagrange para encontrar los valores extremos de la función f:R2→R dada por
f(x,y)=2x+3y sobre la restricción
x2+y2=4

Solución. En este caso la restricción la vemos como el conjunto de nivel cero de la función
g(x,y)=x2+y2−4
y tenemos entonces que
(∇f=(2,3)∇g=(2x,2y)) ⇒ (2,3)=λ(2x,2y)
tenemos el sistema

(2=2λx3=λ2y) ⇒ (λ=1xλ=32y) ⇒ 1x=32y ⇒ y=32x
dicho valor se sustituye en la restricción

x2+(32x)2=4 ⇒ x2+94x2=4 ⇒ 134x2=4 ⇒ 13x2=16 ⇒ x2=1613 ⇒ |x|=413
por lo que
(y=32(413)=613y=−32(413)=−613)
evaluando en nuestra función

El método de Lagrange se puede utilizar cuando hay más de una ecuación de restricción, pero se debe añadir otro multiplicador por cada restricción adicional. Si se requiere hallar los valores extremos de f(x,y,z) sujetos a las restricciones g(x,y,z)=0 y h(x,y,z)=0 entonces la condición de Lagrange es
∇f=λ∇g+μ∇h
sujeto a
g(x,y,z)=0
h(x,y,z)=0

Ejemplo. La intersección del plano
x+12y+13z=0
con la esfera
x2+y2+z2=1 es un circulo. Halle el punto sobre este círculo con coordenada x máxima
Solución Se requiere maximizar la función
f(x,y,z)=x
sujeta a
x+12y+13z=0,   x2+y2+z2=1
tenemos entonces
(∇f=(1,0,0)∇g=(1,12,13)∇h=(2x,2y,2z)) ⇒ (1,0,0)=λ(1,12,13)+μ(2x,2y,2z)

es decir
λ+μ2x=112λ+μ2y=013λ+μ2z=0 ⇒ μ=1−λ2xλ=−4μyλ=−6μz
las dos últimas nos llevan a
−4μy=−6μz ⇒ y=32z
este valor se sustituye en la primer restricción (plano)
x+12(32z)+13z=0 ⇒ x=−1312z
ambos valores se sustituyen en la segunda restricción (esfera)

(−1312z)2+(32z)2+z2=1 ⇒ z=±12713
por lo que los valores de x,y son
x=±137
y=±18713
Tenemos entonces los puntos
P=(−137,18713,12713),  Q=(137,−18713,−12713)
donde Q es el punto con mayor coordenada x.

Continuación extremos locales.

Por Angélica Amellali Mercado Aguilar

Deja un comentario

Introducción

Extremos Locales parte 2

Entre las caracteristicas geometricas básicas de la gráficas de una
función estan sus puntos extremos, en los cuales la función alcanza
sus valores mayor y menor.

Definición 1. Si f:u⊂Rn→R es una función escalar, dado un punto x0∈u
se llama mínimo local de f si existe una vecindad v de x0 tal que ∀x∈v , f(x)>f(x0). De manera analoga, x0∈u es un máximo local si existe una vecindad v de x0 tal que f(x)<f(x0), ∀x∈v. El punto x0∈u es un extremo local o relativo, si es un mínimo local o máximo local.

Teorema 1. Criterio de la primera derivada Si u∈R es abierto, la función f:u⊂Rn→R es diferenciable y x0∈u es un extremo local entonces ∇f(x0)=0, esto es x0 es un punto crítico de f.

Demostración. Supongamos que t alcanza su máximo local en x0. Entonces para cualquier h∈Rn la función g(t)=f(x0+th) tiene un máximo local en t=0. Asi, del cálculo de una variable g′(0)=0 ya que como g(0) es máximo local, g(t)≤g(0) para t>0 pequeño

∴g′(0)=limt→t0+g(t)−g(0)t=0

Análogamente para t<0 pequeño tomamos

g′(0)=limt→t0−g(t)−g(0)t=0

Ahora por regla de la cadena g′(0)=∂f∂x1(x0)h1+∂f∂x2(x0)h2+⋯+∂f∂xn(x0)h0=∇f(x0)⋅h
Así ∇f(x0)⋅h=0∀h de modo que ∇f(x0)=0. En resumen si x0 es un extremo local, entonces ∂f∂xi(x0)=0∀ i=1,…,n. En otras palabras ∇f(x0)=0.

Ejemplo. Hallar los máximos y mínimos de la función f:R2→R, definida por f(x,y)=x2+y2−2x−6y+14

Solución. Debemos identificar los puntos críticos de f resolviendo ∂f∂x=0, ∂f∂y=0 para x,y, 2x−2=0   2y−6=0 De modo que el punto crítico es (1,3). Como f(x,y)=(x2−2x+1)+(y2−6y+9)+4=(x−1)2+(y−3)2+4
tenemos que f(x,y)≥4 por lo tanto en (1,3) f alcanza un mínimo relativo.

Ejemplo. Considerar la función f:R2→R,
f(x,y)=4−x2−y2 entonces ∂f∂x=−2x, ∂f∂y=−2y. f solo tiene un punto crítico en el origen, donde el valor de f es 4. Como f(x,y)=4−(x2+y2)
tenemos que f(x,y)≤4 por lo tanto en (0,0) f alcanza un máximo relativo.

Ejemplo. En el siguiente ejemplo mostramos que no todo punto critico es un valor extremo\Sea f(x,y)=x2y+y2x tenemos que sus puntos criticos son
∂f∂x=2xy+y2   ∂f∂y=2xy+x2=0
por lo tanto

(2xy+y2=02xy+x2=0)⇔(x=yx=−y)

tomando x=−y tenemos que
2xy+y2=0 ⇒ −2y2+y2=0 ⇒ −y2=0⇒ y=0 ⇒ x=0
tomando x=y tenemos que
2xy+y2=0 ⇒ 2y2+y2=0 ⇒ −3y2=0⇒ y=0 ⇒ x=0
por lo tanto (0,0) es el único punto critico.

Ahora bien para f(x,y) tomamos x=y
f(x,x)=2x3
la cual es (<0 si x<0) y (>0 si x>0) por lo tanto el punto critico (0,0) no es ni máximo ni mínimo local de f

Ahora bien para f(x,y) tomamos x=−y
f(x,−x)=0   ∀x
por lo tanto el punto critico (0,0) no es ni máximo ni mínimo local de f

Para el caso de funciones f:R3→R tenemos que recordando un poco de la expresión de taylor
f(x,y)=f(x0,y0)+(∂f∂x)p(x−x0)+(∂f∂y)p(y−y0)+(∂f∂z)p(z−z0)+

12!(∂2f∂x2p(x−x0)2+2∂2f∂x∂yp(x−x0)(y−y0)+∂2f∂y2p(y−y0)2+2∂2f∂x∂zp(z−z0)(x−x0)+2∂2f∂y∂zp(z−z0)(y−y0))
+∂2f∂z2p(z−z0)

Haciendo x−x0=h1,y−y0=h2,z−z0=h3 podemos escribir el término rojo de la siguiente manera

12!(∂2f∂x2h12+2∂2f∂x∂yh1h2+∂2f∂y2h22+2∂2f∂x∂zh3h1+2∂2f∂y∂zh3h2+∂2f∂z2h32)

y también se puede ver como producto de matrices
12!(h1 h2 h3)(∂2f∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z2)p(h1h2h3)

Si (x0,y0,z0) es un punto critico de la función entonces en la expresión de Taylor
f(x,y)=f(x0,y0)+(∂f∂x)p(x−x0)+(∂f∂y)p(y−y0)+(∂f∂z)p(z−z0)

12!(∂2f∂x2p(x−x0)2+2∂2f∂x∂yp(x−x0)(y−y0)+∂2f∂y2p(y−y0)2+2∂2f∂x∂zp(z−z0)(x−x0)+2∂2f∂y∂zp(z−z0)(y−y0))

+∂2f∂z2p(z−z0)(x−x0)

El término
∂f∂xp(x−x0)+∂f∂yp(y−y0)+∂f∂zp(z−z0)=0
y por lo tanto
f(x,y)−f(x0,y0)=12!(h1 h2 h3)(∂2f∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z2)p(h1h2h3)

vamos a determinar el signo de la forma
Q(h)=12!(h1 h2 h3)(∂2f∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z2)p(h1h2h3)

vamos a trabajar sin el término 12! que no afectara al signo de la expresión, tenemos entonces

Q(h)=(h1 h2 h3)(∂2f∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z2)p(h1h2h3)=∂2f∂x2h12+2∂2f∂x∂yh1h2+∂2f∂y2h22+2∂2f∂x∂zh3h1+2∂2f∂y∂zh3h2+∂2f∂z2h32
=∂2f∂x2(h1+∂2f∂y∂x∂2f∂x2h2)2+(∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2∂2f∂x2)h22+2∂2f∂x∂zh3h1+2∂2f∂y∂zh3h2+∂2f∂z2h32

hacemos b1=∂2f∂x2,h1′=(h1+∂2f∂y∂x∂2f∂x2h2),b2=∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2∂2f∂x2,  h2′=h2 y obtenemos

=b1h1′2+b2h2′2+2∂2f∂x∂zh3h1+2∂2f∂y∂zh3h2+∂2f∂z2h32

que podemos escribir
=b1h1′2+b2h2′2+2∂2f∂x∂z(h1+∂2f∂y∂x∂2f∂x2h2−∂2f∂y∂x∂2f∂x2h2)h3+2∂2f∂y∂zh3h2+∂2f∂z2h32

=b1h1′2+b2h2′2+2∂2f∂x∂z(h1′−∂2f∂y∂x∂2f∂x2h2′)h3+2∂2f∂y∂zh3h2+∂2f∂z2h32

=b1h1′2+b2h2′2+2∂2f∂x∂zh1′h3+(2∂2f∂y∂z−2∂2f∂x∂z∂2f∂y∂x∂2f∂x2)h2′h3+∂2f∂z2h32

hacemos
2b23=2∂2f∂y∂z−2∂2f∂x∂z∂2f∂y∂x∂2f∂x2y obtenemos
=b1h1′2+b2h2′2+2∂2f∂x∂zh1′h3+2b23h2′h3+∂2f∂z2h32
que se puede escribir

=b1(h1′2+2∂2f∂x∂zb1h1′h3+(∂2f∂x∂zh3b1)2)+b2(h2′2+2b23b2h2′h3+(b23b2h3)2)+(∂2f∂z2−(∂2f∂x∂z)2b1−b232b2)h32

hacemos
b3=∂2f∂z2−(∂2f∂x∂z)2b1−b232b2
y obtenemos

=b1(h1′2+2∂2f∂x∂zb1h1′h3+(∂2f∂x∂zh3b1)2)+b2(h2′2+2b23b2h2′h3+(b23b2h3)2)+b3h32
=b1(h1′+∂2f∂x∂zb1h3)2+b2(h2′+b23b2h3)2+b3h32
esta última expresión será positiva si y solo si b1>0  b2>0 y b3>0 en clases pasadas vimos los dos primeros, veamos ahora que b3=∂2f∂z2−(∂2f∂x∂z)2b1−b232b2>0
tenemos entonces que

∂2f∂z2−(∂2f∂x∂z)2b1−b232b2=∂2f∂z2−(∂2f∂x∂z)2∂2f∂z2−(∂2f∂y∂z−2∂2f∂x∂z∂2f∂y∂x∂2f∂x2)2∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2∂2f∂x2

=∂2f∂z2∂2f∂x2(∂2f∂x∂z)2∂2f∂x2−(∂2f∂y∂z∂2f∂x2−∂2f∂x∂z∂2f∂y∂x)2(∂2f∂x2)2∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2∂2f∂x2=∂2f∂z2∂2f∂x2(∂2f∂x∂z)2∂2f∂x2−(∂2f∂y∂z∂2f∂x2−∂2f∂x∂z∂2f∂y∂x)2(∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2)∂2f∂x2

=(∂2f∂z2∂2f∂x2−(∂2f∂x∂z)2)(∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2)−(∂2f∂y∂z∂2f∂x2−∂2f∂x∂z∂2f∂y∂x)2∂2f∂x2(∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2)

=∂2f∂z2∂2f∂x2∂2f∂y2∂2f∂x2−∂2f∂z2∂2f∂x2(∂2f∂y∂x)2−∂2f∂y2∂2f∂x2(∂2f∂x∂z)2+(∂2f∂x∂z)2(∂2f∂y∂x)2−(∂2f∂y∂z)2(∂2f∂x2)2−∂2f∂x2(∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2)

2(∂2f∂x2∂2f∂y∂z∂2f∂x∂z∂2f∂y∂x)−(∂2f∂x∂z)2(∂2f∂y∂x)2∂2f∂x2(∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2)
=∂2f∂z2∂2f∂y2∂2f∂x2−∂2f∂z2(∂2f∂y∂x)2−∂2f∂y2(∂2f∂x∂z)2−(∂2f∂y∂z)2∂2f∂x2+2∂2f∂y∂z∂2f∂x∂z∂2f∂y∂x∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2

=|∂2f∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z2|∂2f∂y2∂2f∂x2−(∂2f∂y∂x)2

por lo tanto
b3>0 ⇔ |∂2f∂x2∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y2∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z2|>0

Un poco de Algebra Lineal

Si A∈Mn×n una matriz simétrica entonces existe una B∈Mn×n una matriz ortonormal tal que
BABT
es una matriz diagonal, es decir

BABT=[λ1⋯00⋱⋮0⋯λn]
Las matrices ortonormales se usan para realizar un cambio de base.

Si F:Rn→R es una forma cuadrática que tiene asociada la matriz simétrica A (en una base ortonormal) es decir
F(x1,x2,…,xn)=(x1⋯xn)A(x1⋯xn)T
existe entonces una base ortonormal tal que la matriz asociada a F en esta nueva base es una matriz diagonal.

Tenemos que si
B=[b11⋯b1n⋮⋱⋮bn1⋯bnn]
es tal que BABT es diagonal entonces
(x1⋯xn)=[x1′⋯xn′][b11⋯b1n⋮⋱⋮bn1⋯bnn]
=[x1′⋯xn′]B
Por lo que
F(x1,x2,…,xn)=(x1⋯xn)A(x1⋯xn)T
=F(x1,x2,…,xn)=(x1′⋯xn′)BA(x1′⋯xn′B)T
=(x1′⋯xn′)BABT(x1′⋯xn)T
=(x1′⋯xn′)[λ1⋯00⋱⋮0⋯λn](x1′⋯xn)T
=λ1x12+λ2x22+⋯+λnxn2

por lo que F es positiva si λ1,⋯,λn son positivos, de igual manera F es negativa si λ1,⋯,λn son negativos

Si definimos, para cada k∈1,…,n
Dk=[λ1⋯0⋮⋱⋮0⋯λk]

entonces
det(Dk)=λ1⋅λ2⋯λk
de tal forma que podemos decir que F es positiva si det(Dk)>0 y también F es negativa si det(Dk)<0 lo cual ocurre si det(Dk)<0 si k es impar y det(Dk)>0 si k es par para cada k∈{1,..,n}

Definición 2. La forma Q(x)=xAxt, que tiene asociada la matriz A (respecto a la base canónica de Rn) se dice:
Definida positiva, si Q(x)>0 ∀x∈ Rn

La forma Q(x)=xAxt, que tiene asociada la matriz A (respecto a la base canónica de Rn) se dice:
Definida negativa, si Q(x)<0 ∀x∈ Rn

Definición 3. Si la forma Q(x)=xAxt es definida positiva, entonces f tiene un mínimo local en en x. Si la forma Q(x)=xAxt es definida negativa, entonces f tiene un máximo local en en x.

Definición 4. Dada una matriz cuadrada A=aijj=1,…,ni=1,…,n se consideran las submatrices angulares Akk=1,…,n definidas como A1=(a11) A2=(a11a12a21a22)  A3=(a11a12a13a21a22a23a31a32a33),⋯,An=A
se define detAk=△k

Criterio 1 (a) Se tiene entonces que la forma Q(x)=xAXt es definida positiva si y solo si todos los determinantes △k  k=1,…,n son números positivos.

Criterio 1 (b) La forma Q(x)=xAXt es definida negativa si y solo si los dterminantes △kk=1,…,n tienen signos alternados comenzando por $\triangle_{1}<0,\triangle_{2}>0,…$ respectivamente.

Ejemplo. Consideremos la función f:R3→R f(x,y,z)=sin⁡x+sin⁡y+sin⁡z−sin⁡(x+y+z), el punto P=(π2,π2,π2) es
un punto crítico de f y en ese punto la matriz hessiana de
f es H(p)=[−2−1−1−1−2−1−1−1−2]

los determinantes de las submatrices angulares son
Δ1=det(−2) Δ2=det[−2−1 −1−2 ]

Δ3=detH(p)=−4 puesto que son signos alternantes con Δt<0 concluimos que la funcion f tiene en (π2,π2,π2) un máximo local. Este máximo local vale f(π2,π2,π2)=4