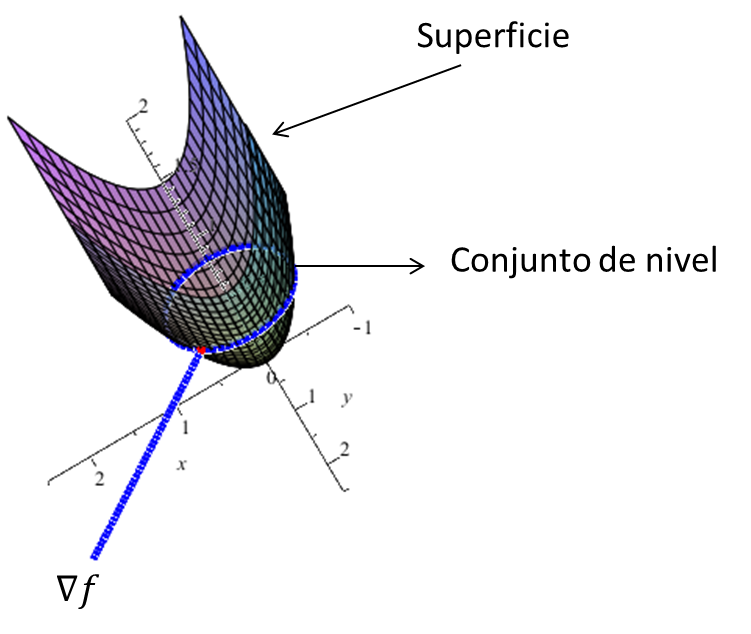
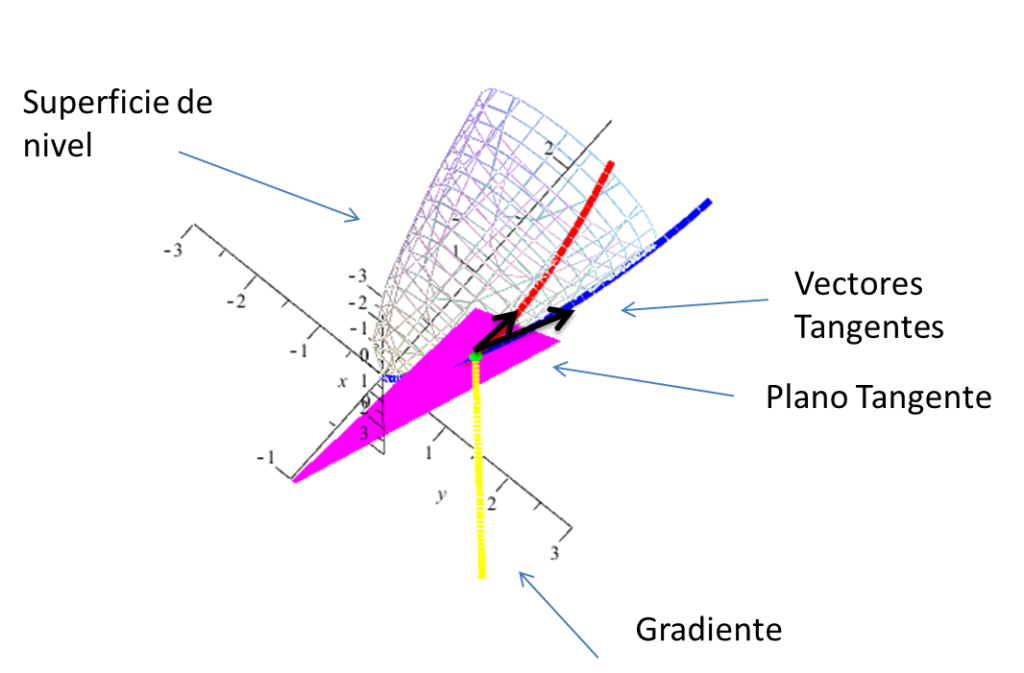
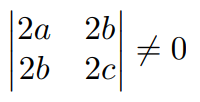$\textcolor{Red}{\textbf{Aproximación de Taylor para funciones $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$}}$

El caso de la aproximación con $n=2$ nos queda
$$f(x,y)=f(x_{0},y_{0})+\textcolor{Blue}{\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)}+$$

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})(x-x_{0})^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})(x-x_{0})(y-y_{0})+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})(y-y_{0})^{2}\right)}+R_{2}$$
Donde la expresión azul se puede escribir

$$\textcolor{Blue}{\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)=\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})}$$
y la expresión en rojo

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x{0})^{2}+2\frac{\partial^{2}f}{\partial y \partial
x}{p}(x-x{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y{0})^{2}\right)}$$ Define una forma cuadratica que
podemos escribir

$$\textcolor{Red}{\frac{1}{2!}(x-x_{0}\quad y-y_{0})\left(\begin{array}{cc}
\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y \partial x}\\
\frac{\partial^{2}f}{\partial x \partial y }&\frac{\partial^{2}f}{\partial y^{2}} \end{array}\right)\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)}$$

Por lo que el desarrollo de Taylor se puede escribir
$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})\left(\begin{array}{cc}
\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y \partial x} \\
\frac{\partial^{2}f}{\partial x \partial y }&\frac{\partial^{2}f}{\partial y^{2}} \end{array}\right)\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

A la matriz

$$\left(\begin{array}{cc}
\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y \partial x} \\
\frac{\partial^{2}f}{\partial x \partial y }&\frac{\partial^{2}f}{\partial y^{2}} \end{array}\right)$$

se le conoce como matriz Hessiana y se denota $H(x_{0},y_{0})$ por lo que el desarrollo de Taylor se puede escribir
$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

$\textcolor{Red}{\textbf{Aproximación de Taylor para funciones $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$}}$

Sea $f:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}$ y sea $F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)$ con $t\in[0,1]$, de esta manera f recorre el segmento de $[x_{0},y_{0},z_{0}]$ a $[x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t]$. Se tiene entonces que usando la regla de la cadena

$$F'(t)=\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)\cdot \frac{d(x_{0}+h_{1}t)}{dt}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)\cdot \frac{d(y_{0}+h_{2}t)}{dt}+$$

$$\frac{\partial f}{\partial z}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)\cdot \frac{d(z_{0}+h_{3}t)}{dt}=$$

$$\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3})\cdot h_{1}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3})\cdot h_{2}+\frac{\partial f}{\partial z}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3})\cdot h_{3}$$

Vamos ahora a calcular $F^{´´}(t)$

$$F^{´´}(t)=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}+\frac{\partial f}{\partial z}h_{3}\right)h_{1}+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}+\frac{\partial f}{\partial z}h_{3}\right)h_{2}+\frac{\partial}{\partial z}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}+\frac{\partial f}{\partial z}h_{3}\right)h_{3}=$$

$$\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
Ahora bien si se aplica la fórmula de Taylor con la forma del residuo de Lagrange a la función $$F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t)$$ y ponemos $t=0$, y $n=2$ se tiene

$$F(t)=F(0)+\frac{1}{1!}F'(0)t+\frac{1}{2!}F^{´´}(0)t^{2}+R_{2}$$

ahora bien con $t=1$, $x=x_{0}+h_{1}$, $y=y_{0}+h_{2}$, $z=z_{0}+h_{3}$

$$f(x,y)=f(x_{0},y_{0})+\textcolor{Blue}{\left(\frac{\partial f}{\partial
x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})}+$$

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x_{0})^{2}+2\frac{\partial^{2}f}{\partial x \partial
y}{p}(x-x_{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y_{0})^{2}+2\frac{\partial^{2}f}{\partial
x\partial z}{p}(z-z_{0})(x-x_{0})+2\frac{\partial^{2}f}{\partial
y\partial z}{p}(z-z_{0})(y-y_{0})\right)}$$

$$\textcolor{Red}{+\frac{\partial^{2}f}{\partial
z^{2}}{p}(z-z_{0})}+R_{2}$$
Donde la expresión en azul se puede escribir

$$\textcolor{Blue}{\left(\frac{\partial f}{\partial
x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})=\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})}$$

y la expresión en rojo
$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}\right)}$$

se puede ver como producto de matrices

$$\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial y \partial x}&\frac{\partial^{2}f}{\partial z \partial x}\\ \frac{\partial^{2}f}{\partial x \partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial z \partial y}\\ \frac{\partial^{2}f}{\partial
x \partial z}&\frac{\partial^{2}f}{\partial y \partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

La matriz
$$\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x \partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z \partial y}\\\frac{\partial^{2}f}{\partial
x \partial z}&\frac{\partial^{2}f}{\partial
y \partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)$$
se le conoce como matriz Hessiana y se le denota $H(x_{0},y_{0},z_{0})$, por lo que la aproximación de Taylor se puede escribir

$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(h_{1}~h_{2}~h_{3})H(x_{0},y_{0},z_{0})\left(\begin{matrix}h_{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

$\textbf{Ejemplo}$ Considere la función $f(x,y)=e^{2x+3y}$
$f[(0,0)+(x,y)]=f(0,0) +\nabla f(0,0)\cdot(x,y)+\frac{1}{2}[xy]H(0,0)\left[\begin{array}{c} x\\y\end{array}\right]+r_2(x,y)$

donde $\displaystyle\lim _{(x,y)\rightarrow(0,0)} \displaystyle\frac{r(x,y)}{x^2+y^2}=0$

$\nabla f=\left(\displaystyle\frac{\partial f}{\partial x}, \displaystyle\frac{\partial f}{\partial y}\right)=(2e^{2x+3y},3e^{2x+3y})~~~~ \therefore \nabla f(0,0)=(2,3)$

$$
H(x,y)=\left[\begin{array}{cc}
\displaystyle\frac{\partial ^2f}{\partial x^2} & \displaystyle\frac{\partial ^2f}{\partial y\partial x}\\
\displaystyle\frac{\partial ^2f}{\partial x\partial y} & \displaystyle\frac{\partial ^2f}{\partial y^2}\end{array}\right]=
\left[\begin{array}{cc}
4e^{2x+3} & 6e^{2x+3y}\\
6e^{2x+3y} & 9e^{2x+3y}\end{array}\right] ~~~~ \therefore H(0,0)= \left(\begin{array}{cc} 4&6\\6&9\end{array}\right)
$$

Así

Así $f(x,y)=f(0,0)+(2,3)\cdot (x,y) +\frac{1}{2}[xy]\left(\begin{array}{cc} 4&6\\6&9 \end{array}\right)\left[\begin{array}{c} x\\y\end{array}\right]+r(x,y)$
$\therefore e^{2x+3y}=1+2x+3y+2x^2+6xy\frac{9}{2}y^2+r(x,y)$

$\textcolor{Red}{\textbf{Extremos Locales}}$

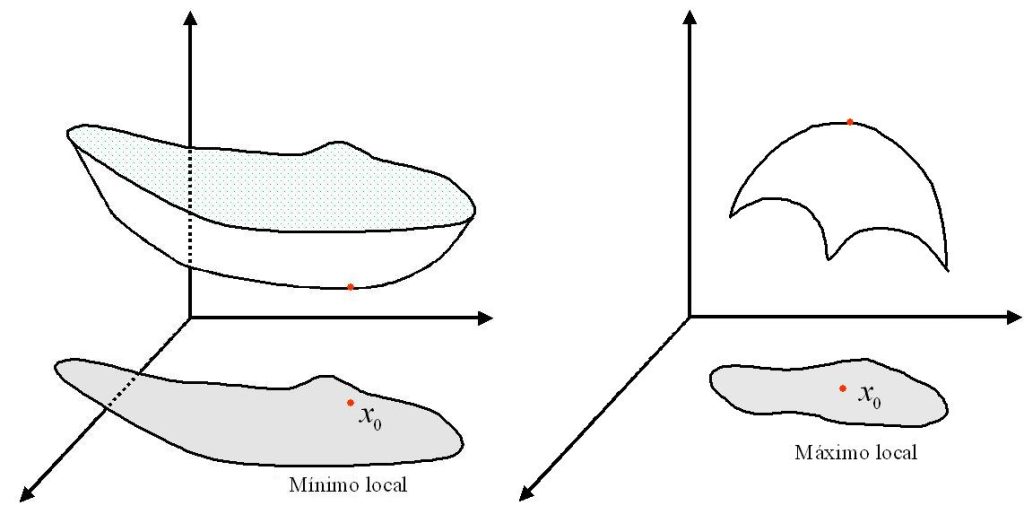
Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor.

$\textbf{Definición 1.}$ Si $f:u\subset \mathbb{R}^n \rightarrow
\mathbb{R}$ es una función escalar, dado un punto $x_0 \in u$
se llama mínimo local de $f$ si existe una vecindad $v$ de $x_0$ tal que $\forall x \in v$ ,$f(x)>f(x_0)$. De manera analoga, $x_0 \in u$ es un máximo local si existe una vecindad $v$ de $x_0$ tal que $f(x)<f(x_0)$, $\forall \quad x \in v$. El punto $x_0 \in u$ es un extremo local o relativo, si es un mínimo local o máximo
local.

En la expresión del desarrollo de Taylor
$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$
Si consideramos los valores para los cuales

$$\nabla f(x_{0},y_{0},z_{0})=(0,0,0)$$
es decir los puntos críticos del gradiente entonces nuestra aproximación de Taylor nos queda

$$f(x,y)=f(x_{0},y_{0})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$
que se puede escribir
$$f(x,y)-f(x_{0},y_{0})=\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

por lo que el signo del lado izquierdo $f(x,y)-f(x_{0},y_{0})$ dependerá del signo de la expresión
$$\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

es decir dependerá del signo de la forma
$$\frac{1}{2!}(h_{1}~h_{2})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

$\textbf{Teorema 1.}$ Sea $B=\left[\begin{array}{cc}
a & b \\
b & c \\
\end{array}
\right]$ y $H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a & b \\
b & c \\
\end{array}
\right]\left(
\begin{array}{c}
h_1 \\
h_2
\end{array}
\right)$ entonces $H(h)$ es definida positiva si y solo si $a>0$ y $ac-b^2>0$

$\small{Demostración.}$ Tenemos $$H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a h_1& bh_2 \\
b h_1& ch_2 \
\end{array}
\right]=\frac{1}{2}(ah_1^2+2bh_1h_2+ch_1^2)$$
si completamos el cuadrado
$$H(h)=\frac{1}{2}a\left(h_1+\frac{b}{a}h_2\right)^2+\frac{1}{2}\left(c-\frac{b^2}{a}\right)h_2^2$$
supongamos que $h$ es definida positiva. Haciendo
$h_2=0$ vemos que $a>0$. Haciendo $h_1=-\frac{b}{a}h_2$ $c-\frac{b^2}{a}>0$ ó $ac-b^2>0$. De manera analoga $H(h)$ es definida negativa si y solo si $a<0$ y $ac-b^2>0$. $\square$

Criterio del máximo y del mínimo para funciones de dos variables Sea $f(x,y)$ de clase
$C^3$ en un conjunto abierto $u$ de $\mathbb{R}^2$. Un punto $x_0,y_0$ es un mínimo local (Estricto) de $f$ si se cumple las siguientes tres condiciones:

$I)$ $\frac{\partial f}{\partial x}(x_0,y_0)=\frac{\partial f}{\partial y}(x_0,y_0)$
$II)$$\frac{\partial^2 f}{\partial x^2}(x_0,y_0)> 0$
$III)$ $\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right)-\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2> 0$ en $(x_0,y_0)$ (Discriminante). Si en II) tenemos $<0$ en lugar de $>0$ sin cambiar III)
hay un máximo local.

$\textcolor{Red}{\textbf{Diferencial de orden n}}$

$$d^{n}f=\frac{\partial^{n} f}{\partial x^{n}}dx^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}dx^{n-1}dy+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}dx^{n-2}dy^{2}+\cdots+$$ $$\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}dx^{n-k}dy^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$
que se puede escribir
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

$\textbf{Ejercicio}$ Probar usando inducción
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

$\small{Solución.}$ Para n=1 se tiene
$$df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy$$
Suponemos valido para n

$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$
Por demostrar que es valida para n+1
$$d^{n+1}f=d(d^{n}f)=\frac{\partial}{\partial x}\left(\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}\right)dx+\frac{\partial}{\partial y}\left(\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}\right)dy=$$

$$\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n-j}\partial y^{j+1}}dx^{n-j}dy^{j+1}=$$
$$\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\sum_{j=1}^{n+1}\left(\begin{matrix}n\\j-1\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}=$$

$$\frac{\partial^{n+1}f}{\partial x^{n+1}}dx^{n+1}+\sum_{j=1}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\sum_{j=1}^{n}\left(\begin{matrix}n\\j-1\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\frac{\partial^{n+1}f}{\partial y^{n+1}}dy^{n+1}=$$

$$\frac{\partial^{n+1}f}{\partial x^{n+1}}dx^{n+1}+\sum_{j=1}^{n}\left(\left(\begin{matrix}n\\j\end{matrix}\right)+\left(\begin{matrix}n\\j-1\end{matrix}\right)\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\frac{\partial^{n+1}f}{\partial y^{n+1}}dy^{n+1}=$$

$$\frac{\partial^{n+1}f}{\partial x^{n+1}}dx^{n+1}+\sum_{j=1}^{n}\left(\begin{matrix}n+1\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\frac{\partial^{n+1}f}{\partial y^{n+1}}dy^{n+1}=\sum_{j=0}^{n+1}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

La última fórmula puede expresarse simbólicamente por la ecuación
$$d^{n}f=\left(\frac{\partial}{\partial x}dx+\frac{\partial}{\partial y}dy\right)^{n}f$$

donde primero debe desarrollarse le expresión de la derecha formalmente por medio del teorema del binomio y, a continuación deben sustituirse los términos
$$\frac{\partial^{n}f}{\partial x^{n}}dx^{n},\frac{\partial^{n}f}{\partial x^{n-1}\partial y}dx^{n-1}dy,\cdots,\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$
por los términos
$$\left(\frac{\partial}{\partial x}dx\right)^{n}f,\left(\frac{\partial}{\partial x}dx\right)^{n-1}\left(\frac{\partial}{\partial y}dy\right)f,\cdots,\left(\frac{\partial}{\partial y}dy\right)^{n}f$$

$\textcolor{Red}{\textbf{Teorema de Taylor para funciones $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$}}$

Recordando el $\textcolor{Red}{\text{Teorema de Taylor para funciones $f:\mathbb{R}\rightarrow\mathbb{R}$}}$

$\textbf{Teorema.-}$ Si $f(x)$ tiene n-ésima derivada continua en una vecindad de $x_{0}$, entonces en esa vecindad
$$f(x)=f(x_{0})+\frac{1}{1!}f'(x_{0})(x-x_{0})+\frac{1}{2!}f»(x_{0})(x-x_{0})^{2}+\frac{1}{3!}f»'(x_{0})(x-x_{0})^{3}+…+\frac{1}{n!}f^{n}(x_{0})(x-x_{0})^{n}+R_{n}$$
donde
$$R_{n}=\frac{f^{n+1}(\epsilon)}{(n+1)!}(x-x_{0})^{n+1},~donde~\epsilon\in(x_{0},x)$$

Sea $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ y sea $F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t)$ con $t\in[0,1]$, de esta manera f recorre el segmento de $[x_{0},y_{0}]$ a $[x_{0}+h_{1}t,y_{0}+h_{2}t]$. Se tiene entonces que usando la regla de la cadena
$$F'(t)=\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot \frac{d(x_{0}+h_{1}t)}{dt}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot \frac{d(y_{0}+h_{2}t)}{dt}=$$

$$\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot h_{1}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot h_{2}$$
Vamos ahora a calcular $F^{´´}(t)$

$$F^{´´} ( t )=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}\right)h_{1}+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}\right)h_{2}=$$
$$\frac{\partial^{2} f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}h_{2}^{2}$$

simbólicamente se puede escribir
$$F^{»}(t)=\left(\frac{\partial }{\partial x}\cdot h_{1}+\frac{\partial }{\partial y}\cdot h_{2}\right)^{2}f$$
y en general

$$F^{n}(t)=\frac{\partial^{n} f}{\partial x^{n}}h_{1}^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}h_{1}^{n-1}h_{2}+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}h_{1}^{n-2}h_{2}^{2}+\cdots+\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}h_{1}^{n-k}h_{2}^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}h_{2}^{n}$$

que simbólicamente se puede escribir
$$F^{n}=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}h_{1}^{n-j}h_{2}^{j}=\left(\frac{\partial }{\partial x}\cdot h_{1}+\frac{\partial }{\partial y}\cdot h_{2}\right)^{n}f$$

Ahora bien si se aplica la fórmula de Taylor con la forma del residuo de Lagrange a la función $$F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t)$$ y ponemos $t=0$, se tiene
$$F(t)=F(0)+\frac{1}{1!}F'(0)t+\frac{1}{2!}F^{»}(0)t^{2}+\frac{1}{3!}F»'(0)t^{3}+…++\frac{1}{n!}F^{^{n}}(0)t^{n}+R_{n}$$
ahora bien con $t=1$
$$f(x_{0}+h_{1},y_{0}+h_{2})=f(x_{0},y_{0})+\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot h_{2}\right)+\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})h_{2}^{2}\right)$$
$$+\cdots+\frac{1}{n!}\left(\sum_{j=0}^{n+1}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}(x_{0},y_{0})h_{1}^{n-j}h_{2}^{j}\right)$$

$x=x_{0}+h_{1}$, $y_{0}+h_{2}=y$ por lo que $h_{1}=x-x_{0}$ y $h_{2}=y-y_{0}$ entonces

$$f(x,y)=f(x_{0},y_{0})+\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)+$$

$$\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})(x-x_{0})^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})(x-x_{0})(y-y_{0})+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})(y-y_{0})^{2}\right)+$$

$$\cdots+\frac{1}{n!}\left(\sum_{j=0}^{n+1}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}(x_{0},y_{0})(x-x_{0})^{n-j}(y-y_{0})^{j}\right)+R_{n}$$

donde
$$R_{n}=\frac{1}{n+1!}\left((x-x_{0})^{n+1}\frac{\partial^{n+1}f}{\partial x^{n+1}}(\xi,\eta)+\cdots+(y-y_{0})^{n+1}\frac{\partial^{n+1}f}{\partial y^{n+1}}(\xi,\eta)\right)$$ donde $\xi\in(x_{0},x_{0}+h_{1})$ y $\eta\in(y_{0},y_{0}+h_{2})$\En general el residuo $R_{n}$ se anula en un orden mayor que el término $d^{n}f$

$\textbf{Ejemplo}$ Desarrollar la fórmula de Taylor en $(x_{0},y_{0})=(0,0)$ con $n=3$ para la función $$f(x,y)=e^{y}\cos x$$

$\small{Solución.}$

En este caso tenemos que
$$f(0,0)=e^{0}\cos(0)=1$$
Para la diferencial de orden 1
$$\frac{\partial f}{\partial x}(0,0)~\Rightarrow~\frac{\partial (e^{y}\cos(x))}{\partial x}(0,0)~\Rightarrow~-e^{y} sen\left( x\right) \big{|}{(0,0)}=0$$ $$\frac{\partial f}{\partial y}(0,0)~\Rightarrow~\frac{\partial (e^{y} \cos x)}{\partial y}(0,0)~\Rightarrow~-e^{y}\cos(x)\big{|}{(0,0)}=1$$
por lo tanto
$$\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)=\frac{1}{1!}\left((0)(x)+(1)(y)\right)=y$$
Para la diferencial de orden 2
$$\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\ cos x)}{\partial x^{2}}(0,0)~\Rightarrow~-e^{y} \cos~x\big{|}{(0,0)}=-1$$ $$\frac{\partial^{2} f}{\partial y^{2}}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y} \cos x)}{\partial y^{2}}(0,0)~\Rightarrow~e^{y} \cos~x\big{|}{(0,0)}=1$$ $$\frac{\partial^{2} f}{\partial x~\partial y}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial x~\partial y}(0,0)~\Rightarrow~-e^{y} sen~x~ \big{|}{(0,0)}=0$$ Por lo tanto $$\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x{0},y_{0})h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})h_{2}^{2}\right)=\frac{1}{2!}((-1)x^{2}+2(0)xy+(1)y^{2})$$
Para la diferencial de orden 3

$$\frac{\partial^{3} f}{\partial x^{3}}(x_{0},y_{0})~\Rightarrow~e^{y} sen~x\big{|}_{(0,0)}=0$$

$$\frac{\partial^{3} f}{\partial y^{3}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial y^{3}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(0,0)}=1$$

$$\frac{\partial^{3} f}{\partial x^{2}~\partial y}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial x^{2}~\partial y}(0,0)~\Rightarrow~-e^{y}\cos~x\big{|}_{(0,0)}=-1$$

$$\frac{\partial^{3} f}{\partial y^{3}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial y^{3}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(0,0)}=1$$

$$\frac{\partial^{3} f}{\partial x~\partial y^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial x~\partial y^{2}}(0,0)~\Rightarrow~-e^{y} sen~x\big{|}_{(0,0)}=0$$

Por lo tanto
$$\frac{1}{3!}\left(\frac{\partial^{3} f}{\partial x^{3}}h_{1}^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}h_{}1^{2}h_{2}+3\frac{\partial^{3} f}{\partial x\partial y^{2}}h_{1}h_{2}^{2}+\frac{\partial^{3} f}{\partial y^{3}}h_{}2^{3}\right)=$$

$$\frac{1}{3!}\left((0)(x^{3})+3(-1)x^{2}y+3(0)xy^{2}+(1)y^{3}\right)$$
Finalmente para el residuo se tiene

$$\frac{\partial^{4} f}{\partial x^{4}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos(x))}{\partial y^{3}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(\xi,\eta)}=e^{\eta}\cos~\xi$$

$$\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos x)}{\partial x^{2}\partial y^{2}}(0,0)~\Rightarrow~-e^{y}\cos~x\big{|}_{(\xi,\eta)}=-e^{\eta}\cos~\xi$$

$$\frac{\partial^{4} f}{\partial x\partial y^{3}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos x)}{\partial x\partial y^{3}}(0,0)~\Rightarrow~-e^{y} sen~x\big{|}_{(\xi,\eta)}=-e^{\eta} sen~\xi$$

$$\frac{\partial^{4} f}{\partial y^{4}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos x)}{\partial y^{4}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(\xi,\eta)}=e^{\eta}\cos~\xi$$

$$R_{3}=\frac{1}{4!}\left(\frac{\partial^{4} f}{\partial x^{4}}h_{1}^{4}+4\frac{\partial^{4} f}{\partial x^{3}\partial y}h_{1}^{3}h_{2}+6\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}h_{1}^{2}h_{2}^{2}+4\frac{\partial^{4} f}{\partial x\partial y^{3}}h_{1}h_{2}^{3}+\frac{\partial^{4} f}{\partial h_{2}^{4}}dy^{4}\right)$$

$$=\frac{1}{4!}\left(x^{4}e^{\eta}\cos~\xi+4x^{3}ye^{\eta} sen~xi-6x^{2}y^{2}e^{\eta}\cos~\xi-4xy^{3}e^{\eta} sen~\xi+y^{4}e^{\eta}\cos~\xi\right)$$

Por lo que nuestro desarrollo de Taylor nos queda
$$e^{y}\cos~x=1+y+\frac{1}{2}(x^{2}-y^{2})+\frac{1}{6}(x^{3}-3xy^{2})+R_{3}$$
donde
$$R_{3}=\frac{1}{4!}\left(x^{4}e^{\eta}\cos~\xi+4x^{3}ye^{\eta} sen~xi-6x^{2}y^{2}e^{\eta}\cos~\xi-4xy^{3}e^{\eta} sen~\xi+y^{4}e^{\eta}\cos~\xi\right)$$
$\textbf{Ejercicio}$ Use la fórmula de Taylor en
$$f(x,y)=\cos~(x+y)$$
en el punto $(x_{0},y_{0})=(0,0)$ con $n=2$ para comprobar que
$$\lim_{(x,y)\rightarrow(0,0)}\frac{1-\cos~(x+y)}{(x^{2}+y^{2})^{2}}=\frac{1}{2}$$

En este caso para
$$f(x,y)=\cos(x+y)$$
se tiene
$$f(0,0)=\cos(0+0)=1$$
Para la diferencial de orden 1
$$\frac{\partial f}{\partial x}(0,0)~\Rightarrow~\frac{\partial (\cos x+y)}{\partial x}(0,0)~\Rightarrow~- sen(x+y)\big{|}{(0,0)}=0$$ $$\frac{\partial f}{\partial y}(0,0)~\Rightarrow~\frac{\partial (\cos x+y)}{\partial y}(0,0)~\Rightarrow~- sen(x+y)\big{|}{(0,0)}=0$$
por lo tanto

$$\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)=\frac{1}{1!}\left((0)(x)+(0)(y)\right)=0$$

Para la diferencial de orden 2
$$\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (\cos x+y)}{\partial x^{2}}(0,0)~\Rightarrow~-\cos~x+y\big{|}{(0,0)}=-1$$ $$\frac{\partial^{2} f}{\partial y^{2}}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (\cos x+y)}{\partial y^{2}}(0,0)~\Rightarrow~-\cos~x+y\big{|}{(0,0)}=-1$$ $$\frac{\partial^{2} f}{\partial x~\partial y}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (\cos x+y)}{\partial x~\partial y}(0,0)~\Rightarrow~-\cos~x+y\big{|}_{(0,0)}=-1$$
Por lo tanto

$$\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})h_{2}^{2}\right)=\frac{1}{2!}((-1)x^{2}-2xy+(-1)y^{2})$$
Por lo que nuestro desarrollo de Taylor nos queda
$$\cos(x+y)=1-\frac{x^{2}}{2}-xy-\frac{y^{2}}{2}$$
De manera que

$$\lim_{(x,y)\rightarrow(0,0)}\frac{1-\cos~(x+y)}{(x^{2}+y^{2})^{2}}=\lim_{(x,y)\rightarrow(0,0)}\frac{1-(1-\frac{x^{2}}{2}-xy-\frac{y^{2}}{2})}{(x^{2}+y^{2})^{2}}$$
$$=\lim_{(x,y)\rightarrow(0,0)}\frac{1}{2}\frac{(x^{2}+y^{2})^{2}}{(x^{2}+y^{2})^{2}}=\frac{1}{2}$$

$\textcolor{Red}{\textbf{Derivadas Parciales de Orden Superior}}$

Si $f$ es una función de doas variables $x,y$ $\Rightarrow$ $\displaystyle\frac{\partial f}{\partial x}, \displaystyle\frac{\partial f}{\partial y}$ son funciones de las mismas variables, cuando derivamos $\displaystyle\frac{\partial f}{\partial x}$ y $ \displaystyle\frac{\partial f}{\partial y}$ obtenemos las derivadas parciales de segundo orden, las derivadas de $\displaystyle\frac{\partial f}{\partial x}$ están definidas por:

$$\displaystyle\frac{\partial^{2}f}{\partial x^{2}}(x,y)=\displaystyle\lim_{h\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x+h,y)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{h}}$$

$$\displaystyle\frac{\partial^{2}f}{\partial y \partial x}(x,y)=\displaystyle\lim_{k\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x,y+k)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{k}}$$

Si $f$ es una función de dos variables entonces hay cuatro derivadas parciales de segundo orden.

Consideremos las diferentes notaciones para las derivadas parciales:

$$f_{1,1}=\displaystyle\frac{\partial^{2}f}{\partial x^{2}}=f_{xx}$$

$$f_{1,2}=\displaystyle\frac{\partial^{2}f}{\partial y \partial x}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial x}\bigg)=f_{xy}$$

$$f_{2,1}=\displaystyle\frac{\partial^{2}f}{\partial x \partial y}=\frac{\partial}{\partial x}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yx}$$

$$f_{2,2}=\displaystyle\frac{\partial^{2}f}{\partial y^{2}}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yy}$$

$\textbf{Ejemplo.}$ $z=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$ hallar $\displaystyle\frac{\partial z}{\partial x}, \displaystyle\frac{\partial z}{\partial y},\displaystyle\frac{\partial^{2} z}{\partial x^{2}},\displaystyle\frac{\partial^{2}z}{\partial x \partial y},\displaystyle\frac{\partial^{2}z}{\partial y \partial x},\displaystyle\frac{\partial^{2} z}{\partial y^{2}}$

$$\displaystyle\frac{\partial z}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$

$$\displaystyle\frac{\partial z}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$

$$\displaystyle\frac{\partial^{2} z}{\partial x^{2}}=6x+6y-4y^{2}$$

$$\displaystyle\frac{\partial^{2} z}{\partial y^{2}}=-4x^{2}-12y^{2}$$

$$\displaystyle\frac{\partial^{2}z}{\partial y \partial x}=6x-8xy+3$$

$$\displaystyle\frac{\partial^{2}z}{\partial x \partial y}=6x-8xy+3$$

$\textbf{Teorema 1.}$ $\textcolor{Red}{\textbf{Teorema de schwarz}}$

Sea $f:A\subset \mathbb{R}^{2}\rightarrow\mathbb{R}$ una función definida en el abierto A de $\mathbb{R}^{2}$. Si las derivadas parciales

$$\frac{\partial^{2} f}{\partial y\partial x}~y~\frac{\partial^{2} f}{\partial x\partial y}$$

existen y son continuas en $A$, entonces

$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} f}{\partial x\partial y}$$

$\small{Demostración.}$ Sea

$\displaystyle{M=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-f(x,y+h_{2})+f(x,y)}$ y definimos $$\varphi(x)=f(x,y+h_{2})-f(x,y)$$de manera que
$$\varphi(x+h_{1})-\varphi(x)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$

Aplicando el TVM a $\varphi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\theta~\in~(x,x+h_{1})$ tal que

$$\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}$$

por otro lado
$$\varphi'(x)=\frac{\partial f}{\partial x}(x,y+h_{2})-\frac{\partial f}{\partial x}(x,y)$$
por lo tanto
$$\varphi'(\theta)=\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)$$
tenemos entonces que

$$M=\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}$$
Consideremos ahora $\displaystyle{\psi(y)=\frac{\partial f}{\partial x}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\eta~\in~(y,y+h_{2})$ tal que
$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}$$
por otro lado

$$\psi'(y)=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right)(x,y)=\frac{\partial^{2}f}{\partial y\partial x}(x,y)$$
por lo tanto
$$\psi'(\eta)=\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)$$
de esta manera

$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}=\left(\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)\right)h_{2}$$
y si $\theta\in (x,x+h_{1})$ tenemos entonces que

$$\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}$$
en consecuencia
$$M=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}$$

Consideremos ahora $$\overline{\varphi}(y)=f(x+h_{1},y)-f(x,y)$$de manera que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$

Aplicando el TVM a $\overline{\varphi}$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\overline{\eta}~\in~(y,y+h_{2})$ tal que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}$$
por otro lado
$$\overline{\varphi}'(y)=\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)$$
por lo tanto

$$\overline{\varphi}'(\overline{\eta})=\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})$$
tenemos entonces que
$$M=\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{2}$$

Consideremos ahora $\displaystyle{\overline{\psi}(x)=\frac{\partial f}{\partial y}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\overline{\theta}~\in~(x,x+h_{1})$ tal que
$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}$$
por otro lado

$$\overline{\psi}'(x)=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right)(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$
por lo tanto
$$\overline{\psi}'(\overline{\theta})=\frac{\partial^{2}f}{\partial y\partial x}(\overline{\theta},y)$$
de esta manera

$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
es decir
$$\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
y si $\overline{\eta}\in (y,y+h_{2})$ tenemos entonces que
$$\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{1}$$
en consecuencia

$$M=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{1}h_{2}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
igualando ambas expresiones de M se tiene
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
donde
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)$$
Tomando limite cuando $h_{1},h_{2}\rightarrow 0$ y usando la continuidad asumida de las parciales mixtas se tiene que $\theta,\overline{\theta}\rightarrow x$ y $\eta,\overline{\eta}\rightarrow y$ se concluye
$$\frac{\partial^{2}f}{\partial y\partial x}(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$ $\square$

$\textbf{Ejemplo}$

Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$\
En este caso
$$\frac{\partial f}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$
$$\frac{\partial f}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$
$$\frac{\partial^{2} f}{\partial x^{2}}=6x+6y-4y^{2}$$
$$\frac{\partial^{2} f}{\partial y^{2}}=-4x^{2}-12y^{2}$$
$$\frac{\partial^{2} f}{\partial x\partial y}=6x-8xy+3$$
$$\frac{\partial^{2} f}{\partial y\partial x}=6x-8xy+3$$
$\textbf{Ejemplo.}$ Dada la función

tenemos que para $(x,y)\neq (0,0)$
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
$$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
para el primer caso hacemos $x=0$ y tenemos
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{x=0}-y$$ para el segundo caso hacemos $y=0$ y tenemos $$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{y=0}1$$
Calculamos ahora
$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} (-y)}{\partial y\partial x}=-1$$
$$\frac{\partial^{2} f}{\partial x\partial y}=\frac{\partial^{2} (1)}{\partial x\partial y}=1$$
por lo tanto
$$\frac{\partial^{2} f}{\partial y\partial x}=-1\neq 1=\frac{\partial^{2} f}{\partial x\partial y}$$
En este caso las parciales segundas no son contiuas en $(0,0)$

$\textbf{Teorema.}$ $\textcolor{Red}{\textbf{Caso General}}$

Sea $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ definida en el abierto A de $\mathbb{R}^{n}$ tal que
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}$$ sean continuas en A, entonces
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}=\frac{\partial^{2} f}{\partial x_{j}\partial x_{i}}$$

$\textcolor{Red}{\textbf{Caso particular de la regla de la cadena}}$

Supongamos que $C:\mathbb{R}\rightarrow\mathbb{R}^{3}$ es una trayectoria diferenciable y $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$.

Sea $h(t)$=$f(x(t), y(t), z(t))$ donde $c(t)$=$(x(t),y(t), z(t))$.
Entonces

$$\displaystyle\frac{\partial{h}}{\partial{t}} = \displaystyle\frac{\partial{f}}{\partial{x}}\cdot \frac{\partial{x}}{\partial{t}}+\frac{\partial{f}}{\partial{y}}\cdot
\frac{\partial{y}}{\partial{t}}+\frac{\partial{f}}{\partial{z}}\cdot
\frac{\partial{z}}{\partial{t}}$$

Esto es:
$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\nabla{f(c(t))}\cdot
{c'(t)}$, ~donde $c'(t)$=$((x'(t), y'(t), z'(t))$

$\small{Dem.}$ Por definición
$\displaystyle\frac{\partial{h}}{\partial{t}}(t_{0})$=$\displaystyle\lim_{t\rightarrow0}\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$
Sumando y restando tenemos que

$\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$=$\displaystyle\frac{f(c(t))-f(c(t_{0}))}{t-t_{0}}$=$\displaystyle\frac{f(x(t), y(t), z(t)) – f(x(t_{0}), y(t_{0}), z(t_{0}))}{t-t_{0}}$=

=$\frac{f(x(t), y(t), z(t))~-~f(x(t_{0}), y(t),
z(t))~+~f(x(t_{0}), y(t), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t))~+~f(x(t_{0}), y(t_{0}), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t_{0}))}{t-t_{0}}$…$\ast$

Aplicando el Teorema del valor medio $\textbf{(T.V.M.)}$

$f(~x(t),~y(t),~z(t))-f(~x(t_{0}),~y(t),~z(t))=\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~(x(t)-x(t_{0}))$

$f(~x(t_{0}),~y(t),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t))=\displaystyle\frac{\partial{f}}{\partial{y}}~(x(t),~ d, ~z(t))~(y(t)-y(t_{0}))$

$f(~x(t_{0}),~y(t_{0}),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t_{0}))=\displaystyle\frac{\partial{f}}{\partial{z}}(~x(t),~y(t),~e)~(z(t)-z(t_{0}))$

$\therefore$$\ast$=$\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~\displaystyle\frac{x(t)-x(t_{0})}{t-t_{0}}+\displaystyle\frac{\partial{f}}{\partial{y}}~(~x(t),~d,~z(t))~\displaystyle\frac{y(t)-y(t_{0})}{t-t_{0}}$+

$+\displaystyle\frac{\partial{f}}{\partial{z}}~(~x(t),~y(t),~e))~\displaystyle\frac{z(t)-z(t_{0})}{t-t_{0}}$

Tomando $\displaystyle\lim_{t\rightarrow{t_{0}}}$ y por la continuidad de las parciales

$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\displaystyle\frac{\partial{f}}{\partial{x}}~\frac{\partial{x}}{\partial{t}}+ \displaystyle\frac{\partial{f}}{\partial{y}}~\frac{\partial{y}}{\partial{t}}+\displaystyle\frac{\partial{f}}{\partial{z}}~\frac{\partial{z}}{\partial{t}}$

$\textcolor{Red}{\textbf{Ejemplos: Caso particular de la regla de la cadena}}$

$\textbf{Ejemplo.}$ Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+3y^{2}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$

$\small{Solución.}$En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=2x\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=2e^{t}\cdot e^{t}=2e^{2t}$$

$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (\cos(t))}{dt}=6y\left|{(e^{t},\cos(t))}\cdot (-sen(t))\right.=6 cos(t) \cdot (- sen(t))$$
por lo tanto
$$h'(t)=2e^{2t}-6\cos(t)\cdot (sen(t))$$

$\textbf{Ejemplo.}$ Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=xy$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$

$\small{Solución.}$

En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (xy)}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=y\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=\cos(t)\cdot e^{t}$$

$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (xy)}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (cos(t))}{dt}=x\left|{(e^{t},cos(t))}\cdot (-sen(t))\right.=e^{t}\cdot (-sen(t))$$

por lo tanto
$$h'(t)=\cos(t)e^{t}-e^{t}\cdot sen(t)$$

$\textbf{Ejemplo.}$ Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=e^{xy}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(3t^{2},t^{3})$

$\small{Solución}$ En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene

$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial x}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (3t^{2})}{dt}=ye^{xy}\left|{(3t^{2},t^{3})}\cdot 6t\right.=t^{3}e^{3t^{5}}6t=6t^{4}e^{3t^{5}}$$

$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial y}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (t^{3})}{dt}=xe^{xy}\left|{(3t^{2},t^{3})}\cdot 3t^{2}\right.=3t^{2}e^{3t^{5}}3t^{2}=9t^{4}e^{3t^{5}}$$
por lo tanto
$$h'(t)=6t^{4}e^{3t^{5}}+9t^{4}e^{3t^{5}}=15t^{4}e^{3t^{5}}$$

$\textbf{Teorema 1.}$

El gradiente es normal a las superficies de nivel. Sea $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ una aplicación $C^{1}$ y sea
$(x_{0},y_{0},z_{0})$ un punto sobre la superficie de nivel $S$ definida por $f(x,y,z)$=$k$, $k$=$cte$. Entonces $\nabla{f}(x_{0},~y_{0},~z_{0})$ es normal a la superficie de nivel en el siguiente sentido: si $v$ es el vector tangente en $t$=$t_{0}$ de
una trayectoria $c(t)$ con $c(t_{0})$=$(x_{0},~y_{0},~z_{0})$ Entonces $\nabla{f}\cdot {v}$=$0$

que se puede escribir como
$$\left(\frac{\partial f}{\partial x}(x(t),y(t)z(t)),\frac{\partial f}{\partial y}(x(t),y(t)z(t)),\frac{\partial f}{\partial z}(x(t),y(t)z(t))\right)\cdot\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)=0$$
en $t=t_{0}$
$$\nabla f(x(0),y(0),z(0))\cdot c'(t_{0})=0$$

$\textcolor{Red}{\textbf{Plano Tangente}}$

Sea $f:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}$ una función diferenciable definida en A, y sea
$$S={(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c}$$

una superficie de nivel de f y $\hat{x}{0}=(x{0},y_{0},z_{0})$ un punto de ella. Considere además, una curva
$$\alpha(t)=(x(t),y(t),z(t))$$
y una curva
$$\beta(t)=(x_{1}(t),y_{1}(t),z_{1}(t))$$

que pasen por $\hat{x}{0}$ con $t\in[a,b]$ en ambos casos y tanto $\alpha$ como $\beta$ diferenciables, se tiene entonces $$(f\circ\alpha)'(t)=f'(\alpha(t))\alpha'(t)=\nabla f(\alpha(t))\cdot \alpha'(t)=0$$ $$(f\circ\beta)'(t)=f'(\beta(t))\beta'(t)=\nabla f(\beta(t))\cdot \beta'(t)=0$$ pues el gradiente $\nabla f(\hat{x}{0})$ en ambos casos es ortogonal tanto al vector $\alpha'(t_{0})$ como al vector $\beta'(t_{0})$ en el punto $\hat{x_{0}}=\alpha(t_{0})=\beta(t_{0})$

Si $\nabla f(\hat{x}{0})\neq 0$, entonces las tangentes a las curvas $\alpha, \beta$ sobre S que pasan por $\hat{x}{0}$

están contenidas en un mismo plano; por lo que el plano tangente a
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c \right\}$$ se define

$\textbf{Definición}$ El plano tangente a S en $\hat{x}{0}$ se define $$P={\hat{x}~|~\nabla f(\hat{x}{0})\cdot (\hat{x}-\hat{x}_{0})=0}$$

$\textbf{Ejemplo.}$ Hallar el plano tangente a la superficie
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~\frac{x^{2}}{4}-\frac{y^{2}}{9}+z^{2}=1 \right\}$$
en el punto $(2,3,1)$

$\small{Solución.}$

En este caso el gradiente es
$$\nabla f(x,y,z)=\left(\frac{x}{2},-\frac{2}{9}y,2z\right)$$
en el punto $(2,3,1)$ es
$$\nabla f(2,3,1)=\left(1,-\frac{2}{3},2\right)$$
Por tanto la ecuación del plano tangente es
$$\left(1,-\frac{2}{3},2\right)\cdot (x-1,y-3,z-1)=0$$
es decir
$$3x-2y+6z-6=0$$

$\textcolor{Red}{\textbf{Diferenciabilidad de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}}$

$\textbf{Definición.}$ Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x}(x_{0},y_{0}),~~\frac{\partial f}{\partial y}}(x_{0},y_{0})$ tal que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$

$\textcolor{Red}{\textbf{Diferenciabilidad implica continuidad de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}}$

$\textbf{Teorema 1.}$ Si la función $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ definida en $A$ de $\mathbb{R}^{2}$, es diferenciable en el ´punto $p=(x_{0},y_{0})\in A$, entonces es continua en ese punto.

$\small{Demostración.}$ Si f es diferenciable en el ´punto $p=(x_{0},y_{0})\in A$ se tiene
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
tomando limite se tiene
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}f((x_{0},y_{0})+(h_{1},h_{2}))=\lim_{(h_{1},h_{2})\rightarrow(0,0)}f(x_{0},y_{0})+\cancel{\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}}+\cancel{\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}}+\cancel{r(h_{1},h_{2})}$$
se tiene entonces que
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})$$
por lo que f es continua en $(x_{0},y_{0})$

$\textcolor{Red}{\textbf{Aplicacion del Teorema del Valor Medio de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}}$

$\textbf{Teorema 2.}$ Suponga que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es tal que
$$\left|\frac{\partial f}{\partial x}(x_{0},y_{0})\right|\leq M$$ y $$\left|\frac{\partial f}{\partial x}(x_{0},y_{0})\right|\leq M$$

donde $M$ no depende de $x,y$ entonces $f$ es continua en $A$.

$\small{Demostración.}$ Sean $(x_{0},y_{0}),(x_{0}+h_{1},y_{0}+h_{2})\in A$ tenemos entonces que $$f(x_{0}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=f(x_{0}+h_{1},y_{0}+h_{2})\textcolor{Red}{-f(x_{0}+h_{1},y_{0})+f(x_{0}+h_{1},y_{0})}-f(x_{0},y_{0})$$ Aplicando teorema del valor medio se tiene que existen $\xi_{1},\in\ (x_{0},x_{0}+h_{1})$,$\xi_{2}\in(y_{0},y_{0}+h_{2})$ tal que $$f(x_{0}+h_{1},y_{0}+h_{2})\textcolor{Red}{-f(x_{0}+h_{1},y_{0})}=\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})h_{2}$$ $$\textcolor{Red}{f(x_{0}+h_{1},y_{0})}-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2})h_{1}$$ por lo tanto $$\left|f(x_{0}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})\right|=\left|\left(\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})h_{2}\right)+\left(\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2})h_{1}\right)\right|\leq $$ $$\left|\left(\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})\right)\right||h_{2}|+\left|\left(\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2}\right)\right|)|h_{1}|\leq M(|h_{2}|+|h_{1}|)$$ si tenemos que $\displaystyle{|(h_{1},h_{2})|}<\delta$ entonces $$M(|h_{2}|+|h_{1}|)<2M\delta~\therefore~~~\epsilon=2M\delta\Rightarrow \delta=\frac{\epsilon}{2M}$$

$\textcolor{Red}{\textbf{Diferenciabilidad y Derivadas Direccionales}}$

$\textbf{Teorema 3.}$ Si $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ es una función diferenciable en $x_{0}$ en la dirección del vector unitario u entonces
$$\frac{\partial f}{\partial u}(x_{0})=\sum_{i=1}^{n}\frac{\partial~f}{\partial x_{i}}\cdot u_{i}$$

$\small{Demostración.}$

Sea $u\in\mathbb{R}^{n}$ tal que $u\neq0$ y $|u|=1$ como $f$ es diferenciable en
$x_{0}$, se tiene que
$$f(x_{0}+h)-f(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})h_{i}+r(h)$$satisface
$$\lim_{(h)\rightarrow 0}\frac{r(h)}{|(h)|}=0$$
tomando $h=tu$ se tiene $|h|=|tu|=|t||u|=|t|$\
se tiene entonces
$$f(x_{0}+t(u))-f(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})tu_{i}+r(tu)$$
tenemos entonces
$$\lim_{t\rightarrow0}\frac{f(x_{0}+t(u))-f(x_{0})}{t}=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})u_{i}+\cancel{\lim_{t\rightarrow0}r(tu)}$$
es decir
$$\frac{\partial f}{\partial u}(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})u_{i}$$ $\square$

$\textbf{Ejemplo.}$ Halle la derivada direccional de $f(x,y)=\ln(x^{2}+y^{3})$ en el punto $(1,-3)$ en la dirección $(2,-3)$

$\small{Solución.}$

En este caso
$$u=(2,-3)~\Rightarrow~|u|=\sqrt{13}~\rightarrow~\frac{u}{|u|}=\left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)$$

$$\frac{\partial f}{\partial x}(1,-3)=\frac{2x}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-2}{26}$$

$$\frac{\partial f}{\partial y}(1,-3)=\frac{3y^{2}}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-27}{26}$$

por lo tanto
$$D_{\left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)}f\left(1,-3\right)=\left(\frac{-2}{26}\right)\cdot\left(\frac{2}{\sqrt{13}}\right)+\left(\frac{-27}{26}\right)\cdot \left(\frac{-3}{\sqrt{13}}\right)=\frac{77\sqrt{13}}{338}$$

$\textcolor{Red}{\textbf{El Gradiente}}$

Sea $f:A\subset \mathbb{R}^{n}\rightarrow \mathbb{R}$ una función diferenciable en $x_{0}\in A$. Entonces el vector cuyas componentes
son las derivadas parciales de f en $x_{0}$ se le denomina Vector Gradiente
$$\left(\frac{\partial f}{\partial x_{1}}(x_{0}),\frac{\partial f}{\partial x_{2}}(x_{0}),…,\frac{\partial f}{\partial x_{n}}(x_{0}),\right)$$
y se le denota por $\nabla f$.

En el caso particular $n=2$ se tiene
$$\nabla f(x_{0})=\left(\frac{\partial f}{\partial x}(x_{0}),\frac{\partial f}{\partial y}(x_{0})\right)$$
En el caso particular $n=3$ se tiene
$$\nabla f(x_{0})=\left(\frac{\partial f}{\partial x}(x_{0}),\frac{\partial f}{\partial y}(x_{0}),\frac{\partial f}{\partial z}(x_{0})\right)$$

$\textbf{Ejemplo.}$ Calcular $\nabla f$ para $f(x,y)=x^{2}y+y^{3}$
$\small{Solución}$En este caso
$$\nabla f(x,y)=\left(2xy,x^{2}+3y^{2}\right)$$

$\textbf{Teorema 4.}$ Si $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ es una función diferenciable en $(x_{0},y_{0})$ en la dirección del vector unitario u entonces
$$\frac{\partial f}{\partial u}(x_{0},y_{0})=\nabla f(x_{0},y_{0})\cdot u$$

Sea $u\in\mathbb{R}^{n}$ tal que $u\neq0$ y $|u|=1$ como $f$ es diferenciable en
$(x_{0},y_{0})$, se tiene que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$

satisface
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
tomando $h=tu$ se tiene $|h|=|(h_{1},h_{2})|=|tu|=|t||u|=|t|$

se tiene entonces
$$f((x_{0},y_{0})+t(u))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})tu_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})tu_{2}+r(tu_{1},ru_{2})$$
y también
$$\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=\frac{r(tu_{1},ru_{2})}{|tu|}=\frac{r(tu_{1},ru_{2})}{|t||u|}=\frac{r(tu_{1},ru_{2})}{|t|}$$
tenemos entonces
$$\lim_{t\rightarrow0}\frac{r(tu_{1},ru_{2})}{|t|}=\lim_{t\rightarrow0}\frac{f((x_{0},y_{0})+t(u))-f(x_{0},y_{0})}{|t|}-\frac{\frac{\partial f}{\partial x}(x_{0},y_{0})tu_{1}}{|t|}-\frac{\frac{\partial f}{\partial y}(x_{0},y_{0})tu_{2}}{|t|}$$
es decir
$$0=\frac{\partial f}{\partial u}(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})u_{1}-\frac{\partial f}{\partial y}(x_{0},y_{0})u_{2}$$
y en consecuencia

$$\frac{\partial f}{\partial u}(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})u_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})u_{2}=\left(\frac{\partial f}{\partial x}(x_{0},y_{0},\frac{\partial f}{\partial y}(x_{0},y_{0}\right)\cdot\left(u_{1},u_{2}\right)=\nabla f(x_{0},y_{0})\cdot u$$ $\square$

$\textbf{Ejemplo.}$ Halle la derivada direccional de $f(x,y)=\ln(x^{2}+y^{3})$ en el punto $(1,-3)$ en la dirección $(2,-3)$

$\small{Solución.}$ En este caso

$$\frac{\partial f}{\partial x}(1,-3)=\frac{2x}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-2}{26}$$

$$\frac{\partial f}{\partial y}(1,-3)=\frac{3y^{2}}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-27}{26}$$

por lo tanto
$$\nabla f(1,-3)=\left(\frac{-2}{26},\frac{-27}{26}\right)\cdot \left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)=\frac{77}{26\sqrt{13}}=\frac{77\sqrt{13}}{338}$$

$\textcolor{Red}{\textbf{Dirección de Mayor Crecimiento de una Función}}$

$\textbf{Teorema 5.}$ Supongamos que $\nabla(f(x))\neq(0,0,0)$. Entonces $\nabla(f(x))$ apunta en la dirección a lo largo de la cual f crece más rápido.

$\small{Demostración.}$ Si v es un vector unitario, la razón de
cambio de f en la dirección v está dada por $\nabla(f(x))\cdot v$ y
$\nabla(f(x)) \cdot v$ = $|\nabla{f(x)}|~|v|\cos\Theta$ = $|\nabla{f(x)}|\cos\Theta$,
donde $\Theta$ es el ángulo entre $\nabla{f}$, $v$. Este es máximo cuando $\Theta~=~0$ y esto ocurre cuando $v$, $~\nabla{f}$ son paralelos. En otras palabras, si queremos movernos en una dirección en la cual $f$ va a crecer más rápidamente, debemos proceder en la dirección $\nabla{f(x)}$. En forma análoga, si queremos movernos en la dirección en la cual $f$ decrece más rápido, habremos de proceder
en la dirección $-\nabla{f}$.

$\textbf{Ejemplo.}$ Encontrar la dirección de rapido crecimiento en $(1,1,1)$ para $\displaystyle{f(x,y,z)=\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}}$

$\small{Solución.}$ En este caso

$$\nabla f(1,1,1)=\left(\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial x},\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial y},\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial z}\right)\left|_{(1,1,1)}\right.=$$

$$\left(-\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}},-\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}},-\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)\left|_{(1,1,1)}\right.=-\frac{1}{3\sqrt{3}}\left(1,1,1\right)$$
Podemos tomar

$$u=\frac{\nabla f}{|\nabla f|}$$
en este caso
$$u=\frac{-\frac{1}{3\sqrt{3}}\left(1,1,1\right)}{\frac{1}{3}}=\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$$

$\textcolor{Red}{\textbf{Puntos Estacionarios}}$

$\textbf{Definición.}$ Sea $f:\Omega\subset \mathbb{R}^{n} \rightarrow \mathbb{R}$ diferenciable, a los puntos $x\in \Omega$ tales que $\nabla f(x)=0$ se les llama puntos críticos (o punto estacionario) de la función.

$\textbf{Ejemplo.}$ Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ hallar los puntos críticos de $f$

$\small{Solución.}$ Se tiene que $\nabla f(x)=(2x, 2y)$ \hspace{0.5cm}$\nabla f(x)=0\Leftrightarrow(2x, 2y)=(0,0)\Leftrightarrow 2x=0$ y $2y=0\Leftrightarrow x=0$ y $y=0$ \hspace{0.5cm} $\therefore$ $(0,0)$ es el único punto crítico de $f$.

$\textbf{Ejemplo.}$ Que condición se debe satisfacer para que la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=ax^{2}+2bxy+cy^{2}+dx-ey+f$ tenga un punto crítico

$\nabla f=(2ax+2by+d, 2bx+2cy-e)$ entonces

$\nabla f=0\Leftrightarrow 2ax+2by+d=0$ y $2bx+2cy-e=0$

$\Rightarrow$ $ 2ax+2by=-d$ y $2bx+2cy=e$ se necesita que

$\Rightarrow$ $2a(2c)-(2b)^{2}\neq 0$ $\therefore$ $ac-b^{2}\neq 0$