(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Éste es un momento emotivo. Hemos llegado a la última entrada del curso. Así que sin mucho preámbulo comencemos a hablar del tema que nos compete.

El Teorema de Jordan-Hölder nos dice que cada par de series de composición de un grupo $G$ siempre son del mismo tamaño y con factores de composición isomoforfos entre sí. De nuevo, es un teorema que nos describe cómo es un grupo y los subgrupos que lo conforman.

Debido a que los factores de composición son grupos simples, obtenemos una descomposición del grupo $G$ en elementos mínimos (en el sentido de que no tienen una subestructura del mismo tipo) y de nuevo, podemos hacer una analogía con el Teorema fundamental de la aritmética, aunque esto se ve mejor cuando $G = \z_n.$

Por último, así como el Cuarto teorema de isomorfía justifica que los factores de composición son simples, en la demostración del Teorema de Jordan-Hölder usamos mucho el Segundo teorema de isomorfía para justificar la isomorfía que existe entre los factores de composición, así que es recomendable repasarlo.

El último teorema del curso

Teorema. (de Jordan – Hölder) Sean $G$ un grupo finito y
\begin{align*}
G & = G_1 \unrhd G_2 \unrhd \cdots \unrhd G_{s+1} = \{e\}\\
G & = H_1 \unrhd H_2 \unrhd \cdots \unrhd H_{t+1} = \{e\}
\end{align*}
dos series de composición de $G$. Entonces $s = t$ y existe una permutación $\sigma \in S_t$ tal que para toda $i\in\{1,2,\dots ,s\}$
\begin{align*}
G_i/G_{i+1} \cong H_{\sigma(i)}/ H_{\sigma(i)+1}.
\end{align*}

Demostración.

Sea $G$ un grupo finito.
Por inducción sobre $|G|$.

H.I. Supongamos que el resultado se cumple si el orden del grupo es menor que $|G|.$

Sean
\begin{align*}
G & = G_1 \unrhd G_2 \unrhd \cdots \unrhd G_{s+1} = \{e\}\\
G & = H_1 \unrhd H_2 \unrhd \cdots \unrhd H_{t+1} = \{e\}
\end{align*}
dos series de composición de $G$.

Caso 1. $G_2 = H_2$, entonces
\begin{align*}
G_2 \unrhd \cdots \unrhd G_{s+1} = \{e\}\\
H_2 \unrhd \cdots \unrhd H_{t+1} = \{e\}
\end{align*}
son series de composición de $G_2$.

Dado que $G_1/G_2$ es simple, en particular $G_1/G_2\neq \{e_{G_1/G_2}\}$ y así $G=G_1\neq G_2$. En consecuencia $G_2\leq G$ y $|G_2|<|G|$ y por H.I. $s-1 = t-1$ y existe $\sigma\in S_{t-1}$ tal que
\begin{align*}
G_i/ G_{i+1} \cong H_{\sigma(i)} / H_{\sigma(i) + 1} \quad \forall i\in\{2,\dots,t\}.
\end{align*}

Como $G_1 = G = H_1$ y $G_2 = H_2$, entonces $G_1/G_2 = H_1/H_2$.

Así, $s=t$ y $\alpha\in S_t$ con $\alpha(1) = 1$, $\alpha(i) = \sigma(i)$ para $i\in\{2,\dots, t\}$ cumple que
\begin{align*}
G_i/G_{i+1} \cong H_{\alpha(i)} / H_{\alpha(i)+1} \quad \forall i \in \{1,\dots, t\}.
\end{align*}

Caso 2. $G_2 \neq H_2$

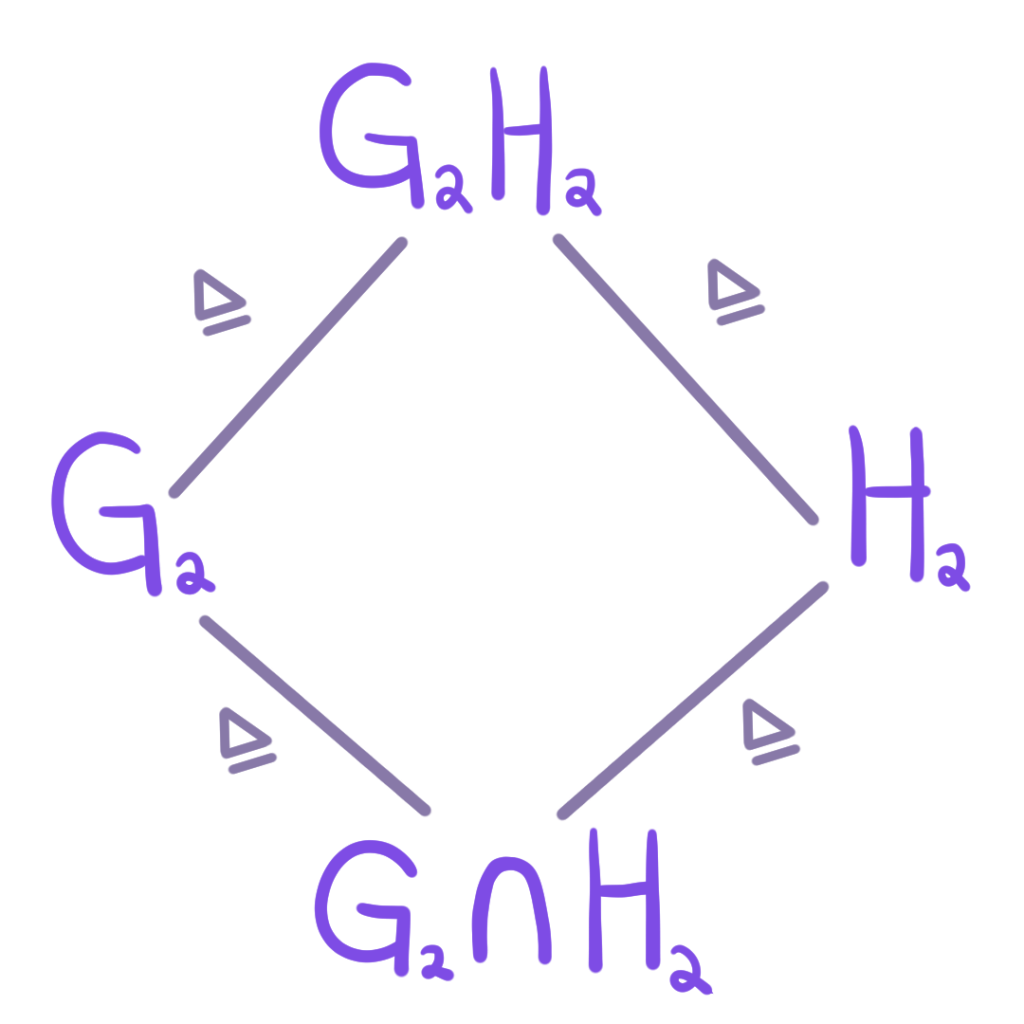
Como $G_2 \unlhd G$ y $H_2 \unlhd G$ se tiene que $G_2H_2 \unlhd G$.

Además
\begin{align*}
G_2 &\leq G_2H_2 \unlhd G \\
H_2 &\leq G_2H_2 \unlhd G.
\end{align*}

Como $G/G_2$ es simple, por el ejercicio 2 de Grupos simples y series de grupos se tiene que $G_2$ es un subgrupo normal de $G$ máximo. Así, $G_2H_2 = G$ ó $G_2H_2 = G_2$. Análogamente $G_2H_2 = G$ ó $G_2H_2 = H_2$. Pero si $G_2H_2 = G_2$ y $G_2H_2 = H_2$ tendríamos que $G_2=H_2$, lo que es una contradicción. Por lo tanto \begin{equation}\label{ec1}G_2H_2 = G.\end{equation}

Como $G_2\unlhd G$ entonces usamos el 2do Teorema de Isomorfía y nos dice que $G_2\cap H_2 \unlhd H_2$ y

\begin{align*}
G_2H_2/G_2 \cong H_2/(G_2\cap H_2).
\end{align*}

Pero, como también $H_2 \unlhd G$, el 2do teorema de isomorfía también nos dice que $G_2 \cap H_2 \unlhd G_2$ y
\begin{align*}
G_2H_2/H_2 \cong G_2/(G_2\cap H_2).
\end{align*}

Por (\ref{ec1}) tenemos que $G = G_2H_2$ obteniendo así que

\begin{align*}
G/G_2 &\cong H_2/(G_2\cap H_2)\\
G/H_2 &\cong G_2/(G_2\cap H_2).
\end{align*}

Como $G/G_2$ es simple, $H_2/(G_2\cap H_2)$ también lo es. Así, $G_2\cap H_2$ es un subgrupo normal máximo de $H_2$.

Análogamente como $G/H_2$ es simple, $G_2/(G_2\cap H_2)$ también lo es. Así, $G_2 \cap H_2$ es un subgrupo normal máximo de $G_2$.

Sea $K_3 = G_2\cap H_2$. Consideremos una serie de composición para $K_3$
\begin{align*}
K_3 \unrhd K_4 \unrhd \cdots \unrhd K_{r+1} = \{e\}.
\end{align*}

Tenemos las siguientes series de composición
\begin{align}
G &= G_1\unrhd G_2 \unrhd \cdots \unrhd G_{s+1} = \{e\} \\
G &= G_1 \unrhd G_2 \unrhd K_3 \unrhd K_4 \unrhd \cdots \unrhd K_{r+1} = \{e\} \\
G &= H_1 \unrhd H_2 \unrhd K_3 \unrhd K_4 \unrhd \cdots \unrhd K_{r+1} = \{e\} \\
G &= H_1 \unrhd H_2 \unrhd \cdots \unrhd H_{t+1} = \{e\}
\end{align}

Por el caso 1 aplicado a $(2)$ y $(3)$, $s= r$ y los factores de composición de
\begin{align*}
G_2 &\unrhd \cdots \unrhd G_{s+1} = \{e\}\\
G_2 &\unrhd K_3 \unrhd K_4 \unrhd \cdots \unrhd K_{r+1} = \{e\}
\end{align*}
son isomorfos salvo por el orden en el que están colocados.

Por el caso 1 aplicado a $(4)$ y $(5)$, $r=t$ y los factores de composición de
\begin{align*}
H_2 &\unrhd K_3 \unrhd K_4 \unrhd \cdots \unrhd K_{r+1} = \{e\}\\
H_2 &\unrhd \cdots \unrhd H_{t+1} = \{e\}
\end{align*}
son isomorfos salvo por el orden en el que están colocados.
Tenemos entonces que $s = t$.

Consideremos $G_i/G_{i+1}$ con $i\in\{2,\dots,t\}$:

Si $G_i/G_{i+1} \cong K_j/K_{j+1}$ con $j\in \{3,\dots, t\}$, entonces sabemos que existe $l\in\{2,\dots, t\}$ tal que $K_j/K_{j+1} \cong H_l/H_{l+1}.$

Por otro lado si $G_i/ G_{i+1} \cong G_2/K_3$, entonces $G_2/K_3=G_2/(G_2\cap H_2) \cong G/H_2=H_1/H_2.$

Entonces, para $i\in\{2,\dots,t\}$ se tiene que $G_i/G_{i+1}$ es isomorfo a $ H_l/H_{l+1}$ para alguna $l\in\{1,2,\dots, t\}$.

Finalmente consideremos el cociente $G/G_2$. Tenemos que $G/G_2\cong H_2/(G_2\cap H_2)=H_2/K_3 \cong H_m/H_{m+1}$, para alguna $m\in \{2,\dots, t\}$.

Por lo tanto para $i\in\{1,2,\dots,t\}$ se tiene que $G_i/G_{i+1}$ es isomorfo a $ H_l/H_{l+1}$ para alguna $l\in\{1,2,\dots, t\}$.

Así, los factores de composición de las series $(1)$ y $(4)$ son isomorfos salvo por el orden en que aparecen.

$\square$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Demuestra que el Teorema de Jordan-Hölder induce el Teorema fundamental de la aritmética.
   1. Toma el grupo cíclico $\z_n$ con $n \in \z$ no necesariamente primo.
   2. Encuentra el orden de un subgrupo máximo de $\z_n$.
   3. Observa la forma de las series de composición de $\z_n$.
   4. Usa el teorema de Jordan-Hölder para concluir el Teorema fundamental de la aritmética.

Más adelante…

Nuestro curso abarca hasta este teorema, pero el estudio del álgebra continúa en un curso de Álgebra Moderna II donde se estudia la Teoría de anillos y la Teoría de Galois. Estas dos teorías son igualmente interesantes y apasionantes y tienen muchas aplicaciones.

Entradas relacionadas

• Ir a Álgebra Moderna I.
• Entrada anterior del curso: Grupos simples y series de grupos.
• Resto de cursos: Cursos.