Introducción
En la entrada anterior vimos que al igual que en $\mathbb{R}^2$, en el plano complejo es posible trabajar con coordenadas polares para representar a un número complejo en su «forma polar», utilizando su módulo y un ángulo. Primeramente definimos al argumento de un número complejo, el cual resultó no ser único, sino que en realidad existe todo un conjunto de ángulos que nos permite representar a un número complejo de manera indistinta, por lo que fue conveniente el considerar a un ángulo en particular, llamado el argumento principal. Considerando la forma polar de un número complejo fue posible dar una interpretación geométrica al producto y división de números complejos. Además obtuvimos algunos resultados importantes, como la fórmula de De Moivre, que nos serán de utilidad a lo largo de esta entrada y en general para poder operar de forma más sencilla a los números complejos.
En esta entrada nuestro objetivo será plantear una ecuación de la forma $w^n = z$, con $n\in\mathbb{N}^+$ y $w,z\in\mathbb{C}$, $z\neq 0$, analizarla y darle solución. Una vez resuelta dicha ecuación, tendrá sentido el pensar en potencias racionales de números complejos.
Raíces de un número complejo.
Definición 5.1. (Raíz $n$-ésima.)
Sea $z \in \mathbb{C}$, con $z\neq0$. Un número complejo $w$ es llamado una raíz $n$-ésima de $z$ si $w^n = z$, y se denota como $w = z^{1/n}$.
Proposición 5.1. (Raíces $n$-ésimas.)
Sea $z\in \mathbb{C}$, $z\neq0$, en su forma polar $z=r\,\text{cis}(\theta)$ y sea $n \in \mathbb{N^+}$. Entonces existen exactamente $n$ raíces $n$-ésimas distintas, las cuales están dadas por:
\begin{equation*}
w_k = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta+2\pi k}{n}\right), \quad \text{para} \quad k = 0,1,\ldots,n-1.
\end{equation*}
Demostración. Dadas las hipótesis, primeramente verifiquemos que el número complejo $w_k$ propuesto cumple la definición 5.1. De acuerdo con la fórmula de De Moivre tenemos que:
\begin{align*}
\left(w_k\right)^n & = \left(\sqrt[n]{r}\right)^n \, \text{cis}\left(n \left[\frac{\theta+2\pi k}{n}\right]\right)\\
& = \left(\sqrt[n]{r}\right)^n \, \text{cis}\left(\theta+2\pi k\right).
\end{align*}
Dado que las funciones seno y coseno son $2\pi$-periódicas, es decir, para todo $k\in\mathbb{Z}$ se cumple:
\begin{equation*}
\operatorname{sen}(\theta + 2\pi k) = \operatorname{sen}(\theta),\quad \operatorname{cos}(\theta + 2\pi k) = \operatorname{cos}(\theta). \end{equation*}
Entonces se tiene que $z = r\,\text{cis}(\theta)= \left(w_k\right)^n$.
Lo anterior nos motiva a encontrar un número complejo $w = \rho \, \text{cis}(\phi)$ tal que $w^n = z$, es decir:
\begin{equation*}
\rho^n \, \text{cis}(n\phi) = r \, \text{cis}(\theta).
\end{equation*}
Considerando la igualdad entre números complejos se tiene que:
\begin{align*}
\rho^n = r,\\
\text{cos}(n\phi) = \text{cos}(\theta),\\
\text{sen}(n\phi) = \text{sen}(\theta).
\end{align*}
Desde que los argumentos de ambos números complejos están determinados módulo $2\pi$, entonces de lo anterior tenemos que:
\begin{equation*}
\rho = \sqrt[n]{r},
\end{equation*}
\begin{equation*}
n\phi = \theta + 2\pi k, \quad \Longrightarrow \quad \phi = \frac{\theta + 2\pi k}{n}, \quad \text{para algún}\, \, k \in \mathbb{Z}.
\end{equation*}
Notemos que para $k=0,1,\ldots,n-1$ se obtienen ya $n$ raíces $n$-ésimas distintas, las cuales tienen el mismo módulo $\sqrt[n]{r}$, pero distinto argumento. Para probar esto consideremos el siguiente:
Lema 5.1. Sean $n\in\mathbb{N^+}$, $k’, k \in \mathbb{Z}$ y sea $w_k = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right)$. Entonces:
\begin{equation*}
k’ \equiv k \,\, (\text{mod}\, n) \quad \text{si y solo si} \quad w_{k’} = w_k.
\end{equation*}
Observación 5.1.
La congruencia módulo $n$, representada por el símbolo $\equiv$, es una relación de equivalencia en $\mathbb{Z}$, la cual se define como sigue:
Para $a,b\in\mathbb{Z}$ y $n\in\mathbb{N}^+$, diremos que $a$ es congruente con $b$ módulo $n$ si y solo si $a-b$ es divisible por $n$ y se escribe como:
\begin{equation*}
a \equiv b \,\, (\text{mod}\, n).
\end{equation*}
Demostración.
$\Rightarrow)$ Dadas las hipótesis, sin pérdida de generalidad tenemos que:
\begin{equation*}
k’ \equiv k \,\, (\text{mod}\, n) \quad \Longrightarrow \quad k’ = k + nm, \, \, \, \text{para algún} \,\, m\in\mathbb{Z} \,\,\, \text{y} \, \, 0\leq k<n.
\end{equation*}
Entonces, considerando que las funciones seno y coseno son $2\pi$-periódicas:
\begin{align*}
w_{k’} & = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k’}{n}\right)\\
& = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi (k +nm) }{n}\right)\\
& = \sqrt[n]{r} \left[ \text{cos}\left(\frac{\theta + 2 \pi (k+nm)}{n}\right) + i\, \text{sen}\left(\frac{\theta + 2\pi (k+nm)}{n}\right) \right]\\
& = \sqrt[n]{r} \left[ \text{cos}\left(\frac{\theta + 2\pi k}{n} + 2\pi m\right) + i\, \text{sen}\left(\frac{\theta + 2\pi k}{n} + 2\pi m\right) \right]\\
& = \sqrt[n]{r} \left[ \text{cos}\left(\frac{\theta + 2\pi k}{n}\right) + i\, \text{sen}\left(\frac{\theta + 2\pi k}{n}\right) \right]\\
& = \sqrt[n]{r}\, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right)\\
& = w_k.
\end{align*}
$(\Leftarrow$ Dadas las hipótesis, tenemos que si $w_k’ = w_k$, entonces:
\begin{equation*}
\sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k’}{n}\right) = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right),
\end{equation*}
por lo que, considerando la igualdad entre números complejos:
\begin{align*}
\text{cos}\left(\frac{\theta + 2\pi k’}{n}\right) = \text{cos}\left(\frac{\theta + 2\pi k}{n}\right),\\
\text{sen}\left(\frac{\theta + 2\pi k’}{n}\right) = \text{sen}\left(\frac{\theta + 2\pi k}{n}\right).
\end{align*}
De donde se sigue que:
\begin{equation*}
\frac{\theta + 2\pi k’}{n} = \frac{\theta + 2\pi k}{n} + 2 \pi m, \quad \text{para algún} \,\, m\in \mathbb{Z}.
\end{equation*}
Por lo que:
\begin{equation*}
k’ = k + nm, \quad \text{para algún} \,\, m\in \mathbb{Z},
\end{equation*}
lo cual implica que $k’ \equiv k \, \, (\text{mod}\,n)$.
$\blacksquare$
De acuerdo con el lema anterior, concluimos que existen a lo más $n$ raíces $n$-ésimas distintas $w_k$ correspondientes a $k = 0, 1, \ldots, n-1$ y que son de la forma:
\begin{equation*}
w_k = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2\pi k}{n}\right).
\end{equation*}
$\blacksquare$
Observación 5.2.
Notemos que la expresión $z^{1/n}$ es $n$-valuada, es decir, no representa un único valor, sino al conjunto de $n$ raíces $n$-ésimas, formado por las raíces $w_k$ con $k=0,1,\ldots,n-1$, del número complejo $z\neq0$.
Definición 5.2. (Raíz $n$-ésima principal.)
Sea $z\neq0$ un número complejo. Llamaremos como raíz $n$-ésima principal de $z$ al único valor de $z^{1/n}$ tal que tenga como argumento al argumento principal de $z$, $\text{Arg}\,z$, es decir a la raíz dada por $k=0$.
Ejemplo 5.1.
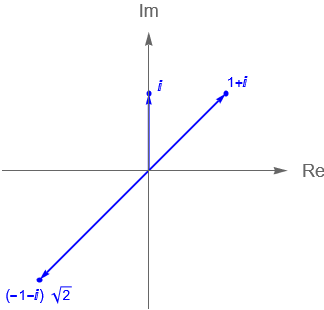
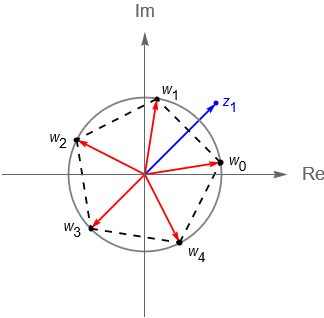
- a) Hallar las 5 raíces quintas de $z_1 = 1+i$.
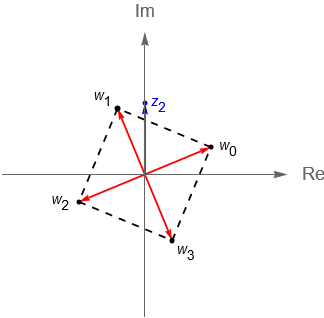
- b) Hallar las 4 raíces cuartas de $z_2 = i$.
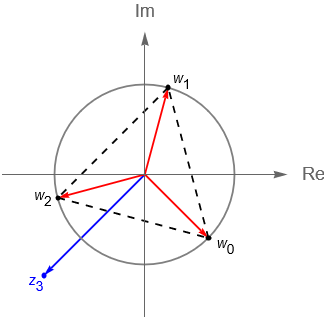
- c) Hallar las 3 raíces quintas de $z_3 = -\sqrt{2} -i\,\sqrt{2}$.
Solución. Para los tres números complejos, resolveremos utilizando su argumento principal $\text{Arg}\,z$.
- a) Notemos que $z_1 = 1+i$ se encuentra en el primer cuadrante, por lo que:
\begin{equation*}
\text{Arg}\,z_1 = \text{arc tan}\left(\frac{1}{1}\right) = \frac{\pi}{4}.
\end{equation*}
Por otra parte, tenemos que $r_1=|\,z_1\,|=\sqrt{2}$. Entonces, por la proposición 5.1 se tiene que las 5 raíces quintas de $z_1$ están dadas por:
\begin{equation*}
w_k = \left(\sqrt{2}\right)^{\frac{1}{5}}\,\text{cis}\left(\frac{\frac{\pi}{4}+2\pi k}{5}\right), \quad \text{para} \, \, k = 0,1,2,3,4.
\end{equation*}
Por lo que:
\begin{equation*}
z^{1/5} = \left\{ \sqrt[10]{2}\,\text{cis}\left(\frac{\pi}{20}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{9\pi}{20}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{17\pi}{20}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{5\pi}{4}\right),\sqrt[10]{2}\,\text{cis}\left(\frac{33\pi}{20}\right)\right\}.
\end{equation*}
De acuerdo con la definición 5.2, $w_0 = \sqrt[10]{2}\,\text{cis}\left(\frac{\pi}{20}\right)$ es la raíz quinta principal de $z_1$.
- b) Sabemos que para $z_2 = i$ se tiene que:
\begin{equation*}
\text{Arg}\,z_2 = \frac{\pi}{2}.
\end{equation*}
Por otra parte, tenemos que $r_2=|\,z_2\,|=1$. Entonces, considerando la proposición 5.1, tenemos que las 4 raíces cuartas de $z_2$ están dadas por:
\begin{equation*}
w_k = 1^{\frac{1}{4}}\,\text{cis}\left(\frac{\frac{\pi}{2}+2\pi k}{4}\right), \quad \text{para} \, \, k = 0,1,2,3.
\end{equation*}
Por lo que:
\begin{equation*}
z^{1/4} = \left\{\text{cis}\left(\frac{\pi}{8}\right),\text{cis}\left(\frac{5\pi}{8}\right),\text{cis}\left(\frac{9\pi}{8}\right),\text{cis}\left(\frac{13\pi}{8}\right)\right\}.
\end{equation*}
Considerando la definición 5.2, se tiene que $w_0 = \text{cis}\left(\frac{\pi}{8}\right)$ es la raíz cuarta principal de $z_2$.
- c) Notemos que $z_3 = -\sqrt{2}-i\,\sqrt{2}$ se encuentra en el tercer cuadrante, por lo que:
\begin{equation*}
\text{Arg}\,z_3 = \text{arc tan}\left(\frac{-\sqrt{2}}{-\sqrt{2}}\right) – \pi= \frac{\pi}{4} – \pi = -\frac{3\pi}{4}.
\end{equation*}
Por otra parte, tenemos que $r_3=|\,z_3\,|=2$. De acuerdo con la proposición 5.1, las 3 raíces cúbicas de $z_3$ están dadas por:
\begin{equation*}
w_k = \sqrt[3]{2}\,\text{cis}\left(\frac{\frac{-3\pi}{4}+2\pi k}{3}\right), \quad \text{para} \, \, k = 0,1,2.
\end{equation*}
Por lo que:
\begin{equation*}
z^{1/3} = \left\{\sqrt[3]{2}\,\text{cis}\left(\frac{-\pi}{4}\right), \sqrt[3]{2}\,\text{cis}\left(\frac{5\pi}{12}\right), \sqrt[3]{2}\,\text{cis}\left(\frac{13\pi}{12}\right)\right\}.
\end{equation*}
De acuerdo con la definición 5.2, se tiene que $w_0 = \sqrt[3]{2}\,\text{cis}\left(\frac{-\pi}{4}\right)$ es la raíz cúbica principal de $z_3$.
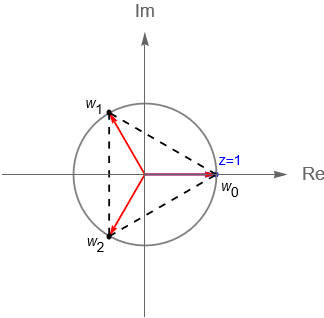
Notemos que las raíces $n$-ésimas tienen una intepretación geométrica, es decir, las raíces $n$-esimas de un número complejo $z$ coinciden con los vértices de un póligono regular de $n$ lados, el cual está inscrito en una circunferencia de radio $\sqrt[n]{r}$ centrada en el origen.
Considerando los números complejos del ejemplo 5.1 tenemos que:
Un caso particular importante es cuando $z=1$. Si se plantea la ecuación $w^n = z$, entonces a las soluciones se les llama las raíces $n$-ésimas de la unidad. Considerando que el argumento principal de $z=1$ es $\text{Arg}\,z = 0$ y $r = |\,z\,| =1$, entonces la forma polar de la unidad es $z=\text{cis}(0)$. De acuerdo con la proposición 5.1 se tiene que las raíces de la unidad están dadas por:
\begin{equation*}
w_k = \sqrt[n]{1}\,\text{cis}\left(\frac{0 + 2 \pi k}{n}\right)= \text{cis}\left(\frac{2 \pi k}{n}\right), \quad \text{para}\, \, k=0,1,\ldots,n-1.
\end{equation*}
Si definimos $\omega = \text{cis}\left(\frac{2 \pi}{n}\right)$, entonces por la fórmula de De Moivre se tiene que $\omega^k$, con $k=0,1,\ldots,n-1 $, determina las $n$ raíces $n$-ésimas de la unidad, es decir:
\begin{equation*}
1, \omega, \omega^2, \omega^3, \ldots, \omega^{n-1}.
\end{equation*}
Ejemplo 5.2.
De acuerdo con lo anterior, tenemos que las 3 raíces cúbicas de la unidad están determinadas por:
\begin{equation*}
\omega = \text{cis}\left(\frac{2\pi}{3}\right) = -\frac{1}{2} + i\,\frac{\sqrt{3}}{2},
\end{equation*}
y son:
\begin{align*}
\omega^0 = 1,\\
\omega = -\frac{1}{2} + i\,\frac{\sqrt{3}}{2},\\
\omega^2 = -\frac{1}{2} – i\,\frac{\sqrt{3}}{2}.
\end{align*}
Observación 5.3.
Es interesante notar que mediante las raíces $n$-ésimas de la unidad es posible encontrar las raíces $n$-ésimas de cualquier $z\in\mathbb{C}$, $z\neq0$, ya que es posible reescribir la fórmula de la proposición 5.1 como sigue:
\begin{align*}
w_k & = \sqrt[n]{r} \, \text{cis}\left(\frac{\theta + 2 \pi k}{n}\right)\\
& = \sqrt[n]{1} \, \text{cis}\left(\frac{2 \pi k}{n}\right) \sqrt[n]{r} \, \text{cis}\left(\frac{\theta}{n}\right)\\
& = \sqrt[n]{r} \, \omega^k \, \zeta,
\end{align*}
donde $\omega = \text{cis}\left(\frac{2 \pi}{n}\right)$, $\zeta = \text{cis}\left(\frac{\theta}{n}\right)$ y $k=0,1,\ldots,n-1$. Entonces para un número complejo $z\neq0$, sus $n$ raíces $n$-ésimas son:
\begin{equation*}
\sqrt[n]{r} \, \zeta, \sqrt[n]{r} \, \omega \, \zeta, \sqrt[n]{r} \, \omega^2 \, \zeta,\ldots, \sqrt[n]{r} \, \omega^{n-1} \, \zeta.
\end{equation*}
Dichas raíces coinciden con los vértices de un polígono de $n$ lados, inscrito en la circunferencia de radio $\sqrt[n]{r}$.
Ejemplo 5.3.
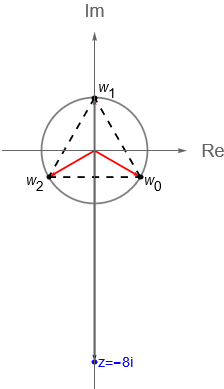
Encontremos las 3 raíces cúbicas de $z=-8i$. Utilizando el argumento principal de $z$, tenemos que $\text{Arg}\,z=-\frac{\pi}{2}$ y $r = |\,z\,| = 8$, por lo que:
\begin{align*}
\sqrt[3]{r} = \sqrt[3]{8} = 2,\ \zeta = \text{cis}\left(\frac{-\frac{\pi}{2}}{3}\right) = \text{cis}\left(\frac{-\pi}{6}\right) = \frac{1}{2}\left(\sqrt{3} – i\right).
\end{align*}
Considerando la observación 5.3, tenemos que las 3 raíces cúbicas de $z=-8i$ están dadas por:
\begin{equation*}
\sqrt[3]{r} \, \zeta, \sqrt[3]{r} \, \omega \, \zeta, \sqrt[3]{r}\, \omega^2 \, \zeta, \end{equation*}
donde $\omega = \text{cis}\left(\frac{2\pi}{3}\right)$ determina las 3 raíces cúbicas de la unidad, como en el ejemplo anterior, entonces:
\begin{align*}
w_0 = 2(1)\left[\frac{1}{2}\left(\sqrt{3} – i\right)\right] = \sqrt{3} – i,\\
w_1 = 2\left(-\frac{1}{2} + i\,\frac{\sqrt{3}}{2}\right)\left[\frac{1}{2}\left(\sqrt{3} – i\right)\right] = 2i,\\
w_2 = 2\left(-\frac{1}{2} – i\,\frac{\sqrt{3}}{2}\right)\left[\frac{1}{2}\left(\sqrt{3} – i\right)\right] = -\sqrt{3} – i.
\end{align*}
Observación 5.4.
Supongamos que $m,n \in \mathbb{N^+}$ son tales que no tienen divisores comunes y sean $z, w \in \mathbb{C}$ con $z=r\,\text{cis}(\theta)\neq0$. Es posible definir las potencias racionales de $z$, es decir $z^{m/n}$. Para entender mejor esta idea pensemos en la ecuación $w^n = z^m$. Entonces es posible mostrar que existen $n$ soluciones distintas para dicha ecuación, las cuales están dadas por las raíces $n$-ésimas de $z^m$ y son de la forma:
\begin{equation*}
w_k = \sqrt[n]{r^m}\,\text{cis}\left(\frac{m(\theta+2 \pi k)}{n}\right), \quad \text{para}\,\, k=0,1,\ldots,n-1.
\end{equation*}
Lo anterior nos dice entonces que los conjuntos $\left(z^m\right)^{1/n}$ y $\left(z^{1/n}\right)^m$ deben ser el mismo, a decir el conjunto $z^{m/n}$.
Tarea moral
- Determina las 3 raíces cúbicas de $z_1=-125$ y las 8 raíces octavas de $z_2=\dfrac{16i}{1+i}$. En ambos casos identifica a la raíz $n$-ésima principal correspondiente y realiza un gráfico de las raíces.
- Considera la observación 5.4 y prueba el resultado. Argumenta porqué los conjuntos de raíces son los mismos.
- Sean $a$ y $b$ dos números reales y $n\in\mathbb{N}^+$. Demuestra que todas las raíces de la ecuación:
\begin{equation*}
\left(\frac{1+iz}{1-iz}\right)^n = a+ib,
\end{equation*}
son reales si y solo si $a^2 + b^2 =1$.
- Resuelve la ecuación $ (z+1)^5 = z^5$.
- Encuentra todas las soluciones de la ecuación $w^2 = (-1+i)^5$.
- Sea $z = \operatorname{cis}\left(\frac{2\pi}{n}\right)$. Prueba que para $n\geq 2$ se cumple:
\begin{equation*}
1+ z + z^2 + \cdots + z^{n-1} = 0.
\end{equation*}
Más adelante…
Como habíamos visto en la entrada anterior, el trabajar con un número complejo en su forma polar nos permitió caracterizar a las potencias enteras de un números complejo en términos de sus módulos y sus argumentos, lo cual fue de utilidad para trabajar con el concepto de raíz $n$-ésima de un número complejo y dar soluciones a ecuaciones de la forma $w^n=z$. Además vimos que es posible caracterizar a dichas soluciones de manera geométrica.
A diferencia de $\mathbb{R}$, notamos que el campo de los números complejos $\mathbb{C}$ es cerrado bajo la radicación, es decir que para todo $z\in\mathbb{C}$ se cumple que el conjunto de números complejos $z^{1/n}$, $n\in\mathbb{N}^+$, sigue siendo un subconjunto de $\mathbb{C}$.
En la siguiente entrada retomaremos el concepto del módulo y sus propiedades con la finalidad de introducir una métrica en $\mathbb{C}$, la cual nos permitirá seguir describiendo desde una perspectiva geométrica a los números complejos y hablar de algunos lugares geométricos del plano complejo.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Forma Polar. Potencias en $\mathbb{C}$.
- Siguiente entrada del curso: Lugares geométricos en $\mathbb{C}$.