Introducción

En la entrada anterior hemos definido formalmente la integral para funciones complejas de variable compleja, que como vimos dicha definición resulta familiar a la de integrales de línea vista en nuestros cursos de Cálculo.

En esta entrada veremos algunos resultados, como el Teorema Fundamental del Cálculo para integrales de contorno y el lema de Goursat, que serán clave al enunciar el Teorema de Cauchy para funciones complejas, que es sin duda un resultado fundamental en la teoría de las funciones analíticas y en general de la teoría de la Variable Compleja.

Definición 35.1. (Primitiva de una función compleja.)
Sean $U\subset\mathbb{C}$ un conjunto abierto y $f:U\to\mathbb{C}$ una función continua en $U$. Se dice que $F:U\to\mathbb{C}$ es una primitiva de $f$ en $U$ si $F$ es una función analítica en $U$ tal que $F'(z)=f(z)$ para todo $z\in U$.

Observación 35.1.
Dado que $f$ es continua y $F$ analítica, en particular continua, entonces por la proposición 19.2 se cumple que cualesquiera dos primitivas de $f$ difieren por una constante compleja.

Para determinar una primitiva de una función compleja continua $f$, podemos recurrir, cuando sea posible, al uso de los resultados de nuestros cursos de Cálculo y verificar mediante las reglas de diferenciación para funciones complejas.

Ejemplo 35.1.
Consideremos a la función $f(z)=ze^z$ y determinemos una primitiva de $f$.

Solución. Es claro que $f$ es una función entera ya que $g(z)=z$ y $h(z)=e^z$ son funciones enteras, proposición 16.2, por lo que en particular es continua en todo $\mathbb{C}$.

Afirmamos que una primitiva de $f$ en $\mathbb{C}$ es $F(z)=ze^z – e^z$. Por la proposición 16.2 tenemos que:
\begin{align*}
F'(z) & =\frac{d}{dz}\left(ze^z – e^z\right)\\
& =\frac{d}{dz}ze^z – \frac{d}{dz}e^z\\
& = e^{z} + ze^z – e^z\\
& = ze^z.
\end{align*}

Ejemplo 35.2.
Determinemos una primitiva de las siguientes funciones complejas.
a) $f(z)=z^3+7z-2$.
b) $f(z)=\operatorname{Log}(z)$.
c) $f(z)=\dfrac{1}{z}$.

Solución. Recurrimos a los resultados de diferenciación para funciones complejas establecidos a lo largo de la segunda unidad del curso.

a) Por el corolario 15.1 es claro que $f$ es una función continua en $\mathbb{C}$ por ser un polinomio complejo.

Una primitiva de $f$ en $\mathbb{C}$ es:
\begin{equation*}
F(z)=\dfrac{z^4}{4} + \dfrac{7z^2}{2} – 2z,
\end{equation*}ya que:
\begin{equation*}
F'(z) =\frac{d}{dz}\left(\dfrac{z^4}{4} + \dfrac{7z^2}{2} – 2z\right) = \frac{1}{4} \frac{d}{dz} z^4 + \dfrac{7}{2}\frac{d}{dz}z^2 – 2\frac{d}{dz}z = z^3+7z-2.
\end{equation*}

b) Por la proposición 21.2 sabemos que $f(z)=\operatorname{Log}(z)$ es una función continua en $D=\mathbb{C}\setminus(-\infty, 0]$.

Una primitiva de $f$ en $D$ es:
\begin{equation*}
F(z)=z\operatorname{Log}(z) – z,
\end{equation*}ya que:
\begin{align*}
F'(z) & = \frac{d}{dz}\left[z\operatorname{Log}(z) – z\right]\\
&= \frac{d}{dz} z\operatorname{Log}(z) -\frac{d}{dz}z\\
& = \operatorname{Log}(z) + z\left(\frac{1}{z}\right) – 1\\
& = \operatorname{Log}(z) + 1 -1\\
& = \operatorname{Log}(z).
\end{align*}

c) Sabemos que $f(z)=\dfrac{1}{z}$ es una función continua en $\mathbb{C}\setminus\{0\}$. En este punto inferimos que una posible primitiva de $f$ está dada por $F(z)=\operatorname{Log}(z)$, sin embargo, de acuerdo con la proposición 21.4, sabemos que la rama principal del logaritmo, dada por la función $F$, únicamente es analítica en $D=\mathbb{C}\setminus(-\infty, 0]$, por lo que si restringimos a $f$ al dominio $D$, en el cual sigue siendo una función continua, entonces es claro que $F$ es una primitiva de $f$ en $D$ ya que:
\begin{equation*}
F'(z) = \frac{d}{dz} \operatorname{Log}(z) = \frac{1}{z} = f(z), \quad \forall z\in D.
\end{equation*}

Proposición 35.1. (Teorema Fundamental del Cálculo para integrales de contorno.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado, $f:U\to\mathbb{C}$ una función continua en $U$ y $\gamma:[a,b]\to U$ un contorno en $U$. Si $F:U\to\mathbb{C}$ es una primitiva de $f$ en $U$, entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = F(\gamma(b)) – F(\gamma(a)).
\end{equation*}

En particular, si $\gamma$ es una contorno cerrado, entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = 0.
\end{equation*}

Demostración. Dadas las hipótesis, consideremos primero el caso en que $\gamma$ es una curva suave. Sean $g, G:[a,b]\to\mathbb{C}$ las funciones híbridas dadas, respectivamente, por:
\begin{equation*}
g(t) = f(\gamma(t))\gamma'(t) \quad \text{y} \quad G(t) = F(\gamma(t)).
\end{equation*}

Dado que $f$ es continua en $U$, $F$ es analítica en $U$ tal que $F'(z)=f(z)$ para todo $z\in U$ y $g$ es de clase $C^1$ en $[a,b]$, entonces $g$ es una función continua en $[a,b]$ y $G$ una función continua en $[a,b]$ y diferenciable en $(a,b)$. Por la regla de la cadena, proposición 32.2, tenemos que:
\begin{align*}
\frac{d}{dt} G(t) & = F'(\gamma(t))\gamma'(t)\\
&= f(\gamma(t))\gamma'(t)\\
& = g(t), \quad \forall t\in(a,b),
\end{align*}es decir, $G$ es una primitiva de $g$, definición 33.2.

Por lo tanto, del segundo TFC para funciones híbridas, proposición 33.2, se tiene que:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{a}^{b} f(\gamma(t))\gamma'(t) dt\\
& = \left. G(t)\right|_{a}^{b}\\
& = \left. F(\gamma(t))\right|_{a}^{b}\\
& = F(\gamma(b)) – F(\gamma(a)).
\end{align*}

Si $\gamma$ es de clase $C^1$ a trozos, entonces por definición podemos elegir a la partición:
\begin{equation*}
P : a=t_0 < t_1 < \cdots < t_{n-1}<t_n=b,
\end{equation*}del intervalo $[a,b]$, tal que $\gamma_k=\left.\gamma\right|_{[t_{k-1}, t_k]}$ es una curva suave para $1\leq k\leq n$, entonces:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{\gamma_1} f(z) dz + \cdots + \int_{\gamma_n} f(z) dz\\
& = F(\gamma(t_1)) – F(\gamma(a)) + F(\gamma(t_2)) – F(\gamma(t_1)) + \cdots + F(\gamma(b)) – F(\gamma(t_{n-1}))\\
& = F(\gamma(b)) – F(\gamma(a)).
\end{align*}

Por último, si el contorno $\gamma$ es cerrado, entonces $\gamma(a) = \gamma(b)$, en tal caso, de lo anterior se sigue que:
\begin{equation*}
\int_{\gamma} f(z) dz = F(\gamma(b)) – F(\gamma(a)) = 0.
\end{equation*}

$\blacksquare$

Observación 35.2.
El resultado anterior es de suma importancia, ya que establece que para cualquier contorno $\gamma$ en un conjunto abierto $U\subset\mathbb{C}$, si $f:U\to\mathbb{C}$ es una función continua con primitiva $F$ en $U$, entonces la integral de contorno de $f$ no depende de $\gamma$, sino únicamente de sus extremos.

Ejemplo 35.3.
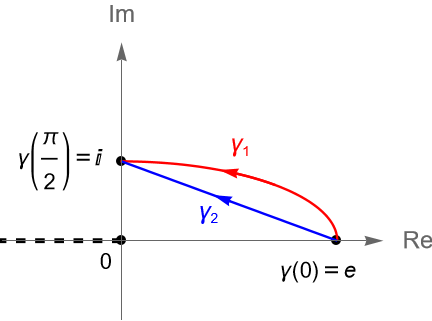
Evaluemos la integral $\int_{\gamma} z^{-1} dz$ a lo largo de los contornos:
\begin{align*}
\gamma_1(t)&=e\operatorname{cos}(t)+i\operatorname{sen}(t), \quad \forall \, t\in[0,\pi/2],\\
\gamma_2(t) &= e(1-t)+it, \quad \forall \, t\in[0,1].
\end{align*}

Solución. Sean $f(z)=z^{-1}$ y $F(z)=\operatorname{Log}(z)$. Sabemos que $f$ es una función analítica en $\mathbb{C}\setminus\{0\}$ mientras que $F$ es una función analítica en $D=\mathbb{C}\setminus(-\infty, 0]$, por lo que si restringimos a $f$ al dominio $D$, entonces:
\begin{equation*}
F'(z) = \frac{d}{dz} \operatorname{Log}(z) = \dfrac{1}{z} = f(z), \quad \forall z\in D,
\end{equation*}es decir, $F$ es una primitiva de $f$ en $D$.

Claramente $\gamma_1$ y $\gamma_2$ son dos contorno en $D$, figura 127, tales que $\gamma_1(0)=\gamma_2(0)=e$ y $\gamma_1(\pi/2)=\gamma_1(\pi/2)=i$. Entonces, de la proposición 35.1 se sigue que:
\begin{equation*}
\int_{\gamma_1} z^{-1} dz = \left. F(\gamma_1(t))\right|_{0}^{\pi/2} = \operatorname{Log}(i) – \operatorname{Log}(e) = -1 + i\frac{\pi}{2}.
\end{equation*}
\begin{equation*}
\int_{\gamma_2} z^{-1} dz = \left. F(\gamma_2(t))\right|_{0}^{\pi/2} = \operatorname{Log}(i) – \operatorname{Log}(e) = -1 + i\frac{\pi}{2}.
\end{equation*}

Ejemplo 35.4.
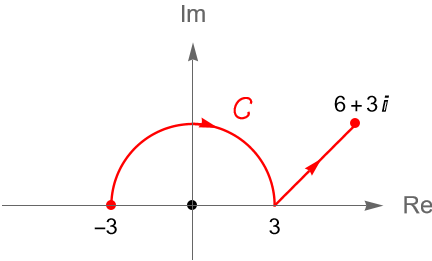
Evaluemos la integral $\int_{C} \operatorname{sen}(z) dz$, donde $C$ es el contorno dado en la figura 128.

Solución. Dado que $f(z)=\operatorname{sen}(z)$ es una función entera y $F(z)=-\operatorname{cos}(z)$ es una primitiva de $f$ en $\mathbb{C}$, entonces por la proposición 35.1 tenemos que:
\begin{equation*}
\int_{C} \operatorname{sen}(z) dz = \left. -\operatorname{cos}(z)\right|_{-3}^{6+3i} = -\operatorname{cos}(6+3i) + \operatorname{cos}(-3).
\end{equation*}

Corolario 35.1. (Integración por partes para integrales de contorno.)
Sean $D\subset\mathbb{C}$ un dominio, $[a,b]\subset\mathbb{R}$, con $a<b$ y $f, g: D \to\mathbb{C}$ dos funciones analíticas en $D$. Entonces, para cualquier contorno $\gamma:[a,b]\to D$ en $D$ se cumple que:
\begin{equation*}
\int_{\gamma} f(z) g'(z) dz = \left. f(z) g(z)\right|_{a}^{b} – \int_{\gamma} f'(z) g(z) dz.
\end{equation*}

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Ejemplo 35.5.
Si $f(z)=z$ y $g(z)=-\operatorname{cos}(z)$ y $\gamma$ describe al contorno $C$ en la figura 128, entonces por el corolario 35.1 tenemos que:
\begin{align*}
\int_{C} z \operatorname{sen}(z) dz & = \left.-z\operatorname{cos}(z)\right|_{-3}^{6+3i} + \int_{C} \operatorname{cos}(z) dz\\
& = -(6+3i)\operatorname{cos}(6+3i) -3\operatorname{cos}(-3) +\left.\operatorname{sen}(z)\right|_{-3}^{6+3i}\\
& = -(6+3i)\operatorname{cos}(6+3i) -3\operatorname{cos}(-3) + \operatorname{sen}(6+3i) – \operatorname{sen}(-3).
\end{align*}

Proposición 35.2.
Sean $D\subset\mathbb{C}$ un dominio, $[a,b]\subset\mathbb{R}$, con $a<b$, un intervalo cerrado, $f:D\to\mathbb{C}$ una función continua en $D$ y $\gamma:[a,b]\to D$ un contorno en $D$. Las siguientes condiciones son equivalentes.

1. Existe una primitiva de $f$ en $D$.
2. Si el contorno $\gamma$ es cerrado, entonces:
   \begin{equation*}
   \int_{\gamma} f(z) dz = 0.
   \end{equation*}
3. Las integrales de contorno de $f$ son independientes del contorno en $D$, es decir, si $\gamma_1$ y $\gamma_2$ son cualesquiera dos contornos en $D$ tales que tienen los mismos puntos inicial y final, entonces:
   \begin{equation*}
   \int_{\gamma_1} f(z) dz = \int_{\gamma_2} f(z) dz.
   \end{equation*}

Demostración. Dadas las hipótesis, del teorema 35.1 se sigue que $1\Rightarrow 2$ y $1\Rightarrow 3$. Veamos que $2\Rightarrow 3$ y $3\Rightarrow 1$.

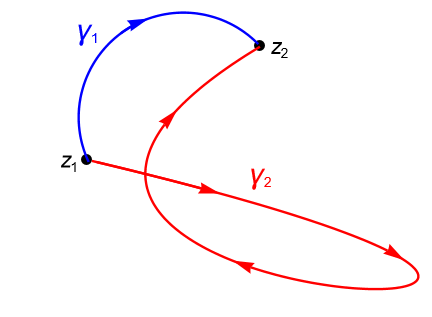
Supongamos que se cumple $2$. Sean $z_1, z_2 \in D$ dos puntos fijos. Si $\gamma_1$ y $\gamma_2$ son dos contornos en $D$ tales que ambos unen a $z_1$ con $z_2$, como en la figura 129, definimos al contorno cerrado $\gamma=\gamma_1+(-\gamma_2)$, entonces, por la proposición 34.2, tenemos que:
\begin{align*}
0 = \int_{\gamma} f(z) dz & = \int_{\gamma_1} f(z) dz + \int_{-\gamma_2} f(z) dz\\
& = \int_{\gamma_1} f(z) dz – \int_{\gamma_2} f(z) dz,
\end{align*}por lo que:
\begin{equation*}
\int_{\gamma_1} f(z) dz = \int_{\gamma_2} f(z) dz.
\end{equation*}Entonces $2\Rightarrow 3$.

Supongamos que se cumple $3$. Sea $z_0\in D$ un punto fijo y para cualquier $z_1\in D$ consideramos al contorno $\gamma$ que une a $z_0$ con $z_1$. Definimos:
\begin{equation*}
F(z_1) := \int_{\gamma} f(z) dz.
\end{equation*}

Dado que $D$ es un dominio, es decir, es un conjunto abierto y conexo, del teorema 10.1 se sigue que $D$ es poligonal conexo, por lo que al menos existe un contorno poligonal en $D$ que une a $z_0$ y $z_1$. Como se cumple la condición $3$, entonces no importa el contorno que elijamos, ya que todos los posibles contornos en $D$ nos darán el mismo valor para $F(z_1)$. Por lo tanto, $F(z_1)$ es una función compleja bien definida en $D$.

Como $D$ es abierto, para algún $\varepsilon_1>0$, si $h\in\mathbb{C}$ es tal que $|h|<\varepsilon_1$, entonces el segmento de recta que va de $z_1$ a $z_1+h$, es decir, $[z_1, z_1+h]$, está completamente contenido en $D$ y se puede parametrizar como $\beta(t)=z_1+ht$, para $t\in[0,1]$.

Tenemos que:
\begin{equation*}
F(z_1+h)=\int_{\gamma+\beta} f(z)dz = \int_{\gamma} f(z)dz + \int_{\beta} f(z)dz,
\end{equation*}por lo que:
\begin{align*}
F(z_1+h) – F(z_1) & = \int_{\gamma} f(z)dz + \int_{\beta} f(z)dz – \int_{\gamma} f(z)dz\\
& = \int_{\beta} f(z)dz,
\end{align*}entonces:
\begin{equation*}
\frac{F(z_1+h) – F(z_1)}{h} = \frac{1}{h} \int_{\beta} f(z)dz.
\end{equation*}

Por otra parte:
\begin{equation*}
\ell(\beta) = \int_{0}^{1} |\beta'(t)|dt = \int_{0}^{1} |h|dt = |h|.
\end{equation*}

Es claro que $f(z_1)$ y $h$ son constantes, por lo que:
\begin{align*}
\int_{\beta} \frac{f(z_1)}{h} dz & = \frac{f(z_1)}{h} \int_{\beta} dz\\
& = \frac{f(z_1)}{h} \int_{0}^{1} \gamma'(t) dt\\
& = \frac{f(z_1)}{h} \int_{0}^{1} h dt\\
& = f(z_1).
\end{align*}

Considerando lo anterior tenemos que:
\begin{equation*}
\frac{F(z_1+h) – F(z_1)}{h} – f(z_1) = \int_{\beta} \frac{f(z) – f(z_1)}{h} dz.
\end{equation*}

Como $f$ es una función continua en $D$, en particular lo es en $z_1$, entonces dado $\varepsilon>0$ existe $\delta>0$ tal que:
\begin{equation*}
|z-z_1|<\delta \quad \Longrightarrow \quad |f(z)-f(z_1)| < \varepsilon.
\end{equation*}

Por lo que, si $|h|<\delta$, entonces para todo $z\neq z_1$ en el segmento de recta $[z_1, z_1+h]$, se cumple que $|z-z_1|\leq |h| < \delta$. Por lo tanto, si $|h|<\delta$, entonces, por la proposición 34.3(5), se tiene que:
\begin{align*}
\left| \frac{F(z_1+h) – F(z_1)}{h} – f(z_1)\right| & = \left|\int_{\beta} \frac{f(z) – f(z_1)}{h} dz.\right|\\
& \leq \int_{\beta} \left|\frac{f(z) – f(z_1)}{h}\right| |dz|\\
& < \int_\beta \frac{\varepsilon}{|h|} |dz|\\
& = \frac{\varepsilon}{|h|} \int_\beta |dz|\\
& = \frac{\varepsilon}{|h|} \ell(\beta)\\
& =\varepsilon,
\end{align*}es decir, si $|h|<\delta$ se cumple que:
\begin{equation*}
\left| \frac{F(z_1+h) – F(z_1)}{h} – f(z_1)\right| < \varepsilon.
\end{equation*}

Como $\varepsilon>0$ es arbitrario, entonces:
\begin{equation*}
\lim\limits_{h\to 0} \frac{F(z_1+h) – F(z_1)}{h} = f(z_1).
\end{equation*}

Dado que $z_1\in D$ es arbitrario, entonces $F'(z_1) = f(z_1)$ para todo $z_1\in D$, es decir, existe una primitiva de $f$ en $D$.

$\blacksquare$

Ejemplo 35.6.
Sean $z_0\in\mathbb{C}$ fijo, $n\in\mathbb{Z}$ y $D = \overline{B}(0,1)$, es decir, el disco cerrado unitario. Veamos que:
a) $f(z)=\dfrac{1}{z}$ no tiene primitiva en $D$;
b) $g(z)=(z-z_0)^n$ tiene primitiva en $D$ si $n\neq -1$.

Solución. Es claro que el contorno cerrado descrito por $\gamma(t)=e^{it}$, con $t\in[0,2\pi]$, es decir, la circunferencia unitaria $C(0,1)$, es un contorno en $\overline{B}(0,1)$.

a) De acuerdo con el ejemplo 34.1 se tiene que:
\begin{equation*}
\int_{\gamma} \frac{1}{z} dz = i2\pi \neq 0,
\end{equation*}entonces, por la proposición 35.3 concluimos que no existe una primitiva de $f$ en $D$.

b) De acuerdo con el ejemplo 34.2 tenemos que:
\begin{equation*}
\int_{\gamma} (z-z_0)^n dz = \left\{ \begin{array}{lcc}
0 & \text{si} & n \neq -1, \\ \\
i2\pi & \text{si} & n=-1,
\end{array} \right.
\end{equation*}por lo que de la proposición 35.3 se sigue que $g(z)=(z-z_0)^n$ tiene primitiva en $D$, dada por:
\begin{equation*}
G(z) = \dfrac{(z-z_0)^{n+1}}{n+1},
\end{equation*}si $n\in\mathbb{Z}$ y $n\neq 1$.

Ejemplo 35.7.
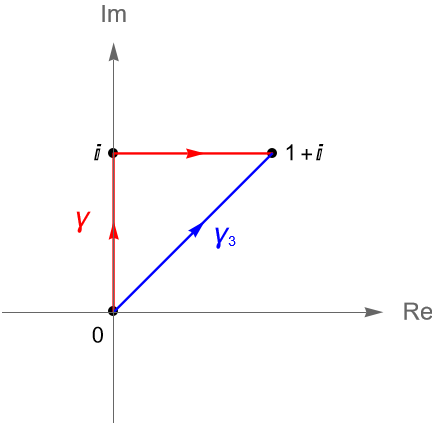
Sean $z=x+iy\in\mathbb{C}$, $f(z)=(y-x)+i3x^2$ y $\gamma=\gamma_1+\gamma_2$, donde $\gamma_1(t)=it$ y $\gamma_2(t)=t+i$, con $t\in[0,1]$, figura 130.

Veamos que $f$ no tiene primitiva en $\mathbb{C}$.

Solución. Es claro que $f$ es una función continua en $\mathbb{C}$ y que $\gamma$ es un contorno en $\mathbb{C}$.

De acuerdo con las proposiciones 33.2 y 34.2 tenemos que:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz\\
& = \int_{0}^{1} f(\gamma_1(t))\gamma’_1(t) dt + \int_{0}^{1} f(\gamma_2(t))\gamma’_2(t) dt\\
& = \int_{0}^{1} it dt + \int_{0}^{1} (1-t+i3t^2) dt\\
& = \left.\frac{it^2}{2}\right|_{0}^{1} + \left.\left(t-\frac{t^2}{2}+it^3\right)\right|_{0}^{1}\\
& = \frac{i}{2} + \frac{1}{2} + i\\
& = \frac{1}{2} + \frac{3}{2} i.
\end{align*}

Si consideramos al contorno $\gamma_3(t)=t+it$, con $t\in[0,1]$, no es difícil verificar que $\gamma$ y $\gamma_3$ tienen los mismos puntos inicial y final, pero:
\begin{align*}
\int_{\gamma_3} f(z) dz & = \int_{0}^{1} f(\gamma_3(t))\gamma’_3(t) dt\\
& = \int_{0}^{1} 3i(1+i)t^3 dt\\
& = \left. i(1+i)t^3\right|_{0}^{1}\\
& = -1 + i,
\end{align*}es decir:
\begin{equation*}
\int_{\gamma} f(z) dz \neq \int_{\gamma_3} f(z) dz,
\end{equation*}entonces, por la proposición 35.2 concluimos que $f$ no tiene primitiva en $\mathbb{C}$.

Ejemplo 35.8.
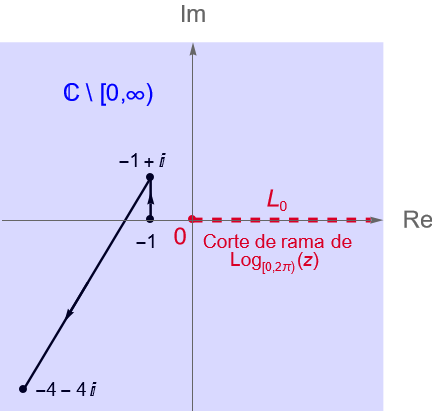
Sean $z_1=-1, z_2=-1+i, z_3=-4-4i\in\mathbb{C}$. Evaluemos la integral:
\begin{equation*}
\int_{[z_1,z_2,z_3]} \frac{1}{z} dz.
\end{equation*}

Solución. De acuerdo con la figura 131 es claro que el contorno poligonal $[z_1, z_2, z_3]$ pasa por la rama de corte de la rama principal del logaritmo, por tal motivo no podemos utilizar a dicha función como primitiva de $f(z)=z^{-1}$. Sin embargo, si consideramos a la rama natural del logaritmo, definición 21.3, es decir:
\begin{equation*}
F(z)=\operatorname{Log}_{[0,2\pi)}(z) = \operatorname{ln}|z| + i \operatorname{Arg}_{[0,2\pi)}(z),
\end{equation*}tenemos que dicha rama tiene como corte de rama al semieje real positivo, incluyendo el origen, y que dicha rama es analítica en $D = \mathbb{C}\setminus{[0,\infty)}$, por lo que podemos considerar dicho dominio para la función $f$, pues ahí es una función continua.

Por la proposición 21.5 tenemos que:
\begin{equation*}
F'(z) = \frac{d}{dz} \operatorname{Log}_{[0,2\pi)}(z) = \frac{1}{z} = f(z), \quad \forall z \in D.
\end{equation*}

Entonces, de la proposición 35.2 se sigue que:
\begin{align*}
\int_{[z_1,z_2,z_3]} \frac{1}{z} dz & = F(z_3) – F(z_1)\\
& = \operatorname{ln}|-4-4i| + i \operatorname{Arg}_{[0,2\pi)}(-4-4i) – \operatorname{ln}|-1| – i \operatorname{Arg}_{[0,2\pi)}(-1)\\
& = \operatorname{ln} \left(4\sqrt{2}\right) + i\frac{5\pi}{4} – \operatorname{ln}(1) – i\pi\\
& = \operatorname{ln} \left(4\sqrt{2}\right) + i\frac{5\pi}{4}\operatorname{Arg}_{[0,2\pi)}(-4-4i) – \operatorname{ln}(1) – i\pi\\
& = \frac{5}{2}\operatorname{ln}(2) + i\frac{\pi}{4}.
\end{align*}

Observación 35.3.
Hasta ahora hemos visto que muchas funciones complejas tienen primitivas. Por ejemplo, del corolario 16.1 se sigue que cualquier polinomio complejo:
\begin{equation*}
p(z)=c_0 + c_1 z + \cdots + c_n z^n,
\end{equation*}tiene como primitiva al polinomio:
\begin{equation*}
P(z)=c_0z + \frac{c_1}{2} z^2 + \cdots + \frac{c_n}{n+1} z^{n+1}.
\end{equation*}

Motivados en lo anterior y considerando los resultados de la tercera unidad podemos establecer la siguiente:

Proposición 35.3.
Sean $z_0\in\mathbb{C}$ fijo y $f:B(z_0, R)\to\mathbb{C}$ una función dada por la serie de potencias:
\begin{equation*}
f(z) = \displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n
\end{equation*}con radio de convergencia $R>0$. Entonces:
\begin{equation*}
F(z) = \sum_{n=0}^\infty \frac{c_n}{n+1} (z-z_0)^{n+1},
\end{equation*}tiene el mismo radio de convergencia $R>0$ y $F'(z)=f(z)$ para todo $z\in B(z_0, R)$.

Demostración. Dadas las hipótesis, es suficiente probar que $F(z)$ tiene el mismo radio de convergencia que $f(z)$, ya que por la proposición 30.2 podemos diferenciar término a término a la serie que define a $F$ y así obtener el resultado.

Por la corolario 29.3 tenemos que:
\begin{equation*}
R = \lim\limits_{n\to\infty} \left|\frac{c_{n}}{c_{n+1}}\right| = \lim\limits_{n\to\infty} \left|\frac{c_{n-1}}{c_n}\right|.
\end{equation*}

Notemos que:
\begin{equation*}
\sum_{n=0}^\infty \frac{c_n}{n+1} (z-z_0)^{n+1} = \sum_{n=1}^\infty \frac{c_{n-1}}{n} (z-z_0)^{n} : = \sum_{n=1}^\infty b_n (z-z_0)^{n},
\end{equation*}donde $b_n = \dfrac{c_{n-1}}{n}$.

Si $R’$ es el radio de convergencia de $F(z)$, entonces:
\begin{align*}
R’ & = \lim\limits_{n\to\infty} \left|\frac{b_{n}}{b_{n+1}}\right|\\
& = \lim\limits_{n\to\infty} \left|\dfrac{c_{n-1}}{n} \dfrac{n+1}{c_{n}}\right|\\
& = \lim\limits_{n\to\infty} \left|\dfrac{c_{n-1}}{c_n}\right| \left|\dfrac{n+1}{n}\right|\\
& = \lim\limits_{n\to\infty} \left|\dfrac{c_{n-1}}{c_n}\right| \lim\limits_{n\to\infty} \left|1+\dfrac{1}{n}\right|\\
& = R.
\end{align*}

$\blacksquare$

Observación 35.4.
Si $f(z)=\displaystyle \sum_{n=0}^\infty c_n (z-z_0)^n$ tiene disco de convergencia $B(z_0, R)$, entonces para cualquier contorno $\gamma$ en $B(z_0, R)$, que une a los puntos $z_1, z_2 \in B(z_0, R)$, se tiene que:
\begin{equation*}
\int_{\gamma} f(z) dz = \sum_{n=0}^\infty \frac{c_n}{n+1} (z_2-z_0)^{n+1} – \sum_{n=0}^\infty \frac{c_n}{n+1} (z_1-z_0)^{n+1}.
\end{equation*}

En particular, para cualquier contorno $\gamma$ en $B(z_0, R)$ que une a $z_0$ con $z\in B(z_0, R)$ se tiene que:
\begin{equation*}
\int_{\gamma} f(z) dz = \sum_{n=0}^\infty \frac{c_n}{n+1} (z-z_0)^{n+1}.
\end{equation*}

Ejemplo 35.9.
Evaluemos la integral:
\begin{equation*}
\int_{C(0,1)} \frac{\operatorname{cos}^2(z)}{z^3} dz.
\end{equation*}

Solución. De acuerdo con el ejemplo 31.1 tenemos que:
\begin{align*}
\operatorname{cos}^2(z) & = \frac{1}{2} + \sum_{n=0}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n}}{(2n)!}\\
& = 1 + \sum_{n=1}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n}}{(2n)!}.
\end{align*}

Dado que la serie del coseno tiene radio de convergencia infinito, entonces la serie del lado derecho de la igualdad también tiene radio de convergencia infinito, entonces:
\begin{align*}
\frac{\operatorname{cos}^2(z)}{z^3} & = \frac{1}{z^3} \left( 1 + \sum_{n=1}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n}}{(2n)!}\right)\\
& = z^{-3} -z^{-1} + \sum_{n=2}^\infty \frac{i^{2n} \, 2^{2n-1} \, z^{2n-3}}{(2n)!}\\
& = z^{-3} -z^{-1} + \sum_{k=0}^\infty c_k z^{k},
\end{align*}donde:
\begin{equation*}
c_k = \left\{ \begin{array}{lc}
\dfrac{i^{2n} \, 2^{2n-1}}{(2n)!} & \text{si existe} \,\, n\in\mathbb{N} \,\, \text{tal que} \,\, k=2n-3,\\
\\ 0 & \text{en otro caso.}
\end{array}
\right.
\end{equation*}

Por lo que:
\begin{equation*}
\frac{\operatorname{cos}^2(z)}{z^3} = z^{-3} -z^{-1} + F(z),
\end{equation*}donde $F(z) = \displaystyle \sum_{k=0}^\infty \dfrac{c_k}{k+1} z^{k}$, entonces, por el ejemplo 35.6(b) y la proposición 35.3, tenemos que:
\begin{align*}
\int_{C(0,1)} \frac{\operatorname{cos}^2(z)}{z^3} dz & = \int_{C(0,1)} \left[ z^{-3} -z^{-1} + F(z)\right] dz\\
& = \int_{C(0,1)} z^{-3} dz – \int_{C(0,1)} z^{-1} dz + \int_{C(0,1)} F(z) dz\\
& = 0 – i2\pi + 0\\
& = – i2\pi.
\end{align*}

Cerraremos esta entrada con un resultado que nos será de mucha utilidad la siguiente entrada al probar el teorema de Cauchy.

Lema 35.1. (Lema de Goursat.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $R\subset U$ un rectángulo cerrado y $f:U\to\mathbb{C}$ una función analítica en $U$. Entonces:
\begin{equation*}
\int_{\partial R} f(z) dz = 0.
\end{equation*}

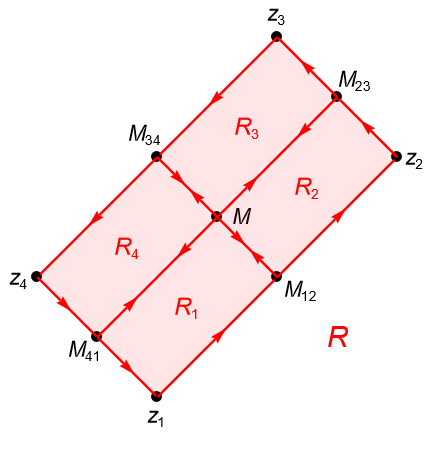
Demostración. Dadas las hipótesis, procedemos a subdividir al rectángulo $R$, con vértices $z_1,z_2,z_3,z_4\in U$, en cuatro subrectángulos congruentes denotados por $R_1, R_2, R_3$ y $R_4$. Si orientamos positivamente a las fronteras de los cuatro subrectángulos, figura 132, por la proposición 34.2(3) tenemos que:
\begin{align*}
\int_{\partial R_1} f(z) dz & = \int_{z_1}^{M_{12}} f(z) dz + \int_{M_{12}}^{M} f(z) dz + \int_{M}^{M_{41}} f(z) dz + \int_{M_{41}}^{z_1} f(z) dz,\\
\int_{\partial R_2} f(z) dz & =\int_{M_{12}}^{z_2} f(z) dz + \int_{z_2}^{M_{23}} f(z) dz + \int_{M_{23}}^{M} f(z) dz + \int_{M}^{M_{12}} f(z) dz,\\
\int_{\partial R_3} f(z) dz & =\int_{M}^{M_{23}} f(z) dz + \int_{M_{23}}^{z_3} f(z) dz + \int_{z_3}^{M_{34}} f(z) dz + \int_{M_{34}}^{M} f(z) dz,\\
\int_{\partial R_4} f(z) dz & =\int_{M_{41}}^{M} f(z) dz + \int_{M}^{M_{34}} f(z) dz + \int_{M_{34}}^{z_{4}} f(z) dz + \int_{z_{4}}^{M_{41}} f(z) dz.
\end{align*}

De acuerdo con lo anterior y la proposición 34.2(2), es claro que:
\begin{align*}
\int_{\partial R} f(z) dz & = \int_{z_1}^{z_2} f(z) dz + \int_{z_2}^{z_3} f(z) dz + \int_{z_3}^{z_{4}} f(z) dz + \int_{z_{4}}^{z_1} f(z) dz,\\
& = \int_{z_1}^{M_{12}} f(z) dz + \int_{M_{12}}^{z_2} f(z) dz + \int_{z_2}^{M_{23}} f(z) dz + \int_{M_{23}}^{z_3} f(z) dz\\
& \quad \quad + \int_{z_{3}}^{M_{34}} f(z) dz + \int_{M_{34}}^{z_{4}} f(z) dz + \int_{z_{4}}^{M_{41}} f(z) dz + \int_{M_{41}}^{z_{1}} f(z) dz,\\
& = \int_{\partial R_1} f(z) dz + \int_{\partial R_2} f(z) dz + \int_{\partial R_3} f(z) dz + \int_{\partial R_4} f(z) dz.
\end{align*}

De la desigualdad del triángulo se sigue que:
\begin{equation*}
\left |\int_{\partial R} f(z) dz \right| \leq \left |\int_{\partial R_1} f(z) dz \right| + \left |\int_{\partial R_2} f(z) dz \right| + \left |\int_{\partial R_3} f(z) dz \right| + \left |\int_{\partial R_4} f(z) dz \right|.
\end{equation*}

Notemos que si cada término en la suma anterior es tal que:
\begin{equation*}
\left |\int_{\partial R_j} f(z) dz \right| < \frac{1}{4}\left |\int_{\partial R} f(z) dz \right|,
\end{equation*}con $j=1,2,3,4$, entonces obtenemos que:
\begin{equation*}
\left |\int_{\partial R} f(z) dz \right| = \left |\sum_{j=1}^{4} \int_{\partial R_{i}} f(z) dz \right| \leq \sum_{j=1}^{4} \left | \int_{\partial R_{i}} f(z) dz \right| < \left |\int_{\partial R} f(z) dz \right|,
\end{equation*}lo cual es una contradicción. Por lo que, existe $k\in\{1,2,3,4\}$ tal que:
\begin{equation*}
\left |\int_{\partial R_k} f(z) dz \right| \geq \frac{1}{4}\left |\int_{\partial R} f(z) dz \right|.
\end{equation*}

Sin pérdida de generalidad denotemos a dicho rectángulo $R_k$ como $R^{(1)}$, es decir, sea $R^{(1)} := R_k$. En caso de existir más de un rectángulo con la propiedad anterior, basta con tomar a $R^{(1)}$ como el rectángulo $R_j$, $j=1,2,3,4$, tal que:
\begin{equation*}
\left |\int_{\partial R^{(1)}} f(z) dz \right| = \max\limits_{1\leq j \leq 4} \left |\int_{\partial R_{j}} f(z) dz \right|.
\end{equation*}

De manera análoga podemos aplicar la misma subdivisión al rectángulo $R^{(1)}$ para obtener un rectángulo $R^{(2)}$ tal que:
\begin{equation*}
\left |\int_{\partial R^{(2)}} f(z) dz \right| \geq \frac{1}{4}\left |\int_{\partial R^{(1)}} f(z) dz \right| \geq \frac{1}{4^2}\left |\int_{\partial R} f(z) dz \right|.
\end{equation*}

Procediendo de manera inductiva con esta subdivisión, podemos construir la sucesión de rectángulos cerrados anidados $\{R^{(n)}\}_{n\geq 1}$, en $U$, es decir:
\begin{equation*}
U \supset R \supset R^{(1)} \supset R^{(2)} \supset R^{(3)} \supset \cdots,
\end{equation*}tal que:
\begin{equation*}
\left |\int_{\partial R^{(n)}} f(z) dz \right| \geq \frac{1}{4} \left |\int_{\partial R^{(n-1)}} f(z) dz \right| \geq \cdots \geq \frac{1}{4^n} \left |\int_{\partial R} f(z) dz \right|,
\end{equation*}es decir:
\begin{equation*}
\left |\int_{\partial R} f(z) dz \right| \leq 4^n \left |\int_{\partial R^{(n)}} f(z) dz \right|, \quad \forall n\in\mathbb{N}^+. \tag{35.1}
\end{equation*}

Denotamos a $d$ como la longitud de una diagonal del rectángulo $R$ y a $L$ como su perímetro. En consecuencia, para todo $n\in\mathbb{N}^+$, $d_n$ es la longitud de una diagonal del rectángulo $R^{(n)}$ y $L_n$ su perímetro. Entonces, por construcción:
\begin{equation*}
d_n = \frac{d}{2^{n}} \quad \text{y} \quad L_n = \frac{L}{2^{n}}, \quad \forall n\in\mathbb{N}^{+}. \tag{35.2}
\end{equation*}

Como la sucesión $\left\{R^{(n)}\right\}_{n\geq 1}$ de rectángulos anidados, está formada por conjuntos cerrados y acotados en $U$, entonces por el Teorema de Cantor, proposición 10.11, tenemos que existe $z_0 \in \bigcap\limits_{n=1}^\infty R^{(n)}$, por lo que $z_0\in U$.

Dado que $f$ es una función analítica en $U$, en particular es analítica en $z_0$, entonces, por la proposición 18.1 tenemos que:
\begin{equation*}
f(z) = f(z_0) + f'(z_0)(z-z_0) + \epsilon(z)(z-z_0),
\end{equation*}donde la función $\epsilon(z)$ es continua en $z_0$ y $\lim\limits_{z\to z_0} \epsilon(z) = 0$.

Sea $g(z):= f(z_0) + f'(z_0)(z-z_0)$. Es claro que $g$ es una función continua en $U$ con primitiva:
\begin{equation*}
G(z) = f(z_0)z + \frac{f'(z_0)}{2}(z-z_0)^2,
\end{equation*}entonces, como $\partial R^{(n)}$ es un contorno cerrado, de las proposiciones 34.2(3) y 35.1 se sigue que:
\begin{align*}
\int_{\partial R^{(n)}} f(z) dz & = \int_{\partial R^{(n)}} g(z) dz + \int_{\partial R^{(n)}} \epsilon(z)(z-z_0) dz\\
& = 0 + \int_{\partial R^{(n)}} \epsilon(z)(z-z_0) dz\\
& = \int_{\partial R^{(n)}} \epsilon(z)(z-z_0) dz.
\end{align*}

Puesto que $\lim\limits_{z\to z_0} \epsilon(z) = 0$, entonces dado $\varepsilon>0$ existe $\delta>0$ tal que:
\begin{equation*}
|z-z_0|<\delta \quad \Longrightarrow \quad |\epsilon(z)|<\frac{2}{L^2} \varepsilon.
\end{equation*}

Es claro que $\lim\limits_{n\to\infty} d_n = 0$, por lo que podemos fijar un índice $n$ tal que $d_n < \delta$. Además, como $z_0 \in R_n$ y para todo $z\in R_n$ se cumple que $|z-z_0|\leq d_n$, tenemos que $R_n \subset B(z_0\delta)$.

Dado que para todo $z\in \partial R^{(n)}$ se cumple que:
\begin{equation*}
|z-z_0|<\frac{L_n}{2} = \frac{L}{2^{n+1}},
\end{equation*}además $\displaystyle \int_{\partial R^{(n)}} |dz| = \ell(\partial R^{(n)}) = L_n$, entonces, considerando (35.1), (35.2) y la proposición 34.3(5), tenemos que:
\begin{align*}
\left|\int_{\partial R} f(z) dz\right| & \leq 4^n \left |\int_{\partial R^{(n)}} f(z) dz \right|\\
& = 4^n \left|\int_{\partial R^{(n)}} \epsilon(z)(z-z_0) dz\right|\\
& \leq 4^n \int_{\partial R^{(n)}} \left|\epsilon(z) \right| \left|(z-z_0)\right| |dz|\\
& \leq 4^n \frac{2 \varepsilon }{L^2} \frac{L}{2^{n+1}} L_n\\
& = 4^n \frac{2 \varepsilon }{L^2} \frac{L}{2^{n+1}} \frac{L}{2^{n}}\\
& = \varepsilon.
\end{align*}

Como $\varepsilon>0$ es arbitrario, entonces:
\begin{equation*}
\left|\int_{\partial R} f(z) dz\right| = 0 \quad \Longrightarrow \quad \int_{\partial R} f(z) dz = 0.
\end{equation*}

$\blacksquare$

Observación 35.5.
El lema de Goursat puede ser modificado para un triángulo cerrado $\triangle$ en $U$, es decir, considerando la frontera $\partial \triangle$ de dicho triángulo, se cumple que:
\begin{equation*}
\int_{\partial \triangle} f(z) dz = 0.
\end{equation*}

Más aún, si $P\subset U$ es un polígono y $\partial P$ su frontera, es claro que se tiene un contorno poligonal, en tal caso se cumple que:
\begin{equation*}
\int_{\partial P} f(z) dz = 0,
\end{equation*}ya que es posible agregar lados internos en $P$ hasta que su interior se subdivida en un número finito de triángulos, entonces con la modificación del lema de Goursat se tiene que la integral alrededor de cada triángulo es cero. Como la suma de las integrales a lo largo de las fronteras de todos estos triángulos es igual a la integral alrededor del contorno poligonal, entonces el resultado se cumple para el contorno poligonal.

En general, siguiendo este camino, se puede probar el resultado para un contorno cerrado simple arbitrario aproximando a dicho contorno lo suficientemente cerca con un contorno poligonal.

Observación 35.6.
Podemos mejorar el lema de Goursat permitiendo que la función $f$ no sea analítica en algunos puntos del interior del rectángulo imponiendo una condición adicional.

Lema 35.2. (Lema de Goursat generalizado.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $R\subset U$ un rectángulo cerrado, $z_1, z_2, \ldots z_n \in \operatorname{int} R$, $U’ := U\setminus\{z_1, z_2, \ldots z_n\}$ y $f:U’ \to \mathbb{C}$ una función analítica en $U’$ tal que:
\begin{equation*}
\lim_{z\to z_j} (z-z_j)f(z)=0,
\end{equation*}para todo $j=1,\ldots, n$. Entonces:
\begin{equation*}
\int_{\partial R} f(z) dz = 0.
\end{equation*}

Demostración. Dadas las hipótesis, notemos que es suficiente probar el caso para un único punto $z_0 \in \operatorname{int} R$, ya que por inducción se puede dividir a $R$ en pequeños rectángulos tales que cada uno contenga a lo más un punto interior $z_j$ de $R$, por lo que el caso general se deja como ejercicio al lector.

Dividimos a $R$ en nueve subrectángulos de modo que el rectángulo $R_0$ sea un cuadrado de lado $L$ y centro de simetría el punto $z_0 \in \operatorname{int} R$, como se muestra en la figura 133.

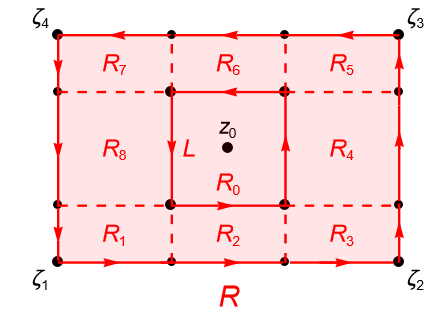
Dado que $f$ es analítica en $U\setminus\{z_0\}$ y $R_j\subset U\setminus\{z_0\}$ para todo $j=1,\ldots,8$, por el lema de Goursat , para esos ocho rectángulos $R_j$, tenemos que:
\begin{equation*}
\int_{\partial R_j} f(z) dz = 0,
\end{equation*}para todo $j=1,\ldots,8$.

Notemos que si orientamos positivamente a los nueve rectángulos, después de cancelar las integrales a lo largo de los segmentos de recta correspondientes con los lados en común de los rectángulos, como en la prueba del lema anterior, tenemos que:
\begin{align*}
\int_{\partial R} f(z) dz & = \int_{\partial R_0} f(z) dz + \sum_{j=1}^8 \int_{\partial R_j} f(z) dz\\
& = \int_{\partial R_0} f(z) dz + 0\\
& = \int_{\partial R_0} f(z) dz.
\end{align*}

Dado que $\lim\limits_{z\to z_0} (z-z_0) f(z)=0$, para $\varepsilon>0$ tenemos que existe $\delta>0$ tal que si $0<|z-z_0|<\delta$, entonces:
\begin{equation*}
|f(z)(z-z_0)|<\varepsilon \quad \Longrightarrow \quad |f(z)| < \frac{\varepsilon}{|z-z_0|}.
\end{equation*}

Más aún, para todo $z\in \partial R_0$ se cumple que:
\begin{equation*}
\frac{L}{2} \leq |z-z_0| \leq \frac{\sqrt{2} L}{2} \quad \Longrightarrow \quad \frac{1}{|z-z_0|} \leq \frac{2}{L}.
\end{equation*}

Además, por construcción:
\begin{equation*}
\int_{\partial R_0} |dz| = \ell(\partial R_0) = 4L.
\end{equation*}

Por lo que, de la proposición 34.3(5) se tiene que:
\begin{align*}
\left|\int_{\partial R} f(z) dz \right| & = \left|\int_{\partial R_0} f(z) dz\right|\\
& \leq \int_{\partial R_0} \left|f(z) \right| |dz|\\
& < \frac{2\varepsilon}{L} \int_{\partial R_0} |dz|\\
& = 8\varepsilon.
\end{align*}

Como $\varepsilon>0$ es arbitraria, entonces:
\begin{equation*}
\left|\int_{\partial R} f(z) dz \right| = 0 \quad \Longrightarrow \quad \int_{\partial R} f(z) dz =0.
\end{equation*}

$\blacksquare$

Tarea moral

1. Sean $R>0$ y $z_0\in\mathbb{C}$ fijo. Considera el contorno $C$ dado por la circunferencia $C(z_0, R)$ orientada positivamente.
   a) Evalúa la integral:
   \begin{equation*}
   \int_{C} \overline{z-z_0} \ dz.
   \end{equation*}b) Muestra que la función $f(z)=\overline{z}$ no tiene primitiva en ninguna región del plano complejo.
2. Considera a la integral:
   \begin{equation*}
   \int_{\gamma} \operatorname{Log}(z) dz,
   \end{equation*}donde $\gamma(t)=e^{it}$, para $t\in[0,\pi]$.
   
   Dado que $\operatorname{Log}(z)$ es discontinua en $-1$, entonces no es continua en $\gamma(\pi)$, por lo que no puede aplicarse la proposición 35.2.
   a) Muestra que $\operatorname{Log}(z) = \operatorname{Log}_{\left(\frac{-\pi}{2}, \frac{3\pi}{2}\right]}(z)$ para todo $z$ en el contorno $\gamma$.
   b) Conluye que:
   \begin{equation*}
   \int_{\gamma} \operatorname{Log}(z) dz = \int_{\gamma} \operatorname{Log}_{\left(\frac{-\pi}{2}, \frac{3\pi}{2}\right]}(z) dz,
   \end{equation*}y evalúa la integral del lado derecho utilizando la proposición 35.2.
3. Determina una primitiva para cada una de las siguientes funciones y específica la región dónde cada una de dichas primitivas están definidas.
   a) $\dfrac{1}{(z-1)(z+1)}$.
   b) $\dfrac{\operatorname{Log}(z)}{z}$.
   c) $ze^{z^2} – \dfrac{1}{z}$.
   d) $e^z\operatorname{cos}(z)$.
4. Evalúa cada una de las siguientes integrales.
   a) \begin{equation*}
   \displaystyle \int_{C} \left[(z-2-i)^2+\dfrac{i}{z-2-i}-\dfrac{3}{(z-2-i)^2}\right] dz,
   \end{equation*}donde $C$ es la circunferencia unitaria $C(0,1)$ orientada positivamente.
   b) $\displaystyle \int_{[z_1, z_2, z_3]} ze^z dz$, donde $z_1=\pi$, $z_2=-1$ y $z_3=-1-i\pi$.
   c) $\displaystyle \int_{[z_1, z_2, z_3]} \operatorname{Log}(z) dz$, donde $z_1=-i$, $z_2=1$ y $z_3=i$.
   d) $\displaystyle \int_{\gamma} \dfrac{1}{z} dz$, donde $\gamma$ es un contorno contenido en $\left\{z\in\mathbb{C} : \operatorname{Im}(z) < 0\right\}$ que une a $1-i$ y $-i$.
5. Sean $D\subset\mathbb{C}$ un dominio, $\gamma:[a,b]\subset\mathbb{R} \to D$, con $a<b$, una curva cerrada y $f:D\to\mathbb{C}$ una función analítica en $D$ con $f'(z)$ continua en $D$. Muestra que:
   \begin{equation*}
   I = \int_{\gamma} \overline{f(z)} f'(z) dz,
   \end{equation*}es un número imaginario puro.
6. Sea $\gamma_R$ la circunferencia $C(0,R)$ orientada positivamente, con $R>0$. Muestra que:
   \begin{equation*}
   \left| \int_{\gamma_R} \frac{\operatorname{Log}(z)}{z^2} dz \right| \leq 2\pi \left(\frac{\pi + \operatorname{Log}(R)}{R}\right).
   \end{equation*}
7. Sea $\triangle$ el triángulo con vértices $0,1$ e $i$. Evalúa las integrales $\displaystyle \int_{\partial \triangle} z dz$ y $\displaystyle \int_{\partial \triangle} \overline{z} dz$, donde $\partial \triangle$ es la frontera de $\triangle$ orientada positivamente.
8. Modifica la prueba del lema de Goursat para establecer lo siguiente: si $f$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$, entonces $\displaystyle \int_{\partial \triangle} f(z) dz = 0$, para cualquier triángulo cerrado $\triangle \subset U$.

Más adelante…

En esta entrada hemos probado algunos resultado importantes sobre las integrales de contorno como el Teorema Fundamental del Cálculo para el caso complejo y el lema de Goursat, que como veremos nos permitirá probar el Teorema de Cauchy para el caso en que se tiene un contorno cerrado arbitrario.

En la siguiente entrada probaremos algunas versiones del Teorema integral de Cauchy y abordaremos algunas de sus consecuencias más importantes, como la Fórmula Integral de Cauchy, el Teorema de Liouville, el Teorema Fundamental del Álgebra, entre otros. Además veremos un recíproco del Teorema de Cauchy conocido como el Teorema de Morera.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Integrales de contorno I.
• Siguiente entrada del curso: Teorema integral de Cauchy.