Introducción
Hemos llegado al punto en que presentaremos la integral de Riemann-Stieltjes. Antes de abordar el tema con resultados más abstractos y formales (que expondremos en las siguientes dos entradas del blog) motivaremos la definición con funciones distribución de probabilidad. Aunque no requerimos más que la idea de dicha función para entender esta sección, para un conocimiento más profundo podrías consultar las entradas:
Probabilidad I: Funciones de Distribución de Probabilidad,
Probabilidad I: Variables Aleatorias Discretas y
Probabilidad I: Variables Aleatorias Continuas.
Dada $\mathcal{X}$ una variable aleatoria, se conoce como función de distribución de $\mathcal{X}$ a la función $F_{\mathcal{X}}: \mathbb{R} \to \mathbb{R} \,$ definida como:
$$F_{\mathcal{X}}(x) := \mathbb{P}(\mathcal{X} \leq x)$$
es decir, la probabilidad de que la variable aleatoria tome valores menores o iguales que $x.$ Satisface lo siguiente:
- $\forall \, x \in \mathbb{R}, \, 0 \leq F_{\mathcal{X}}(x) \leq 1$
- Es continua por la derecha y tiene límite por la izquierda.
- Es no decreciente, es decir, si $x_1 \leq x_2$ entonces $F_{\mathcal{X}}(x_1) \leq F_{\mathcal{X}}(x_2).$
- $\underset{x \to \, -\infty}{F_{\mathcal{X}}(x)} = 0.$
- $\underset{x \to \, \infty}{F_{\mathcal{X}}(x)} = 1.$
Dependiendo las propiedades de la variable aleatoria, la función $F_\mathcal{X}$ puede ser de dos formas:
Si $\mathcal{X}$ es variable aleatoria discreta, entonces
$$F_{\mathcal{X}}(x) = \underset{t \leq x}{\sum}f(t).$$
Donde $f(t)$ es la probabilidad de que $\mathcal{X}$ tome el valor $t$, la cual es distinta de cero solamente para un conjunto a lo más numerable de valores $t.$
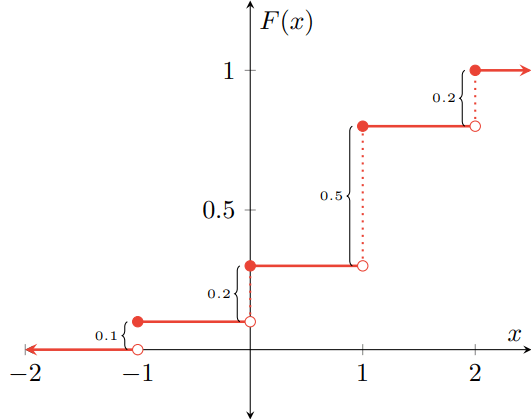
Como ejemplo, uno tomado de Probabilidad I: Variables Aleatorias Discretas.
\begin{equation*}
F_{\mathcal{X}}(x)=\begin{cases}
0 \, \text{ si $x< -1$}\\
\\
0.1 \, \text{ si $-1 \leq x < 0$}\\
\\
0.3 \, \text{ si $0 \leq x < 1$}\\
\\
0.8 \, \text{ si $1 \leq x < 2$}\\
\\
1 \, \text{ si $2 \leq x$}\\
\end{cases}
\end{equation*}
Si $\mathcal{X}$ es variable aleatoria continua, entonces
$$F_{\mathcal{X}}(x) = \int_{- \infty}^{x}f(t)dt.$$
Donde $f(t)$ es la probabilidad de que $\mathcal{X}$ tome el valor $t$, la cual es distinta de cero solamente para un conjunto a lo más numerable de valores $t.$
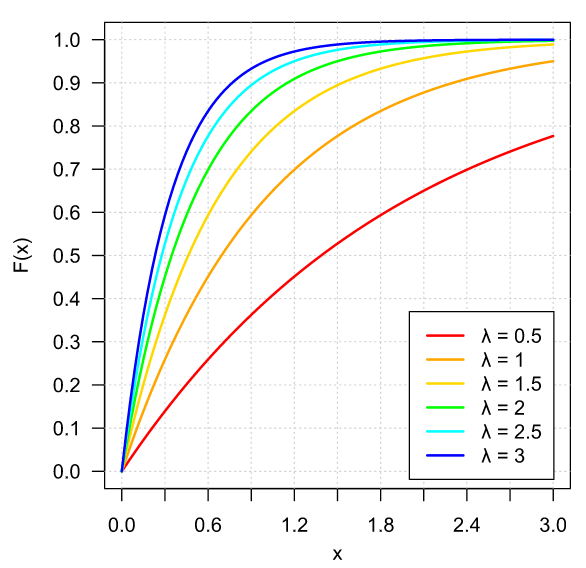
Como ejemplo, uno tomado de Probabilidad I: Variables Aleatorias Continuas
\begin{equation*}
F_{\mathcal{X}}(x)= \begin{cases}
1 \, – \, e^{-\lambda x} \, \text{ si $x \geq 0,$}\\
\\
0 \, \text{ en otro caso.}
\end{cases}
\end{equation*}
Donde la función densidad está dada por:
\begin{equation*}
f(x)=
\begin{cases}
\lambda e^{-\lambda x} \, \text{ si $x \geq 0,$}\\
\\
0 \, \text{ en otro caso.}
\end{cases}
\end{equation*}
Podríamos preguntarnos si es posible definir una integral que muestre el valor de la función, sin importar el tipo de variable aleatoria.
En los cursos de cálculo se habla del concepto de integral de Riemann de una función $f:[a,b] \to \mathbb{R}, \, a,b \in \mathbb{R}.$ A partir de una partición $P= \{x_0= a,…, x_n = b\}$ se define la suma de Riemann como
$$S(P,f) = \sum_{i =1}^{n} f(\xi_i)(x_i \, – \, x_{i-1})$$
donde $\xi_i \in [x_{i-1}, x_i] \,$ y
$$\, S(P,f) \to \int_{a}^{b}f(x) \, dx \,$$
cuando $\, n \to \infty.$
La integral de Riemann-Stieltjes generaliza esta idea, modificando los intervalos generados por la partición a través de una función $\alpha:[a,b] \to \mathbb{R}.$
Definición. Suma de Riemann-Stieltjes. Sean $f:[a,b] \to \mathbb{R}, \,$ $\alpha:[a,b] \to \mathbb{R} \,$ funciones y $P= \{x_0=a,…,x_n=b\}$ una partición de $[a,b].$ Definimos la suma de Riemann-Stieltjes de $P$ con respecto a $f$ y $\alpha$ como
\begin{align}
S(P,f,\alpha) := \sum_{i =1}^{n} f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1}))
\end{align}
Definición. Integral de Riemann-Stieltjes. Sean $f, \, \alpha$ y $P\, $ como en la definición anterior. Si existe el límite en $S(P,f, \alpha)$ cuando $n \to \infty,$ se define y denota a la integral de Riemann-Stieltjes como
\begin{align}
\int_{a}^{b}f(x) \, d \alpha := \underset{n \to \infty}{lim} \, \sum_{i =1}^{n} f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1}))
\end{align}
Para visualizar las ideas, consideremos los siguientes:
Ejemplos
En cualquier caso, $\alpha:[a,b] \to \mathbb{R}.$
- $\alpha(x) = x.$ En este caso coincide con la integral de Riemann. Evidentemente:
\begin{align*}
\int_{a}^{b}f(x) \, d \alpha := \underset{n \to \infty}{lim} \, \sum_{i =1}^{n} f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1})) = \underset{n \to \infty}{lim} \, \sum_{i =1}^{n} f(\xi_i)(x_i \, – \, x_{i-1}).
\end{align*} - Si $\alpha(x) = F_{\mathcal{X}}(x)$ es la función de distribución de $\mathcal{X},$ entonces la integral de Riemman-Stieltjes es la esperanza de la variable aleatoria $Y=f(\mathcal{X}).$
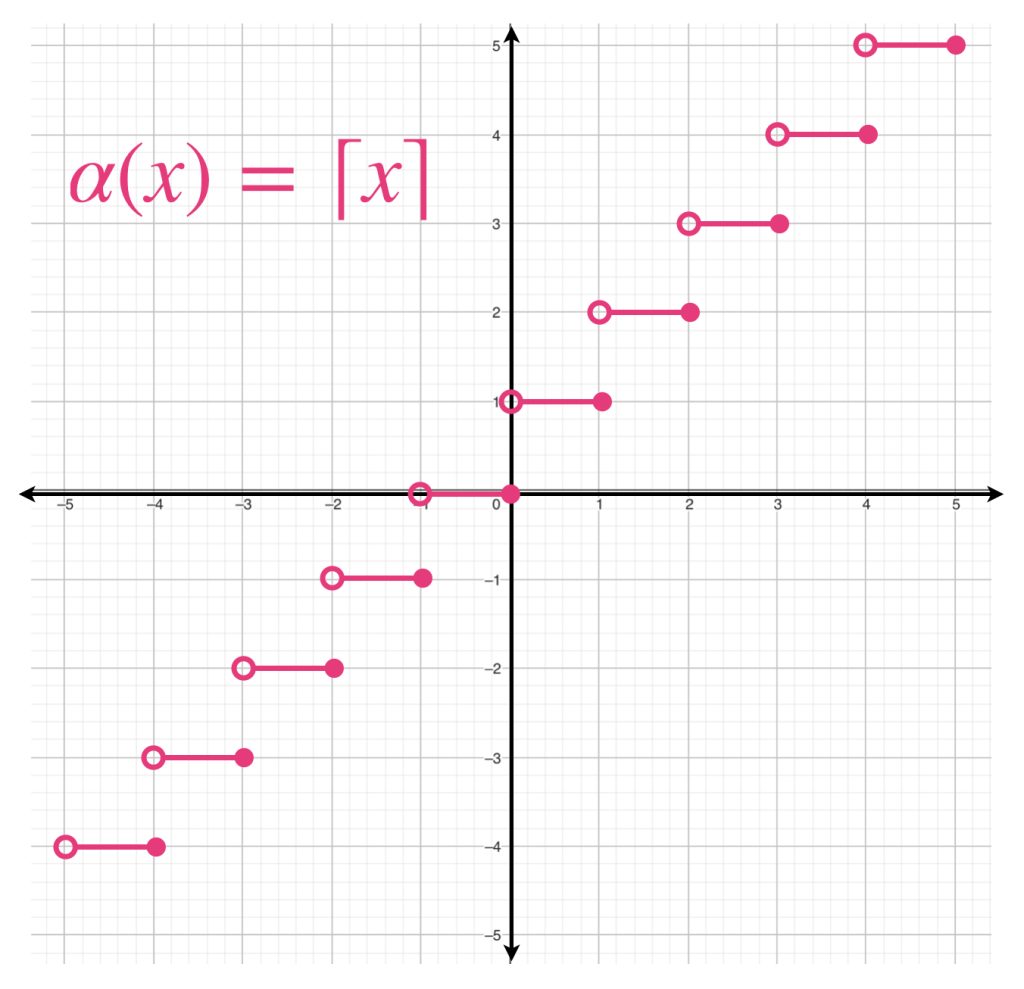
- $\alpha(x) = \lceil x \rceil.$ La función techo, es decir:
\begin{align*}
\lceil x \rceil = {\text{mín} \,} \{k \in \mathbb{Z} : k \geq x\}
\end{align*}
Analicemos más esta última función. Sea $P= \{x_0 = a,…,x_n =b\}$. Entonces para cada $i=0,…,n$
$$\alpha(x_i) \, – \, \alpha(x_{i-1}) = \lceil x_i \rceil \, – \, \lceil x_{i-1} \rceil$$
Si suponemos que los intervalos son muy pequeños, podemos pedir que $|P|<1.$ En esta situación dos puntos consecutivos de la partición podrían estar entre dos enteros consecutivos o bien, tener un entero entre ellos. Así tenemos dos casos:
- \begin{align*}
\lceil x_i \rceil &= \lceil x_{i-1} \rceil\\
\Rightarrow \, \lceil x_i \rceil \, – \, \lceil x_{i-1} \rceil &= 0
\end{align*}
o bien - \begin{align*}
\lceil x_i \rceil &> \lceil x_{i-1} \rceil \, \\
\Rightarrow \, \lceil x_i \rceil \, – \, \lceil x_{i-1} \rceil &= 1.
\end{align*}
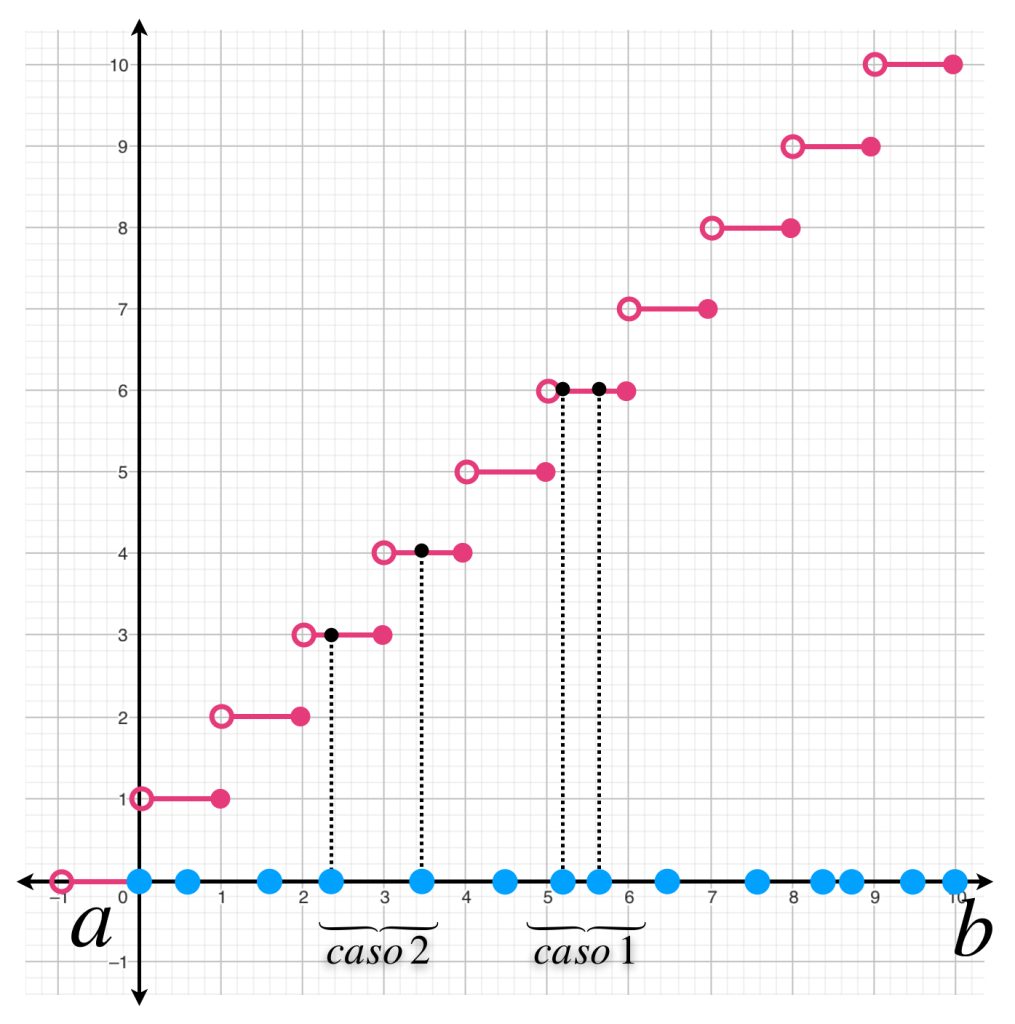
En consecuencia, si $\xi_i \in [x_{i-1}, x_i]$ entonces cada sumando toma los siguientes valores:
En el caso 1. $f(\xi_i)(\lceil x_i \rceil \, – \, \lceil x_{i-1} \rceil) = 0.$
En el caso 2. $f(\xi_i)(\lceil x_i \rceil \, – \, \lceil x_{i-1} \rceil) = f(\xi_1).$
La siguiente imagen permite visualizar este comportamiento.
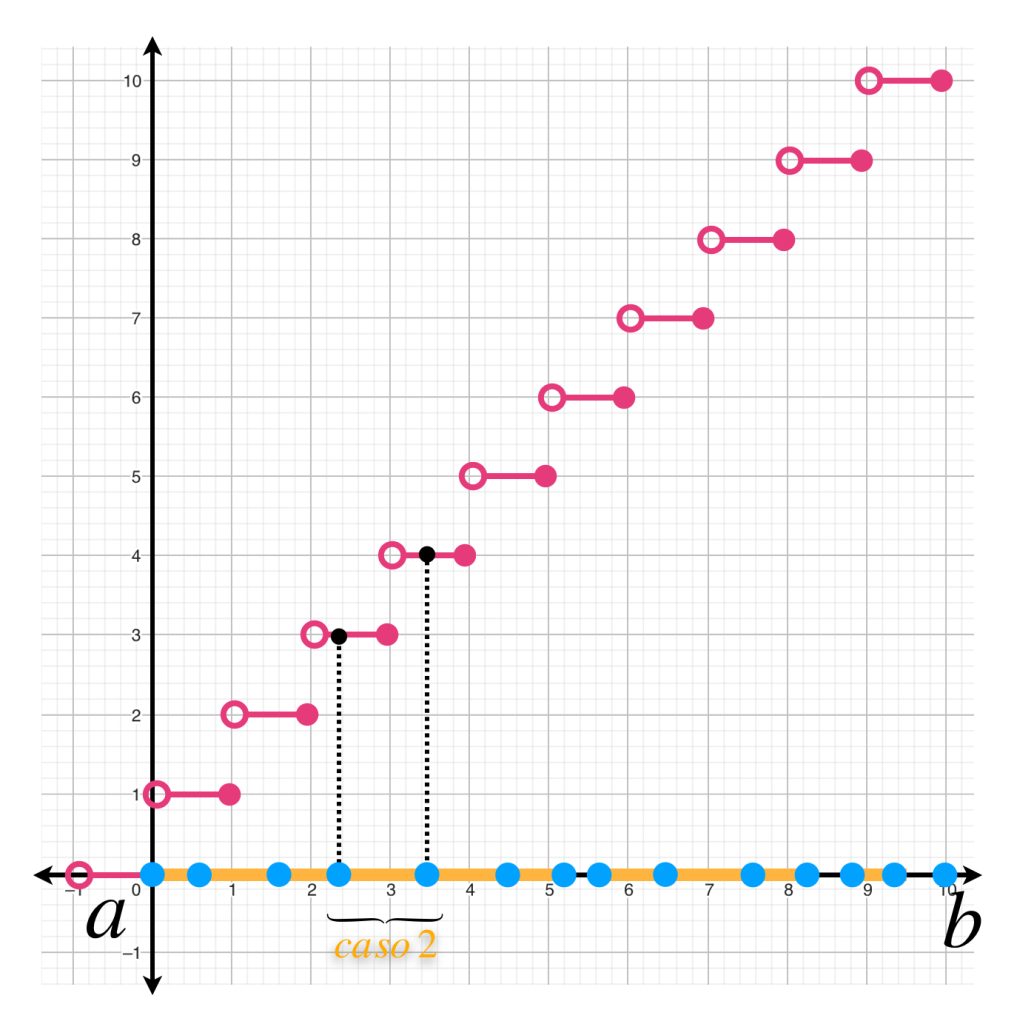
Calculemos $\int_{0}^{10}1 \, d \, \lceil x \rceil.$
En esta situación, los únicos sumandos significativos serán los que tienen algún entero en $\{1,2,…,10\}.$ Por lo tanto
$\int_{0}^{10}1 \, d \, \lceil x \rceil = \sum_{i=1}^{10} 1 = 10.$
¿Puedes calcular $\int_{0}^{10}f(x) \, d \, \lceil x \rceil,$ para cualquier $f$ continua en $[0,10]?$
Generaliza aún más y calcula $\int_{a}^{b}f(x) \, d \, \lceil x \rceil$ para cualquier intervalo $[a,b].$ $\textcolor{orange}{(\text{Ejercicio como tarea moral).}}$
En las siguientes entradas veremos que se satisface:
Proposición: Si $f$ es continua en $[a,b]$ y $\alpha$ es monótona, existe $\int_{a}^{b} f(x) \, d \alpha.$
Con la integral de Riemann-Stieltjes es posible identificar las funciones de distribución de variables aleatorias, sin importar si la variable es discreta, continua o una «mezcla» de ambas.
Ejemplo
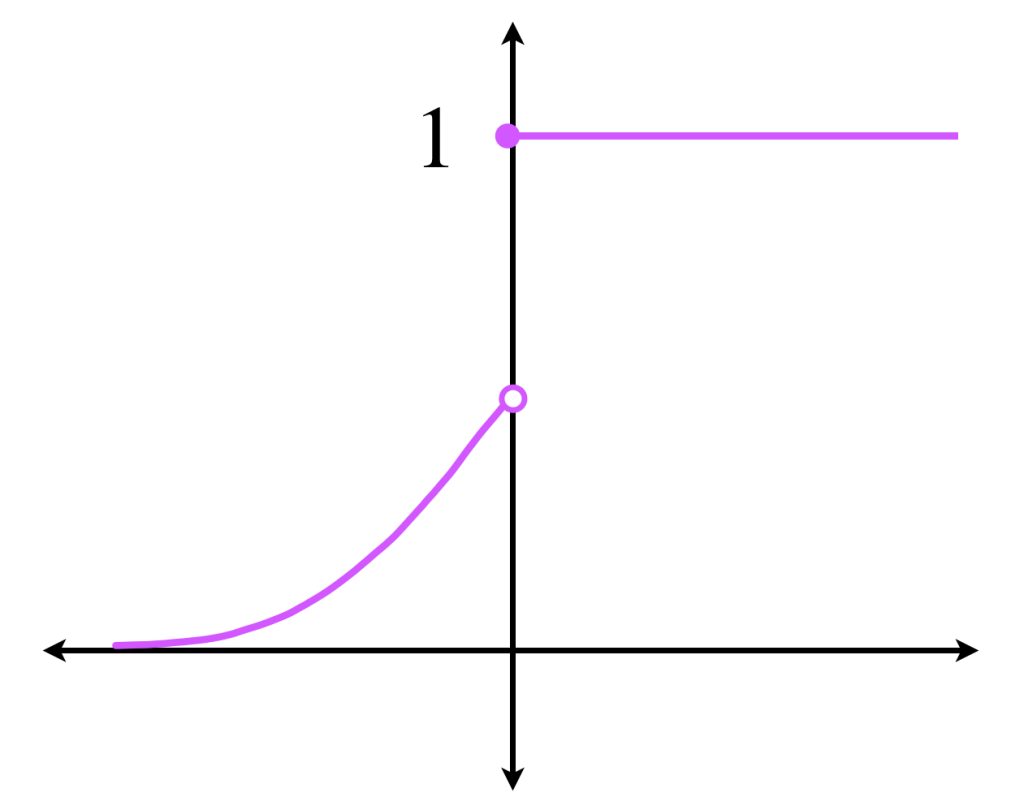
La siguiente expresión refleja el comportamiento de una variable aleatoria que es continua en un «pedazo» y discreta en el resto.
\begin{equation*}
\alpha(x) = \begin{cases}
\frac{1}{\sqrt{2 \pi}}\int_{-\infty}^{x} e ^{-\frac{t^2}{2}} dt \, &\text{ si $x<0$ }\\
\\
1 \, &\text{ si $x \geq 0$}
\end{cases}
\end{equation*}
Entonces, si $F_{\mathcal{X}}$ es la función distribución de la variable aleatoria descrita se satisface:
$F_{\mathcal{X}}(b) \, – \, F_{\mathcal{X}}(a) = \text{Probabilidad de que } \mathcal{X} \text{ tome valores en } [a,b] = \int_{a}^{b}1 \, d \alpha.$
La esperanza de una variable aleatoria puede expresarse con una integral de Riemann-Stieltjes
A continuación presentamos una definición de la esperanza con la integral que estamos conociendo y es equivalente a la usada convencionalmente. Para profundizar en la teoría, visitar Probabilidad I: Valor Esperado de una Variable Aleatoria
Definición. Esperanza de $\mathcal{X}.$ Sea $\mathcal{X}$ una variable aleatoria con función de distribución $\alpha(x).$ La esperanza de $\mathcal{X}$ es
$$E(\mathcal{X}) = \int_{-\infty}^{\infty}x \, d\alpha.$$
Ejemplos
Sea $\mathcal{X}$ variable aleatoria con distribución binomial, $n=3, \, p= \frac{1}{2}.$ Dado que
$$\mathbb{P}(\mathcal{X} = k) = \binom{3}{k}\frac{1}{2}^k\frac{1}{2}^{3-k}$$
Se sigue:
$\mathbb{P}(\mathcal{X} = 0) = \frac{1}{8}$
$\mathbb{P}(\mathcal{X} = 1) = \frac{3}{8}$
$\mathbb{P}(\mathcal{X} = 2) = \frac{3}{8}$
$\mathbb{P}(\mathcal{X} = 3) = \frac{1}{8}$
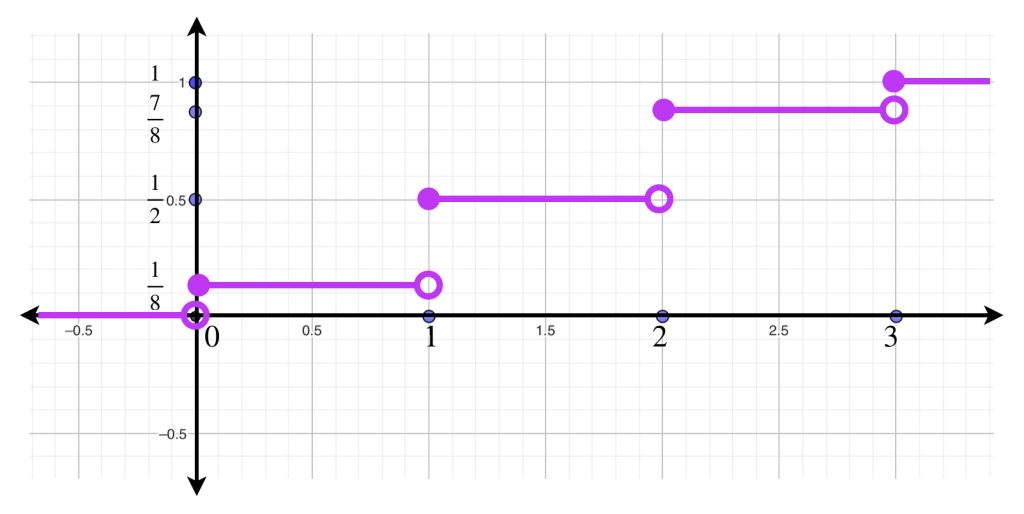
Y así, la función distribución es:
\begin{equation*}
F_{\mathcal{X}} =\begin{cases}
0 \, &\text{ si }&x < 0 \\
\\
\frac{1}{8} \, &\text{ si $0\leq$} &x < 1 \\
\\
\frac{1}{2} \, &\text{ si $1 \leq$} &x < 2 \\
\\
\frac{7}{8} \, &\text{ si $2 \leq$} &x < 3 \\
\\
1 \, &\text{ si $3 \leq$} &x \\
\end{cases}
\end{equation*}.
Y la esperanza es
\begin{align*}
\sum_{k=0}^{3}k \, \mathbb{P}(\mathcal{X} = k) &= (0)\left(\frac{1}{8}\right) + (1)\left(\frac{3}{8}\right) + (2)\left(\frac{3}{8}\right) + (3)\left(\frac{1}{8}\right) \\
&=\frac{6}{4}
\end{align*}
Dejaremos como $\textcolor{orange}{\text{ejercicio de tarea moral,}}$ verificar la integral de Riemann-Stieltjes
\begin{align*}
\int_{\infty}^{\infty}x \, d\alpha &= \int_{-\infty}^{0}x \, d\alpha + \int_{0}^{3}x \, d\alpha + \int_{3}^{\infty}x \, d\alpha\\
&=0 + \dfrac{6}{4} +0\\
&= \dfrac{6}{4}.
\end{align*}
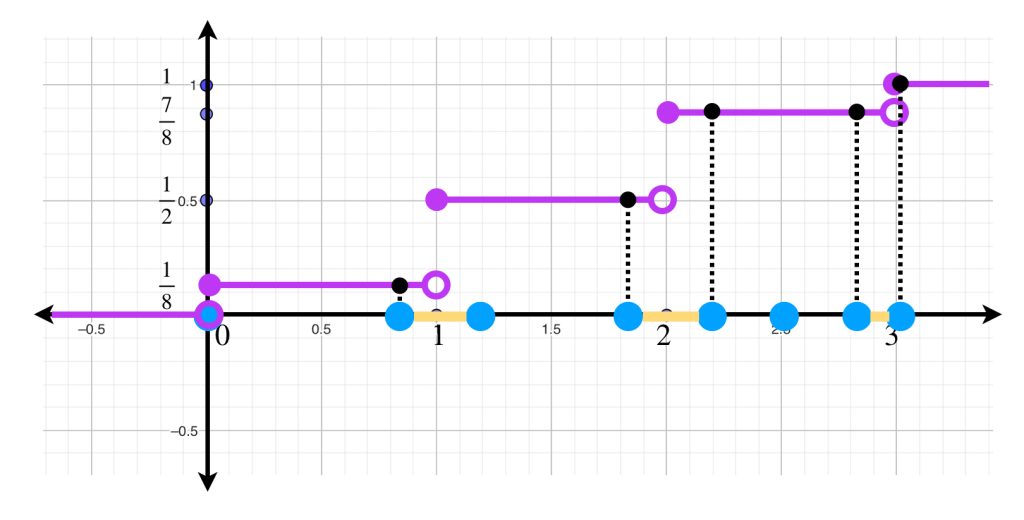
Como sugerencia, verifica que en una partición de $[0,3]$ con intervalos muy pequeños $(\delta< 1)$ los únicos sumandos que no se anulan en la suma de Riemann-Stieltjes serán los correspondientes a intervalos que tienen algún entero en $\{0,1,2,3\}.$
Otro ejemplo para terminar esta sección
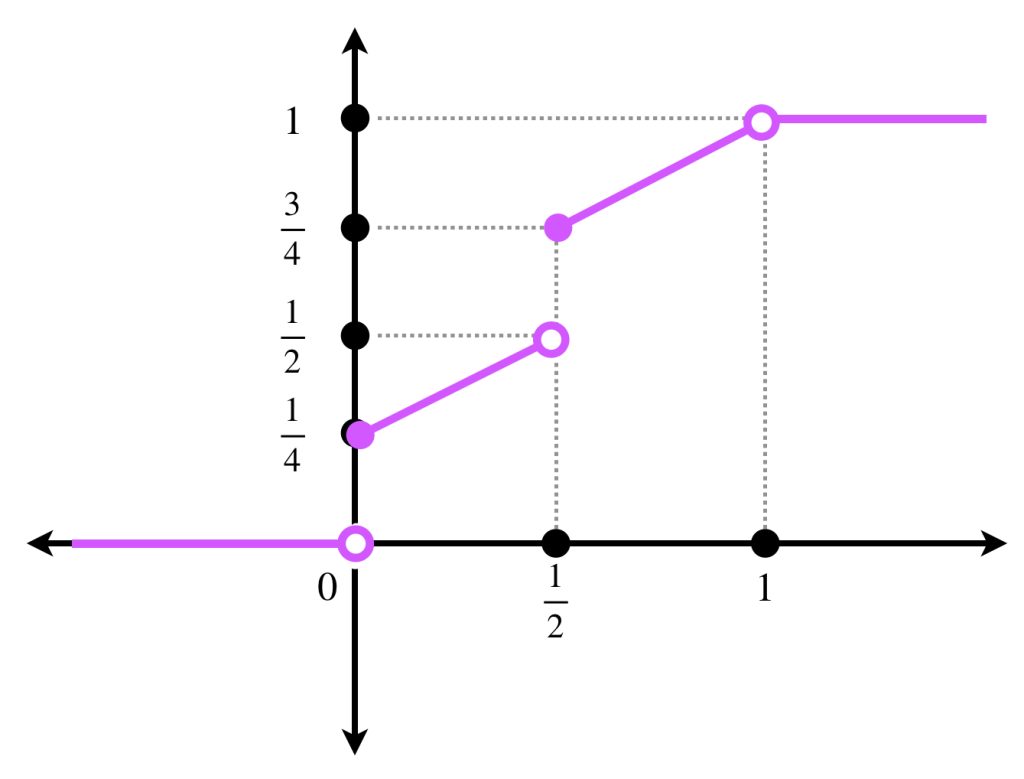
Ahora supongamos que la función de distribución de una variable aleatoria está dada por:
\begin{equation*}
F_{\mathcal{X}}(x) =\begin{cases}
0 \, &\text{ si }&x < 0 \\
\\
\frac{x}{2}+\frac{1}{4} \, &\text{ si $0\leq$} &x < \frac{1}{2} \\
\\
\frac{x}{2}+\frac{1}{2} \, &\text{ si $\frac{1}{2} \leq$} &x < 1 \\
\\
1 \, &\text{ si $1 \leq$} &x \\
\end{cases}
\end{equation*}.
Vamos a calcular la esperanza de $\mathcal{X}$ por medio de:
$$\int_{-\infty}^{\infty}x \, d\alpha.$$
Los detalles se dejarán como $\textcolor{orange}{\text{ejercicios de tarea moral.}}$ Nota que
$$\int_{-\infty}^{\infty}x \, d\alpha= \textcolor{PineGreen}{\int_{-\infty}^{0}x \, d\alpha} \textcolor{blue}{+ \int_{0}^{\frac{1}{2}}x \, d\alpha + \int_{\frac{1}{2}}^{1}x \, d\alpha} \textcolor{PineGreen}{+ \int_{1}^{\infty}x \, d\alpha}.$$
Primero vamos a obtener
$$ \textcolor{blue}{\int_{0}^{\frac{1}{2}}x \, d\alpha}.$$
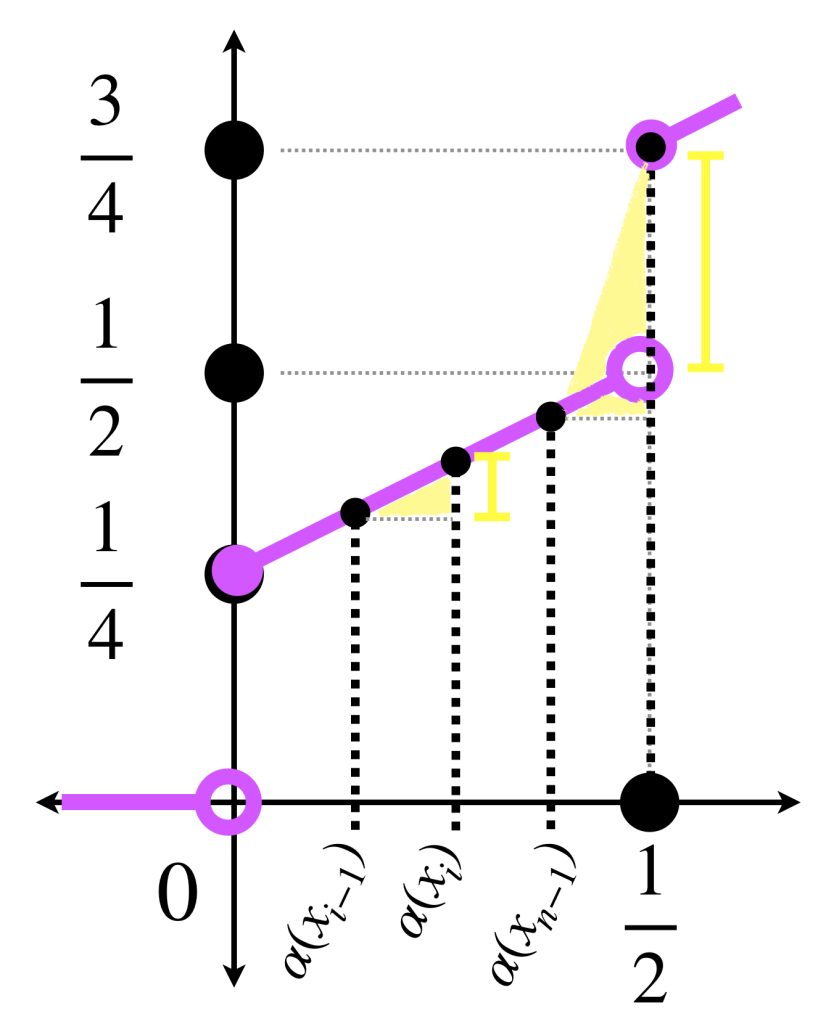
Sea $P= \{x_0=0,…,x_{n-1},x_n= \frac{1}{2}\}$ una partición de $[0,\frac{1}{2}].$ Calculemos
\begin{align}
\sum_{i=1}^{n}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1}))= \sum_{i=1}^{n-1}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1})) + f(\xi_n)(\alpha(\frac{1}{2}) \, – \, \alpha(x_{n-1}))
\end{align}
Observa que todos los intervalos a excepción del último cumplen que
\begin{align*}
\alpha(x_i) \, – \, \alpha(x_{i-1}) &= \left(\frac{x_i}{2}+\frac{1}{4}\right) \, – \, \left(\frac{x_{i-1}}{2}+\frac{1}{4}\right)\\
&= \frac{x_i \, – \, x_{i-1}}{2}
\end{align*}
Entonces
\begin{align*}
\sum_{i=1}^{n-1}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1})) &= \sum_{i=1}^{n-1}f(\xi_i)\left( \frac{x_i \, – \, x_{i-1}}{2}\right)\\
&=\frac{1}{2} \sum_{i=1}^{n-1}f(\xi_i)(x_i \, – \, x_{i-1})
\end{align*}
De modo que
\begin{align}
\nonumber \underset{n\to \infty}{lim}\, \sum_{i=1}^{n-1}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1})) &= \frac{1}{2}\int_{0}^{\frac{1}{2}}x \, dx \\
\nonumber &= \frac{1}{2} \frac{x^2}{2}\Big|_{0}^{\frac{1}{2}}\\
&= \frac{1}{16}.
\end{align}
En cuanto al último intervalo, cuando el tamaño de este tiende a $0$ se satisface
\begin{align}
f(\xi_n)(\alpha(\frac{1}{2}) \, – \, \alpha(x_{n-1})) \, \, \to \frac{1}{2}\left(\frac{3}{4} \, – \, \frac{1}{2}\right) = \frac{1}{8}
\end{align}
Por lo tanto, haciendo $n \to \infty$ en (3) por (4) y (5) tenemos:
\begin{align}
\textcolor{blue}{\int_{0}^{\frac{1}{2}}x \, d\alpha}= \frac{1}{16}+\frac{1}{8} = \frac{3}{16}
\end{align}
Análogamente se puede verificar que también
\begin{align}
\textcolor{blue}{\int_{\frac{1}{2}}^{1}x \, d\alpha}= \frac{3}{16}
\end{align}
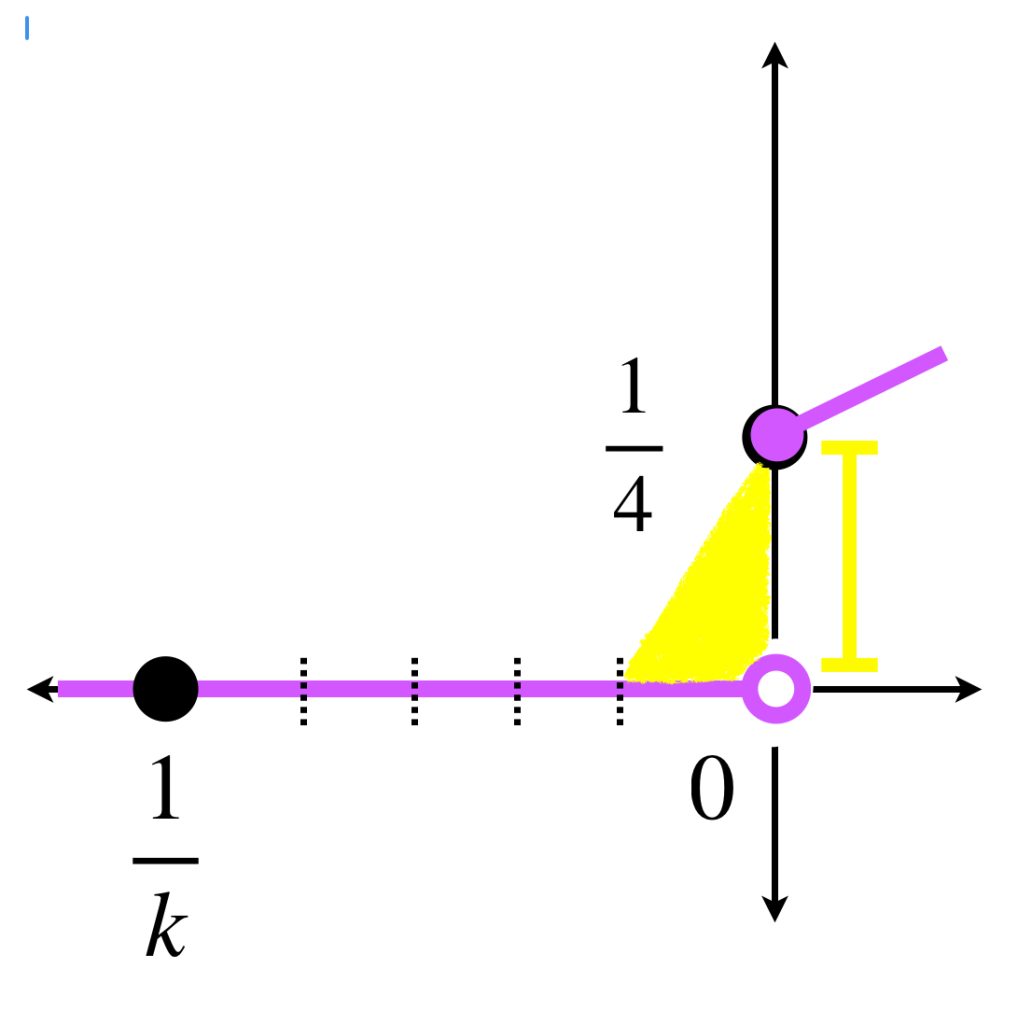
En cuanto a la integral $\int_{-\infty}^{0}x \, d\alpha \,$ nota que eligiendo $\frac{1}{k}$ muy pequeñito podemos separarla como
\begin{align}
\int_{-\infty}^{0}x \, d\alpha = \int_{-\infty}^{-\frac{1}{k}}x \, d\alpha + \int_{-\frac{1}{k}}^{0}x \, d\alpha
\end{align}
Evidentemente, la primera parte $\int_{-\infty}^{-\frac{1}{k}}x \, d\alpha \,$ se anula. La otra integral $\int_{-\frac{1}{k}}^{0}x \, d\alpha \,$ se puede calcular con sumas de Riemann-Stieltjes: Si $P=\{x_0= \frac{1}{k},…,x_n=0\}$ es una partición de $[\frac{1}{k},0]$ el único sumando significativo es el último donde $f(\xi_n)(\alpha(x_{0}) \, – \, \alpha(x_{n-1})) \, \to \, 0(\frac{1}{4} \, – \, 0)=0.$
Por lo tanto
\begin{align}
\textcolor{PineGreen}{\int_{-\infty}^{0}x \, d\alpha = 0}.
\end{align}
Es sencillo comprobar que también
\begin{align}
\textcolor{PineGreen}{\int_{1}^{\infty}x \, d\alpha = 0}.
\end{align}
Y así, de (6), (7),(9) y (10) concluimos que
\begin{align}
\int_{-\infty}^{\infty}x \, d\alpha = \frac{6}{16}= \frac{3}{8}.
\end{align}
Más adelante…
Veremos resultados formales de la integral de Riemann-Stieltjes y algunas de sus propiedades.
Tarea moral
- Resuelve los detalles pendientes de esta entrada que se fueron indicando.
- Sea $\alpha:[a,b] \to \mathbb{R}\, $ una función escalonada, calcula $\int_{a}^{b}f \, d\alpha$ con $f:[a,b] \to \mathbb{R}$ continua.
Enlaces
- Análisis Matemático.
- Enlace a entrada anterior.
- Enlace a entrada siguiente.