$\textit{MATERIAL EN REVISIÓN}$
Introducción
Usaremos los resultados vistos en las entradas anteriores Enunciado del teorema de Stone-Weierstrass y primera parte de la demostración y Segunda parte de la demostración del teorema de Stone-Weierstrass para culminar con la demostración del teorema de Stone-Weierstrass. Sin más preámbulo, recordemos lo que dice.
Teorema. Stone-Weierstrass: Sea $K$ un espacio métrico compacto. Sea $A \subset \mathcal{C}^0(K, \mathbb{R}),$ es decir, $A$ es un conjunto de funciones continuas de $K$ en $\mathbb{R}.$ Si $A$ satisface las siguientes propiedades:
a) Para cada $\lambda, \mu \, \in \mathbb{R}$ y $f,g \in A$ se cumple que $$\lambda f + \mu g \, \in A.$$ Esto es, $A$ es cerrado bajo combinaciones lineales.
b) Para cada $f,g \in A$ se cumple que $$f \cdot g \, \in A.$$ Esto es, $A$ es cerrado bajo producto de funciones.
c) $1 \in A,$ donde $1$ es la función constante que para cada $x \in K$ asigna el valor $1.$
d) Para cualesquiera $x_1, x_2 \in K$ tales que $x_1 \neq x_2$ existe una función $\varphi \in A$ tal que $\varphi (x_1) \neq \varphi(x_2).$
Entonces $A$ es denso en $\mathcal{C}^0(K, \mathbb{R}),$ es decir, $\overline{A}=\mathcal{C}^0(K, \mathbb{R}).$
Demostración:
Sea $A$ como en las hipótesis. Para probar que $\overline{A}=\mathcal{C}^0(K, \mathbb{R})$ tomemos $f \in \mathcal{C}^0(K, \mathbb{R}).$
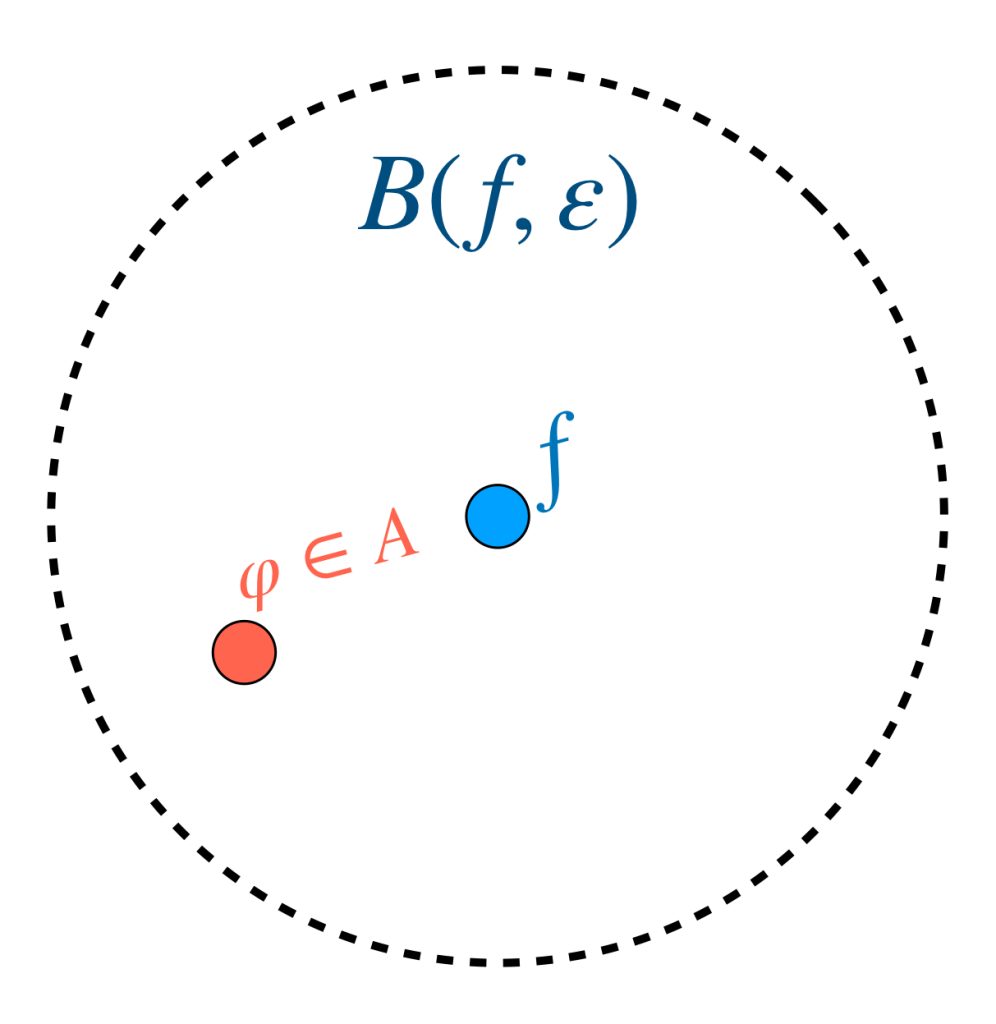
Sea $\varepsilon >0.$ Demostraremos que para toda $B(f,\varepsilon)$ se cumple que existe una función $\varphi \in A$ tal que $\varphi \in B(f,\varepsilon),$ es decir
$$d_\infty(f,\varphi)< \varepsilon.$$
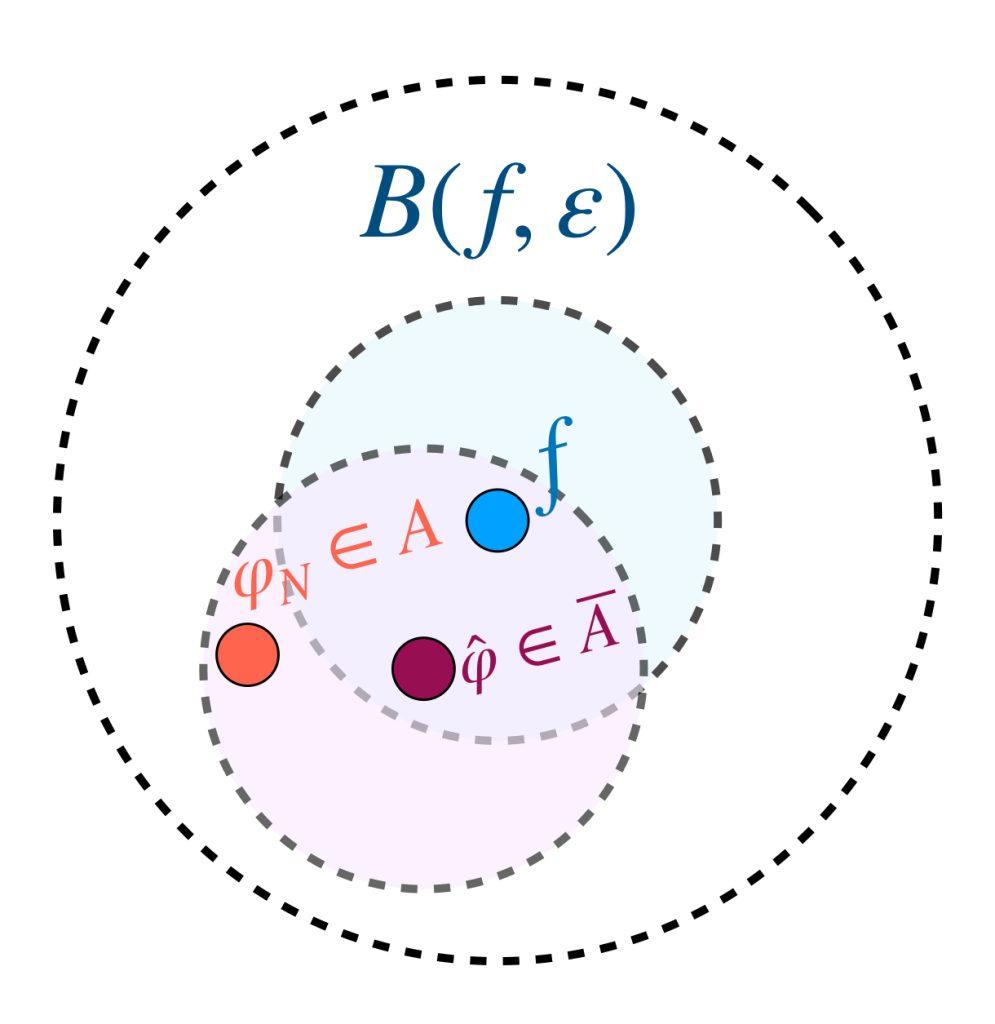
Para que dicha $\varphi \in A$ exista, es suficiente demostrar que existe $\textcolor{purple}{\hat{\varphi}} \in \overline{A}$ tal que
$$d_\infty(f,\hat{\varphi}) < \frac{\varepsilon}{2}.$$
Pues si esa $\hat{\varphi} \in \overline{A}$ existe, entonces por lo visto en la entrada Convergencia, existe también una sucesión $(\varphi_n)_{n \in \mathbb{N}}$ de funciones en $A$ tales que $\varphi_n \to \hat{\varphi}$ en $\mathcal{C}^0(K, \mathbb{R})$ y así existe $N \in \mathbb{N}$ tal que
$$d_\infty(\hat{\varphi},\varphi_N) < \frac{\varepsilon}{2}.$$
En consecuencia las desigualdades
\begin{align*}
d_\infty(f,\varphi_N) &\leq d_\infty(f,\hat{\varphi}) +d_\infty(\hat{\varphi},\varphi_N) \\
&< \frac{\varepsilon}{2} + \frac{\varepsilon}{2}\\
&< \varepsilon,
\end{align*}
evidenciarían la existencia de la $\varphi$ deseada. Procedamos entonces a justificar la existencia de la $\hat{\varphi} \in \overline{A}$ descrita arriba.
Fijemos $x \in K.$ Por el lema 1, visto en Enunciado del teorema de Stone-Weierstrass y primera parte de la demostración sabemos que para cada $y \in K$ existe $\varphi_{x,y} \in A$ (que depende de $x$ y de $y$) tal que
\begin{align}
\textcolor{blue}{\varphi_{x,y} (x)} & \textcolor{blue}{= f(x)}, \, \text{ y} \\
\textcolor{magenta}{\varphi_{x,y} (y)} &\textcolor{magenta}{= f(y)}.
\end{align}
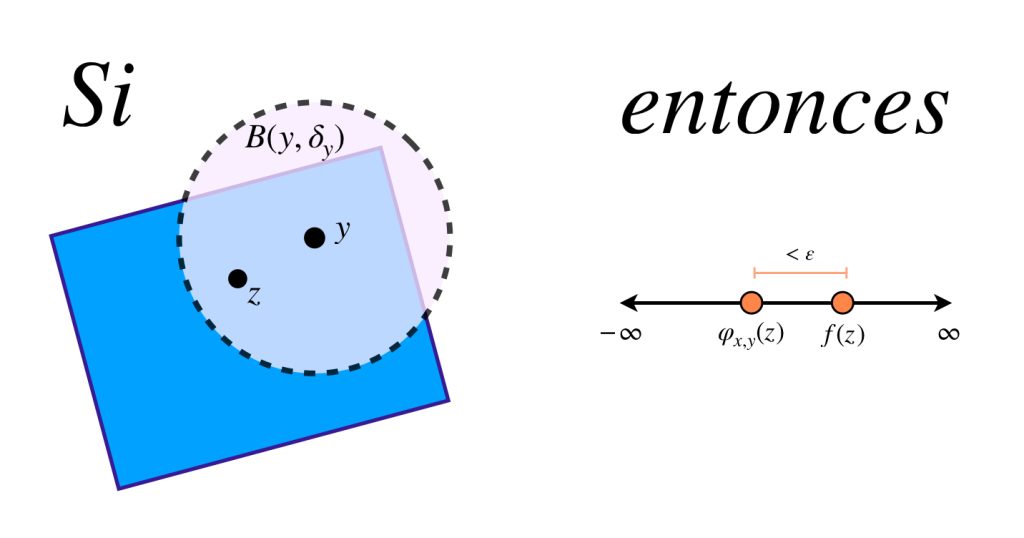
Sea $\varepsilon >0.$ Como tanto $\varphi_{x,y}$ como $f$ son continuas en $K,$ entonces la función $\varphi_{x,y}\, – \, f$ es continua en $K.$ Así, para cada $y \in K$ existe $\delta_y >0$ tal que si $z \in B(y,\delta_y)$ entonces
\begin{align}
\nonumber &&|(\varphi_{x,y}\, – \, f)(z) \, – \, (\varphi_{x,y}\, – \, f)(y)| &< \varepsilon \\
\nonumber &\Rightarrow&|\varphi_{x,y}(z)\, – \, f(z) \,- \textcolor{magenta}{ ( \varphi_{x,y}(y)\, – \, f(y))}|&< \varepsilon \\
\nonumber &\Rightarrow&\ |\varphi_{x,y}(z)\, – \, f(z) \, \textcolor{magenta}{- 0}|&< \varepsilon \\
&\Rightarrow& |\varphi_{x,y}(z)\, – \, f(z)|&< \varepsilon
\end{align}
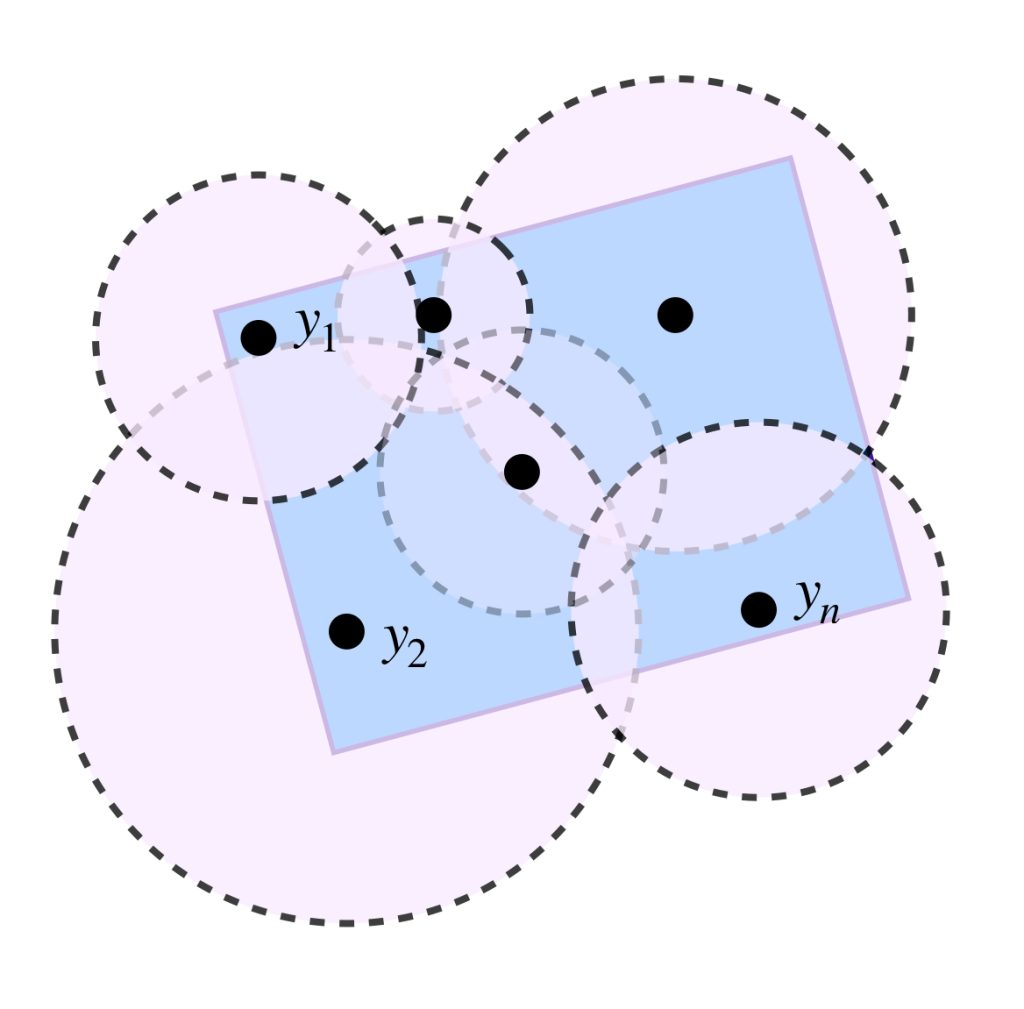
La colección de bolas abiertas de radio $\delta_y$ y centro en la respectiva $y \in K: \, $$\, \{B(y, \delta_y)\}_{y \in K}$ es una cubierta abierta de $K$ que recordemos es compacto. Así, existe una subcubierta finita de $ \{B(y, \delta_y)\}_{y \in K},$ es decir, existen
$y_1, \, y_2,…, y_n \in K$ con $n \in \mathbb{N}$ tales que $\{B(y_1, \delta_{y_1}), \, B(y_2, \delta_{y_2}),…,B(y_n, \delta_{y_n})\}$ es una cubierta abierta de $K.$
Sea
$$\varphi_x = \text{mín}\{\varphi_{x,y_1}, \, \varphi_{x,y_2}, …, \varphi_{x,y_n}\}.$$
Demostraremos que esta función se acerca muchísimo a $f$ en cualquier punto, específicamente que
Para cada $z \in K, \, \varphi_x(z) \, – \, f(z) < \varepsilon.$
Esto ocurre porque si $z \in K$ entonces existe $j \in \mathbb{N}$ tal que $z \in B(y_j, \delta_{y_j}).$ Así:
\begin{align*}
&& \varphi_x(z) &\leq \varphi_{x,y_j}(z) \\
& \Rightarrow& \varphi_x(z) \, – \, f(z) &\leq \varphi_{x,y_j}(z) \, – \, f(z)
\end{align*}
Y por (3)
\begin{align}
& \Rightarrow& \varphi_x(z) \, – \, f(z) &< \varepsilon
\end{align}
Por el lema 4 de la entrada anterior sabemos que $\varphi_x$ es continua en $x.$ En consecuencia la función $\varphi_x \, – \, f$ también lo es, de modo que existe $\gamma_x >0$ tal que si $z \in B(x, \gamma_{x}),$ entonces por (1) tenemos
\begin{align}
\nonumber |(\varphi_x \, – \, f)(z)\, – \, (\varphi_x \, – \, f)(x)| < \varepsilon\\
\nonumber |(\varphi_x(z) \, – \, f(z))\, – \, \textcolor{blue}{(\varphi_x(x) \, – \, f(x))}| < \varepsilon\\
\nonumber |(\varphi_x(z) \, – \, f(z))\, – \, \textcolor{blue}{0}| < \varepsilon\\
|\varphi_x(z) \, – \, f(z)| < \varepsilon\\
\end{align}
Como $x$ es arbitraria, pensemos ahora en todas las $\varphi_x´s$ que podemos hacer con cada $x \in K.$ Nota que $\{B(x, \delta_{\gamma_{x}})\}_{y \in K}$ es una cubierta abierta de $K$ compacto. Así, existe una subcubierta finita de $ \{B(y, \delta_y)\}_{y \in K},$ es decir, existen
$x_1, \, x_2,…, x_m \in K$ con $m \in \mathbb{N}$ tales que $\{B(x_1, \gamma_{x_1}), \, B(x_2, \gamma_{x_2}),…,B(x_n, \gamma_{x_m})\}$ es una cubierta abierta de $K.$
Sea
$$\hat{\varphi} = \text{máx}\{\varphi_{x_1}, \, \varphi_{x_2}, …, \varphi_{x_m}\}.$$
Como todas las funciones dentro del corchete están en $A,$ también pertenecen a $\overline{A}.$ Por el Lema 4, podemos decir que $\hat{\varphi} \in \overline{A},\, $ (ver tarea moral de esta sección).
A continuación demostraremos que $d_\infty (\hat{\varphi},f) < \varepsilon.$
Sea $z \in K.$
Por un lado, como existe $i \in \{1,2,…,m\}$ tal que $z \in B(x_i, \gamma_{x_i}).$ Sabemos que
\begin{align*}
&&\varphi_x(z) &\geq \varphi_{x_i}(z)\\
&\Rightarrow& \varphi_x(z) \, – \, f(z) &\geq \varphi_{x_i}(z) \, – \, f(z)
\end{align*}
Y por (5)
\begin{align}
\nonumber && \varphi_x(z) \, – \, f(z) &\geq \varphi_{x_i}(z) \, – \, f(z) &> -\varepsilon\\
\nonumber &\Rightarrow& \varphi_x(z) \, – \, f(z) & > -\varepsilon \\
&\Rightarrow& -\varepsilon & < \varphi_x(z) \, – \, f(z)
\end{align}
Como esto ocurre para cualquier $x,$ entonces ocurre para cada $x_k, \, k= 1,2,…,m.$ Se sigue que
\begin{align}
\nonumber && -\varepsilon & < \varphi_{x_k}(z) \, – \, f(z), k= 1,2,…,m\, \\
\nonumber &\Rightarrow& -\varepsilon <& \underset{k \in \{1,…,m\}}{\text{máx}}\{ \varphi_{x_k}(z)\} \, – \, f(z)\\
\nonumber &\Rightarrow& -\varepsilon <& \underset{k \in \{1,…,m\}}{\text{máx}}\{ \varphi_{x_k}(z)\} \, – \, f(z) \\
&\Rightarrow& -\varepsilon <& \hat{\varphi}(z) \, – \, f(z) \\
\end{align}
Por otro lado, en la desigualdad (4) tenemos
\begin{align*}
& \Rightarrow& \varphi_x(z) \, – \, f(z) &< \varepsilon
\end{align*}
Como esto ocurre para cualquier $x,$ entonces ocurre para cada $x_k, \, k= 1,2,…,m.$ Se sigue que
\begin{align}
\nonumber & & \varphi_{x_k}(z) \, – \, f(z) &< \varepsilon, \, k= 1,2,…,m \\
\nonumber & \Rightarrow& \underset{k \in \{1,…,m\}}{\text{máx}}\{ \varphi_{x_k}(z) \, – \, f(z) \} &< \varepsilon \\
\nonumber & \Rightarrow& \underset{k \in \{1,…,m\}}{\text{máx}}\{ \varphi_{x_k}(z)\} \, – \, f(z) &< \varepsilon \\
& \Rightarrow& \hat{\varphi}(z) \, – \, f(z) &< \varepsilon
\end{align}
De (7) y (8) tenemos que para cada $z \in K$
\begin{align}
|\hat{\varphi}(z) \, – \, f(z)| < \varepsilon \\
\end{align}
Y así
\begin{align}
\nonumber &&\underset{z \in K}{sup}|\hat{\varphi}(z) \, – \, f(z)| < \varepsilon \\
&\Rightarrow& d_\infty(\hat{\varphi},f) < \varepsilon
\end{align}
Que es lo que queríamos demostrar.
Finalizamos esta sección con el siguiente:
Corolario. Sea $K \subset \mathbb{R}^n$ compacto y sea $A$ el conjunto de polinomios en $n$ variables que van de $K$ en $\mathbb{R}.$ Entonces toda función continua $f:K \to \mathbb{R}$ se puede aproximar con polinomios, es decir, existe una sucesión de polinomios $(p_n)_{n \in \mathbb{N}}$ tal que $(p_n) \to f$ con la métrica uniforme.
La demostración se deja como ejercicio.
Más adelante…
Complementaremos las ideas de aproximación notando que, para el caso de las funciones continuas en un intervalo cerrado, también es posible encontrar una aproximación a través de lo que llamaremos «función cuadrática por pedazos».
Tarea moral
- Sea $A$ como en las hipótesis del teorema de Stone-Weierstrass. Muestra que si $f_i \in \overline{A}, \, i=1,…,n,$ entonces la función $\underset{i \in \{1,…,n\}}{\text{mín}} \{f_i\}$ también pertenece a $\overline{A}.$
- Prueba el corolario. Sugerencia: Demuestra que satisface las hipótesis del teorema de Stone-Weierstrass. Usa la función proyeccion, que es continua, para probar que cumple d).
- Demuestra que el conjunto de polinomios de grado impar de $[0,1] \to \mathbb{R}$ es denso en $\mathcal{C^0}[0,1].$ ¿Satisface las hipótesis del teorema?
- Sea $f \in \mathcal{C^0}[0,1]$ tal que para cada $n \in \mathbb{N} \cup \{0\}$
$$\int_{0}^{1} f(x)x^ndx=0.$$
Prueba que $\int_{0}^{1} f^2(x)dx=0$ y concluye que $f=0.$