Introducción

En la entrada Contracciones mencionamos el teorema de punto fijo de Banach. Ahí mismo demostramos que si una contracción tiene un punto fijo, entonces este es único. En la entrada anterior vimos que la sucesión generada a partir de una contracción $\phi \,$ y un punto cualquiera $x_0$ del espacio métrico es de Cauchy. Estos dos resultados serán usados a continuación para expresar una demostración del teorema. Recordemos lo que expresa:

Teorema de punto fijo de Banach. Sea $(X,d)$ un espacio métrico completo y sea $\phi:X \to X$ una contracción, entonces:

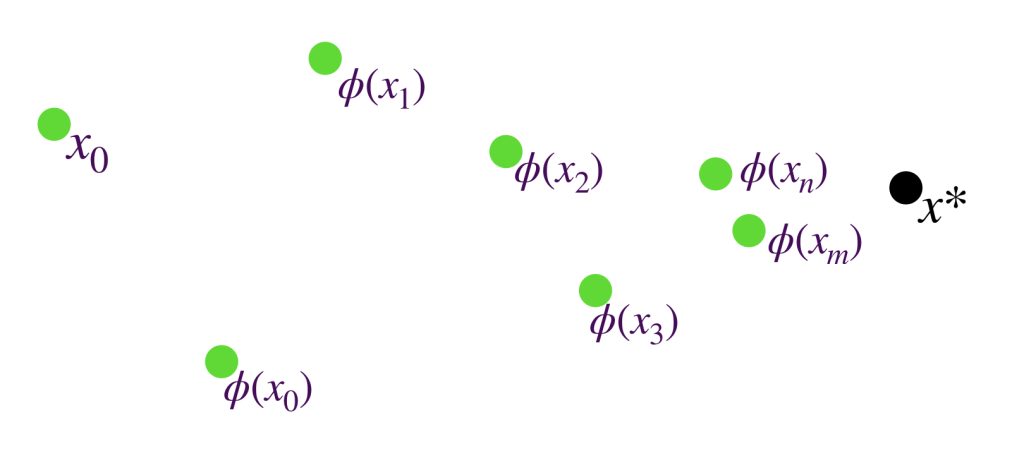
1. Para cada $x_0 \in X$ la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy y, en consecuencia $(\phi^n(x_0))_{n \in \mathbb{N}}$ converge a un punto $x^* \in X.$ $\, \, \phi^n$ representa la composición $\, \underset{n \, veces}{\underbrace{ \phi \circ … \circ \phi }}$
2. El punto $x^*$ descrito es punto fijo de $\phi.$
3. El punto fijo es único.
4. Podemos estimar la distancia de $\phi ^n(x_0)$ a $x^*$ usando la desigualdad:
   $$d( \phi ^n(x_0),x^*) \leq \frac{\alpha^n}{1-\alpha} \, d( x_0,\phi (x_0))$$

Demostración:
1. Se probó en la entrada anterior que la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy. Como aquí agregamos el hecho de que el espacio es completo, concluimos que converge a algún punto $x^* \in X.$

2. Sea $x^* = \underset{n \to \infty}{lim}\, \phi ^n(x_0).$ Probemos que $x^*$ es punto fijo de $\phi.$
Sea $x_n= \phi^n(x_0).$ Apliquemos a cada término la función $\phi$ que como es contracción, entonces es Lipschitz y por tanto es continua, tal como se vio en la entrada Más conceptos de continuidad.

Como
$$(x_n)_{n \in \mathbb {N}} \to x^*$$
se sigue por lo visto en la entrada Funciones continuas en espacios métricos que
$$(\phi(x_n))_{n \in \mathbb {N}} \to \phi(x^*)$$
Pero para cada $n \in \mathbb{N}, \, \phi(x_n)= (x_{n+1})$ de modo que $(\phi(x_n))_{n \in \mathbb {N}}$ es una subsucesión de $(x_n)_{n \to \mathbb {N}} \to x^*.$ En consecuencia $(\phi(x_n))_{n \in \mathbb {N}}$ también converge a $x ^*.$
Pero por la unicidad del límite se sigue que.
$$ \phi(x^*) = x^*$$
Lo cual demuestra que $x^*$ es punto fijo de $\phi.$

3. Se probó en Contracciones.

4. En la demostración vista en la entrada anterior vimos que existe $N \in \mathbb{N}$ tal que si $n,m \geq N$ entonces

$$d(x_n,x_m) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,x_1)$$

Haciendo tender $m \to \infty$ se sigue que

$$d(x_n,x^*) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,x_1)$$

Por lo tanto

$$d(\phi^n(x_0),x^*) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,\phi(x_0)).$$

Que es lo que queríamos demostrar. Nota que esta última desigualdad nos permite acercarnos arbitrariamente al punto fijo de la contracción $\phi$ incluso sin conocerlo, pues su lado derecho puede elegirse tan pequeño como se desee, eligiendo un valor para $n$ suficientemente grande.

Ejemplo. $\phi : \mathbb{C} \to \mathbb{C}, \, \phi(z) = \dfrac{3iz}{4}$

Considera el espacio métrico completo $\mathbb{C}$ con la norma usual. Dejaremos como ejercicio probar que $\phi : \mathbb{C} \to \mathbb{C}, \, \phi(z) = \dfrac{3iz}{4}$ es contracción. La siguiente imagen muestra las primeras iteraciones de $\phi$ partiendo de $x_0 = 1.$ ¿A qué punto converge?

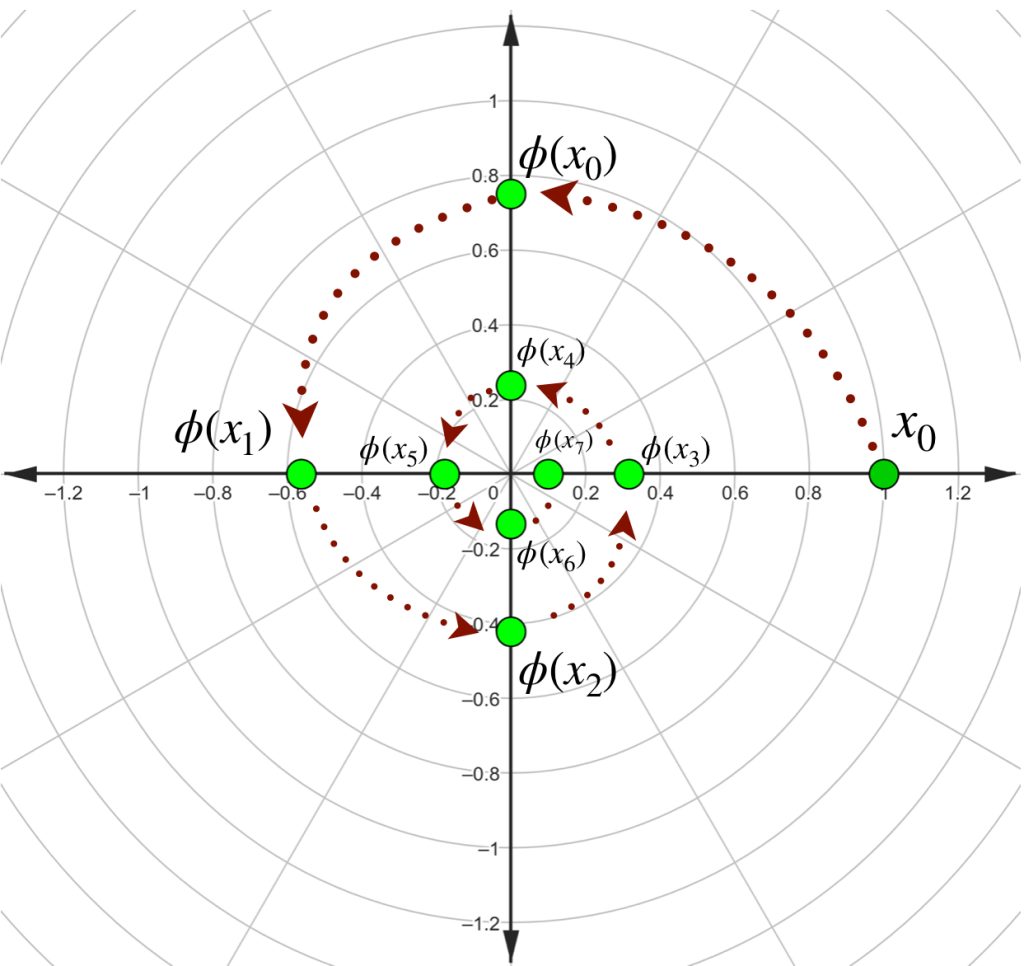
Si $n = 20,$ ¿puedes decir qué tan cerca está $\phi ^n(1)$ del punto fijo? Nota que puedes hacer una estimación sin tener que calcular la norma del punto $\phi ^n(1).$ Da el valor de $N \in \mathbb{N}$ a partir del cual la distancia al punto fijo sea menor que $\dfrac{1}{100}.$

Más adelante

Veremos el teorema de punto fijo de Banach aplicado en la demostración de la existencia y unicidad de la solución de una ecuación diferencial. Esto es, se buscan las funciones que satisfacen cierta ecuación. Estas funciones serán vistas como elementos de un espacio métrico completo. Como llegaremos a que la solución existe y es única, podemos esperar que dicha solución será punto fijo del espacio bajo cierta contracción.

Tarea moral

1. Resuelve las preguntas planteadas en el ejemplo arriba mencionado.
2. Considera el espacio de sucesiones acotadas en $\mathbb{R}$ con norma $\norm{(x_n)_{n \in \mathbb{N}}}= \underset{n \in \mathbb{N}}{sup}\, |x_n|.$
   a) Demuestra que la función $\phi(x_n)_{n \in \mathbb{N}}= (\frac{1}{2}(x_n))_{n \in \mathbb{N}}$ es contracción.
   b) Si $(x_0)$ es la sucesión acotada $(x_{0_n})_{n \in \mathbb{N}}.$ ¿Qué valores de $n \in \mathbb{N}$ satisfacen que la distancia entre $\phi^n(x_0)$ y la sucesión que es el punto fijo de $\phi$ sea menor que $\dfrac{1}{100}?$
3. Sea $X$ un espacio metrico y $\phi:X \to X$ una contracción. Demuestra que:
   a) Para cada $n \in \mathbb{N},$ la función $\phi^n$ es contracción.
   b) Si $x^*$ es punto fijo de $\phi,$ también lo es de $\phi^n.$
   c) Si $\psi: X \to X$ satisface que $\psi \circ \phi = \phi \circ \psi$ entonces $\psi$ tiene un punto fijo.
   d) Si $x^*$ es punto fijo para $\phi^k$ y para $\phi^{k+1}$ para algún $k \geq 2$ entonces $x^*$ es el punto fijo de $\phi.$

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.