$\mathit{\text{ MATERIAL EN REVISIÓN}}$

Introducción

Dedicaremos esta entrada a la presentación de un teorema que ha dado resultados importantes en el estudio de los espacios métricos completos. Para comenzar, necesitamos imaginar la pertenencia de los elementos de un conjunto cuando seleccionamos, arbitrariamente, bolas abiertas en el espacio métrico. El primer concepto dice lo siguiente:

Definición. Conjunto denso. Sean $(X,d)$ un espacio métrico y $A\subset X.$ Decimos que $A$ es un conjunto denso en $X$ si $\bar{A}=X.$

Nota que esto es equivalente a decir que todas las bolas abiertas de $X$ tienen puntos en $A.$

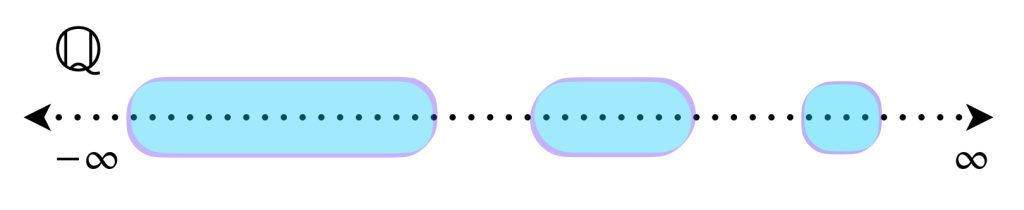
Ejemplo: En el espacio métrico euclidiano de los números reales, el conjunto $\mathbb{Q}$ es denso.

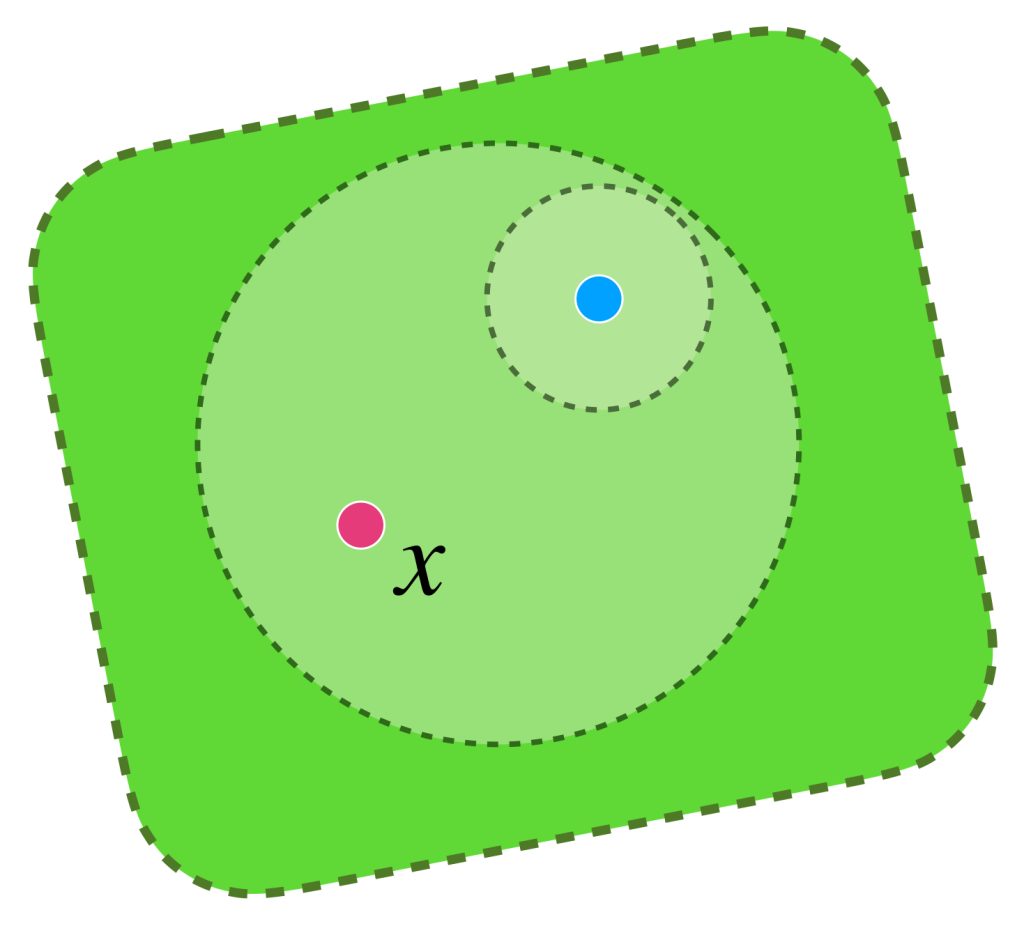
Aunque basta con encontrar una bola abierta en $X$ ajena al conjunto $A$ para demostrar que $A$ no es denso, presentamos un tipo de conjunto que no solo no lo es sino que no lo es en «ninguna parte» de $A.$

Definición. Conjunto nunca denso. Sean $(X,d)$ un espacio métrico y $A\subset X.$ Si para toda bola abierta $B\subset X$ existe una bola abierta contenida $B^{\prime }\subset B$ que no tiene puntos de $A$ diremos que $A$ es un conjunto nunca denso (o denso en ninguna parte).

Con estos conceptos ya podemos entender el teorema prometido.

Teorema de Baire. Si $(X,d)$ es un espacio métrico completo, entonces no puede representarse como la unión numerable de conjuntos nunca densos.

Demostración:
Sea $X$ un espacio métrico completo. Considera el conjunto $\bigcup _{n\in \mathbb{N}}{A}_n,$ donde para cada $n\in \mathbb{N}$ el conjunto $A_n\subset X$ es nunca denso en $X.$ Construiremos una sucesión de bolas cerradas encajadas como sigue: (Concepto visto en entrada anterior).
Sea $B_0$ una bola cerrada de radio $1.$ Como $A_1$ es nunca denso, existe una bola cerrada $B_1$ de radio menor que $\frac{1}{2}$ tal que $B_1\subset B_0$ y $B_1\cap A_1=\mathrm{\varnothing }.$ Proponemos como ejercicio al lector argumentar por qué seleccionar dicha bola es posible.
De igual manera, como $A_2$ es nunca denso existe una bola cerrada $B_2$ de radio menor que $\frac{1}{3}$ tal que $B_2\subset B_1$ y $B_2\cap A_2=\mathrm{\varnothing }.$

Si continuamos recursivamente, terminaremos construyendo una sucesión de bolas cerradas encajadas $(B_n{)}_{n\in \mathbb{N}}$ cuyos radios tienden a $0$. En la entrada anterior vimos que, al ser $X$ completo la intersección de estas bolas tiene un punto, de hecho $\bigcap _{n\in \mathbb{N}}{A}_n=\{x\}$ para algún $x\in X.$ Este punto no pertenece a ningún conjunto $A_k,k\in \mathbb{N},$ pues al estar en la intersección de todas las bolas cerradas, particularmente $x\in B_k$ que, recordemos es ajeno a $A_k,$ por lo tanto $x\notin A_k.$ Entonces tenemos un punto $x\in X$ tal que $x\notin \bigcap _{n\in \mathbb{N}}{A}_n$ concluyendo así que $X\ne \bigcap _{n\in \mathbb{N}}{A}_n.$

A partir de este teorema podemos concluir la siguiente:

Proposición: Todo espacio métrico completo $X$ sin puntos aislados es no numerable.

Demostración:
Recordemos que un punto aislado $x\in X$ es aquel que tiene una bola abierta cuyo único elemento de $X$ es $x.$ Si $X$ no tiene puntos aislados, entonces todos sus puntos son de acumulación. Es sencillo probar que para cada $x\in X$ el conjunto $\{x\}$ es nunca denso (ejercicio).

Si la unión de todos los conjuntos de puntos $\bigcup _{x\in X}\{x\}=X$ fuera numerable tendríamos un espacio completo que contradiga el teorema de Baire. Por lo tanto, si $X$ es completo y sin puntos aislados, entonces es no numerable.

Ejemplo: El espacio euclidiano $\mathbb{R}$ es completo y sin puntos aislados, por lo tanto es no numerable.

El teorema de Baire ha dado resultados fundamentales en el análisis. Los siguientes tres teoremas pueden consultarse en:
Kesavan, S., Functional Analysis (2a ed.). Chennai, India: Editorial Springer, 1996. Pág. 99 y 106.

Teorema de Banach-Steinhaus o de acotación uniforme. Sea $V$ un espacio de Banach y $W$ un espacio lineal normado. Sea $I$ un conjunto indexado para cada $i\in I$ sea $T_i\in \mathcal{L}(V,W).$ Entonces existe $M>0$ tal que

$\Vert T_i\Vert \le M$, para todo $i\in I$

o bien $\underset{i\in I}{sup}\Vert T_i(x)\Vert =\mathrm{\infty }$ para todo $x\in G_{\delta }\subset V.$

Teorema de la función abierta. Sean $V,W$ espacios de Banach y sea $T\in \mathcal{L}(V,W)$ suprayectivo. Entonces $T$ es una función abierta, esto es, si $A\subset V$ es abierto en $V$ entonces $T(A)\subset W$ es abierto en $W.$

Corolario. (También llamado teorema de la función inversa). Sean $V,W$ espacios de Banach y sea $T\in \mathcal{L}(V,W)$ biyectivo, entonces $T$ tiene inversa $T^{-1}$ y esta es continua.

El teorema de la función inversa también es conocido como el teorema de Banach sobre el operador inverso como puede observarse en el problema 3 de Kolmogorov, A.N., Fomin, S.V., Introductory Real Analysis. New York: Dover Publications Inc, 1975. Pág 238. En la página 229 del libro mencionado encontraremos también el:

Teorema Banach: Sea $A$ un operador lineal invertible y acotado que hace un mapeo de un espacio de Banach $E$ en otro espacio de Banach $E_1,$ entonces el operador inverso $A^{-1}$ también es acotado.

También recomendamos visualizar la conferencia
Pichardo, Roberto. «¿Teoría de Conjuntos?, ¡Pero si es bien fácil!». Instituto de Matemáticas de la UNAM. Publicado el 24 de marzo del 2017. YouTube video 59:57
https://www.youtube.com/watch?v=hLFit88zTYk

Roberto Pichardo comienza a describir la Hipótesis del Continuo en el minuto 14 hasta contarnos que esta es equivalente a la igualdad $c:=|\mathbb{R}|={\mathcal{N}}_{\mathcal{1}}.$ El teorema de Baire permite mostrar que

$$\begin{array}{r}{\mathcal{N}}_{\mathcal{1}}\le cov(\mathcal{M})\le c\\ {\mathcal{N}}_{\mathcal{1}}\le non(\mathcal{M})\le c\\ {\mathcal{N}}_{\mathcal{1}}\le add(\mathcal{M})\le c\end{array}$$

Y en consecuencia, esos tres cardinales son iguales.

Más adelante…

Descubriremos que aunque un espacio no sea completo, es posible extenderlo a uno donde sí lo sea. tendremos así la llamada «completación de un espacio métrico.»

Tarea moral

1. ¿Es un conjunto nunca denso un conjunto denso?
2. Da un ejemplo de un conjunto denso que no sea nunca denso.
3. En la demostración del teorema de Baire, argumenta por qué es posible elegir las bolas con el radio indicado.
4. Demuestra que un conjunto $A$ es nunca denso, si y solo si $Int(\bar{A})=\mathrm{\varnothing }.$
5. Prueba que si $x\in X$ con $X$ espacio métrico es un punto de acumulación, entonces $\{x\}$ es nunca denso.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.