Introducción
Como ya se vio, la razón cruzada tiene varias propiedades, desde seis tipos de razón cruzada hasta la construcción del cuarto elemento, pero falta analizar su relación con la circunferencia.
Propiedades de razón cruzada por la circunferencia
Se abordarán 3 propiedades en relación con una circunferencia dada.
Propiedad. Sean cuatro puntos en una circunferencia (con cíclicos) cualesquiera $A,B,C,D$, si unimos estos puntos a dos puntos $O$ y $O’$ que están en la misma circunferencia, entonces los haces $O\{ABCD\}$ y $O’\{ABCD\}$ tienen iguales razones cruzadas.
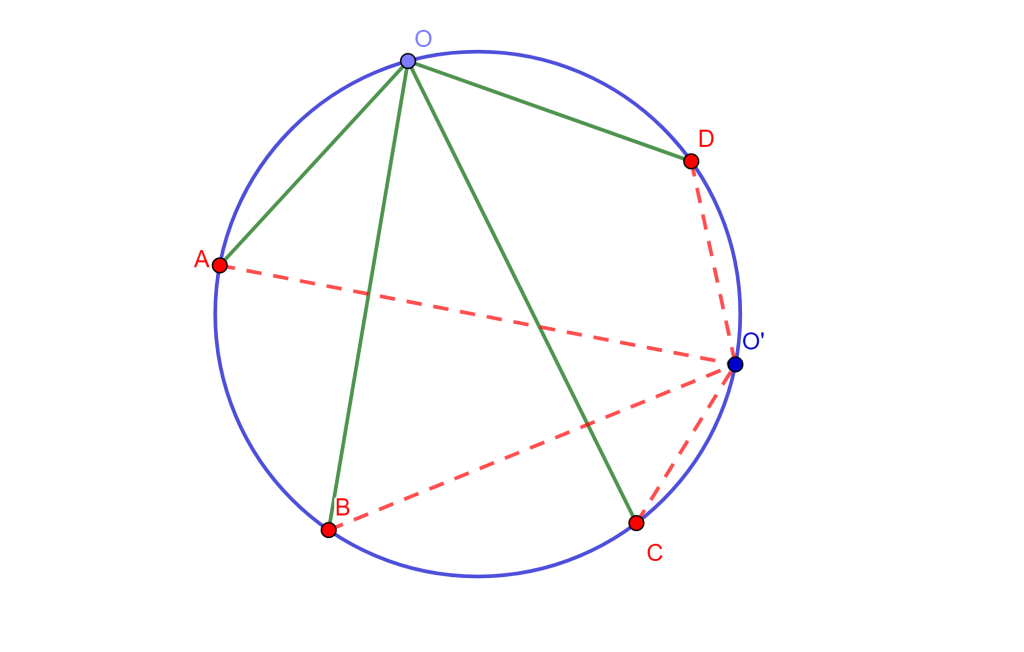
Demostración. Las razones cruzadas son:
$O\{ABCD\}=\frac{sen(AOC)/sen(COB)}{sen(AOD)/sen(DOB)}=k$ y
$O’\{ABCD\}=\frac{sen(AO’C)/sen(CO’B)}{sen(AO’D)/sen(DO’B)}=k’$.
Notemos la igualdad de ángulos correspondientes de los dos haces $\angle{AOC}=\angle{AO’C}$, $\angle{COB}=\angle{CO’B}$, $\angle{DOB}=180-\angle{DO’B}$ y $\angle{AOD}=180-\angle{AO’D}$.
Por lo cual los ángulos formados serán iguales o suplementarios, por ello los senos de los ángulos serán iguales.
$\frac{sen(AOC)/sen(COB)}{sen(AOD)/sen(DOB)}=\frac{sen(AO’C)/sen(CO’B)}{sen(AO’D)/sen(DO’B)}$
$\Rightarrow O\{ABCD\}=k=k’=O’\{ABCD\}.$
$\square$
Propiedad. Sea $C(O,r)$ una circunferencia en la cual se tienen cuatro puntos fijos $A,B,C,D$ por los cuales pasan tangentes por cada uno de estos y cortan la tangente en un punto variable $X$, entonces la razón cruzada de los cuatro puntos de intersección es una constante.
Es decir, $\{A’B’C’D’\}$ es constante independientemente de $X$.
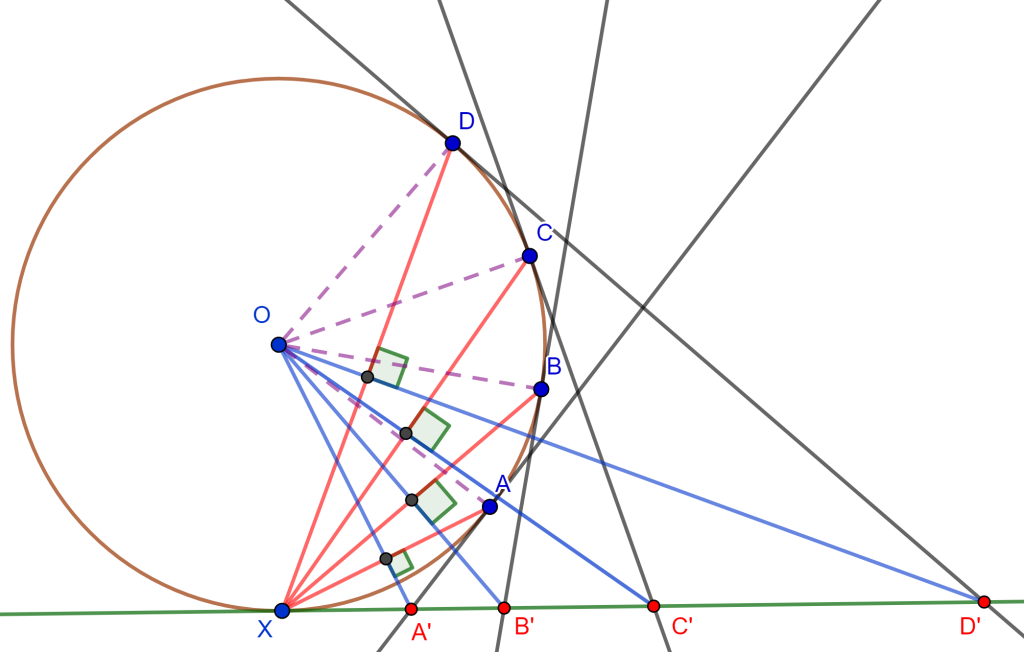
Demostración. Se tiene por teorema visto de razón que $\{A’B’C’D’\}=O\{A’B’C’D’\}$, entonces:
$O\{A’B’C’D’\}=\frac{sen(A’OC’)}{sen(C’OB’)}/\frac{sen(A’OD’)}{sen(D’OB’)}$
Ahora, como los lados correspondientes de los ángulos $C’OB’$ y $CXB$ son perpendiculares, entonces los senos de estos ángulos son iguales, esto ocurre de igual manera para los otros ángulos de los haces $O\{A’B’C’D’\}$ y $X\{ABCD\}$.
$\Rightarrow \frac{sen(A’OC’)}{sen(C’OB’)}/\frac{sen(A’OD’)}{sen(D’OB’)} = \frac{sen(AXC)}{sen(CXB)}/\frac{sen(AXD)}{sen(DXB)} $
$\Rightarrow O\{A’B’C’D’\} =X\{ABCD\}$
Observemos que esto ocurre para cualquier $X’$ entonces $X\{ABCD\}=X’\{ABCD\}$, y por ende se tiene $\{A’B’C’D’\}=O\{A’B’C’D’\}=X’\{ABCD\}$.
Por lo tanto, $\{A’B’C’D’\}=cte$ independientemente de $X$.
$\square$
Propiedad. Sea un haz el cual tiene su vértice fuera de una circunferencia $C(O,r)$ y la cual sus cuatro líneas cortan a la circunferencia en los pares de puntos $A,A’$, $B,B’$, $C,C’$ y $D,D’$. Si se tienen dos puntos distintos $E$ y $E’$ sobre la circunferencia, entonces las razones cruzadas de los haces $E\{ABCD\}$ y $E’\{A’B’C’D’\}$ son iguales.
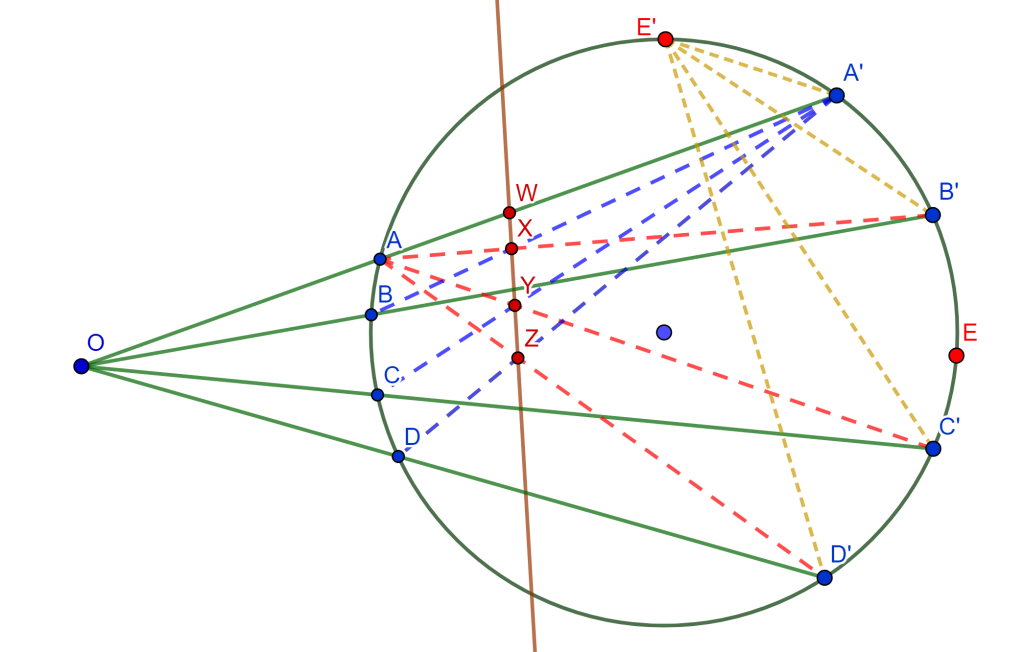
Demostración. Unamos los puntos $A,B,C,D$ a $A’$ y $A’,B’,C’,D’$ a $A$, esto nos dará las intersecciones de $AB’$ y $A’B$ en un punto $X$, $AC’$ y $A’C$ en un punto $y$, $AD’$ y $A’D$ en un punto $Z$, los cuales están en la polar del vértice $O$ del haz dado, por lo cual se tiene por propiedad 1 de razón cruzada en la circunferencia:
$E’\{ABCD\}=E’\{A’B’C’D’\}=A\{A’B’C’D’\}$
Por propiedad de razón cruzada:
$A\{A’B’C’D’\}=\{wxyz\}=A’\{wxyz\}=A’\{ABCD\}$
Y por propiedad 1 de razón cruzada en la circunferencia:
$A’\{ABCD\}=E\{ABCD\}$
Por lo tanto, $E’\{A’B’C’D’\}=E\{ABCD\}$ .
$\square$
Más adelante…
Ahora se abordará el tema de la regla de la falsa proposición y los puntos autocorrespondientes, esto relacionado con la razón cruzada.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Construcción del cuarto elemento dada la razón
- Siguiente entrada del curso: Puntos autocorrespondientes y regla geométrica de la falsa posición
