Introducción

Una vez visto la potencia de un punto P, es hora de analizar una nueva transformación Inversión.

Puntos Inversos con respecto a una circunferencia

Definición. Sea una circunferencia $C(O,r)$ con centro $O$ y radio $r>0$. Si $P$ y $P^{\prime }$ son dos puntos colineales con $O$ se tiene que $P^{\prime }$ es el inverso de $P$ y viceversa si y solo si $P^{\prime }O\times PO=r^2$.

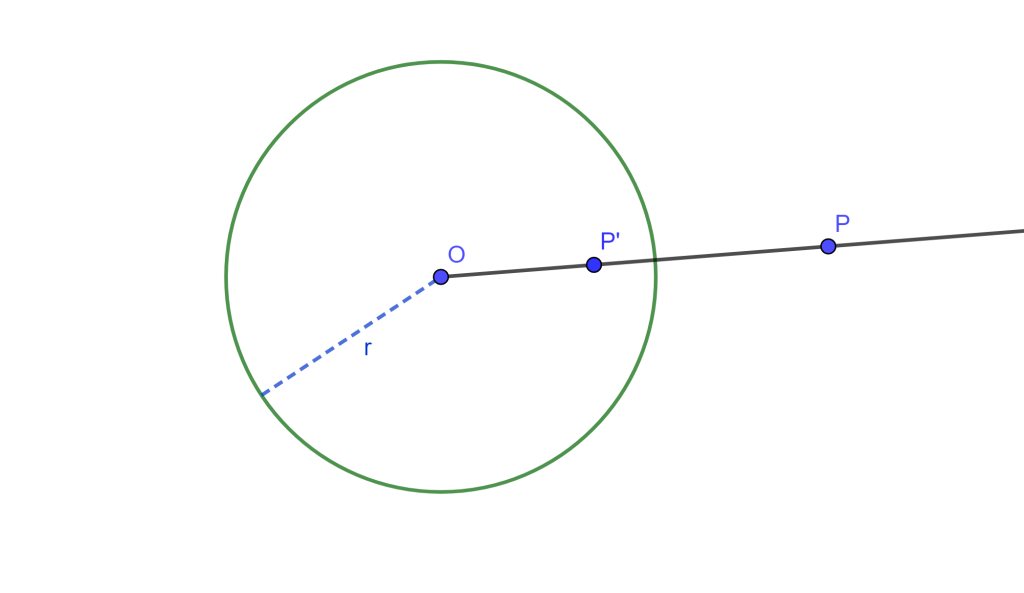
El punto $O$ es el centro de Inversión, la circunferencia $C$ es la circunferencia de inversión, y su radio $»r»$ es el radio de inversión.

Esta es una relación simétrica, ya que $P^{\prime }$ es inverso de $P$ y $P$ es inverso de $P^{\prime }$ con respecto a la circunferencia $C(O,r)$.

Propiedades de Inversión

1. Cada punto en el plano, excepto el centro, tiene un inverso único.
2. El inverso de un punto en la circunferencia de inversión es su propio inverso.
3. El inverso de un punto interior a la circunferencia de inversión es siempre un punto exterior a la circunferencia de inversión.

De esta forma se puede construir el inverso de un punto $P$ con respecto a $C(O,r)$.

Proposición. Sea $C(O,r)$ una circunferencia y un punto $P$, por lo cual existe un $P^{\prime }$ tal que $OP\times O{P}^{\prime }=r^2$.

Demostración. Se considera una circunferencia $C(O,r)$ y un punto $P$, pero existen 3 casos, el punto $P$ interno, externo y sobre la circunferencia $C(O,r)$.

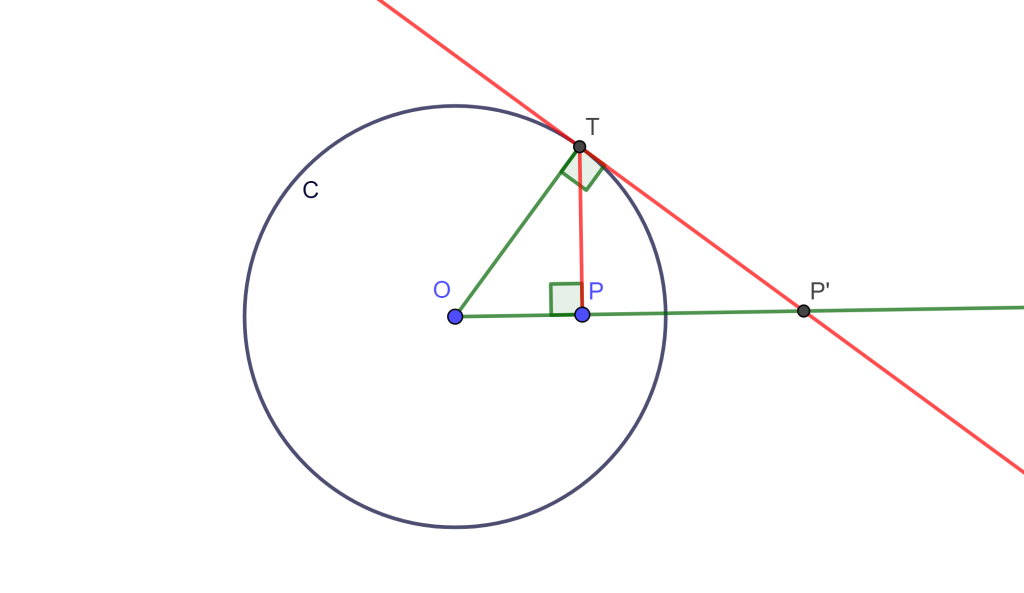
Caso 1. Sea $P$ interno a $C(O,r)$. Trazamos la perpendicular a $OP$ por $P$, donde la intersección es $T$ de la perpendicular a $C(O,r)$. Trazamos $OT$ y trazamos la tangente a $C(O,r)$ por $T$, llamemos $P^{\prime }$ a la intersección de $OP$ con respecto a la tangente mencionada.

Por construcción $\mathrm{\angle }OT{P}^{\prime }=\pi /2=\mathrm{\angle }OPT$, y los triangulos $\mathrm{△}OTP$ y $\mathrm{△}O{P}^{\prime }T$ comparten $\mathrm{\angle }O$, por lo cual son semejantes, entonces $\mathrm{△}OTP\approx \mathrm{△}O{P}^{\prime }T$.

$\Rightarrow \frac{O{P}^{\prime }}{OT}=\frac{OT}{OP}\iff OP\times O{P}^{\prime }=r^2$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

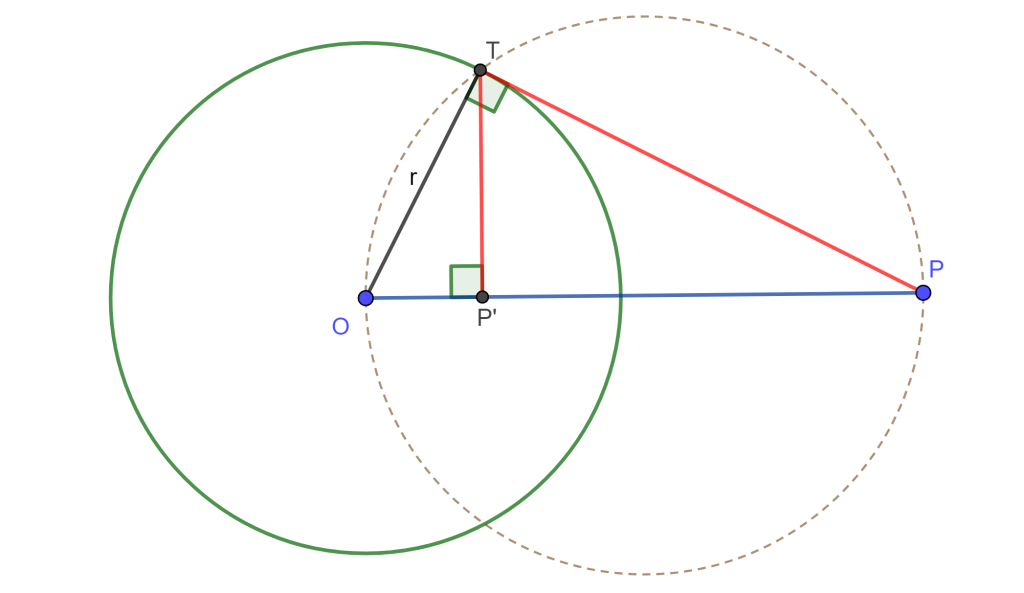
Caso 2. Sea $P$ externo a $C(O,r)$. Trazamos una circunferencia de diámetro $PO$ y unimos $P$ con la intersección de las 2 circunferencias, la cual llamaremos $T$.
De $T$ sacamos la perpendicular respecto a $OP$, la intersección será $P^{\prime }$.

El angulo $\mathrm{\angle }OTP=\pi /2$ ya que abarca el diametro $OP$. Ahora los $\mathrm{△}O{P}^{\prime }T\approx \mathrm{△}OTP$ porque comparten $\mathrm{\angle }TOP$ y $\mathrm{\angle }OTP=\pi /2=\mathrm{\angle }O{P}^{\prime }T$

$\Rightarrow \frac{O{P}^{\prime }}{OT}=\frac{OT}{OP}\iff O{P}^{\prime }\times OP=OT\times OT=r^2$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

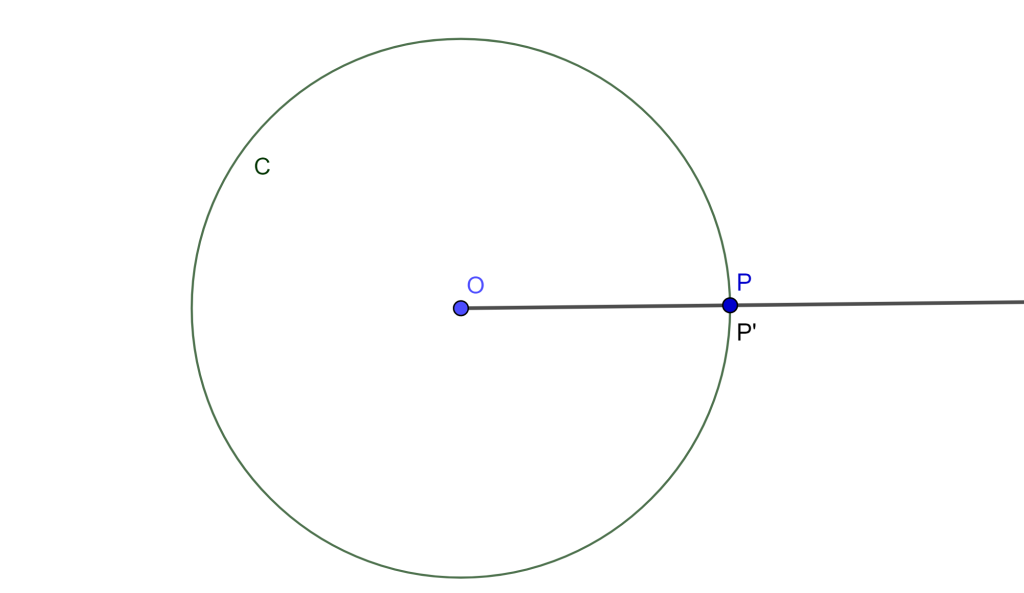
Caso 3. Sea $P$ está en $C(O,r)$. Su inverso $P^{\prime }$ con respecto a $C(O,r)$ es colineal con $P$ y $O$, y además $OP=r$ entonces se debe cumplir $OP\times O{P}^{\prime }=r^2$

$\Rightarrow r\times O{P}^{\prime }=r^2\Rightarrow O{P}^{\prime }=r\Rightarrow O{P}^{\prime }=OP\Rightarrow P^{\prime }=P$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Ahora veremos un teorema que será útil más adelante.

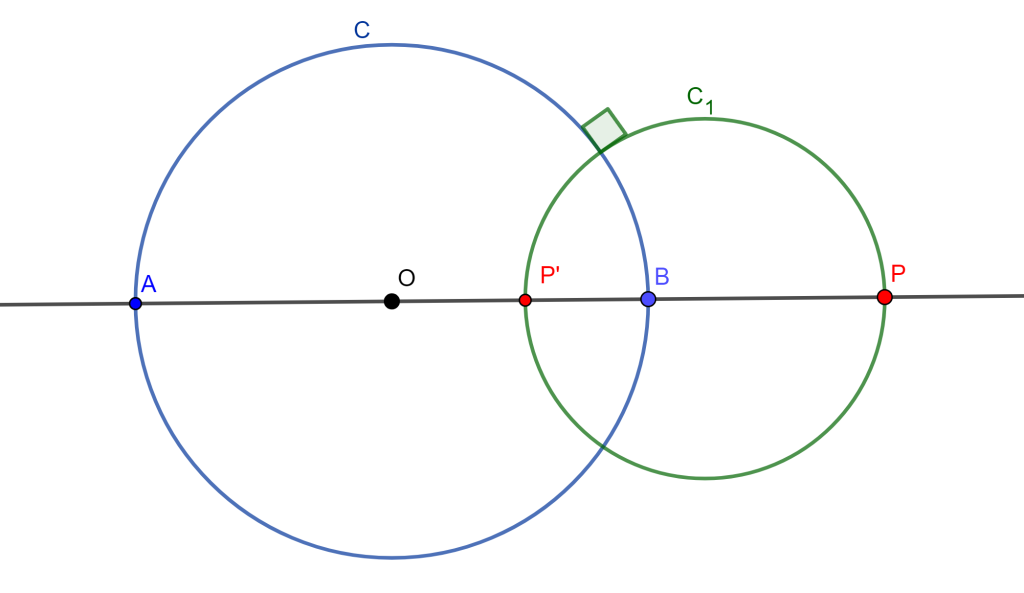
Teorema. Sea $C(O,r)$ una circunferencia de inversión, $P$ y $P^{\prime }$ dos puntos inversos respecto a $C$. Cualquier circunferencia que pase por $P$ y $P^{\prime }$ es ortogonal a $C$.

Demostración. Sea $C$ una circunferencia y $OP$ un segmento, sean $A$ y $B$ los puntos donde $OP$ toca a $C$ y $B\in OP$

Por hipótesis $OP\times O{P}^{\prime }=r^2$ y $O$ es punto medio de $AB$
$\Rightarrow P^{\prime }$ y $P$ son armónicos respecto a $A$ y $B$
$\Rightarrow (\frac{A{P}^{\prime }}{P^{\prime }B})=-(\frac{AP}{PB})$
Ahora como $C$ pasa por $A$ y $B$, y $C_1$ pasa por $P^{\prime }$ y $P$ entonces $C\perp C_1$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más adelante

Una vez ya estudiado la definición de inversión y sus propiedades, es momento de analizar como afecta la inversión a otros objetos geométricos, en específico en Rectas y Circunferencias.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Ejercicios Unidad 1
• Siguiente entrada del curso: Inversión de Rectas y Circunferencias