Archivo de la etiqueta: órbita de un elemento

Álgebra Moderna I: Tamaño de una órbita y de un estabilizador

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En esta entrada repasaremos lo que vimos en la entrada anterior. Primero, veremos unos ejemplos que ilustran las definiciones de órbita y estabilizadores. A partir de estos ejemplos podremos observar ciertos patrones que se repiten y los analizaremos formalmente en una proposición. Por último, daremos un último ejemplo para ilustrar dicha proposición.

Ejemplos de Acciones

Repasemos lo que hemos visto con los siguientes ejemplos. En cada ejemplo describimos el grupo $G$, la órbita y los estabilizadores de los elementos.

Ejemplo 1. Consideremos la permutación $\alpha = (1\,2\,3\,4) \in S_6$. Sean $G = \left<\alpha\right>$ y $X = \{1,2,3,4,5,6\}$ con la acción dada por $\alpha^k \cdot i = \alpha^k(i)$ para toda $k\in \z, i\in X.$

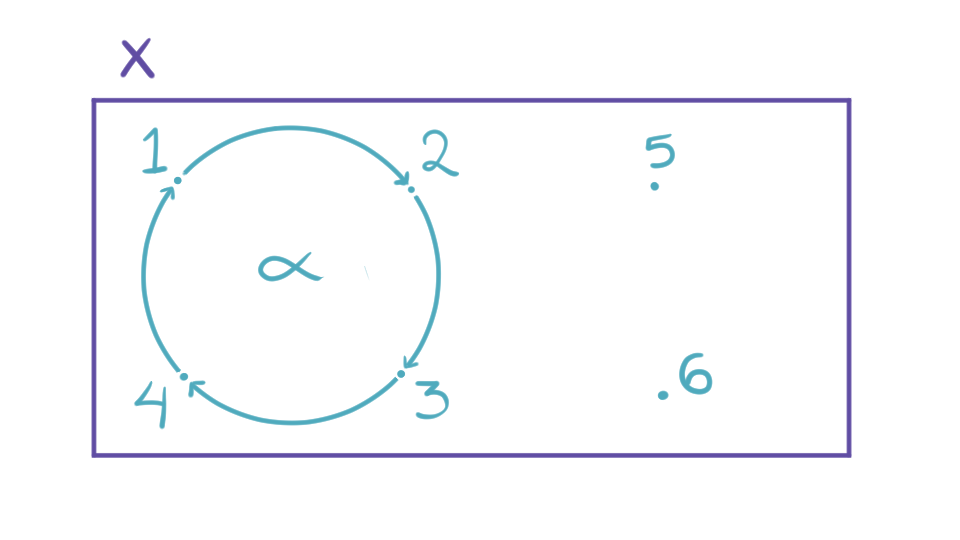
Este diagrama nos ayuda a entender cómo funciona $\alpha$ y qué sucede cuando aplicamos $\alpha^2$, $\alpha^3$, $\dots$. Los elementos del círculo van cambiando en el orden indicado por las flechas.
Además, $\alpha$ deja fijos al 5 y al 6.

Comencemos describiendo a las órbitas de los elementos:
\begin{align*}
\mathcal{O}(1) &= \{1,2,3,4\}\\
&= \mathcal{O}(2) = \mathcal{O}(3) = \mathcal{O}(4)\\
\mathcal{O}(5) &= \{5\}\\
\mathcal{O}(6) &= \{6\}.
\end{align*}

Observemos que las órbitas de $1, 2, 3$ y $4$ son iguales porque $\alpha$ es una permutación cíclica que mueve esos elementos, pero como $\alpha$ deja fijos a $5$ y a $6,$ sus órbitas son distintas y consisten solamente de sí mismos.

Ahora, podemos describir mejor a $G = \left< \alpha \right>$. Como $\alpha$ tiene orden 4, $G$ quedaría:

$$G = \{(1), \alpha, \alpha^2,\alpha^3\}.$$

Por último, describamos los estabilizadores. De acuerdo a la definición de la entrada previa el estabilizador de un objeto son los elementos del grupo que fijan al objeto, en este caso las potencias de $\alpha$ que dejan fijo al objeto. En el caso del $1$ la única potencia de $\alpha$ que lo fija es la identidad y análogamente para $2,3$ y $4$. Por otro lado en el caso de $5$ y $6$, como $\alpha$ no los mueve en absoluto, cualquier potencia de $\alpha$ forma parte de sus respectivos estabilizadores. Esto quedaría escrito de la siguiente manera:
\begin{align*}
G_1 &= \{\alpha^k \in G | \alpha^k \cdot 1 = 1\} = \{(1)\}\\
&= G_2 = G_3 = G_4. \\\\
G_5 &= \{\alpha^k \in G | \alpha^k \cdot 5 = 5\} = G = \{(1), \alpha, \alpha^2,\alpha^3\} \\&= \{\alpha^k \in G | \alpha^k \cdot 6 = 6\}= G_6.
\end{align*}

Ejemplo 2. Consideremos ahora la permutación $\beta = (1\,2\,3)(4\,5)\in S_5$. Sean $G = \left< \beta \right>$ y $X= \{1,2,3,4,5\}$ con la acción dada por $\beta^k \cdot i = \beta^k(i)$ para todas $k\in\z$ y $i\in X.$

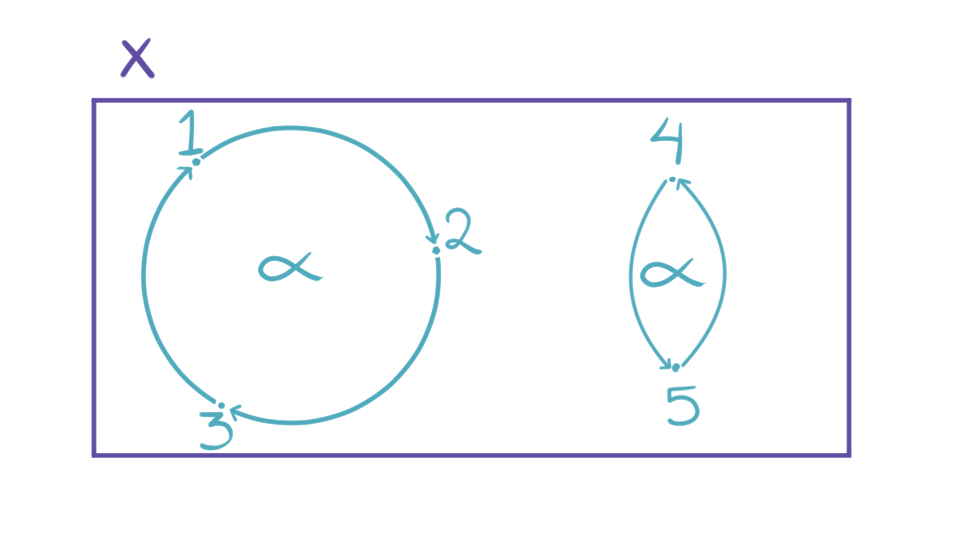
Este diagrama ilustra el efecto de $\beta$ en los elementos de $X$. Podemos ver como $1, 2$ y $3$ forman un ciclo y, $4$ y $5$ forman otro.

Primero, describamos las órbitas de los elementos:

\begin{align*}
\mathcal{O}(1) &= \{1,2,3\} = \mathcal{O}(2) = \mathcal{O}(3).\\
\mathcal{O}(4) &= \{4,5\} = \mathcal{O}(5).
\end{align*}

Ahora, describamos mejor a $G$. Observemos que $\beta$ está compuesta por dos ciclos disjuntos: $(1\, 2\, 3)$ con orden $3$ y $(4\,5)$ con orden $2$, es decir es el producto de dos ciclos que conmutan y que tienen órdenes primos relativos entre sí. Por el último teorema de la entrada Palabras, el orden de $\beta$ es entonces $6$. Así, $G$ quedaría descrito como:
$$G = \{(1), \beta, \beta^2, \beta^3, \beta^4,\beta^5\}.$$

Por último, describamos los estabilizadores de cada elemento.

\begin{align*}
G_1 &= \{\beta^k \in G | \beta^k(1) = 1\} = \{(1),\beta^3\}\\
&= G_2 = G_3. \\\\
G_4 &= \{\beta^k\in G | \beta^k(4) = 4\} = \{(1), \beta^2, \beta^4\}\\
&= \{\beta^k\in G | \beta^k(5) = 5\} = G_5.
\end{align*}

Antes de avanzar a la siguiente sección, considera los ejemplos estudiados e intenta determinar si existe alguna relación entre $\#\mathcal{O}(x)$, $|G_x|$ y $|G|$.

¿Qué relación existe entre el tamaño de la órbita y el tamaño del estabilizador de un elemento?

Los ejemplos que trabajamos al inicio de esta entrada nos pueden dar la idea de que existe algún tipo de relación entre los tamaños de la órbita y del estabilizador para cada elemento.

Proposición. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$.
\begin{align*}
\#\mathcal{O}(x) = [ G:G_x].
\end{align*}

Demostración.

Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. Dado que $[ G:G_x]=\# \{gG_x| g\in G\}$ bastaría con encontrar una biyección entre $\mathcal{O}(x)$ y $\{gG_x| g\in G\}.$
Proponemos $\varphi : \mathcal{O}(x) \to \{gG_x| g\in G\}$ tal que $g\cdot x \mapsto gG_x$ para todo $g\in G.$

Debemos probar que $\varphi$ es una biyección.

Primero, veamos que está bien definida. Tomemos $g,h\in G$, y supongamos que $g\cdot x = h\cdot x$.

Entonces

Esto implica,
\begin{align}\label{ec1}
h^{-1}\cdot (g\cdot x) &= h^{-1}\cdot (h\cdot x)
\end{align}

Por las propiedades de acción, al desarrollar la parte derecha de la igualdad \ref{ec1} obtenemos
\begin{align*}
h^{-1}\cdot (h\cdot x) &= (h^{-1}h)\cdot x\\
&= e\cdot x = x.
\end{align*}

Por otro lado al desarrollar la parte izquierda de la igualdad \ref{ec1} obtenemos que,
\begin{align*}
h^{-1}\cdot(g\cdot x) = (h^{-1}g)\cdot x,
\end{align*}

así, $ (h^{-1}g)\cdot x=x$ y esto por definición quiere decir que $h^{-1}g\in G_x$.
Por lo que estudiamos en clases laterales, esto implica que $gG_x = hG_x$, es decir que $\varphi(g\cdot x)=\varphi(h\cdot x)$.
Así, concluimos que $\varphi$ está bien definida.

Ahora, probaremos que $\varphi$ es unyectiva.
Sean $g, h \in G$, tales que $\varphi(g\cdot x) = \varphi(h\cdot x)$, es decir tales que $g G_x = hG_x.$ Pero
\begin{align*}
g G_x &= hG_x\\
\Rightarrow &h^{-1} g\in G_x &\text{Por lo que sabemos de clases laterales}\\
\Rightarrow &(h^{-1}g)\cdot x = x & \text{Por estar en el estabilizador}\\
\Rightarrow &h\cdot ((h^{-1}g)\cdot x) = h\cdot x. &\text{Haciendo actuar $h$}\\ \Rightarrow &g\cdot x=((hh^{-1})g)\cdot x =(h(h^{-1}g))\cdot x =h\cdot ((h^{-1}g)\cdot x) = h\cdot x. &\text{Por las propiedades de acción.}\\
\end{align*}

Así $\varphi$ es inyectiva.

Por construcción podemos observar que $\varphi$ es suprayectiva.

Por lo tanto $\#\mathcal{O} = [ G:G_x]$.

$\blacksquare$

Como consecuencia de lo anterior obtenemos el siguiente corolario.

Corolario. Sea $G$ un grupo finito, $X$ un $G$-conjunto, $x\in X.$ Entonces, $\# \mathcal{O}(x)$ divide a $|G|.$

Ejemplo del Dodecaedro

Veamos un ejemplo en el que apliquemos lo que acabamos de ver.

Consideremos el dodecaedro $D$.

Si pensamos en todas las simetrías en $\r^3$ que mandan el dodecaedro en sí mismo, podemos tomar las rotaciones y así definir $G = \{\varphi \text{ rotación en }\r^3 | \varphi[D]= D\}$.

¿Cuál es el orden de $G$?

Sea $X$ el conjunto de caras de $D$, $G$ actúa en $X$ ya que manda caras de $D$ en caras de $D$. La acción es transitiva ya que cada cara se puede llevar a cualquier cara contigua mediante una rotación de $\displaystyle\frac{2\pi}{3}.$

Si el eje de rotación va del origen a un vértice, las caras rotarán tomando el lugar de otras caras. En cambio, si el eje de rotación cruza del origen al centro de una cara, esa cara rotará sobre sí misma y cada que rote $\displaystyle r = \frac{2\pi}{5}$ seguirá en su lugar.

Rotación de $\frac{2\pi}{5}$ del dodecaedro cuando el eje pasa por el centro de una cara. Las caras superiores e inferiores rotan sobre sí mismo.
Rotación de $\frac{2\pi}{3}$ del dodecaedro cuando el eje pasa por un vértice.

Así, dado $x\in X$, habrá exactamente cinco rotaciones que mandan la cara $x$ en sí misma (aquellas rotaciones de ángulo $ \frac{2\pi}{5}$ cuyo eje de rotación cruza del origen al centro de una cara), por lo cual $|G_x| = 5$. Además, como la acción es transitiva $\# X = \#\mathcal{O}(x)$. Luego, $\#X = 12$ y $\#\mathcal{O}(x) = [G:G_x ]$. Pero $\displaystyle [G:G_x ] = \frac{|G|}{5}$. Si juntamos todo eso, obtenemos:
$$12 = \# X = \#\mathcal{O}(x) = [G:G_x ]= \frac{|G|}{5}.$$

Despejando, $|G| = 12\cdot 5 = 60.$ Es decir, tenemos 60 rotaciones en $\r^3$ que son simetrías del dodecaedro.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $G$ un grupo finito actuando sobre sí mismo:
    • Determina si el hecho de que exista $x\in G$ y tal que $G_x =\{e\}$ implica que la acción es transitiva.
    • Determina si el hecho de que la acción sea transitiva implica que exista $x\in G$ tal que $G_x =\{e\}$.
  2. Encuentra el orden del grupo de simetrías de cada sólido platónico (recuerda que hay algunos que son duales y por lo tanto tienen el mismo grupo de simetrías).

Más adelante…

Ya casi acabamos de estudiar la órbita, todavía nos queda analizar con ás detalle el caso cuando $X=G$, es decir cuando $G$ actúa sobre sí mismo. También podemos preguntarnos qué sucede con el conjunto de elementos de $X$ que se quedan fijos ante cualquier elemento de $G$ que actúe sobre ellos. Esto nos servirá para llegar a una importante ecuación llamada la ecuación de clase.

Además, en la siguiente entrada definiremos un nuevo tipo de grupo conocido como $p$-grupo y esto nos perfilará para llegar a los Teoremas de Sylow.

Entradas relacionadas

Álgebra Moderna I: Órbita de $x$ y tipos de acciones

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Tomemos un grupo $G$ y $X$ un $G$-conjunto. A lo largo de esta entrada consideraremos la relación de equivalencia en $X$ inducida por esta acción y que fue definida en la entrada anterior de la siguiente manera:

$x\sim y$ si y sólo si $g\cdot x = y$ para algún $g\in G$.

Continuemos entonces con esta idea, comenzando por definir las clases de equivalencia inducidas por esa relación.

Después, definiremos nuevos tipos de acciones, por ejemplo, ¿qué pasa si la relación sólo induce una clase de equivalencia? o ¿qué sucede con el conjunto de objetos que dejan fijo a los elementos de $G$?

Órbita de un elemento de $X$

Dada la importancia de esta manera de relacionar a los elementos de un grupo de acuerdo a una acción, daremos un nombre a sus clases de equivalencia.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Para cada $x\in X$, la órbita de $x$ es
\begin{align*}
\mathcal{O}(x) = \{g\cdot x | g \in G\},
\end{align*}

es decir, todos los objetos que podemos obtener haciendo actuar a $G$ sobre $x$.

Observación. Sean $G$ un grupo, $X$ un $G$-conjunto. Tenemos que $\mathcal{O}(x)$ es la clase de equivalencia de $x$ con respecto a la relación inducida por la acción de $G$ en $X$.

Demostración.

Sea $x\in G$. Sabemos que la clase de equivalencia de $x$, denotada por $[x]$, se define como:
\begin{align*}
[ x ] &= \{y\in X |x\sim y\} &\text{Definición de clase de equivalencia} \\
&= \{y\in X|\exists g\in G \text{ con }g\cdot x = y\} &\text{Definición de la relación }\sim\\
&= \{g\cdot x| g\in G\} = \mathcal{O}(x) &\text{Definición de órbita.}
\end{align*}

$\blacksquare$

De cursos anteriores sabemos que la colección de clases de equivalencia inducidas por una relación es una partición del conjunto. El siguiente teorema se da como consecuencia de las propiedades de una partición.

Teorema. Sean $G$ un grupo, $X$ un $G$-conjunto. Entonces

  1. $\mathcal{O}(x) \neq \emptyset $ para toda $x\in X$.
  2. Sean $x,y\in X$. Si $\mathcal{O}(x)\cap \mathcal{O}(y)\neq \emptyset$, entonces $\mathcal{O}(x) = \mathcal{O}(y)$.
  3. $\displaystyle X = \bigcup_{x\in X}\mathcal{O}(x)$.

Este teorema sólo enlista las propiedades de una partición en el caso particular en el que estamos trabajando, por lo que no hay nada nuevo que demostrar.

Una acción transitiva

Las órbitas están determinadas por varios factores: el conjunto $X$, el grupo $G$ y la acción de $G$ en $X$. En algunos casos existe una única órbita.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Si $\mathcal{O}(x) = X$ para alguna $x\in X$, decimos que la acción es transitiva.

Esta definición nos dice que podemos obtener cualesquier elemento de $X$ haciendo actuar algún elemento del grupo en el objeto $x$.

Ejemplos de acciones transitivas

Ejemplo 1. Dado $G$ un grupo, $X=G$ definimos la acción de $G$ en sí mismo mediante la operación de $G$, es decir $a\cdot x = a x$ para todas $a\in G$, $x\in X.$

Consideremos cualquier $x\in X$. Sea $y\in X$. Siempre tenemos una manera de obtener $y$ a través de $x$:
\begin{align*}
y = y(x^{-1}x) = (yx^{-1})x = (yx^{-1})\cdot &x \in \mathcal{O}(x). \\
\text{Entonces } &y \in \mathcal{O}(x).
\end{align*}

Por lo tanto $\mathcal{O}(x) = X$ y así la acción es transitiva.

Ejemplo 2. Sean $G$ un grupo, $H\leq G$, $X = \{gH | g\in G\}$. Definimos $a\cdot (gH) = agH$ para todas $a,g\in G.$

Consideremos cualquier $gH \in X.$ Sea $tH \in X$ con $t\in G.$ Podemos reescribir al representante como:
\begin{align*}
t H &= t(g^{-1}g) H = (tg^{-1})gH \\
&= (tg^{-1})\cdot gH \in \mathcal{O}(gH).
\end{align*}

Por lo tanto $\mathcal{O}(gH) = X$. Así, la acción es transitiva.

Ejemplo 3. Sea $G = D_{2(n)}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices del polígono regular de $n$ lados.

La acción que ya habíamos trabajado: dados $g\in G$, $i\in X$ definimos $g\cdot i = g(i)$.

Dada $a\in G$ la rotación $\displaystyle\frac{2\pi}{n}$ y $1\in X$, tenemos que
\begin{align*}
\text{id}\cdot 1 &= 1, \\
a\cdot 1 = a(1) &= 2,\\
a^2 \cdot 1 = a^2(1) &= 3, \\
&\vdots \\
a^{n-1} \cdot 1 = a^{n-1} (1) &= n.
\end{align*}

Entonces $X = \{1,2,\cdots,n\}\subseteq \mathcal{O}(1) \subseteq X$. Así, $\mathcal{O}(1) = X$. Por lo tanto la acción es transitiva.

Ejemplo 4. Ahora veamos un ejemplo nuevo.

Sea $G$ un grupo, $X= G$. Dados $a\in G$, $x\in X$ definimos
\begin{align*}
a\cdot x &= a x a^{-1}.
\end{align*}

Demostremos que es una acción:
\begin{align*}
e\cdot x &= exe^{-1} = x &\forall x\in X.\\
a\cdot(b\cdot x) &= a(b\cdot x)a^{-1} = a(bxb^{-1})a^{-1} = (ab)x(ab)^{-1}& \text{Asociando diferente}\\
&= (ab)\cdot x &\forall a,b\in G, \forall x\in X.
\end{align*}

Así, $G$ actúa en sí mismo por conjugación.

Dado $x\in X$,
\begin{align*}
\mathcal{O}(x) = \{g\cdot x | g\in G\} = \{gxg^{-1}| g\in G\}
\end{align*}
que son todos los conjugados de $x$.

En este caso, la acción no siempre es transitiva: Si $ G\neq \{e\}$ consideremos $x\in G\setminus\{e\}.$ Si $e\in \mathcal{O}(x)$ entonces $e = g\cdot x = gxg^{-1}$ para algún $g\in G$ y entonces $e = x$, esto es una contradicción porque $x\in G\setminus\{e\}$. Así, $\mathcal{O}(x)\neq X$ y la acción no es transitiva.

Más definiciones de acciones

En toda acción el neutro del grupo actúa de forma trivial en todos los elementos del conjunto pero puede ser que existan otros elementos del grupo con esa propiedad. Si no es el caso decimos que la acción es fiel:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto. Decimos que la acción es fiel si $g\cdot x = x$, con $g\in G$, para todo $x\in X$, implica que $g=e.$

Consideremos ahora los elementos del grupo que fijan a algún elemento específico del conjunto:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. El estabilizador de $x$ es
\begin{align*}
G_x = \{g\in G | g\cdot x = x\}.
\end{align*}

Es decir, la colección de todos los elementos de $G$ que dejan fijo a $x$.

Ejemplos de acción fiel y estabilizador

Ejemplo 1. Sea $G$ un grupo, $X = G$ y $g\cdot x = gx$ para todo $g,x \in G.$

Si $g\in G$ es tal que $g\cdot x = x$ para toda $x\in X$, entonces $gx = x$ para toda $x\in X$, en particular $g = ge = e.$

Así $g=e$ y la acción es fiel.

Dado $x\in X$,
\begin{align*}
G_x = \{g\in G | g\cdot x = x\} = \{g\in X| gx = x\}.
\end{align*}

Pero si $gx = x$,por cancelación $g=e$. Así $G_x = \{e\}$ para toda $x\in X,$ de modo que los estabilizadores son triviales.

Ejemplo 2. Sean $G$ grupo, $H$ subgrupo de $G$, $X = \{xH | x\in G\}$ con $g\cdot(xH) = gx H$ para toda $g,x\in G.$

Si $g\in G$ es tal que $g\cdot (xH) = xH$ para toda $x\in G$, entonces
\begin{align*}
gxH &= xH &\forall x\in G\\
\Rightarrow \, x^{-1} g x &\in H & \forall x\in G\\
\Rightarrow \, g&\in xHx^{-1} & \forall x\in G.
\end{align*}

Si $H\unlhd G$ esto se cumple para toda $g\in H$. Por lo tanto la acción no necesariamente es fiel.

Ahora, dada una clase lateral $xH \in X$.
\begin{align*}
G_{xH} &= \{g\in G | g\cdot (xH) = xH\}\\
&= \{g\in G| gxH = xH\}\\
&= \{g\in G | x^{-1}gx\in H\} \\
&= \{g\in G | g\in xHx^{-1}\}\\
&= xHx^{-1}.
\end{align*}

Así $G_{xH} = xHx^{-1}$ para toda $x\in G.$

Ejemplo 3. Sean $G = D_{2(n)}$ el grupo diédrico, $X = \{1,2,\cdots, n\}$ los distintos vértices del polígono regular de $n$ lados.

Dados $g\in G, i \in X$ definimos $g\cdot i = g(i)$.

Si $g\in G$ es tal que $g\cdot i = i$ para toda $i \in X$, entonces $g(i) = i$ para toda $i\in X$. Así, $g$ sería una transformación lineal en el plano, que fija a los vértices $1$ y $2,$ los cuales forman una base del plano. Por lo tanto $g = \text{id}$ y la acción es fiel.

Dado $i\in X$,
\begin{align*}
G_i &= \{g \in G | g\cdot i = i\}\\
&= \{g\in G | g(i) = i\}\\
&= \{\text{id},r_i\}
\end{align*}
con $r_i$ la reflexión con respecto a la recta que pasa por $(0,0)$ y $i.$

Por último, veremos una observación.

Ilustración de lo que sucede con $r_i$ de $D_{2(n)}.$ Usamos $D_{2(4)}$ representado con un cuadrado y $D_{2(8)}$ representado con un octágono. En el dibujo, $r_1$ mantiene fijo a 1 y 3, y $r_3$ mantiene fijo a 3 y 7.

Observación. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. $G_x$ es un subgrupo de $G$.

Demostración.
Sean $G$ grupo, $X$ un $G$-conjunto, $x\in X.$

El neutro de $G$ siempre está en el estabilizador porque:
\begin{align*}
e\cdot x = x \quad \forall x\in X,
\end{align*}

entonces $e\in G_x.$

Si $a,b\in G_x$, entonces $(ab)\cdot x = a\cdot (b\cdot x) = a\cdot x = x = x$. Así, $ab\in G_x$. Es decir, el estabilizador es cerrado bajo producto.

Finalmente si $a\in G_x$, $a\cdot x = x$, entonces $a^{-1}\cdot x = a^{-1}\cdot (a\cdot x) = (a^{-1}a)\cdot x = e\cdot x = x$, así $a^{-1} \in G_x$.

Por lo tanto $G_x \leq G$.

$\blacksquare$

Tarea moral

  1. En cada uno de los incisos del ejercicio 1 de la entrada de acciones, en donde haya una acción, describe cómo son las órbitas y determina si se trata de una acción transitiva.
  2. Considera el conjunto $X = \{1,2,3,4,5,6,7,8\}$ y el grupo $G = \left< a \right>$ con $a\in S_8$. Define $a^{i}\cdot j = a^{i}(j)$ para cada $a^{i} \in G$ y cada $j\in X$.
    • Verifica que es una acción de $G$ en $X$.
    • Si $a = (2 \; 4 \; 1 \; 7 \; 8)$ describe las órbitas y determina si se trata de una acción transitiva.
    • Si $a = (6 \; 1 \; 5 \; 8)(3 \; 4)$ describe órbitas y determina si se trata de una acción transitiva.
  3. Sea $G$ un grupo y $X$ un $G$-conjunto. Si la acción de transitiva prueba o da un contraejemplo para las siguientes afirmaciones:
    • $\mathcal{O}(x) = X$ para todo $x\in X$.
    • Para cada $x,y \in X$ existe $g\in G$ tal que $g\cdot x = y$.
  4. Considera el grupo diédrico $D_{2(n)}$ actuando sobre sí mismo con conjugación.
    • Determina si la acción es fiel.
    • Encuentra el estabilizador de $a$, con $a$ la rotación de $\displaystyle\frac{2\pi}{n}$, y el de $b$ con $b$ la reflexión con respecto al eje $x$.
  5. Sea $G$ un grupo y $X$ un $G$-conjunto.
    • Determina si el hecho de que exista $x\in G$ tal que $G_x = \{e\}$ implica que la acción es fiel.
    • Determina si el hecho de que la acción sea fiel implica que exista $x\in G$ tal que $G_x=\{e\}$.

Más adelante…

Continuaremos estudiando las propiedades de las órbitas, en particular, el orden de las órbitas, ¿cómo se relaciona éste con el orden del grupo $G$? Daremos respuesta a ello en la siguiente entrada.

Entradas relacionadas