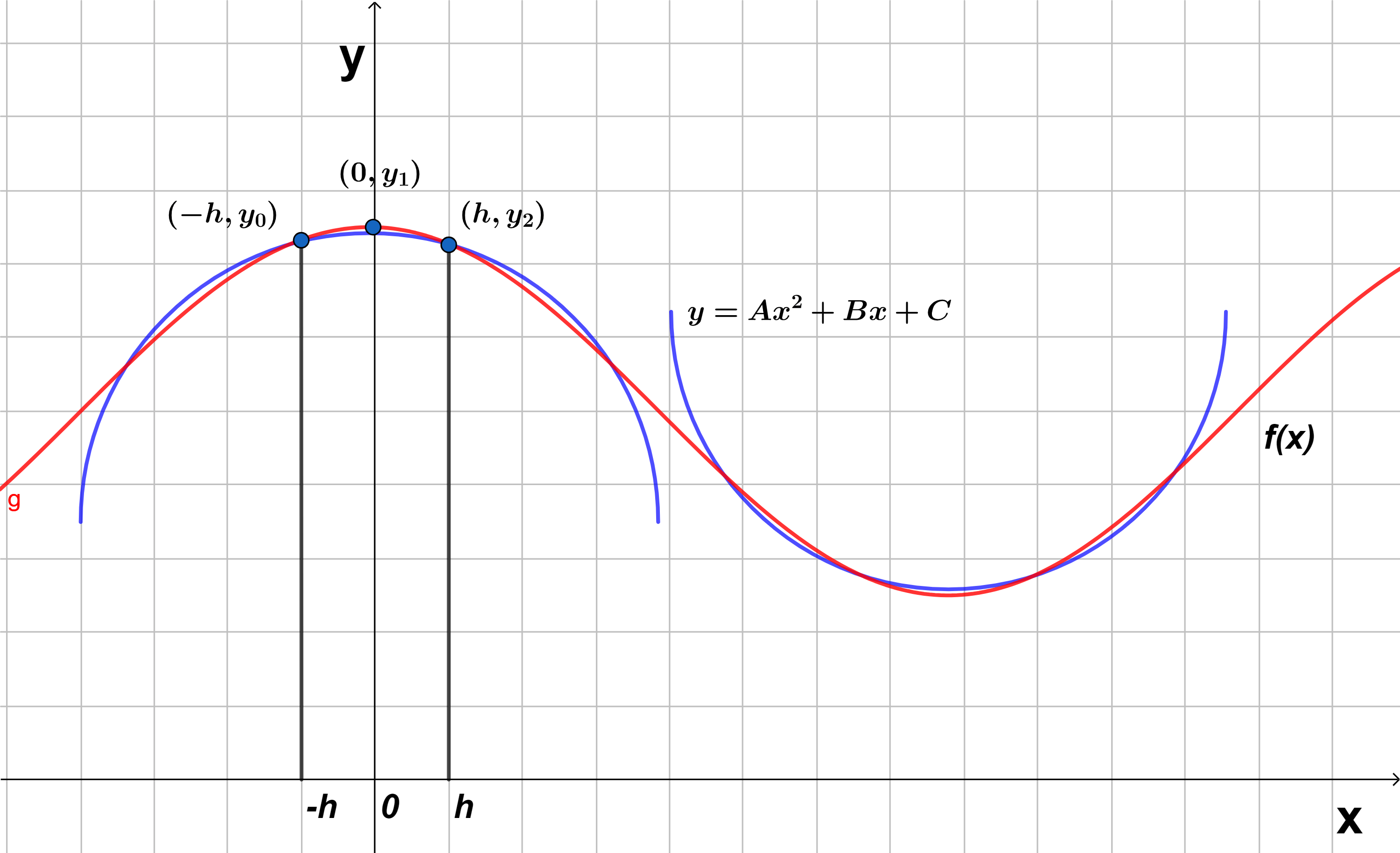Archivo de la etiqueta: metodo de simpson

Cálculo Diferencial e Integral II: Métodos Numéricos de Integración – Regla de Simpson

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En la sección anterior vimos dos métodos numéricos de integración: el método del punto medio y el método del trapecio. Otra regla de aproximación numérica a las integrales se llama regla de Simpson, el cual consiste en usar parábolas (como se muestra en la figura $1$) en lugar de segmentos de rectas para aproximarse a una curva.

Método de la regla de Simpson

Comencemos deduciendo la regla de Simpson.

Sea una curva dada por $f(x)$ en el plano en un intervalo $[a, b]$, dividimos el intervalo $[a, b]$ en $n$ subintervalos de igual longitud dado como:

$$\Delta x=\frac{b-a}{n}$$

En el que esta vez se requiere que $n$ sea un número par.

Figura 1: Regla de Simpson con aproximaciones parabólicas a la función $f(x)$.

La ecuación de una parábola está dada como:

$$y=Ax^{2}+Bx+C \tag{1}$$

Por lo que su área en el intervalo $[-h, h]$ es:

$$Área=\int_{-h}^{h}(Ax^{2}+Bx+C)dx=\left [ A\frac{x^{3}}{3}+B\frac{x^{2}}{2}+Cx+D \right ]\bigg{|}_{-h}^{h}$$

$$=\left [ A\frac{h^{3}}{3}+B\frac{h^{2}}{2}+Ch+D \right ]- \left [ A\frac{(-h)^{3}}{3}+B\frac{ (-h) ^{2}}{2}+C (-h) +D \right ]$$

$$=\left [ A\frac{h^{3}}{3}+B\frac{h^{2}}{2}+Ch+D \right ]+\left [ A\frac{h^{3}}{3}-B\frac{h^{2}}{2}+Ch-D \right ] $$

$$=\frac{2Ah^{3}}{3}+2Ch=h\frac{(2Ah^{2}+6C)}{3} \tag{2}$$

De la figura $1$ vemos que una de las curvas pasa por los puntos $(-h, y_{0})$, $(0, y_{1})$ y $(h, y_{2})$, evaluando estos puntos en la ecuación cuadrática $(1)$ se obtiene lo siguiente:

$$y_{0}=Ah^{2}-Bh+C$$

$$y_{1}=C$$

$$y_{2}=Ah^{2}+Bh+C$$

Si sumamos estas relaciones como:

$$y_{0}+4y_{1}+y_{2}= Ah^{2}-Bh+C +4C+ Ah^{2}+Bh+C= 2Ah^{2}+6C $$

Podemos expresar el área $(2)$ en términos de $y_{0}$, $y_{1}$ y $y_{2}$, como:

$$A_{1}=\frac{h}{3}(y_{0}+4y_{1}+y_{2})$$

Que es el área debajo de la parábola que pasa por los puntos $(x_{0}=-h, y_{0})$, $(x_{1}=0, y_{1})$ y $(x_{2}=h, y_{2})$, imaginemos que la segunda parábola intercepta en los puntos: $(x_{2}, y_{2})$, $(x_{3}, y_{3})$ y $(x_{4}, y_{4})$ entonces el área de esta segunda parábola es:

$$A_{2}=\frac{h}{3}(y_{2}+4y_{3}+y_{4})$$

Si sumamos todas las áreas hasta un n-esima parábola que se aproxima a la función $f(x)$, tendremos que el área total es:

$$\int_{a}^{b}f(x)dx\approx S_{n}=\frac{h}{3}(y_{0}+4y_{1}+y_{2})+\frac{h}{3}(y_{2}+4y_{3}+y_{4})+…+\frac{h}{3}(y_{n-2}+4y_{n-1}+y_{n})$$

$$=\frac{h}{3}(y_{0}+4y_{1}+2y_{2}+4y_{3}+…+2y_{n-2}+4y_{n-1}+y_{n})$$

Vemos que hay un patrón en los coeficientes:

$$1, \space 4, \space2, \space4, \space2 \space…. \space 2, \space4, \space1$$

Por lo que la regla de Simpson se define como:

$$\int_{a}^{b}f(x)dx\approx \frac{\Delta x}{3}(y_{0}+4y_{1}+y_{2})+\frac{\Delta x}{3}(y_{2}+4y_{3}+y_{4})+…+\frac{\Delta x}{3}(y_{n-2}+4y_{n-1}+y_{n})$$

$$=\frac{\Delta x}{3}(y_{0}+4y_{1}+2y_{2}+4y_{3}+…+2y_{n-2}+4y_{n-1}+y_{n}) \tag{3}$$

Con $\Delta x=\frac{b-a}{n}$, $n$ un número par, y los puntos $x_{i}$ los calculamos como:

$$x_{0}=a$$

$$x_{1}=a+\Delta x$$

$$…..$$

$$x_{n-1}=a+(n-1)\Delta x$$

$$x_{n}=b \tag{4}$$

Cota de error para la regla de Simpson

Para la estimación de la cota de error en la regla de Simpson, suponga que $|f^{4}(x)|\leq K$ para $a\leq x\leq b$ con $|f^{4}(x)|$ el valor absoluto de la cuarta derivada de la función. Si $E_{s}$ es el error relacionado con la regla de Simpson, entonces la cota de error para la regla de Simpson es:

$$E_{s}\leq\frac{K(b-a)^{5}}{180n^{4}}$$

Veamos un ejemplo.

Ejemplo

  • Usar la regla de Simpson para aproximar la integral $\int_{1}^{2}\frac{1}{x}dx$ con $n=10$.

Tenemos que $n=10$, $a=1$ y $b=2$ lo que implica que $\Delta x=\frac{b-a}{n}=0.1$.

Por la regla de Simpson $(3)$ y calculando los puntos $x_{i}$ $(4)$ tenemos que:

$$\int_{1}^{2}\frac{1}{x}dx\approx\ S_{10}=\frac{\Delta x}{3}\left [ f(1)+4f(1.1)+2f(1.2)+…+2f(1.8)+4f(1.9)+f(2) \right ]$$

$$=\frac{0.1}{3}\left [ \frac{1}{1}+\frac{4}{1.1}+\frac{2}{1.2}+\frac{4}{1.3}+\frac{2}{1.4}+\frac{4}{1.5}+\frac{2}{1.6}+\frac{4}{1.7}+\frac{2}{1.8}+\frac{4}{1.9}+\frac{1}{2}+ \right ]\approx 0.693150$$

Comparando este resultado con lo obtenido con la regla del punto medio y regla del trapecio, la regla de Simpson nos da una aproximación mucho mejor respecto a estos dos métodos, pues resulta que la regla de Simpson son promedios ponderados de la regla del punto medio y regla del trapecio, se puede demostrar que:

$$S_{2n}=\frac{1}{3}T_{n}+\frac{2}{3}M_{n}$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invito a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestre que: $S_{2n}=\frac{1}{3}T_{n}+\frac{2}{3}M_{n}$
  2. ¿Qué tan grande debe de ser n para que al utiliza la regla de Simpson al aproximar la integral $\int_{1}^{2}\frac{1}{x}dx$, sea exacta hasta dentro de 0.0001?
    1. Use la regla de Simpson con n=10 para aproximar la integral $\int_{0}^{1} e^{x^{2}}dx$
    2. Estime el error con esta aproximación
    1. Estimar la integral con n=3: $\int_{0}^{2} x^{3}dx$
    2. En este caso, ¿la regla de Simpson es exacta? ¿Porque?

Más adelante…

En esta sección vimos la regla de Simpson que consiste en otro método de aproximación numérica para las integrales por medio de parábolas y que es este método es un promedio ponderado de los métodos del punto medio y del trapecio. Aunque existen más métodos numéricos para aproximar integrales, solo veremos estos métodos. En la siguiente sección veremos el teorema del valor medio para las integrales.

Entradas relacionadas