Archivo de la etiqueta: longitud en coordenadas polares

Cálculo Diferencial e Integral II: Longitud de arco en coordenadas polares

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En la sección anterior vimos como calcular el área de una curva que está acotada por una curva y el área entre dos curvas en coordenadas polares, en esta sección veremos como calcular la longitud de arco de una curva en coordenadas polares, la idea de calcular de la longitud es la misma para calcular la longitud de una curva en coordenadas cartesianas, en esta ocasión, lo haremos en coordenadas polares, pero para esto veamos un teorema para la longitud de arco para las curvas paramétricas.

Longitud de arco para curvas paramétricas

Teorema. Si una curva $C$ se describe mediante las ecuaciones paramétricas $x=f(t)$ y $y=g(t)$, con $\alpha \leq t \leq \beta$, donde $f’$ y $g’$ son continuas en el intervalo $[\alpha, \beta]$, entonces la longitud de $C$ que es recorrida una sola vez cuando $t$ aumenta desde $\alpha$ hasta $\beta$, se calcula como:

$$L=\int_{\alpha}^{\beta} \sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt}\right )^{2}}dt$$

Demostración:

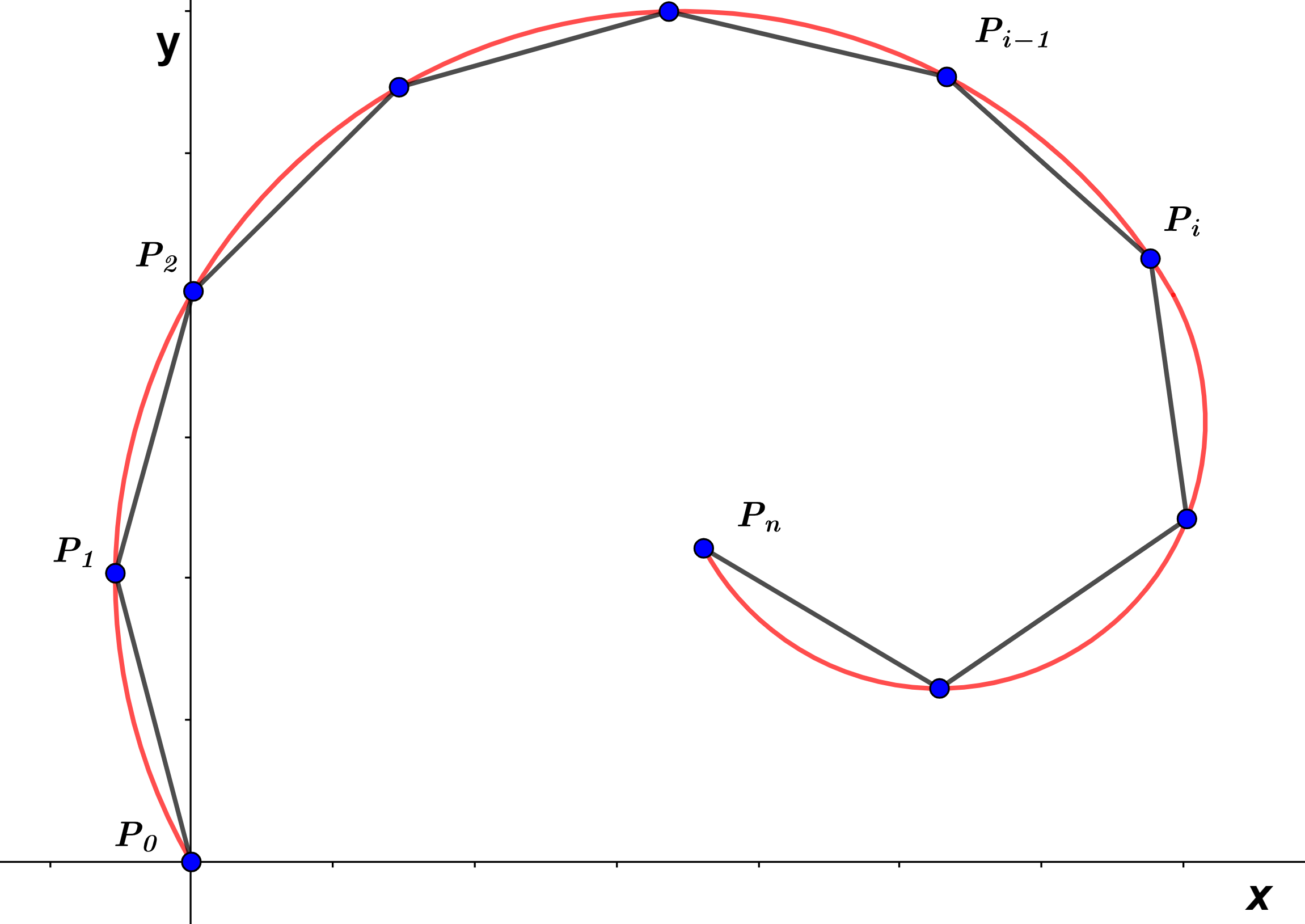
Sea $C$ la curva en un intervalo $[\alpha, \beta]$, se divide este intervalo en $n$ subintervalos $t_{0}, \space t_{1},…., \space t_{n}$ con longitud $\Delta t$. Aproximamos la curva $C$ con polígonos con vértices $P_{0}, \space, P_{1}, \space, …., P_{n}$, como se muestra en la figura $(1)$.

Figura 1: Aproximación de polígonos (líneas negras) a una curva $C$ (curva roja).

Si el número de polígonos tiende a infinito, es decir, $n \to \infty$, entonces:

$$L=\lim_{n \to \infty} \sum_{i=1}^{n}|P_{i-1}-P_{i}|$$

Aplicamos el teorema de valor medio a $f$ en el intervalo $[t_{i-1},t_{i}]$, encontramos un número $t^{*}_{i}$ tal que:

$$f(t_{i})-f(t_{i-1})=f'(t^{*}_{i})(t_{i}-t_{i-1})$$

Lo podemos reescribir en términos de deltas como:

$$\Delta x_{i}=f'(t^{*}_{i})\Delta t$$

Análogamente, hacemos lo mismo para $g(t)$, aplicando el teorema del valor medio encontrando un número $t^{**}_{i}$ tal que:

$$\Delta y_{i}=g'(t^{**}_{i})\Delta t$$

Por lo que la longitud la podemos escribir como:

$$L= \lim_{n \to \infty }\sum_{i=1}^{n} |P_{i-1}-P_{i}|=\lim_{n \to \infty }\sum_{i=1}^{n} \sqrt{(\Delta x)^{2}+(\Delta y)^{2}}$$

$$=\lim_{n \to \infty }\sum_{i=1}^{n}\sqrt{(f'(t^{*}_{i})\Delta t)^{2}+(g'(t^{**}_{i})\Delta t)^{2}}=\lim_{n \to \infty }\sum_{i=1}^{n}\sqrt{(f'(t^{*}_{i}))^{2}+(g'(t^{**}_{i}))^{2}}\Delta t$$

Si $f’$ y $g’$ son continuas, entonces el límite de la suma es el mismo que si $t^{*}_{i}$ y $t^{**}_{i}$ fueran iguales, por lo que:

$$L=\int_{\alpha}^{\beta}\sqrt{\left [ f'(t) \right ]^{2}+\left [ g'(t) \right ]^{2}}dt$$

En notación de Leibniz tenemos que:

$$L=\int_{\alpha}^{\beta} \sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt}\right )^{2}}dt \tag{1}$$

$\square$

Este teorema nos servirá para calcular la longitud de una curva en coordenadas polares.

Longitud de arco en coordenadas polares

Sea una curva polar dada por $r=f(\theta)$, en un intervalo $a \leq \theta \leq b$, podemos escribir las ecuaciones paramétricas como:

$$x=r\cos(\theta)=f(\theta)\cos(\theta) \hspace{2cm} y=r\sin(\theta)=f(\theta)\sin(\theta)$$

Derivamos respecto a $\theta$ las dos anteriores ecuaciones, por lo que:

$$\frac{dx}{d\theta}=\frac{dr}{d\theta}\cos(\theta)-r\sin(\theta) \hspace{2cm} \frac{dy}{d\theta}=\frac{dr}{d\theta}\sin(\theta)+r\cos(\theta)$$

Elevando al cuadrado, y sumando las derivadas, obtenemos:

$$\left ( \frac{dx}{d\theta} \right )^{2}+\left ( \frac{dy}{d\theta} \right )^{2}=\left (\frac{dr}{d\theta}\cos(\theta)-r\sin(\theta) \right )^{2}+\left (\frac{dr}{d\theta}\sin(\theta)+r\cos(\theta) \right )^{2}$$

$$=\left (\frac{dr}{d\theta}\right )^{2}\cos^{2}(\theta)-2\frac{dr}{d\theta}\cos(\theta)r\sin(\theta)+r^{2}\sin^{2}(\theta)+\left (\frac{dr}{d\theta}\right )^{2}\sin^{2}(\theta)+2\frac{dr}{d\theta}\sin(\theta)r\cos(\theta)+r^{2}\cos^{2}(\theta)$$

Utilizando que $\sin^{2}(\theta)+\cos^{2}(\theta)=1$, entonces:

$$\left ( \frac{dx}{d\theta} \right )^{2}+\left ( \frac{dy}{d\theta} \right )^{2}=\left (\frac{dr}{d\theta}\right )^{2}+r^{2}$$

Utilizando la relación $(1)$, suponiendo que $f’$ es continua, entonces la longitud de una curva polar está dada como:

$$L=\int_{a}^{b} \sqrt{ r^{2}+\left ( \frac{dr}{d\theta}\right )^{2}}d\theta$$

Ejemplo

  • Encontrar la longitud del cardioide dado como: $r=1-\cos(\theta)$

En este caso, tenemos que:

$$r^{2}+\left ( \frac{dr}{d\theta}\right )^{2}=(1-\cos(\theta))^{2}+\sin^{2}(\theta)=1-2\cos(\theta)+\cos^{2}(\theta)+\sin^{2}(\theta)=2-2\cos(\theta)$$

Así la longitud de arco es:

$$L=\int_{0}^{2\pi} \sqrt{2-2\cos(\theta)}d\theta=\int_{0}^{2\pi} \sqrt{4\sin^{2}(\frac{\theta}{2})}d\theta=\int_{0}^{2\pi} \sqrt{4\sin^{2}(\frac{\theta}{2})}d\theta$$

$$=2\int_{0}^{2\pi}\sin(\frac{\theta}{2})d\theta=\left [ -4\cos(\frac{\theta}{2}) \right ]\bigg|^{2\pi}_{0}=4+4=8$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentre la longitud de la curva polar dada como $r=3\sin(\theta)$, $0 \leq \theta \leq \frac{\pi}{3}$.
  2. Encuentre la longitud de la curva polar dada como $r=e^{2\theta)$, $0 \leq \theta \leq 2\pi$.
  3. Encuentre la longitud de la curva polar dada como $r=\theta^{2}$, $0 \leq \theta \leq 2\pi$.
  4. Encuentre la longitud de la curva polar de un pétalo de rosa dada como $r=\cos(2\theta)$.
  5. Encuentre la longitud de la curva polar de un cardiode dado como $r=a(1+\cos(\theta))$, $a > 0$.

Más adelante…

En esta sección vimos un teorema que nos dice como calcular la longitud de una curva dada por dos curvas paramétricas en general, aplicando este teorema, vimos que se puede utilizar para poder calcular la longitud de una curva en coordenadas polares. En la siguiente sección veremos las funciones hiperbólicas.

Entradas relacionadas