Introducción
En la sección anterior vimos como calcular el área delimitada entre dos curvas, otra aplicación de la integral es calcular la longitud de una curva a lo largo de un intervalo dado, lo cual veremos en esta sección. Comenzamos deduciendo la fórmula de la longitud de arco o también llamada la longitud de curva.
Longitud de arco
Supóngase que tenemos una curva $C$ que se define mediante la ecuación $y=f(x)$, continua en el intervalo $[a, b]$. El objetivo es medir la longitud de esa curva en el intervalo dado $[a, b]$, para esto se divide el intervalo $[a, b]$ en $n$ subintervalos con puntos extremos $x_{0}, x_{1}, …, x_{n}$ y amplitud $\Delta x$, por tanto, conseguimos un polígono con vértices $P_{0}, P_{1}, …, P_{n}$ para aproximar a la curva $C$ como se muestra en la figura $(1)$. Calculamos la distancia entre los vértices $P_{i-1}$ y $P_{i}$, para aproximarnos mejor a la curva $C$, sumamos $n$ vértices y tomamos el límite cuando $n \to \infty$, tenemos que la longitud de la curva la podemos aproximar como:
$$L=\lim_{n \to \infty} \sum_{i=1}^{n}d(P_{i-1},P_{i})$$
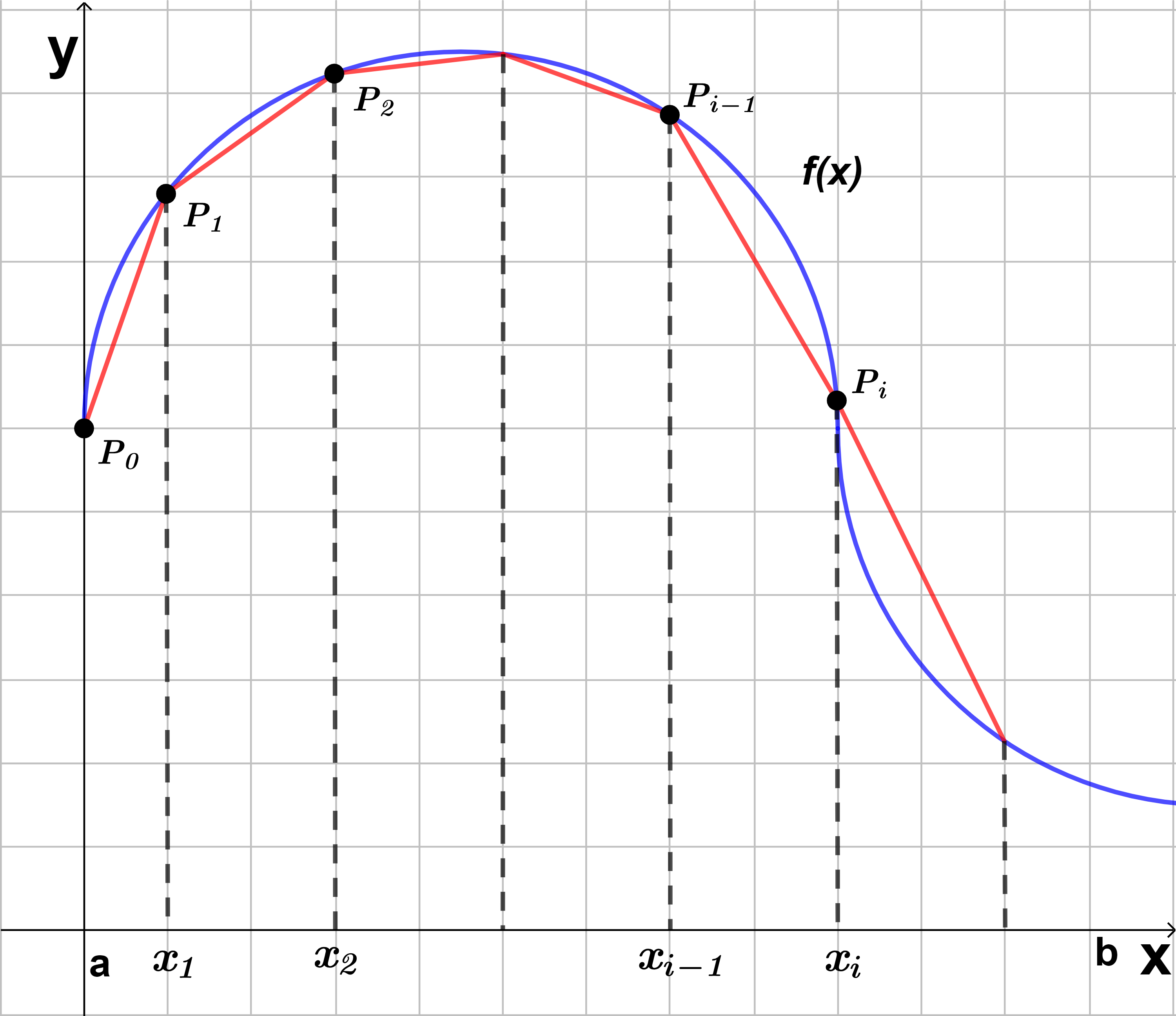
Podemos reescribir a $d(P_{i-1},P_{i})$ como:
$$d(P_{i-1},P_{i})=\sqrt{(x_{i}-x_{i-1})^{2}+(y_{i}-y_{i-1})^{2}}=\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}$$
Utilizamos el teorema de valor medio y la aplicamos a la función $f(x)$ en el intervalo $[x_{i-1},x_{i}]$, lo cual encontramos un número $x^{*}_{i}$ tal que:
$$f(x_{i})-f(x_{i-1})=f'(x^{*}_{i})(x_{i}-x_{i-1})$$
Podemos reescribir la anterior relación como: $\Delta y=f'(x^{*}_{i})\Delta x$ así, se tiene que: $$d(P_{i-1},P_{i})=\sqrt{(\Delta x)^{2}+[f'(x^{*}_{i})\Delta x]^{2}}=\sqrt{1+[f'(x^{*}_{i})]^{2}}\sqrt{(\Delta x)^{2}}=\sqrt{1+[f'(x^{*}_{i})]^{2}}{\Delta x}$$
Por tanto:
$$L=\lim_{n \to \infty }\sum_{i=1}^{n}\sqrt{(1+[f'(x^{*}_{i})]^{2}}{\Delta x}$$
Si $n \to \infty$ entonces la fórmula de longitud de arco donde $f'(x)$ es continua en $[a, b]$ esta dada como:
$$L=\int_{a}^{b}\sqrt{1+[f'(x)]^{2}}dx \tag{1}$$
En notación de Leibniz, se puede reescribir la longitud de arco como:
$$L=\int_{a}^{b}\sqrt{1+\left ( \frac{dy}{dx} \right )^{2}}dx$$
La longitud de curva no depende de la elección de los ejes coordenados, si una curva tiene como ecuación $x=g(y)$, con $c\leq y\leq d$ y $g'(y)$ continua, entonces la longitud de arco se reescribe como.
$$L=\int_{c}^{d}\sqrt{1+\left ( \frac{dx}{dy} \right )^{2}}dy \tag{2}$$
Veamos los ejercicios a continuación para el cálculo de algunas longitudes de arco de algunos funciones en un intervalo.
Ejemplos
- Determinar la longitud de arco de la parábola dada como: $y^{2}=x^{3}$ entre los puntos $(1, 1)$ y $(4, 8)$.
Tenemos que $y^{2}=x^{3} \Rightarrow y=x^{\frac{3}{2}}$
Derivando la función anterior, se tiene que:
$$\frac{dy}{dx}=\frac{3}{2}x^{1/2}$$
Así, utilizando la relación $(1)$, la longitud del arco se calcula como:
$$L=\int_{1}^{4}\sqrt{1+\left (\frac{3}{2}x^{1/2} \right )^{2}}dx$$
Integramos por el método de cambio de variable.
Sea $u=1+\frac{9}{4}x \space \Rightarrow \space du=\frac{9}{4}dx$, cambiamos los límites de integración, si $x=1 \Rightarrow u=\frac{13}{4}$, si $x=4 \Rightarrow u=10$, por tanto, la integral la reescribimos como:
$$\int_{\frac{13}{4}}^{10}\frac{4}{9}\sqrt{u}du=\frac{4}{9}\frac{2}{3}\left [ u^{2/3} \right ]\bigg|_{10}^{\frac{13}{4}}=\frac{8}{27}\left [ 10^{3/2}-\left ( \frac{13}{4} \right )^{3/2} \right ]=\frac{1}{27}\left ( 80\sqrt{10}-13\sqrt{13} \right )$$
- Encuentre la longitud de arco de la parábola $x=y^{2}$ de $(0, 0)$ a $(1, 1)$
Tenemos que la curva es $x=y^{2} \Rightarrow x’=2y$, en este caso tenemos que la curva es función de $f(y)$ por lo que utilizamos la relación $(2)$, así la longitud de arco lo calculamos como:
$$L=\int_{0}^{1}\sqrt{1+(2y)^{2}}dy=\int_{0}^{1}\sqrt{1+4y^{2}}dy$$
Utilizamos el método de sustitución trigonométrica, observamos en que caso se puede aplicar para resolver esta integral, por lo que hacemos la sustitución siguiente:
$$y=\frac{1}{2}\tan(\theta ) \Rightarrow dy=\frac{1}{2}\sec^{2}(\theta )d\theta$$
Así: $\sqrt{1+4y^{2}}=\sqrt{1+\tan(\theta)^{2}}=\sec(\theta)$, veamos los límites de integración:
Si $y=0 \Rightarrow \theta=0 $ y si $y=1 \Rightarrow \tan(\theta)=2 \Rightarrow \theta=arctan(2)$ por tanto:
$$L=\int_{0}^{\arctan(2)}\sec(\theta )\frac{1}{2}\sec^{2}(\theta)d\theta=\frac{1}{2}\int_{0}^{\arctan(2)}\sec^{3}(\theta)d\theta$$
Recordemos que esta integral la resolvimos en la entrada de productos de potencias de tan(x) y sec(x), por lo que:
$$L=\frac{1}{2}\int_{0}^{\arctan(2)}\sec^{3}(\theta)d\theta=\frac{1}{2}\frac{1}{2}\left [ \sec(\theta)\tan(\theta)+ln(|\sec(\theta)+\tan(\theta)|) \right ]\bigg|_{0}^{\arctan(2)}$$
$$=\frac{1}{4}\left [\sec(\arctan(2))\tan(\arctan(2))+ln(|\sec(\arctan(2))+\tan(\arctan(2))|) -0 \right]$$
Puesto que:
$$\tan(\arctan(2))=2 \Rightarrow tan^{2}(arctan(2))=4$$ y
$$\sec^{2}(\theta)=1+\tan^{2}(\theta) \Rightarrow \sec^{2}(\arctan(2))=1+4 \Rightarrow \sec(\arctan(2))=\sqrt{5}$$ Así la longitud de arco es:
$$L=\frac{\sqrt{5}}{2}+\frac{ln(\sqrt{5}+2)}{4}$$
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Calcule la longitud de arco de la curva que tiene como ecuación $y=ln(\cos(x))$ en $[0, \frac{\pi }{4}]$
- Calcule la longitud de arco de la curva que tiene como ecuación $y=1+6x^{\frac{3}{2}}$ en $[0, 1]$
- Calcule la longitud de arco de la curva que tiene como ecuación $x=\sin(y)$ en $0\leq y \leq \pi$
- Calcule la longitud de arco entre $(x_{1}, y_{1})$ y $(x_{2}, y_{2})$ de la gráfica $y=mx+b$
- Muestre que la longitud de la circunferencia de radio $1$ es $2\pi$, recuerde que la curva viene dada por $x^{2}+y^{2}=1$ Hint: Tome un cuarto de la curva e integre.
Más adelante…
En esta sección vimos como calcular la longitud de arco de una curva que tiene como ecuación $y=f(x)$ o $x=f(y)$ dentro de un intervalo dado. Como ya sabemos como calcular áreas, en la siguiente entrada veremos como calcular el volumen de un sólido, para esto, veremos el método de secciones transversales.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Área entre curvas – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral: Cálculo de volúmenes por secciones transversales y por rotación alrededor de un eje – El blog de Leo (nekomath.com)


