Introducción
Esta es una continuación de la entrada anterior donde vimos algunas propiedades de hileras armónicas de puntos, esta vez nos enfocaremos en propiedades de un haz armónico de rectas, que nos permitirán definir al cuadrilátero armónico.
Haz de rectas
Definición 1. Si cuatro rectas $PA$, $PC$, $PB$, $PD$ concurren en $P$, decimos que forman un haz de rectas y que $P$ es el vértice del haz, denotamos al haz como $P(ACBD)$.
Teorema. 1 Sea $P(ACBD)$ un haz de rectas donde $A$, $C$, $B$, $D$, son colineales, considera $A’$, $B’$, $C’$, $D’$, las intersecciones de cualquier otra transversal al haz, entonces $(A, B; C, D) = (A’, B’; C’, D’)$.
Demostración. Aplicamos la ley de los senos a $\triangle PAC$, $\triangle PCB$, $\triangle PBD$ y $\triangle PAD$.
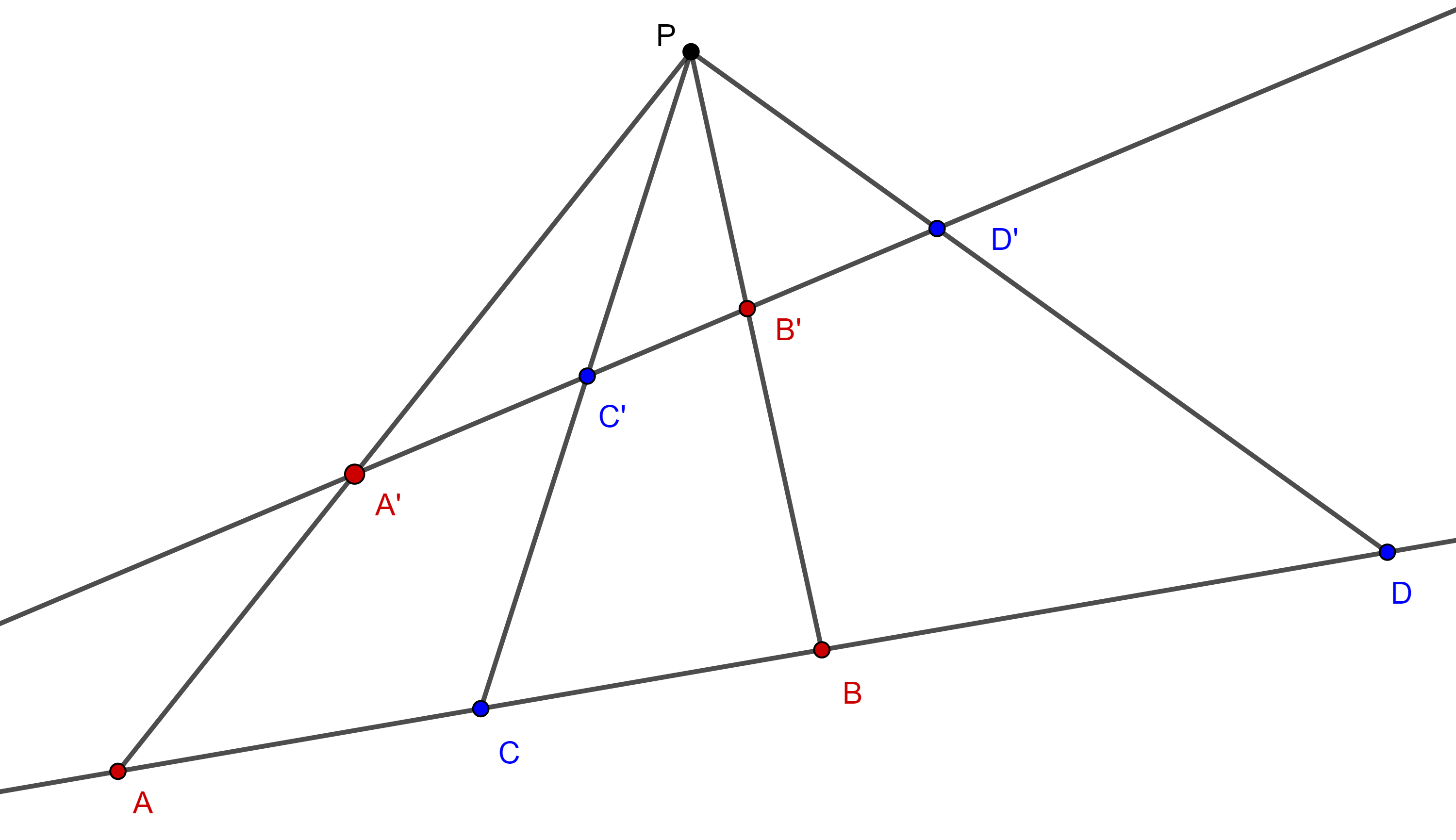
$\dfrac{AC}{\sin \angle APC} =\dfrac{PC}{\sin \angle CAP}$,
$\dfrac{CB}{\sin \angle CPB} =\dfrac{PC}{\sin \angle PBC}$,
$\dfrac{DB}{\sin \angle BPD} =\dfrac{PD}{\sin \angle DBP}$,
$\dfrac{AD}{\sin \angle APD} =\dfrac{PD}{\sin \angle DAP}$.
De lo anterior calculamos,
$(A, B; C, D) = \dfrac{AC}{CB} \dfrac{DB}{AD}$
$=\dfrac{\dfrac{\sin \angle APC}{\sin \angle CAP} \dfrac{\sin \angle BPD}{\sin \angle DBP}}{\dfrac{\sin \angle CPB}{\sin \angle PBC} \dfrac{\sin \angle APD}{\sin \angle DAP}}$
$\begin{equation} = \dfrac{\sin \angle APC}{\sin \angle CPB} \dfrac{\sin \angle BPD}{\sin \angle APD}. \end{equation}$
La última igualdad se debe a que $\angle CAP = \angle DAP$ y $\sin \angle PBC = \sin \angle DBP$, por ser $\angle PBC$ y $\angle DBP$ suplementarios.
Si hacemos el mismo procedimiento, esta vez con los puntos $A’$, $C’$, $B’$, $D’$, obtendremos el mismo resultado ya que $\angle APC = \angle A’PC’$, $\angle CPB = \angle C’PB’$, $\angle BPD = \angle B’PD’$ y $\angle APD = \angle A’PD’$.
Por lo tanto $(A, B; C, D) = (A’, B’; C’, D’)$.
$\blacksquare$
Definición 2. Dado un haz de rectas $P(ACBD)$, si $A$, $C$, $B$ y $D$ son colineales, definimos la razón cruzada $P(A, B; C, D)$ del haz como la razón cruzada $(A, B; C, D)$, de la hilera de puntos $ACBD$.
Equivalentemente, por la ecuación $(1)$, podemos definir, $P(A, B; C, D) = \dfrac{\sin \angle APC}{\sin \angle CPB} \dfrac{\sin \angle BPD}{\sin \angle APD}$.
Si $P(A, B; C, D) = – 1$, decimos que el haz es armónico y que $PA$, $PB$ son rectas conjugadas armónicas respecto de $PC$ y $PD$ o que $PC$, $PD$ son conjugadas armónicas respecto de $PA$ y $PD$.
Ejemplo
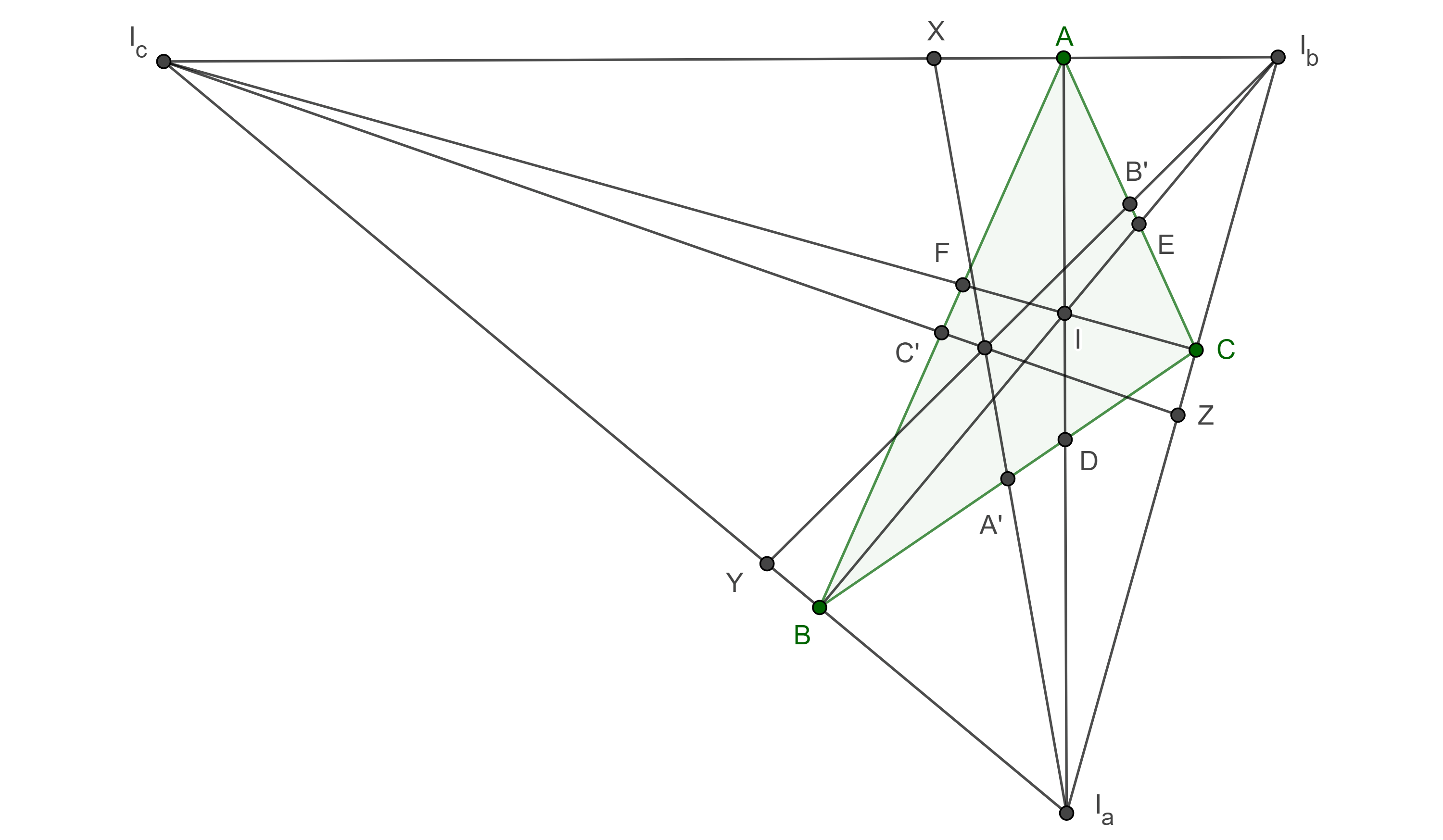
Proposición 1. Las rectas que unen los excentros de un triángulo con los puntos medios de los lados del triángulo relativos a esos excentros son concurrentes.
Demostración. Sean $I_a$, $I_b$, $I_C$, los excentros de un triángulo $\triangle ABC$, $A’$, $B’$, $C’$ los puntos medio de $BC$, $CA$ y $AB$ respectivamente, consideremos $X = I_aA’ \cap I_bI_c$, $Y = I_bB’ \cap I_aI_c$, $Z = I_cC’ \cap I_aI_b$; $D = I_aA \cap BC$, $E = I_bB \cap CA$, $F = I_cC \cap AB$.
Consideremos los haces $I_a(CDA’B)$, $I_b(AB’EC)$, $I_c(BC’FA)$, por el teorema 1, tenemos lo siguiente:
$(A’, D; B, C) = (X, A; I_c, I_b)$,
$(B’, E; A, C) = (Y, B; I_c, I_a)$,
$(C’, F; B, A) = (Z, C; I_a, I_b)$.
Esto es,
$\begin{equation} \dfrac{A’B}{BD} \dfrac{CD}{A’C} = \dfrac{XI_c}{I_cA} \dfrac{I_bA}{XI_b}, \end{equation}$
$\begin{equation} \dfrac{B’A}{AE} \dfrac{CE}{B’C} = \dfrac{YI_c}{I_cB} \dfrac{I_aB}{YI_a}, \end{equation}$
$ \begin{equation} \dfrac{C’B}{BF} \dfrac{AF}{C’A} = \dfrac{ZI_a}{I_aC} \dfrac{I_bC}{ZI_b}. \end{equation}$
Como $AD$, $BE$, $CF$; $I_aA$, $I_bB$, $I_cC$, concurren en el incentro $I$ de $\triangle ABC$, aplicando el teorema de Ceva a los triángulos $\triangle ABC$ y $\triangle I_aI_bI_c$ tenemos:
$\dfrac{AF}{FB} \dfrac{BD}{DC} \dfrac{CE}{EA} = 1$,
$\dfrac{I_aC}{CI_b} \dfrac{I_bA}{AI_c} \dfrac{I_cB}{BI_a} = 1$.
Recordemos que $A’$, $B’$, $C’$ son los puntos medios de $BC$, $CA$ y $AB$, empleando segmentos dirigidos y tomando en cuenta lo anterior, si hacemos el producto del inverso de $(2)$ con $(3)$ y $(4)$, obtenemos:
$\dfrac{I_aZ}{ZI_b} \dfrac{I_cX}{XI_b} \dfrac{I_cY}{YI_a} = 1$.
Por el teorema de Ceva, $I_aX = I_aA’$, $I_bY = I_bB’$, $I_cZ = I_cC’$, son concurrentes.
$\blacksquare$
Haz armónico
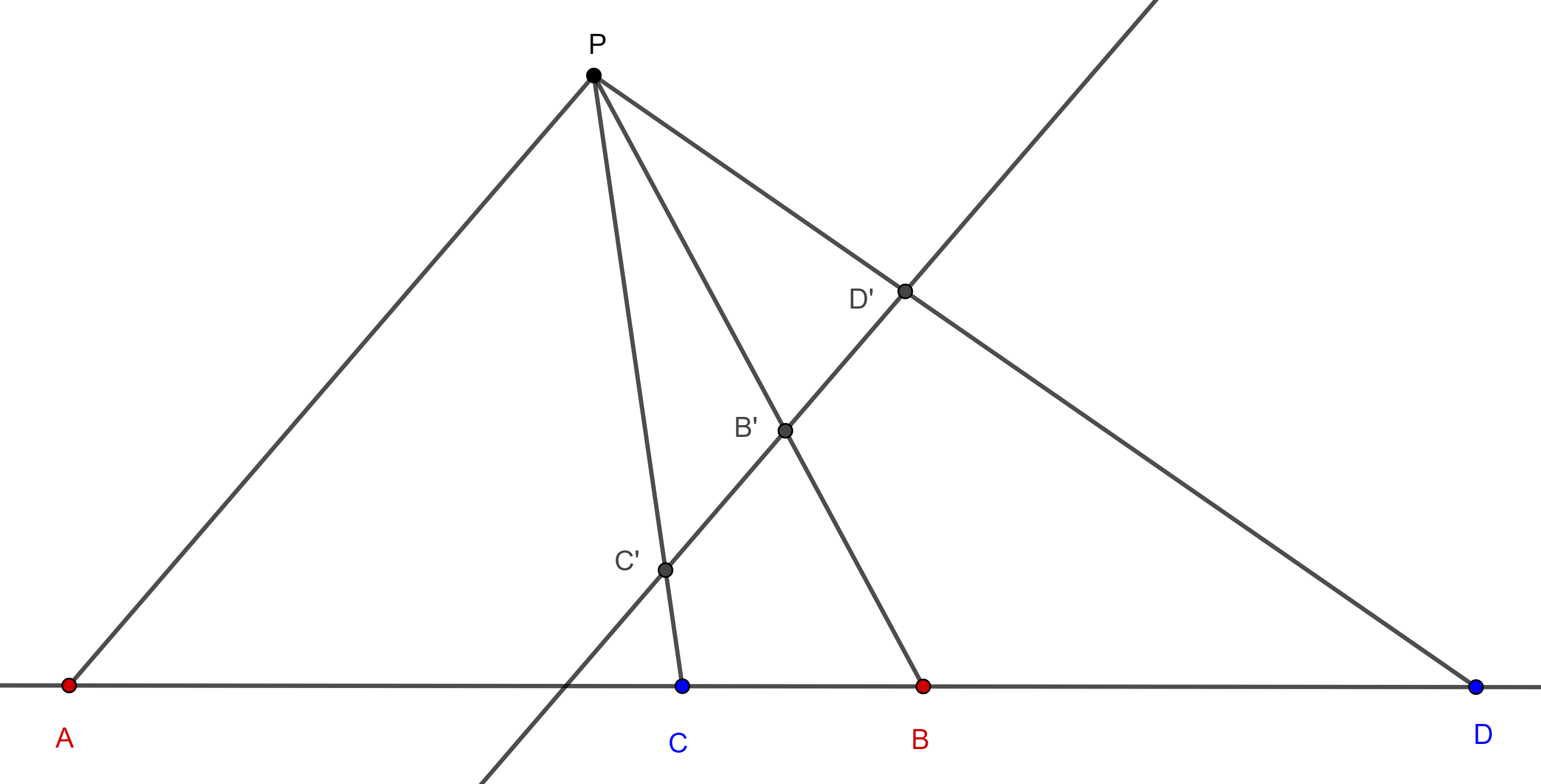
Proposición 2. Una recta, paralela a alguna de las rectas de un haz, es dividida en dos segmentos iguales por las otras tres rectas del haz si y solo si el haz es armónico.
Demostración. Sean $P(ACBD)$ un haz de rectas con $A$, $C$, $B$, $D$, colineales en ese orden, $l$ paralela a $PA$, $C’ = l \cap PC$, $B’ = l \cap PB$, $D’ = l \cap PD$.
Aplicamos la ley de los senos a $\triangle C’PB’$ y $\triangle B’PD’$
$\dfrac{C’B’}{\sin \angle C’PB’} =\dfrac{PB’}{\sin \angle B’C’P}$,
$\dfrac{D’B’}{\sin \angle B’PD’} =\dfrac{PB’}{\sin \angle PD’B’}$.
Por lo tanto,
$\dfrac{D’B’}{C’B’} = \dfrac{\sin \angle B’C’P}{\sin \angle C’PB’} \dfrac{\sin \angle B’PD’}{\sin \angle PD’B’}$.
Por la ecuación $(1)$
$(A, B; C, D) = \dfrac{\sin \angle APC}{\sin \angle CPB} \dfrac{\sin \angle BPD}{\sin \angle APD}$.
Como $PA \parallel C’B’D’$, entonces $\angle APC = \angle B’C’P$ y $\angle APD$, $\angle PD’B’$ son suplementarios, además $\angle CPB = \angle C’PB’$ y $\angle BPD = \angle B’PD’$.
Por lo tanto $(A, B; C, D) = \dfrac{D’B’}{C’B’}$.
Como resultado, $(A, B; C, D) = -1 \Leftrightarrow |D’B’| = |C’B’|$.
$\blacksquare$
Proposición 3. Si dos rectas conjugadas de un haz armónico son perpendiculares entonces son las bisectrices del ángulo formado por las otras dos rectas del haz.
Demostración. Sea $P(ACBD)$ un haz armónico, supongamos que $PA \perp PB$ (figura 3), sean $l$ una recta paralela a $PA$ y $C’$, $B’$, $D’$, las intersecciones de $l$ con $PC$, $PB$, $PD$ respectivamente.
Por la proposición anterior $C’B’ = B’D’$, como $PA \perp PB$ entonces $PB \perp C’D’$.
Por lo tanto, $\triangle PC’D’$ es isósceles y así, $PA$ y $PB$ son las bisectrices externa e interna de $\angle C’PD’$.
$\blacksquare$
Proposición 4. Si tenemos dos hileras armónicas $ACBD$ y $A’C’B’D’$ tales que $AA’$, $BB’$, $CC’$ concurren en un punto $P$ entonces $DD’$ también pasa por $P$.
Demostración. Sea $X = PD \cap A’C’B’D’$, por el teorema 1, $X$ es el conjugado armónico de $C’$ respecto de $A’B’$, por lo tanto $X = D’$.
$\blacksquare$
Cuadrilátero armónico
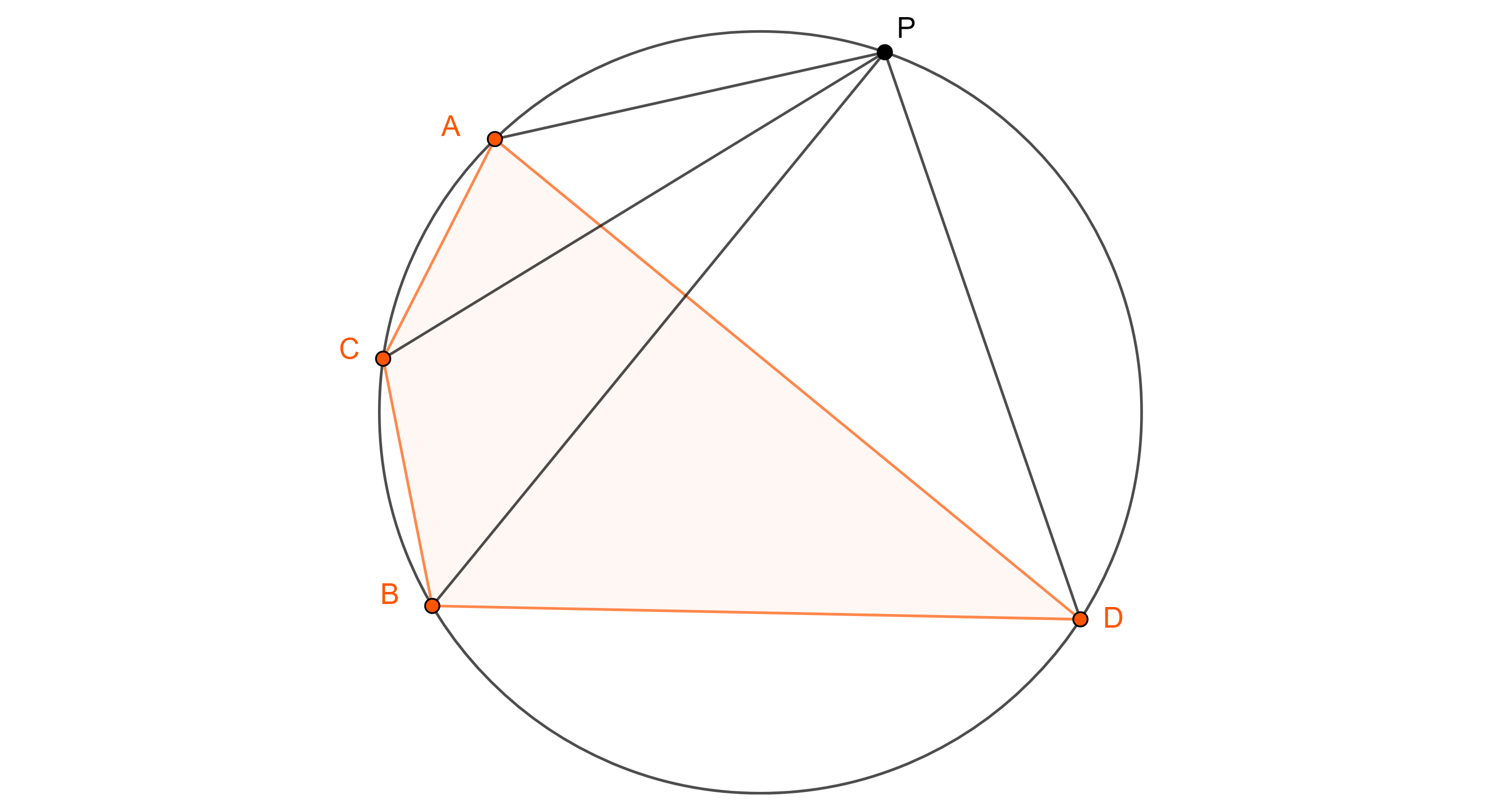
Teorema 2. Sean $\square ACBD$ un cuadrilátero cíclico, en ese orden cíclico, y $P$ un punto en su circuncírculo, entonces la razón cruzada del haz $P(ACBD)$ no depende de la posición de $P$.
Demostración. Sea $R$ el circunradio de $\square ABCD$, aplicamos la ley extendida de los senos a $\triangle APC$, $\triangle CPB$, $\triangle BPD$ y $\triangle APD$.
$\dfrac{AC}{\sin \angle APC} = \dfrac{CB}{\sin \angle CPB} = \dfrac{DB}{\sin \angle BPD}$
$= \dfrac{AD}{\sin \angle APD} = \dfrac{1}{2R}$.
Por lo tanto,
$P(A, B; C, D) = \dfrac{\sin \angle APC}{\sin \angle CPB} \dfrac{\sin \angle BPD}{\sin \angle APD}$
$= \dfrac{AC}{CB} \dfrac{DB}{AD}$.
$\blacksquare$
Definición 3. Definimos la razón cruzada de cuatro puntos cíclicos $A$, $B$, $C$, $D$, como $(A, B; C, D) = P(A, B; C, D)$, para cualquier punto $P$ en la misma circunferencia.
De manera equivalente, por el teorema 2, podemos definir $(A, B; C, D) = \dfrac{AC}{CB} \div \dfrac{AD}{DB}$, la cual tomamos como positiva si $AB$ y $CD$ no se intersecan dentro de la circunferencia y como negativa en caso contrario.
Si $(A, B; C, D) = – 1$, decimos que $\square ACBD$ es un cuadrilátero armónico.
Construcción del conjugado armónico en una circunferencia.
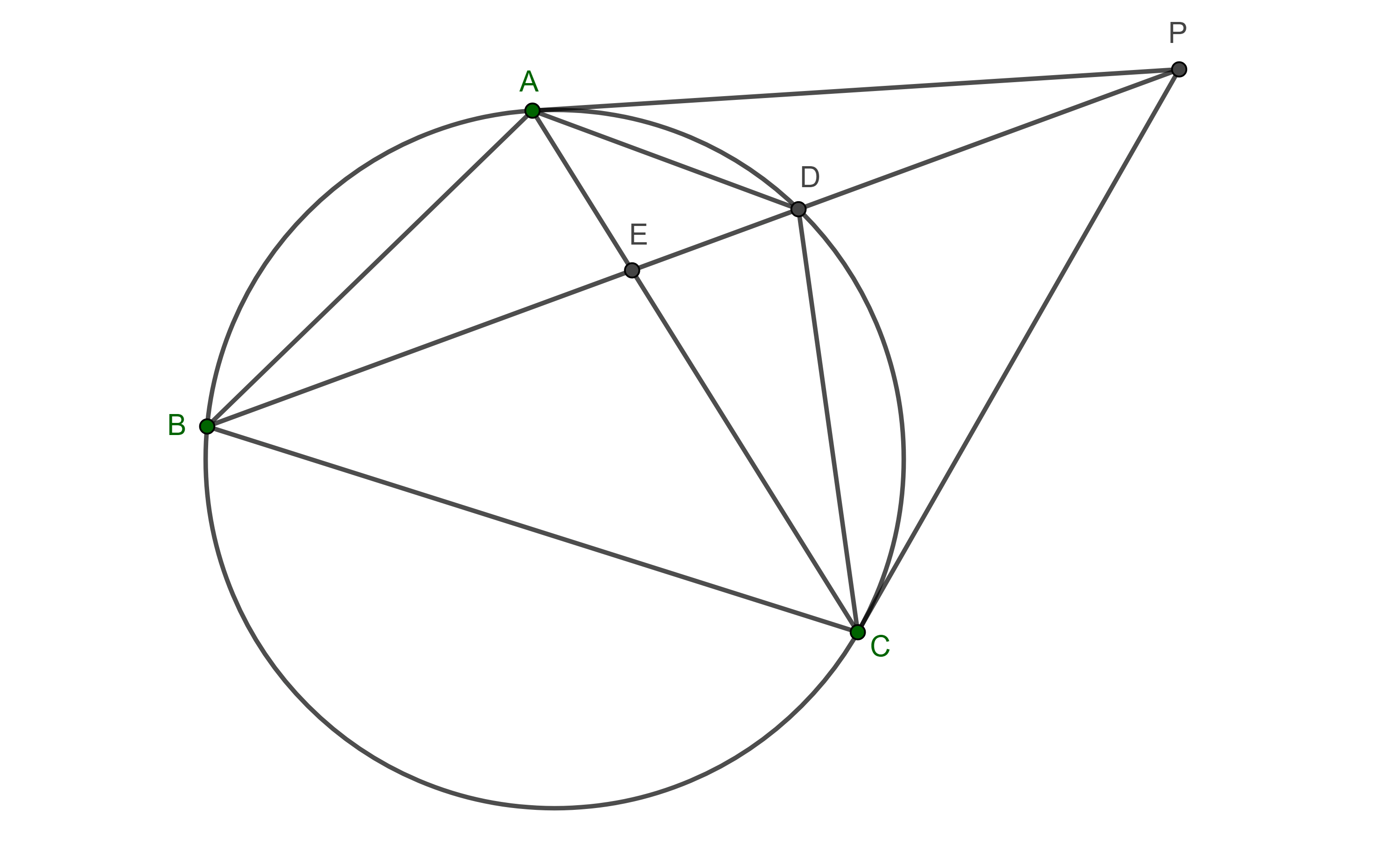
Proposición 5. Sean $\Gamma$ el circuncírculo de un triángulo $\triangle ABC$, $P$ la intersección de las tangentes a $\Gamma$ por $A$ y $C$, $D = PB \cap \Gamma$, $D \neq B$, entonces $\square ABCD$ es un cuadrilátero armónico.
Demostración. Como $\angle DBA = \angle DAP$ y $\angle CBD = \angle PCD$, por criterio de semejanza AA, $\triangle PBA \sim \triangle PAD$ y $\triangle PBC \sim \triangle PCD$, recordemos que las tangentes $PA$ y $PC$ son iguales.
Por lo tanto,
$\dfrac{BA}{AD} = \dfrac{PB}{PA} = \dfrac{PB}{PC} = \dfrac{BC}{CD}$
$\Rightarrow \dfrac{AB}{BC} = \dfrac{AD}{DC}$.
De acuerdo a la definición 3, $\square ABCD$ es un cuadrilátero armónico.
Proposición 6. Sea $\square ABCD$ un cuadrilátero armónico, entonces $BD$ y las tangentes a $\Gamma$ el circuncírculo de $\square ABCD$, en $A$ y $C$ son concurrentes.
Sean $l_1$ tangente a $\Gamma$ en $A$, $P = l \cap BD$ y $E = AC \cap BD$, por el teorema 2, el haz $A(ABCD)$ es armónico, donde $AA = l_1$, por el teorema 1, $(P, E; D, B) = – 1$.
Análogamente, sea $l_2$ la tangente a $\Gamma$ en $C$ y $Q = l_2 \cap BD$ entonces el haz $C(CBAD)$ es armónico, por lo tanto $(Q, E; D, B) = – 1$.
Por lo tanto, $P = Q$.
$\blacksquare$
Ejemplo
Proposición 7. Sea $\Gamma$ el incírculo de un triángulo $\triangle ABC$, $X$, el punto de contacto de $\Gamma$ con $BC$, $D$ el pie de la altura por $A$ y $M$ el punto medio de $AD$, $N = XM \cap \Gamma$, $N \neq X$ entonces $XN$ es la bisectriz de $\angle BNC$.
Demostración. Sea $L$ el punto al infinito de la recta $AD$, entonces, $M$ y $L$ son conjugados armónicos respecto de $A$ y $D$.

Sea $X’$ el punto diametralmente opuesto a $X$, como $XX’ \parallel AD$, entonces $XX’ \cap AD = L$.
Por el teorema 1, el haz $X(DMAX’)$ es armónico, sea $U = XA \cap \Gamma$, $U \neq X$, entonces $\square XNUX’$ es un cuadrilátero armónico.
Sean $Y$, $Z$ los puntos de tangencia de $\Gamma$ con $CA$ y $AB$ respectivamente, por la proposición 5, $\square XYUZ$ es armónico.
Sea $P = ZY \cap BC$, como $BC$ es tangente a $\Gamma$ en $X$ entonces por la proposición 6, $PU$ es tangente a $\Gamma$.
Como $\square XNUX’$ es armónico, por la proposición 6, $PX$, $PU$, $X’N$ son concurrentes, es decir $X’$, $N$ y $P$ son colineales.
Ya que $XX’$ es diámetro de $\Gamma$, entonces $\angle X’NX = \dfrac{\pi}{2}$, es decir, $NX \perp NP$.
Sabemos que $AX$, $BY$, $CZ$ concurren en el punto de Gergonne $G_e$, entonces por el teorema 2 de la entrada anterior, $P = ZY \cap BC$ es el conjugado armónico de $X$ respecto de $BC$.
Ya que $NX \perp NP$, por el teorema 3 de la entrada anterior, $NX$ es la bisectriz interna de $\angle BNC$.
$\blacksquare$
Más adelante…
En la siguiente entrada hablaremos sobre las simedianas, estas son las reflexiones de la medianas de un triángulo respecto de las bisectrices que pasan por el mismo vértice, con la ayuda de haces armónicos estableceremos algunas propiedades de estas rectas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- En un triángulo $\triangle ABC$, $D$, $E$, $F$, los pies de las alturas por $A$, $B$, $C$, respectivamente, $I_a$, $I_b$, $I_c$ los excentros opuestos a $A$, $B$, $C$ respectivamente, demuestra que $I_aD$, $I_bE$, $I_cF$ son concurrentes.
- $i)$ Dadas tres rectas concurrentes $OA$, $OC$, $OB$, construye el conjugado armónico de $OC$ respecto de $OA$ y $OB$,
$ii)$ Si $(A, B; C, D) = – 1$, $(A, B’; C’, D’) = – 1$, y $AB \neq AB’$, muestra que $BB’$, $CC’$, $DD’$ son concurrentes. - Sea $\square ABCD$ un cuadrilátero convexo, $E = AD \cap BC$, $F = AB \cap CD$, $G = AC \cap BD$, sea $O$ la proyección de $G$ en $FE$, muestra que $\angle AOB = \angle COD$.
- Muestra que las rectas que unen un punto en una circunferencia con los extremos de un cuerda, dividen armónicamente al diámetro perpendicular a dicha cuerda.
- En un triángulo $\triangle ABC$, $A’$ es el punto medio de $BC$, sea $\Gamma$ la circunferencia con diámetro $AA’$, considera $D = \Gamma \cap AB$, $E = \Gamma \cap CA$, $D \neq A \neq E$, y $P$ la intersección de las tangentes a $\Gamma$ en $D$ y $E$, muestra que $PB = PC$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: División armónica.
- Siguiente entrada del curso: Simediana.
- Otros cursos.
Fuentes
- Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 159-166.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 149-161.
- Aref, M. y Wernick, W., Problems and Solutions in Euclidean Geometry. New York: Dover, 2010, pp 178-186.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»