Introducción
En esta entrada definiremos la continuidad de una función, es probable que hayas estudiado antes tal concepto y la manera en que se suele definir de forma intuitiva es mediante la siguiente sentencia: «Si puedes dibujar la función sin levantar el lápiz, entonces es una función continua». Nosotros revisaremos el tema con mayor formalidad, pero notarás que tal enunciado será de ayuda para interpretar la definición.
Definición de continuidad
En palabras sencillas, una función es continua en un punto $x_0$ si el límite en tal punto es igual a evaluar la función en $x_0$.
Definición. Sean $f: A \to \mathbb{R}$ con $A \subset \mathbb{R}$ y $x_0 \in A$. La función $f$ es continua en $x_0$ si para todo $\varepsilon > 0$, existe $\delta > 0$ tal que para todo $x \in A$ que satisface que $0<|x-x_0|< \delta$, entonces se cumple que $|f(x)-f(x_0)|< \varepsilon$.
Observación. Si además $x_0$ es un punto de acumulación de $A$, entonces se dice que $f$ es continua en $x_0$ si $$ \lim_{x \to x_0} f(x) = f(x_0).$$
En la entrada de definición formal de límite se vieron algunos ejemplos de funciones continuas; específicamente se dejaron dos ejercicios como tarea moral que procederemos a probar en esta entrada.
Ejemplo 1. La función $f(x) = c$, es continua en $x_0$ para todo $x_0 \in \mathbb{R}$.
Demostración.
Sea $\varepsilon > 0$. Dado que la función es constante, cualquier valor de delta nos funciona, así consideremos $\delta = 1$.
Si $0<|x-x_0|< \delta$, entonces
\begin{align*}
|f(x)-f(x_0)| & = |c-c|\\
& = 0 \\
& < \varepsilon.
\end{align*}
$$\therefore \lim_{x \to x_0} f(x) = f(x_0).$$
$\square$
Ejemplo 2. La función $f(x) = x$ es continua en $x_0$ para todo $x_0 \in \mathbb{R}$.
Demostración.
Sea $\varepsilon > 0$. Consideremos $\delta = \varepsilon$.
Si $0<|x-x_0|<\delta$, entonces
\begin{align*}
|f(x)-f(x_0)| & = |x-x_0|\\
& < \delta \\
& = \varepsilon.
\end{align*}
$$\therefore \lim_{x \to x_0} f(x) = f(x_0).$$
Antes de revisar el siguiente ejemplo, demostraremos un resultado que nos será muy útil al momento de calcular límites.
Proposición. Sea $f: A \to \mathbb{R}$, entonces
$$\lim_{x \to x_0} f(x) = L \Leftrightarrow \lim_{h \to 0} f(x_0+h) = L.$$
Demostración.
$\Rightarrow]$ Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Sea $\varepsilon > 0$. Existe $\delta > 0 $ tal que si $0 < |x-x_0| < \delta$, entonces $|f(x)-L| < \varepsilon.$
Notemos que si $0 < |h| < \delta$, entonces $0 < |(h+x_0)-x_0| < \delta$. Por lo tanto, $|f(x_0+h)-L| < \varepsilon.$
$$\therefore \lim_{h \to 0} f(x_0+h) = L.$$
$\Leftarrow]$ Supongamos que $$\lim_{h \to 0} f(x_0+h) = L.$$
Sea $\varepsilon>0$. Existe $\delta >0$ tal que si $0<|h|<\delta$, entonces $|f(x_0+h)-L|< \varepsilon.$
Notemos que si $0<|x−x_0|<\delta$, entonces $|f(x_0+(x−x_0))−L|=|f(x)−L|<\varepsilon$.
$$\therefore \lim_{x \to x_0} f(x) = L.$$
$\square$
Ejemplo 3. La función $f(x) = sen(x)$ es continua en $x_0$ para todo $x_0 \in \mathbb{R}.$
Demostración.
Para probar la continuidad de esta función, procederemos a calcular sus límites laterales y emplearemos el hecho de que las funciones seno y coseno son continuas en $x = 0$, lo cual se demostró en esta entrada. Además, usaremos las siguientes identidades trigonométricas:
- $$sen(a+b) = sen(a)cos(b) + cos(a)sen(b).$$
- $$sen(a-b) = sen(a)cos(b) – cos(a)sen(b).$$
Calculando el límite por la derecha, usando la primera identidad y empleando la proposición anterior, tenemos
\begin{align*}
\lim_{x \to x_0^+} sen(x) & = \lim_{h \to 0^+} sen(x_0+h) \\
& = \lim_{h \to 0^+} sen(x_0)cos(h) + cos(x_0)sen(h) \text{, pues $h > 0$} \\
& = sen(x_0)cos(0) + cos(x_0)sen(0) \\
& = sen(x_0).
\end{align*}
Calculando el límite por la izquierda, usando la segunda identidad y empleando la proposición anterior, tenemos
\begin{align*}
\lim_{x \to x_0^-} sen(x) & = \lim_{h \to 0^-} sen(x_0+h) \\
& = \lim_{h \to 0^-} sen(x_0)cos(h) – cos(x_0)sen(h) \text{, pues $h < 0$} \\
& = sen(x_0)cos(0) + cos(x_0)sen(0)\\
& = sen(x_0).
\end{align*}
Como los límites laterales existen y coinciden, se concluye que
$$\lim_{x \to x_0} sen(x) = sen(x_0).$$
Por lo tanto, la función es continua.
$\square$
Propiedades básicas de la continuidad
A continuación revisaremos tres propiedades aritméticas de las funciones continuas.
Teorema. Si $f$ y $g$ son funciones continuas en $x_0$, entonces
- $f+g$ es continua en $x_0$.
- $f \cdot g$ es continua en $x_0$.
- Si además $g(x_0) \neq 0$, entonces $\frac{1}{g}$ es continua en $x_0$.
Demostración.
Como $f$ y $g$ son continuas en $x_0$, entonces
$$\lim_{x \to x_0} f(x) = f(x_0) \quad \text{ y } \quad \lim_{x \to x_0} g(x) = g(x_0).$$
Por las propiedades del límite, tenemos lo siguiente
\begin{align*}
\lim_{x \to x_0} (f + g)(x) & = \lim_{x \to x_0} [f(x) + g(x)] \\
& = \lim_{x \to x_0} f(x) + \lim_{x \to x_0} g(x) \\
& = f(x_0) + g(x_0) \\
& = (f+g)(x_0).
\end{align*}
$$\therefore \lim_{x \to x_0} (f + g)(x) = (f+g)(x_0).$$
Por lo tanto, $f+g$ es continua en $x_0$.
Podemos notar que los incisos siguientes tienen demostraciones análogas ocupando las propiedades demostradas para el límite de una función, por lo cual su prueba se omitirá.
$\square$
Gracias al teorema anterior y los ejemplos vistos, tenemos una gama de funciones continuas, las funciones polinomiales: $p(x) = \alpha_n x^n + \alpha_{n-1} x^{n-1} + \ldots + \alpha_1 x +\alpha_0$.
La siguiente propiedad que veremos hace referencia a la composición de funciones continuas.
Teorema. Si $g$ es continua en $x_0$ y $f$ es continua en $g(x_0)$, entonces la composición de funciones $f \circ g$ es continua en $x_0.$
Demostración.
Queremos probar que $$\lim_{x \to x_0} (f \circ g)(x) = (f \circ g)(x_0)$$
y para demostrarlo procederemos mediante la definición épsilon-delta.
Sea $\varepsilon > 0$.
Como $f$ es continua en $g(x_0)$, existe $\delta’ > 0$ tal que para todo $y$ que cumpla $|y-g(x_0)|< \delta’$, entonces $|f(y)-f(g(x_0))|< \varepsilon$.
Dado que estamos viendo la composición, podemos considerar particularmente $y = g(x)$, de esta manera se tiene que si $|g(x)-g(x_0)|< \delta’$, entonces
\begin{align*}|f(g(x))-f(g(x_0))| <\varepsilon. \tag{1} \end{align*}
Como $g$ es continua en $x_0$, para cualquier valor positivo arbitrario, en este caso consideraremos $\delta’>0$, existe $\delta > 0$ tal que si $0<|x-x_0|<\delta$, entonces
\begin{align*} |g(x)-g(x_0)| < \delta’. \tag{2} \end{align*}
De (1) y (2), se sigue que $$\text{si } 0<|x-x_0|<\delta \Rightarrow |g(x)-g(x_0)| < \delta’ \Rightarrow |f(g(x))-f(g(x_0))| <\varepsilon.$$
Es decir, si $0<|x-x_0|<\delta$, entonces $|f(g(x))-f(g(x_0))| <\varepsilon$.
$\square$
El teorema anterior nos permite extender aún más el almacén de funciones continuas. Por ejemplo, sabemos que $g(x) = x^2+x-10$ es continua en $x_0$ para todo $x_0 \in \mathbb{R}$ y la función $f(x) = sen(x)$ es continua en cualquier punto, particularmente en $g(x_0)$, entonces la composición $(f \circ g) (x) = sen(x^2+x-10)$ también es continua en $x_0$.
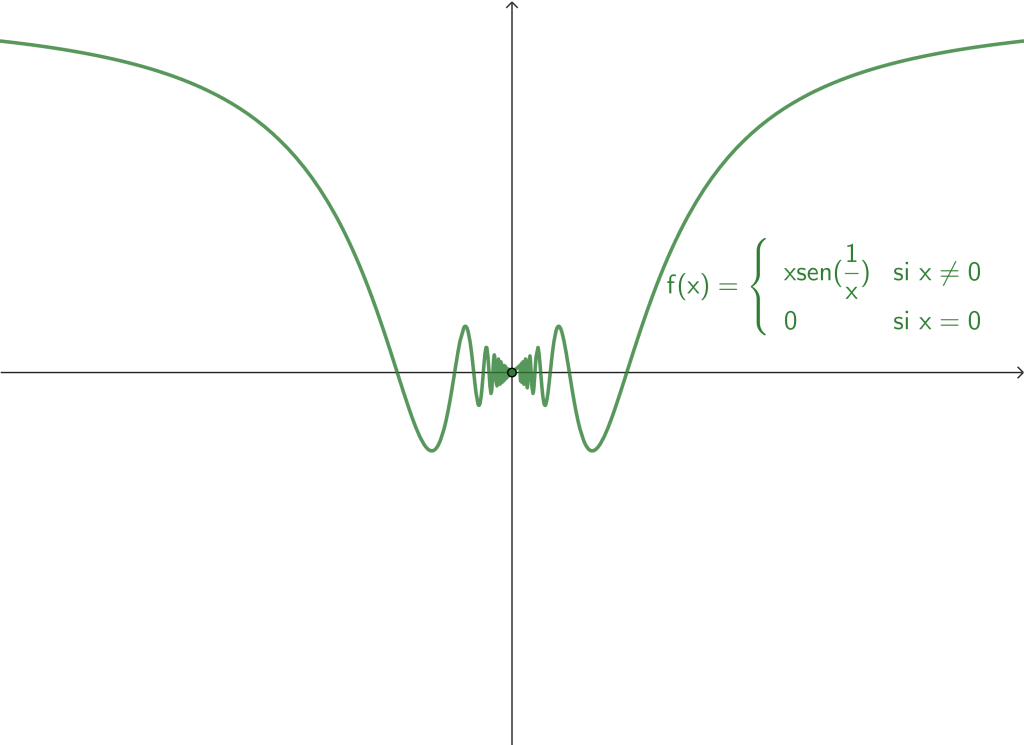
Existen cierto tipo de funciones que no están definidas en algún punto en particular. Por ejemplo $f(x) = xsen(\frac{1}{x})$, no está definida en $x_0=0$ y, por tanto, no puede ser continua en tal punto, pero a partir de ella podemos construir una nueva función que sí sea continua en $x_0=0$. En una entrada anterior, vimos que $$\lim_{x \to 0} xsen \left( \frac{1}{x} \right) = 0.$$
De esta forma, podemos definir una nueva función:
$$f(x) = \begin{cases} xsen(\frac{1}{x}) & \text{si } x \neq 0 \\
0 & \text{si } x = 0. \end{cases}$$
Esta nueva función $f$ es continua en $x_0 = 0$. A este tipo de funciones que podemos convertirlas en funciones continuas en $x_0$ redefiniéndolas en tal punto, se dice que tienen una discontinuidad removible o evitable.
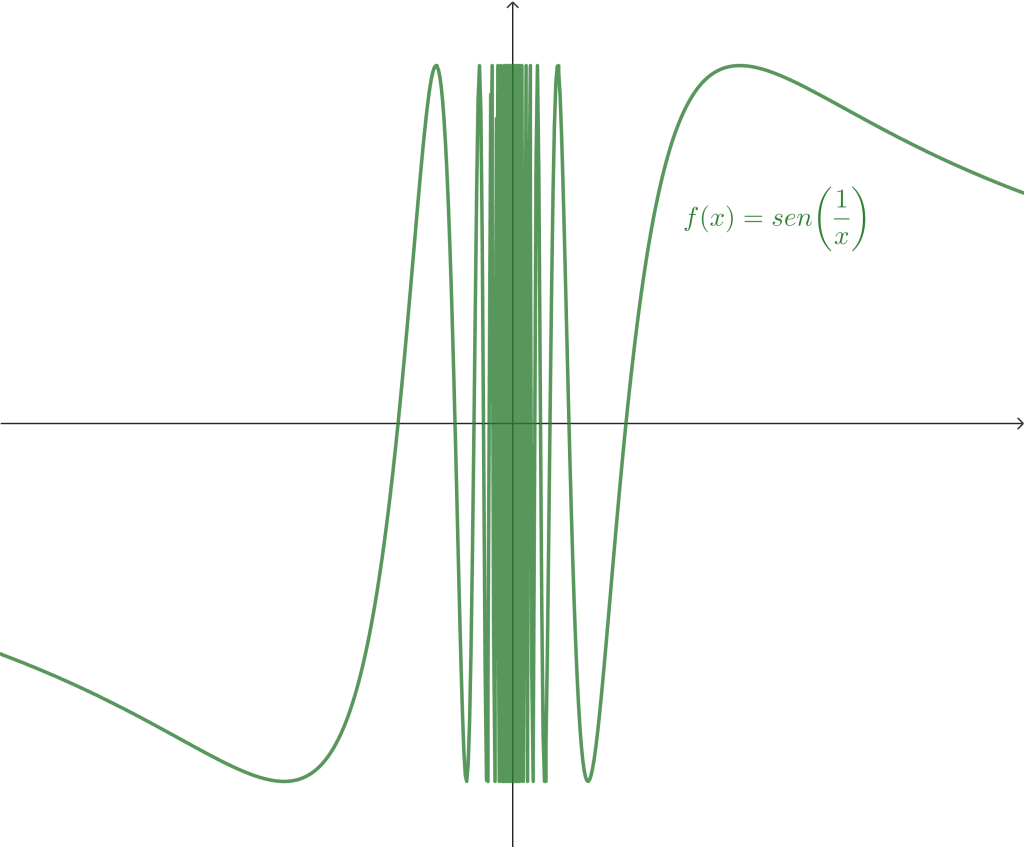
Por otro lado, también hay funciones cuya discontinuidad es no removible. Consideremos la función $f(x) = sen\left( \frac{1}{x} \right)$, revisamos anteriormente que el límite de tal función no existe. Por lo cual, aunque la definiéramos en $x_0$, seguiría siendo discontinua en dicho punto.
Hasta ahora estuvimos empleando la definición de continuidad en un punto, sin embargo, para la mayoría de los ejemplos revisados probamos la continuidad para todo $\mathbb{R}$, puesto que consideramos un $x_0$ arbitrario. Es conveniente tener una definición para la continuidad en un intervalo. Y, como podrás imaginarlo, para que una función sea continua en un intervalo $(a,b)$, se requiere que la función sea continua en cada punto del intervalo (con una pequeña particularidad para intervalos cerrados).
Definición (Continuidad en un intervalo abierto). Si $f$ es continua en todo $x$ con $x \in (a,b)$, se dice que $f$ es continua en el intervalo $(a,b)$.
Definición (Continuidad en un intervalo cerrado). Si $f$ es continua en todo $x$ con $x \in (a,b)$ y se cumple que
$$\lim_{x \to a^+} f(x) = f(a) \quad \text{ y } \quad \lim_{x \to b^-} f(x) = f(b).$$
Entonces se dice que $f$ es continua en el intervalo $[a,b]$.
Terminaremos esta entrada probando un teorema que nos dice que si $f$ es continua en $x_0$ y $f(x_0)$ es mayor a cero (o menor a cero), entonces existe todo un intervalo en el que es mayor a cero (o menor a cero).
Teorema. Supongamos que $f$ es continua en $x_0$ y $f(x_0)>0$. Entonces $f(x) >0$ para todo $x$ en un intervalo que contiene a $x_0$, es decir, existe $\delta > 0$ tal que $f(x) >0$ para todo $x$ tal que $|x-x_0|< \delta$.
De forma análoga, si $f(x_0) <0$, entonces existe $\delta > 0$ tal que $f(x) < 0$ para todo $x$ tal que $|x-x_0|< \delta$.
Demostración.
Supongamos que $f$ es continua en $x_0$ y $f(x_0)>0$, entonces para $\varepsilon = \frac{1}{2}f(x_0) > 0$, existe $\delta>0$ tal que si $|x-x_0|< \delta$, entonces
\begin{gather*}
& |f(x)-f(x_0)|< \frac{1}{2}f(x_0). \\
\Leftrightarrow & -\frac{1}{2}f(x_0) < f(x)-f(x_0) < \frac{1}{2}f(x_0). \\
\Leftrightarrow & -\frac{1}{2}f(x_0) + f(x_0) < f(x) < \frac{1}{2}f(x_0) + f(x_0). \\
\Leftrightarrow & f(x) > \frac{1}{2}f(x_0) > 0.
\end{gather*}
La demostración para cuando $f(x_0)< 0$ es análoga usando $\varepsilon = – \frac{1}{2}f(x_0) > 0.$
$\square$
Más adelante…
Tras revisar las propiedades básicas de las funciones continuas, estamos listos para revisar resultados muy interesantes derivados de la continuidad. En la siguiente entrada revisaremos el popular teorema del valor intermedio, que nos indica que si una función continua en un intervalo $[a,b]$ y que al evaluarla en $a$ toma un valor negativo, $f(a) < 0$, y al evaluarla en $b$ toma un valor positivo, $f(b) > 0$, entonces dicha función necesariamente toma el valor cero, es decir, existe un $x_0$ en el intervalo $[a,b]$ tal que $f(x_0) = 0$. Para probar este resultado, se hará uso del último teorema revisado en esta entrada.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que la función $f(x) = cos(x)$ es continua en cualquier punto $x_0 \in \mathbb{R}$.
- Sea $f: A \to \mathbb{R}$. Prueba que si $f$ es continua en un punto $x_0 \in A$, entonces la función $|f|(x):= |f(x)|$ también es continua en $x_0$. ¿Se cumple el regreso? Es decir, ¿si $|f|$ es continua en $x_0$ entonces $f$ también es continua en tal punto?
- Se dice que una función $f$ es aditiva si $f(x+y) = f(x)+f(y)$ para todo $x$, $y$ en $\mathbb{R}$. Prueba que para una función aditiva $f$ tal que es continua en algún punto $x_0$, entonces es continua en todo su dominio.
- Da un ejemplo de dos funciones $f$ y $g$ discontinuas en $x_0$ tales que la suma $f+g$ sea continua en $x_0.$
- Da un ejemplo de dos funciones $f$ y $g$ discontinuas en $x_0$ tales que el producto $f \cdot g$ sea continuo en $x_0.$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Asíntotas
- Siguiente entrada del curso: Teorema del valor intermedio
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»