Introducción
En esta entrada continuaremos con la demostración del teorema de punto fijo de Banach, enunciado en la sección anterior. Vimos dos ejemplos de contracciones donde generamos una sucesión a partir de cualquier punto del espacio, evaluando la contracción recursivamente. En nuestros ejemplos observamos que la sucesión creada es convergente. ¿Lo será con cualquier contracción? Por lo pronto mostraremos que una sucesión así definida es de Cauchy.
Comencemos comprobándolo para el siguiente caso. Es más general que la primera función vista en Contracciones.
Ejemplo. $f(x)= \alpha x.$
En el espacio euclidiano $\mathbb{R}$ considera $f:\mathbb{R} \to \mathbb{R}$ definida como $f(x)= \alpha x,$ con $\alpha \in (0,1)$ constante. Entonces:
$$d(f(x),f(y))=d(\alpha \, x, \alpha \, y)=|\alpha \, x- \alpha \, y|= \alpha|x-y|=\alpha \, d(x,y)$$
Lo cual prueba que $f$ es contracción.
Veamos ahora que la sucesión generada al evaluar $f,$ partiendo de $x_0 \in \mathbb{R}$ es de Cauchy. Dado $x_0 \in \mathbb{R}$ tenemos:
$x_1:=f(x_0) = \alpha x_0$
$x_2:=f(x_1) = \alpha x_1 = \alpha^2 x_0$
$x_3:=f(x_2) = \alpha x_2 = \alpha^3 x_0$
.
.
.
$x_k:=f(x_{k-1}) = \alpha x_{k-1}= \alpha^k x_0$
Entonces la sucesión está dada por $(\alpha^n x_0)_{n \in \mathbb{N}}.$
A continuación, $ln(x)$ hace referencia al logaritmo natural de $x.$
Sea $\large{\varepsilon} >0$ y sea $N \in \mathbb{N}$ tal que $N > \dfrac{ln \left(\frac{\large{\varepsilon}}{|x_0|} \right)}{ln(\alpha)}.$
Como $\alpha \in (0,1), \, ln(\alpha)< 0.$ Se sigue que:
\begin{align*}
& &N \, ln(\alpha) &< ln \left(\frac{\varepsilon}{|x_0|} \right) \\
&\Rightarrow \, &exp \left(ln \left(\alpha^N \right) \right) &< exp \left( ln \left( \frac{\varepsilon}{|x_0|} \right) \right) \\
&\Rightarrow \, &\alpha^N&< \frac{\varepsilon}{|x_0|}
\end{align*}
La última desigualdad se usará en las siguientes líneas.
Sean $n,m \geq N.$ Supón sin pérdida de generalidad que $n \leq m$ entonces $\alpha^n \geq \alpha^m \geq 0 .$ Tenemos:
\begin{align*}
d(x_n,x_m) &= |x_n-x_m|\\
&=|\alpha^n x_0 \, – \, \alpha ^m x_0|\\
&= |\alpha ^n – \alpha^m||x_0|\\
&\leq \alpha ^n|x_0| \\
&\leq\alpha ^N |x_0| \\
&\leq \frac{\varepsilon}{|x_0|}|x_0| \\
&= \varepsilon
\end{align*}
Por lo tanto la sucesión $(\alpha^n x_0)_{n \in \mathbb{N}} \,$ es de Cauchy.
Pasemos a demostrar el caso general:
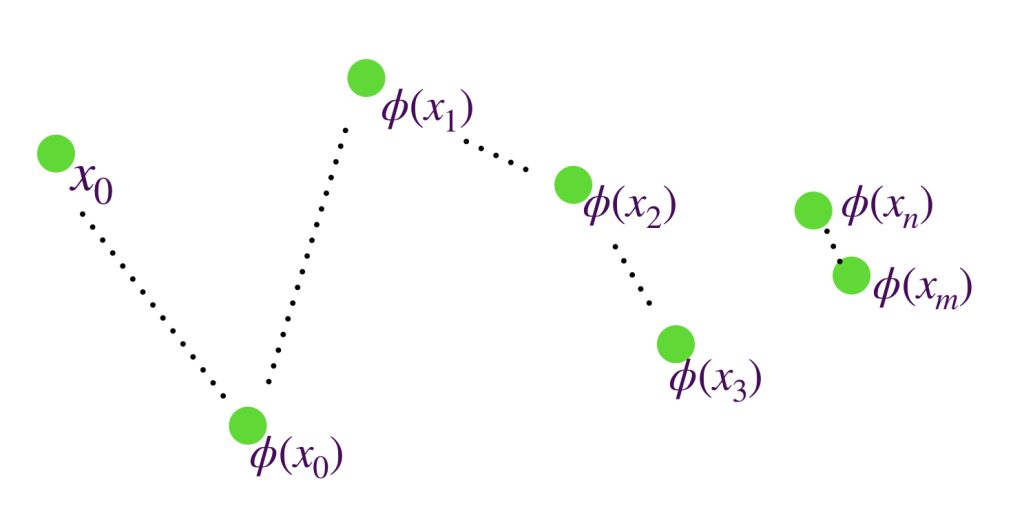
Proposición: Sea $(X,d)$ un espacio métrico, $\phi : X \to X$ una contracción con constante $\alpha \in (0,1)$ y sea $x_0 \in X.$ Entonces la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy en $X.$
Demostración:
Comencemos con un análisis entre distancias de los primeros pares de puntos de la sucesión.
\begin{align*}
&d(x_1,x_2) = d(\phi(x_0),\phi(x_1)) &\leq \alpha d(x_0,x_1) \\
&d(x_2,x_3)=d(\phi(x_1),\phi(x_2)) \leq \alpha d(x_1,x_2) \leq \alpha (\alpha d(x_0,x_1)) &= \alpha^2 d(x_0,x_1)\\
&d(x_3,x_4) =d(\phi(x_2), \phi(x_3)) \leq \alpha d(x_2,x_3) \leq \alpha(\alpha^2d(x_0,x_1)) &= \alpha^3d(x_0,x_1)
\end{align*}
Por inducción sobre $n$ podemos concluir que la distancia entre cualquier punto de la sucesión y el siguiente está limitada por
\begin{equation}
d(x_n,x_{n+1})=d(x_n, \phi(x_n)) \leq \alpha^n d(x_0,x_1)
\end{equation}
Pasemos a probar que $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy en $X.$
Sea $\varepsilon>0$ y $N \in \mathbb{N}$ tal que $N \geq \, \dfrac{ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right)}{ln (\alpha)}.$ Entonces si $n > N:$
\begin{align*}
& &n &> \dfrac{ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right)}{ln (\alpha)} \\
&\Rightarrow & n \, ln (\alpha) &< ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \\
&\Rightarrow & ln (\alpha^n) &< ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \\
&\Rightarrow & exp(ln (\alpha^n)) &< exp \left(ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \right) \\
&\Rightarrow & \alpha^n &< \dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}
\end{align*}
\begin{equation}
\Rightarrow \, \dfrac{\alpha^n}{1- \alpha} d(x_0,x_1) < \large{\varepsilon}
\end{equation}
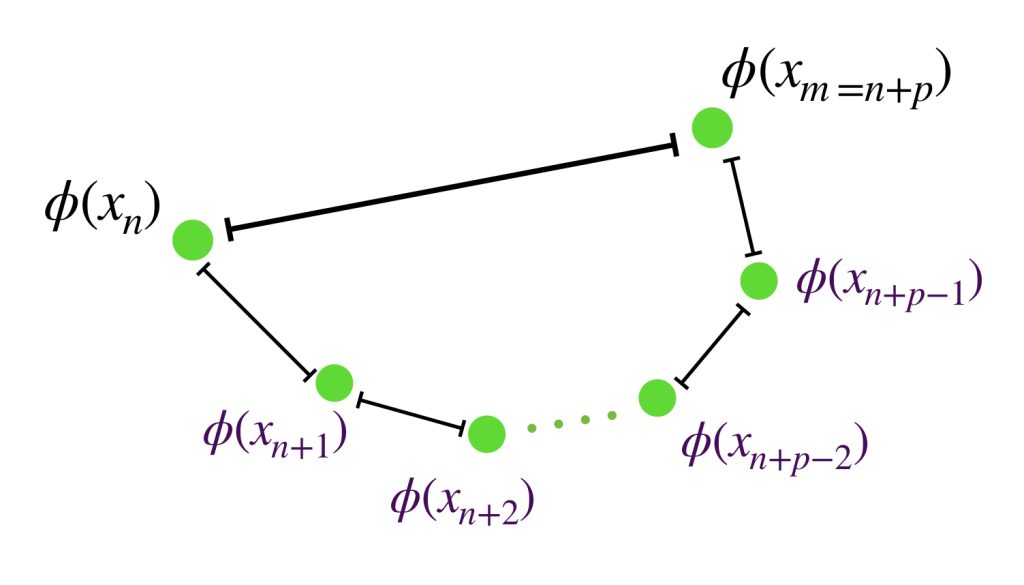
Sean $n,m \in \mathbb{N} \,$ tales que $n,m > N.$ Sin pérdida de generalidad supón que $m \geq n.$ Entonces $m \, = \, n+p$ para algún $p \in \mathbb{N}.$ A partir de la desigualdad del triángulo sabemos que la distancia entre el punto $x_n$ y el punto $x_m=x_{n+p}$ es menor igual que la suma de las distancias de todos los puntos de la sucesión que están entre ellos dos.
Se sigue:
\begin{align*}
d(x_n,x_m) &= d(x_n,x_{n+p})\\
&\leq d(x_n,x_{n+1}) +d(x_{n+1},x_{n+2}) …+ d(x_{n+p-2},x_{n+p-1})+d(x_{n+p-1},x_{n+p})\\
&\leq \alpha^n d(x_0,x_1) +\alpha^{n+1} d(x_0,x_1)+…+ \alpha^{n+p-2} d(x_0,x_1)+\alpha^{n+p-1} d(x_0,x_1) \text{ por ec. $(1)$}\\
&= (\alpha^n +\alpha^{n+1} +…+ \alpha^{n+p-2} +\alpha^{n+p-1} ) \, d(x_0,x_1) \\
&=\alpha^n \, (1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}) \, d(x_0,x_1)
\end{align*}
Nota que $1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}$ es la suma de los primeros términos de la serie $\sum_{k=0}^{\infty}\, \alpha^k.$ Probablemente has visto en otros cursos que ésta es una serie convergente y que $\sum_{k=0}^{\infty}\, \alpha^k \, = \dfrac{1}{1-\alpha}$, pues $|\alpha|<1$. Puedes consultarlo en la sección Cálculo Diferencial e Integral II: Series Geométricas. Entonces:
$$1+\alpha +…+\alpha^{p-2}+\alpha^{p-1} \leq \sum_{k=0}^{\infty}\, \alpha^k \, = \dfrac{1}{1-\alpha}$$
De modo que
\begin{align*}
\alpha^n \, (1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}) \, d(x_0,x_1) &\leq \alpha^n \, \sum_{k=0}^{\infty}\, \alpha^k \, d(x_0,x_1) \\
&\leq \alpha^n \frac{1}{1- \alpha} \, d(x_0,x_1)\\
&< \varepsilon \text{ por ec. (2)}
\end{align*}
Por lo tanto $d(x_n,x_m) < \varepsilon \, $ lo cual demuestra que $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es una sucesión de Cauchy.
Más adelante
Terminaremos con la prueba del teorema de punto fijo de Banach. Mostraremos condiciones bajo las cuales esta sucesión de Cauchy es convergente y cómo aproximar la sucesión al punto de convergencia.
Tarea moral
- Da un ejemplo de un espacio métrico completo y una función $\phi: X \to X$ que satisface que para cada $x,y \in X$ con $x \neq y, \, d(\phi(x), \phi(y)) < d(x,y)$ y que no tiene ningún punto fijo.
- Prueba que si $X$ es un espacio métrico compacto y $\phi: X \to X$ satisface que para cada $x,y \in X$ con $x \neq y, \, d(\phi(x), \phi(y)) < d(x,y)$ entonces $\phi$ tiene un único punto fijo.