Introducción
En esta entrada y en otras subsecuentes, trataremos el tema de series aplicado a la resolución de problemas matemáticos. Recordemos que en entradas anteriores ya se estudiaron los conceptos de sucesiones. Para esta entrada aprovecharemos lo que hemos aprendido de sucesiones geométricas.
Series geométricas
Si consideramos una sucesión geométrica $\{a_i\}_{i\in\mathbb{N}}$, recordemos que se cumple que existe una razón $r$ de tal manera que $a_n=ra_{n-1}$, expresado en el primer término, tenemos que $a_n=r^{n}a_0$. Ahora bien, nos interesará saber o conocer las suma de los elementos de una sucesión geométrica. A esta suma se le conoce como serie geométrica y puede realizarse considerando una cantidad finita de elementos de la sucesión, así como una cantidad infinita de elementos de la sucesión.
Si queremos obtener la serie geométrica de los primeros $n+1$ elementos de la sucesión $\{a_i\}_{i\in\mathbb{N}}$, tenemos lo siguiente
\begin{equation*}
\sum_{i=0}^n a_i=a_0+a_1+a_2 +a_3+\ldots+a_n.
\end{equation*}
Al multiplicar ambos lados de la igualdad por la razón de la sucesión tenemos que
\begin{align}
\sum_{i=0}^n a_i&=a_0+a_1+a_2 +a_3+\ldots+a_n\\
r\sum_{i=0}^n a_i&=ra_0+ra_1+ra_2 +ra_3+\ldots+ra_n\\
&=a_1+a_2+\ldots+a_{n+1}
\end{align*}
Y si calculamos $r\sum_{i=0}^n a_i-\sum_{i=0}^n a_i$, se cancelan todos los términos excepto el último de la primer suma, y el primero de la segunda. Obtenemos entonces:
\begin{align*}
r\sum_{i=0}^n a_i-\sum_{i=0}^n a_i&=a_{n+1}-a_0.
\end{align*}
Así,
\begin{equation*}
\sum_{i=0}^na_i=\frac{a_{n+1}-a_0}{r-1}=a_0\frac{r^{n+1}-1}{r-1}.
\end{equation*}
Ahora bien, si tenemos la sucesión geométrica $\{a_i\}_{i\in\mathbb{N}}$ y queremos calcular la serie infinita de todos sus elementos basta con que calculemos el límite cuando $n\to \infty$ tiende a infinito de $$\sum_{i=0}^na_i=a_0\frac{r^{n+1}-1}{r-1}.$$
Supogamos que $a_0\neq 0$, pues en otro caso la suma de los términos es igual a $0$. Si $|r|>1$, el numerador diverge y por lo tanto la serie también. Cuando $r=1$, la serie diverge pues cada sumando es igual a $a_0\neq 0$. Cuando $r=-1$, tenemos una serie de términos alternante que no converge, pues es, iteradamente, $a_0,0,a_0,0,\ldots$.
Por otro lado, si $|r|<1$, entonces $r^{n+1}\to 0$. En este caso, la serie converge a $\frac{a_0}{1-r}$.
Aplicación de series geométricas a áreas
Si consideramos la sucesión $\{x^i\}_{i\in\mathbb{N}}$ tenemos que dicha sucesión está dada por $\left\{1, x, x^2, x^3,\ldots\right\}$ la sucesión es geométrica, dado que la razón es $r=x$.
De acuerdo al análisis que hicimos arriba, la serie geométrica finita está dada por
\begin{equation*}
\sum_{i=0}^n x^i=(1)\frac{x^{n+1}-1}{x-1}=\frac{1-x^{n+1}}{1-x}
\end{equation*}
A partir de aquí deducimos que la serie geométrica infinita está dada por
\begin{equation*}
\sum_{i=0}^{\infty} x^i=\lim_{n\to\infty}\frac{1-x^{n+1}}{1-x}=\frac{1}{1-x}
\end{equation*}
solo si $|x|< 1$. En otro caso, la serie diverge.
$\square$
Un problema aplicado a la geometría
Consideremos la siguiente figura, en donde $\triangle ABC$ es un triángulo equilatero y $OA=16$. 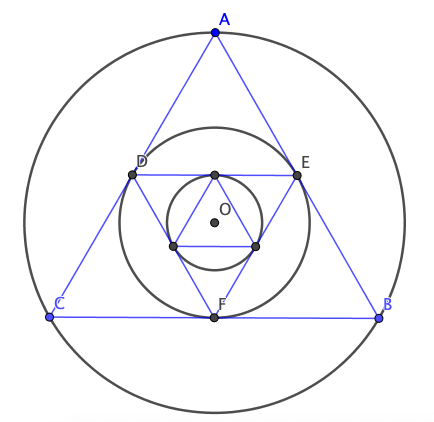
Imaginemos que la figura continúa internamente de manera infinita, resultando en una cantidad infinita de triángulos, todos ellos equiláteros. ¿Cuál sería la suma de las áreas de todos los triángulos?
Para ello, primero tendríamos que ver el área de cada triángulo como elemento de una sucesión, la cual parece que será geométrica.
Comencemos calculando el área del $\triangle ABC$. Para ello tenemos que determinar el valor de la altura. Notemos que $CE$ es altura del triángulo, a su vez, $CE=OC+OE$. Como $OC$ es radio de la circunferencia, tenemos que $OC=16$. Sólo falta determinar el valor del segmento $OE$.
Si nos fijamos en $\triangle AOE$, tenemos que es un triángulo rectángulo, además que $AO$ es bisectriz del $\angle A$, así que $\angle OAE=30^o$. Como $\sin30^o=OE/16=1/2$ tenemos entonces que $OE=8$.
Por lo anterior, tenemos que que la altura del $\triangle ABC$ está dada por $h=24$. De una manera similar podemos calcular la base del triángulo, la cual está dada por $b=16\sqrt{3}$. Así, el área del $\triangle ABC$ es $A_0=192\sqrt{3}$.
El área del triángulo inscrito en el $\triangle ABC$ es la cuarta parte de $A_0$, es decir $A_1=\frac{1}{4}A_0$. De manera sucesiva $A_2=\frac{1}{4}A_1$, $A_3=\frac{1}{4}A_2, \ldots$.
Si nos fijamos en la sucesión de las áreas de los triángulos$\{A_i\}_{i\in\mathbb{N}$ tenemos que es geométrica de razón $r=1/4$.
De esta forma, la suma de las áreas de todos los triángulos es una serie geométrica dada por
\begin{align*}
\sum_{i=0}^{\infty} A_i&=\lim_{x\to\infty}(192\sqrt{3})\frac{1-(1/4)^{n+1}}{1-(1/4)}\\
&=(192\sqrt{3})\frac{1}{1-(1/4)}=(192\sqrt{3})(4/3)\\
&=256\sqrt{3}
\end{align*}
$\square$
Aplicación de series geométricas a números perfectos
Un número entero positivo $n$ se dice que es perfecto si la suma de sus divisores sin incluir al mismo $n$ da como resultado $n$. Por ejemplo, el número $6$ es un número perfecto ya que sus divisores sin incluir al mismo $6$ son $1, 2, 3$ y su suma $1+2+3=6$.
Ahora veamos un problema que relaciona a los números perfectos y a las series geométricas.
Problema: Sea $n=2^{p-1}(2^p-1)$, donde $2^p-1$ es primo. Prueba que $n$ es un número perfecto.
Solución: Tenemos que todos los divisores de $n$ sin contar al mismo $n$ están conformados por la unión de las siguientes dos sucesiones finitas.
\begin{align*}
&\{2^i\}_{i=0}^{p-1}=1, 2, 2^2,…,2^{p-1}\\
&\{(2^p-1)2^i\}_{i=0}^{p-2}=(2^p-1), 2^2(2^p-1), 2^3(2^p-1),…, 2^{p-2}(2^p-1)
\end{align*}
Si consideramos la suma de los elementos de cada sucesión
\begin{align*}
&\sum_{i=0}^{p-1}2^i=\frac{2^p-1}{2-1}=2^p-1\\
&\sum_{i=0}^{p-2}2^i(2^p-1)=(2^p-1)\frac{2^p-1}{2-1}=(2^p-1)(2^{p-1}-1)
\end{align*}
Así la suma de todos los divisores de $n$ sin incluir al propio $n$ es
\begin{align*}
(2^p-1)+(2^p-1)(2^{p-1}-1)&=(2^p-1)(1+2^{p-1}-1)\\
&=2^{p-1}(2^p-1)\\
&=n.
\end{align*}
Por lo tanto, tenemos que $n$ es un número perfecto.
$\square$
Otro problema interesante
Problema: Una sucesión está definida por $a_1=2$ y $a_n=3a_{n-1}+1$, encuentra el valor de la suma $$a_1+a_2+a_3+\ldots+a_n.$$
Solución: Notemos que la sucesión que nos dan no es geométrica, dado que no es posible encontrar un número $r$ que funcione como razón. Así que busquemos un patrón que aparezca al realizar las primeras sumas.
\begin{align*}
a_1&=2\\
a_2&=3a_1+1\\
&=3(2)+1\\
a_3&=3a_2+1\\
&=3(3(2)+1)+1\\
&=3^2(2)+3+1\\
a_4&=3a_3+1\\
&=3(3^2(2)+3+1)+1\\
&=3^3(2)+3^2+3+1\\
a_5&=3a_4+1\\
&=3(3^3(2)+3^2+3+1)\\
&=3^4(2)+3^3+3^2+3+1.
\end{align*}
De manera sucesiva, podemos conjeturar y mostrar por inducción que
\begin{align*}
a_n&=3^{n-1}(2)+3^{n-2}+\ldots+3+1\\
&=3^{n-1}(2)+\frac{3^{n-1}-1}{2}\\
&=\frac{5\cdot 3^{n-1}-1}{2}.
\end{align*}
Así que
\begin{align*}
\sum_{i=1}^na_i&=\sum_{i=1}^n \frac{5\cdot 3^{i-1}-1}{2}\\
&=\frac{1}{2}\sum_{i=1}^n 5\cdot 3^{i-1}-1\\
&=\frac{1}{2}\left(5\cdot \frac{3^n-1}{2} – n\right).
\end{align*}
$\square$
Más problemas
Puedes encontrar más problemas de series geométricas en la sección 5.2 del libro Problem Solving through Problems de Loren Larson.
