Introducción
La regla de la cadena permite derivar funciones que dependen de otras variables, por otro lado el plano tangente es la mejor aproximación lineal de una superficie en un punto.
Caso particular de la regla de la cadena
Supongamos que $C:\mathbb{R}\rightarrow\mathbb{R}^{3}$ es una trayectoria diferenciable y $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$.
Sea $h(t)$=$f(x(t), y(t), z(t))$ donde $c(t)$=$(x(t),y(t), z(t))$.
Entonces
$$\displaystyle\frac{\partial{h}}{\partial{t}} = \displaystyle\frac{\partial{f}}{\partial{x}}\cdot \frac{\partial{x}}{\partial{t}}+\frac{\partial{f}}{\partial{y}}\cdot
\frac{\partial{y}}{\partial{t}}+\frac{\partial{f}}{\partial{z}}\cdot
\frac{\partial{z}}{\partial{t}}$$
Esto es:
$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\nabla{f(c(t))}\cdot
{c'(t)}$, ~donde $c'(t)$=$((x'(t), y'(t), z'(t))$
Demostración. Por definición
$\displaystyle\frac{\partial{h}}{\partial{t}}(t_{0})$=$\displaystyle\lim_{t\rightarrow0}\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$
Sumando y restando tenemos que
$\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$=$\displaystyle\frac{f(c(t))-f(c(t_{0}))}{t-t_{0}}$=$\displaystyle\frac{f(x(t), y(t), z(t)) – f(x(t_{0}), y(t_{0}), z(t_{0}))}{t-t_{0}}$=
=$\frac{f(x(t), y(t), z(t))~-~f(x(t_{0}), y(t),
z(t))~+~f(x(t_{0}), y(t), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t))~+~f(x(t_{0}), y(t_{0}), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t_{0}))}{t-t_{0}}$…$\ast$
Aplicando el Teorema del valor medio $\textbf{(T.V.M.)}$
$f(~x(t),~y(t),~z(t))-f(~x(t_{0}),~y(t),~z(t))=\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~(x(t)-x(t_{0}))$
$f(~x(t_{0}),~y(t),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t))=\displaystyle\frac{\partial{f}}{\partial{y}}~(x(t),~ d, ~z(t))~(y(t)-y(t_{0}))$
$f(~x(t_{0}),~y(t_{0}),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t_{0}))=\displaystyle\frac{\partial{f}}{\partial{z}}(~x(t),~y(t),~e)~(z(t)-z(t_{0}))$
$\therefore$$\ast$=$\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~\displaystyle\frac{x(t)-x(t_{0})}{t-t_{0}}+\displaystyle\frac{\partial{f}}{\partial{y}}~(~x(t),~d,~z(t))~\displaystyle\frac{y(t)-y(t_{0})}{t-t_{0}}$+
$+\displaystyle\frac{\partial{f}}{\partial{z}}~(~x(t),~y(t),~e))~\displaystyle\frac{z(t)-z(t_{0})}{t-t_{0}}$
Tomando $\displaystyle\lim_{t\rightarrow{t_{0}}}$ y por la continuidad de las parciales
$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\displaystyle\frac{\partial{f}}{\partial{x}}~\frac{\partial{x}}{\partial{t}}+ \displaystyle\frac{\partial{f}}{\partial{y}}~\frac{\partial{y}}{\partial{t}}+\displaystyle\frac{\partial{f}}{\partial{z}}~\frac{\partial{z}}{\partial{t}}$
Ejemplos: Caso particular de la regla de la cadena
Ejemplo. Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+3y^{2}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$
Solución. En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=2x\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=2e^{t}\cdot e^{t}=2e^{2t}$$
$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (\cos(t))}{dt}=6y\left|{(e^{t},\cos(t))}\cdot (-sen(t))\right.=6 cos(t) \cdot (- sen(t))$$
por lo tanto
$$h'(t)=2e^{2t}-6\cos(t)\cdot (sen(t))$$
Ejemplo. Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=xy$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$
Solución. En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (xy)}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=y\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=\cos(t)\cdot e^{t}$$
$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (xy)}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (cos(t))}{dt}=x\left|{(e^{t},cos(t))}\cdot (-sen(t))\right.=e^{t}\cdot (-sen(t))$$
por lo tanto
$$h'(t)=\cos(t)e^{t}-e^{t}\cdot sen(t)$$
Ejemplo.Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=e^{xy}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(3t^{2},t^{3})$
Solución. En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial x}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (3t^{2})}{dt}=ye^{xy}\left|{(3t^{2},t^{3})}\cdot 6t\right.=t^{3}e^{3t^{5}}6t=6t^{4}e^{3t^{5}}$$
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial y}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (t^{3})}{dt}=xe^{xy}\left|{(3t^{2},t^{3})}\cdot 3t^{2}\right.=3t^{2}e^{3t^{5}}3t^{2}=9t^{4}e^{3t^{5}}$$
por lo tanto
$$h'(t)=6t^{4}e^{3t^{5}}+9t^{4}e^{3t^{5}}=15t^{4}e^{3t^{5}}$$
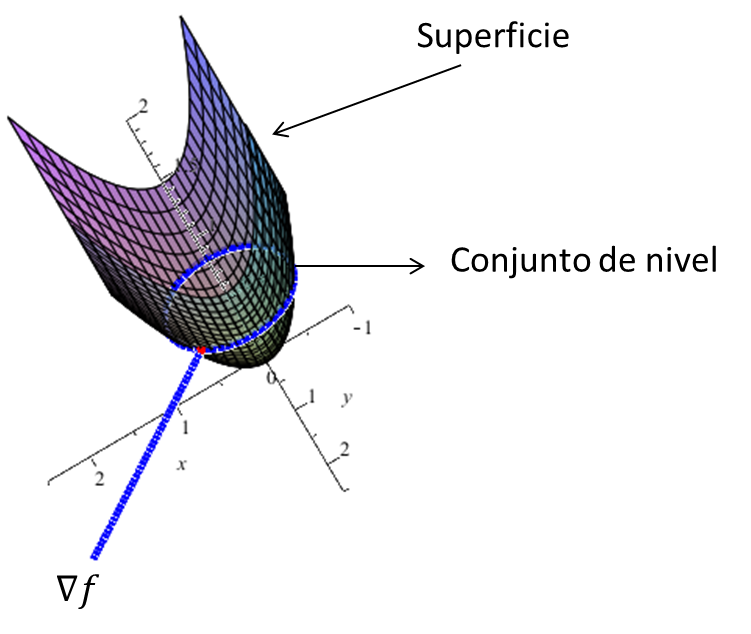
Teorema 1. El gradiente es normal a las superficies de nivel. Sea $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ una aplicación $C^{1}$ y sea
$(x_{0},y_{0},z_{0})$ un punto sobre la superficie de nivel $S$ definida por $f(x,y,z)$=$k$, $k$=$cte$. Entonces $\nabla{f}(x_{0},~y_{0},~z_{0})$ es normal a la superficie de nivel en el siguiente sentido: si $v$ es el vector tangente en $t$=$t_{0}$ de
una trayectoria $c(t)$ con $c(t_{0})$=$(x_{0},~y_{0},~z_{0})$ Entonces $\nabla{f}\cdot {v}$=$0$
que se puede escribir como
$$\left(\frac{\partial f}{\partial x}(x(t),y(t)z(t)),\frac{\partial f}{\partial y}(x(t),y(t)z(t)),\frac{\partial f}{\partial z}(x(t),y(t)z(t))\right)\cdot\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)=0$$
en $t=t_{0}$
$$\nabla f(x(0),y(0),z(0))\cdot c'(t_{0})=0$$
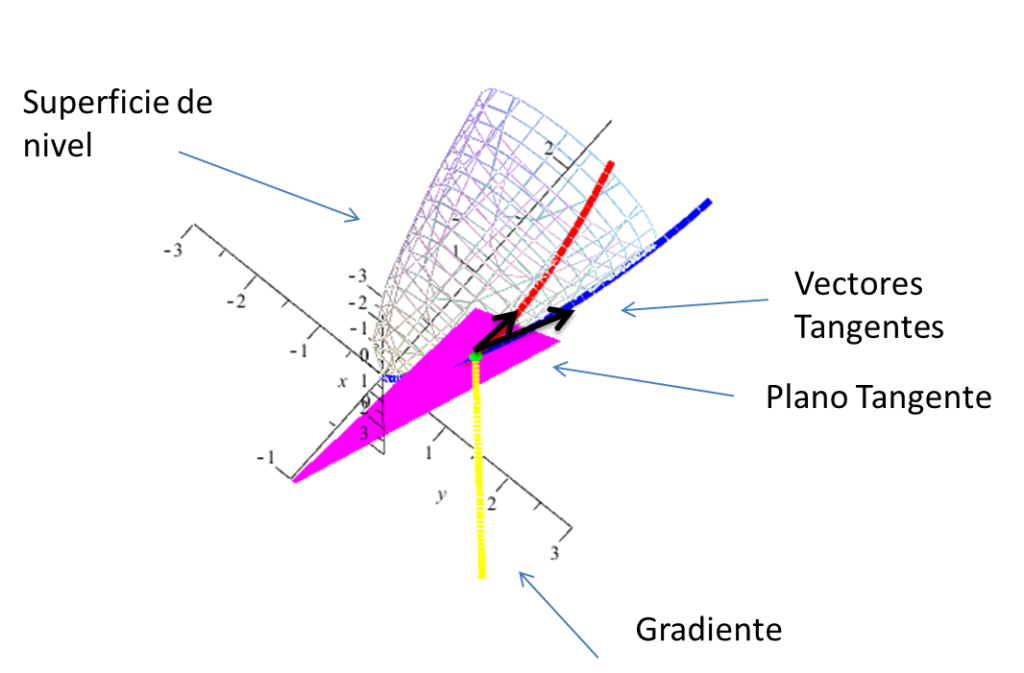
Plano Tangente
Sea $f:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}$ una función diferenciable definida en A, y sea
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c \right\}$$
una superficie de nivel de f y $\hat{x}_{0}=(x_{0},y_{0},z_{0})$ un punto de ella. Considere además, una curva
$$\alpha(t)=(x(t),y(t),z(t))$$
y una curva
$$\beta(t)=(x_{1}(t),y_{1}(t),z_{1}(t))$$
que pasen por $\hat{x}_{0}$ con $t\in[a,b]$ en ambos casos y tanto $\alpha$ como $\beta$ diferenciables, se tiene entonces $$(f\circ\alpha)'(t)=f'(\alpha(t))\alpha'(t)=\nabla f(\alpha(t))\cdot \alpha'(t)=0$$ $$(f\circ\beta)'(t)=f'(\beta(t))\beta'(t)=\nabla f(\beta(t))\cdot \beta'(t)=0$$ pues el gradiente $\nabla f(\hat{x}{0})$ en ambos casos es ortogonal tanto al vector $\alpha'(t_{0})$ como al vector $\beta'(t_{0})$ en el punto $\hat{x_{0}}=\alpha(t_{0})=\beta(t_{0})$
Si $\nabla f(\hat{x}{0})\neq 0$, entonces las tangentes a las curvas $\alpha, \beta$ sobre S que pasan por $\hat{x}{0}$
están contenidas en un mismo plano; por lo que el plano tangente a
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c \right\}$$ se define
Definición. El plano tangente a S en $\hat{x}{0}$ se define $$P=\left\{\hat{x}~|~\nabla f(\hat{x}_{0})\cdot (\hat{x}-\hat{x}_{0})=0 \right\}$$
Ejemplo. Hallar el plano tangente a la superficie
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~\frac{x^{2}}{4}-\frac{y^{2}}{9}+z^{2}=1 \right\}$$
en el punto $(2,3,1)$
Solución. En este caso el gradiente es
$$\nabla f(x,y,z)=\left(\frac{x}{2},-\frac{2}{9}y,2z\right)$$
en el punto $(2,3,1)$ es
$$\nabla f(2,3,1)=\left(1,-\frac{2}{3},2\right)$$
Por tanto la ecuación del plano tangente es
$$\left(1,-\frac{2}{3},2\right)\cdot (x-1,y-3,z-1)=0$$
es decir
$$3x-2y+6z-6=0$$
Mas adelante
En la siguiente entrada estudiaremos el tema de derivadas de orden superior, el cual, trata de estudiar qué ocurre cuando derivamos una función más de una vez, y cómo esas derivadas adicionales nos dan información más profunda sobre el comportamiento de la función.
Tarea Moral
1.- Verifica la regla de la cadena para $f(x,y)=(x^2+y^2) log \sqrt{x^2+y^2}$ y la trayectoria $c(t)=(e^t,e^{-t})$
2.- Aplica la regla de la cadena para $f(x,y)=x exp(x^2+y^2)$ y $c(t)=(t,-t)$
3.- Sea la superficie $S=\left\{(x,y,z) \in \mathbb{R}^3 ~|~ x^2+y^2+(z-6)^2=9 \right\}$ calcula el plano tangente en $(4,-1,2)$
4.- Sea la superficie $S=\left\{(x,y,z) \in \mathbb{R}^3 ~|~ \sqrt {x^2+y^2+z^2} =5 \right\}$ calcula el plano tangente en $(0,2,-6)$
5.- Calcula la ecuación del plano tangente a la superficie definida por $S=\left\{(x,y,z) \in \mathbb{R}^{3} ~|~ 3xy+z^2 =4 \right\}$ calcula el plano tangente en $(1,1,1)$
Enlaces
El siguiente enlace muestra la gráfica de el hiperboloide mostrado anteriormente como ejemplo $S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~\frac{x^{2}}{4}-\frac{y^{2}}{9}+z^{2}=1 \right\}$ y su plano tangente en el punto $(2,3,1)$. Puedes modificar la superficie por la que tú quieras para seguir observando este concepto.
https://www.geogebra.org/calculator/rmpbz7ft
Se muestra otra gráfica con su respectivo plano tangente en un punto, en esta ocasión el plano tangente va variando su inclinación dependiendo del punto.