Derivadas Parciales de Orden Superior

Si $f$ es una función de doas variables $x,y$ $\Rightarrow$ $\displaystyle\frac{\partial f}{\partial x}, \displaystyle\frac{\partial f}{\partial y}$ son funciones de las mismas variables, cuando derivamos $\displaystyle\frac{\partial f}{\partial x}$ y $ \displaystyle\frac{\partial f}{\partial y}$ obtenemos las derivadas parciales de segundo orden, las derivadas de $\displaystyle\frac{\partial f}{\partial x}$ están definidas por:

$$\displaystyle\frac{\partial^{2}f}{\partial x^{2}}(x,y)=\displaystyle\lim_{h\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x+h,y)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{h}}$$

$$\displaystyle\frac{\partial^{2}f}{\partial y \partial x}(x,y)=\displaystyle\lim_{k\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x,y+k)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{k}}$$

Si $f$ es una función de dos variables entonces hay cuatro derivadas parciales de segundo orden.

Consideremos las diferentes notaciones para las derivadas parciales:

$$f_{1,1}=\displaystyle\frac{\partial^{2}f}{\partial x^{2}}=f_{xx}$$

$$f_{1,2}=\displaystyle\frac{\partial^{2}f}{\partial y \partial x}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial x}\bigg)=f_{xy}$$

$$f_{2,1}=\displaystyle\frac{\partial^{2}f}{\partial x \partial y}=\frac{\partial}{\partial x}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yx}$$

$$f_{2,2}=\displaystyle\frac{\partial^{2}f}{\partial y^{2}}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yy}$$

Ejemplo. $z=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$ hallar $\displaystyle\frac{\partial z}{\partial x}, \displaystyle\frac{\partial z}{\partial y},\displaystyle\frac{\partial^{2} z}{\partial x^{2}},\displaystyle\frac{\partial^{2}z}{\partial x \partial y},\displaystyle\frac{\partial^{2}z}{\partial y \partial x},\displaystyle\frac{\partial^{2} z}{\partial y^{2}}$

$$\displaystyle\frac{\partial z}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$

$$\displaystyle\frac{\partial z}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$

$$\displaystyle\frac{\partial^{2} z}{\partial x^{2}}=6x+6y-4y^{2}$$

$$\displaystyle\frac{\partial^{2} z}{\partial y^{2}}=-4x^{2}-12y^{2}$$

$$\displaystyle\frac{\partial^{2}z}{\partial y \partial x}=6x-8xy+3$$

$$\displaystyle\frac{\partial^{2}z}{\partial x \partial y}=6x-8xy+3$$

Teorema 1.Teorema de schwarz

Sea $f:A\subset \mathbb{R}^{2}\rightarrow\mathbb{R}$ una función definida en el abierto A de $\mathbb{R}^{2}$. Si las derivadas parciales

$$\frac{\partial^{2} f}{\partial y\partial x}~y~\frac{\partial^{2} f}{\partial x\partial y}$$

existen y son continuas en $A$, entonces

$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} f}{\partial x\partial y}$$

Demostración. Sea

$\displaystyle{M=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-f(x,y+h_{2})+f(x,y)}$ y definimos $$\varphi(x)=f(x,y+h_{2})-f(x,y)$$de manera que
$$\varphi(x+h_{1})-\varphi(x)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$

Aplicando el TVM a $\varphi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\theta~\in~(x,x+h_{1})$ tal que

$$\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}$$

por otro lado
$$\varphi'(x)=\frac{\partial f}{\partial x}(x,y+h_{2})-\frac{\partial f}{\partial x}(x,y)$$
por lo tanto
$$\varphi'(\theta)=\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)$$
tenemos entonces que

$$M=\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}$$
Consideremos ahora $\displaystyle{\psi(y)=\frac{\partial f}{\partial x}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\eta~\in~(y,y+h_{2})$ tal que
$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}$$
por otro lado

$$\psi'(y)=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right)(x,y)=\frac{\partial^{2}f}{\partial y\partial x}(x,y)$$
por lo tanto
$$\psi'(\eta)=\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)$$
de esta manera

$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}=\left(\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)\right)h_{2}$$
y si $\theta\in (x,x+h_{1})$ tenemos entonces que

$$\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}$$
en consecuencia
$$M=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}$$

Consideremos ahora $$\overline{\varphi}(y)=f(x+h_{1},y)-f(x,y)$$de manera que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$

Aplicando el TVM a $\overline{\varphi}$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\overline{\eta}~\in~(y,y+h_{2})$ tal que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}$$
por otro lado
$$\overline{\varphi}'(y)=\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)$$
por lo tanto

$$\overline{\varphi}'(\overline{\eta})=\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})$$
tenemos entonces que
$$M=\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{2}$$

Consideremos ahora $\displaystyle{\overline{\psi}(x)=\frac{\partial f}{\partial y}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\overline{\theta}~\in~(x,x+h_{1})$ tal que
$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}$$
por otro lado

$$\overline{\psi}'(x)=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right)(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$
por lo tanto
$$\overline{\psi}'(\overline{\theta})=\frac{\partial^{2}f}{\partial y\partial x}(\overline{\theta},y)$$
de esta manera

$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
es decir
$$\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
y si $\overline{\eta}\in (y,y+h_{2})$ tenemos entonces que
$$\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{1}$$
en consecuencia

$$M=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{1}h_{2}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
igualando ambas expresiones de M se tiene
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
donde
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)$$
Tomando limite cuando $h_{1},h_{2}\rightarrow 0$ y usando la continuidad asumida de las parciales mixtas se tiene que $\theta,\overline{\theta}\rightarrow x$ y $\eta,\overline{\eta}\rightarrow y$ se concluye
$$\frac{\partial^{2}f}{\partial y\partial x}(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$ $\square$

Ejemplo. Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$\
En este caso
$$\frac{\partial f}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$
$$\frac{\partial f}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$
$$\frac{\partial^{2} f}{\partial x^{2}}=6x+6y-4y^{2}$$
$$\frac{\partial^{2} f}{\partial y^{2}}=-4x^{2}-12y^{2}$$
$$\frac{\partial^{2} f}{\partial x\partial y}=6x-8xy+3$$
$$\frac{\partial^{2} f}{\partial y\partial x}=6x-8xy+3$$

Ejemplo. Dada la función

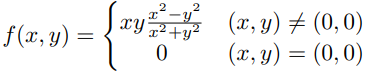
tenemos que para $(x,y)\neq (0,0)$
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
$$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
para el primer caso hacemos $x=0$ y tenemos
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{x=0}-y$$ para el segundo caso hacemos $y=0$ y tenemos $$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{y=0}1$$
Calculamos ahora
$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} (-y)}{\partial y\partial x}=-1$$
$$\frac{\partial^{2} f}{\partial x\partial y}=\frac{\partial^{2} (1)}{\partial x\partial y}=1$$
por lo tanto
$$\frac{\partial^{2} f}{\partial y\partial x}=-1\neq 1=\frac{\partial^{2} f}{\partial x\partial y}$$
En este caso las parciales segundas no son contiuas en $(0,0)$

Teorema. Caso General

Sea $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ definida en el abierto A de $\mathbb{R}^{n}$ tal que
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}$$ sean continuas en A, entonces
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}=\frac{\partial^{2} f}{\partial x_{j}\partial x_{i}}$$