Caso particular de la regla de la cadena

Supongamos que $C:\mathbb{R}\rightarrow\mathbb{R}^{3}$ es una trayectoria diferenciable y $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$.

Sea $h(t)$=$f(x(t), y(t), z(t))$ donde $c(t)$=$(x(t),y(t), z(t))$.
Entonces

$$\displaystyle\frac{\partial{h}}{\partial{t}} = \displaystyle\frac{\partial{f}}{\partial{x}}\cdot \frac{\partial{x}}{\partial{t}}+\frac{\partial{f}}{\partial{y}}\cdot
\frac{\partial{y}}{\partial{t}}+\frac{\partial{f}}{\partial{z}}\cdot
\frac{\partial{z}}{\partial{t}}$$

Esto es:
$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\nabla{f(c(t))}\cdot
{c'(t)}$, ~donde $c'(t)$=$((x'(t), y'(t), z'(t))$

Demostración. Por definición
$\displaystyle\frac{\partial{h}}{\partial{t}}(t_{0})$=$\displaystyle\lim_{t\rightarrow0}\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$
Sumando y restando tenemos que

$\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$=$\displaystyle\frac{f(c(t))-f(c(t_{0}))}{t-t_{0}}$=$\displaystyle\frac{f(x(t), y(t), z(t)) – f(x(t_{0}), y(t_{0}), z(t_{0}))}{t-t_{0}}$=

=$\frac{f(x(t), y(t), z(t))~-~f(x(t_{0}), y(t),
z(t))~+~f(x(t_{0}), y(t), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t))~+~f(x(t_{0}), y(t_{0}), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t_{0}))}{t-t_{0}}$…$\ast$

Aplicando el Teorema del valor medio $\textbf{(T.V.M.)}$

$f(~x(t),~y(t),~z(t))-f(~x(t_{0}),~y(t),~z(t))=\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~(x(t)-x(t_{0}))$

$f(~x(t_{0}),~y(t),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t))=\displaystyle\frac{\partial{f}}{\partial{y}}~(x(t),~ d, ~z(t))~(y(t)-y(t_{0}))$

$f(~x(t_{0}),~y(t_{0}),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t_{0}))=\displaystyle\frac{\partial{f}}{\partial{z}}(~x(t),~y(t),~e)~(z(t)-z(t_{0}))$

$\therefore$$\ast$=$\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~\displaystyle\frac{x(t)-x(t_{0})}{t-t_{0}}+\displaystyle\frac{\partial{f}}{\partial{y}}~(~x(t),~d,~z(t))~\displaystyle\frac{y(t)-y(t_{0})}{t-t_{0}}$+

$+\displaystyle\frac{\partial{f}}{\partial{z}}~(~x(t),~y(t),~e))~\displaystyle\frac{z(t)-z(t_{0})}{t-t_{0}}$

Tomando $\displaystyle\lim_{t\rightarrow{t_{0}}}$ y por la continuidad de las parciales

$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\displaystyle\frac{\partial{f}}{\partial{x}}~\frac{\partial{x}}{\partial{t}}+ \displaystyle\frac{\partial{f}}{\partial{y}}~\frac{\partial{y}}{\partial{t}}+\displaystyle\frac{\partial{f}}{\partial{z}}~\frac{\partial{z}}{\partial{t}}$

Ejemplos: Caso particular de la regla de la cadena

Ejemplo. Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+3y^{2}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$

Solución. En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=2x\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=2e^{t}\cdot e^{t}=2e^{2t}$$

$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (\cos(t))}{dt}=6y\left|{(e^{t},\cos(t))}\cdot (-sen(t))\right.=6 cos(t) \cdot (- sen(t))$$
por lo tanto
$$h'(t)=2e^{2t}-6\cos(t)\cdot (sen(t))$$

Ejemplo. Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=xy$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$

Solución. En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (xy)}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=y\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=\cos(t)\cdot e^{t}$$

$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (xy)}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (cos(t))}{dt}=x\left|{(e^{t},cos(t))}\cdot (-sen(t))\right.=e^{t}\cdot (-sen(t))$$

por lo tanto
$$h'(t)=\cos(t)e^{t}-e^{t}\cdot sen(t)$$

Ejemplo.Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=e^{xy}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(3t^{2},t^{3})$

Solución. En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene

$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial x}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (3t^{2})}{dt}=ye^{xy}\left|{(3t^{2},t^{3})}\cdot 6t\right.=t^{3}e^{3t^{5}}6t=6t^{4}e^{3t^{5}}$$

$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial y}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (t^{3})}{dt}=xe^{xy}\left|{(3t^{2},t^{3})}\cdot 3t^{2}\right.=3t^{2}e^{3t^{5}}3t^{2}=9t^{4}e^{3t^{5}}$$
por lo tanto
$$h'(t)=6t^{4}e^{3t^{5}}+9t^{4}e^{3t^{5}}=15t^{4}e^{3t^{5}}$$

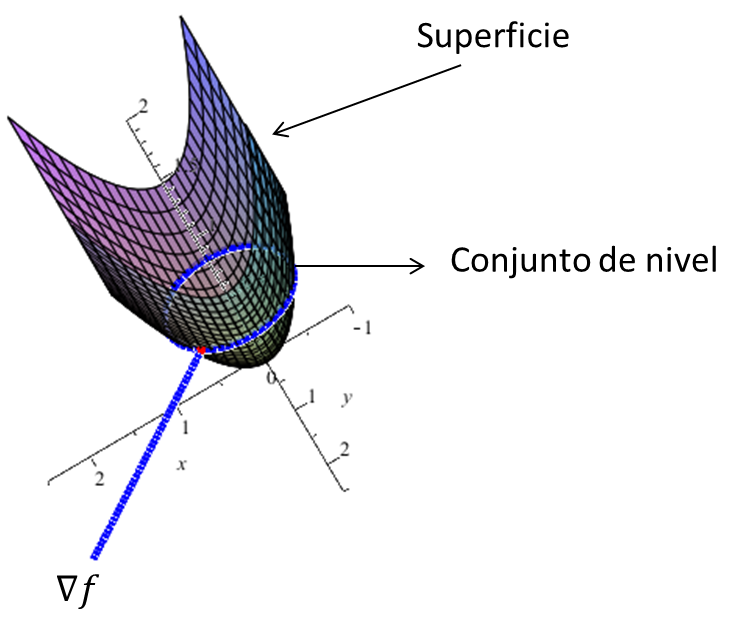
Teorema 1. El gradiente es normal a las superficies de nivel. Sea $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ una aplicación $C^{1}$ y sea
$(x_{0},y_{0},z_{0})$ un punto sobre la superficie de nivel $S$ definida por $f(x,y,z)$=$k$, $k$=$cte$. Entonces $\nabla{f}(x_{0},~y_{0},~z_{0})$ es normal a la superficie de nivel en el siguiente sentido: si $v$ es el vector tangente en $t$=$t_{0}$ de
una trayectoria $c(t)$ con $c(t_{0})$=$(x_{0},~y_{0},~z_{0})$ Entonces $\nabla{f}\cdot {v}$=$0$

que se puede escribir como
$$\left(\frac{\partial f}{\partial x}(x(t),y(t)z(t)),\frac{\partial f}{\partial y}(x(t),y(t)z(t)),\frac{\partial f}{\partial z}(x(t),y(t)z(t))\right)\cdot\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)=0$$
en $t=t_{0}$
$$\nabla f(x(0),y(0),z(0))\cdot c'(t_{0})=0$$

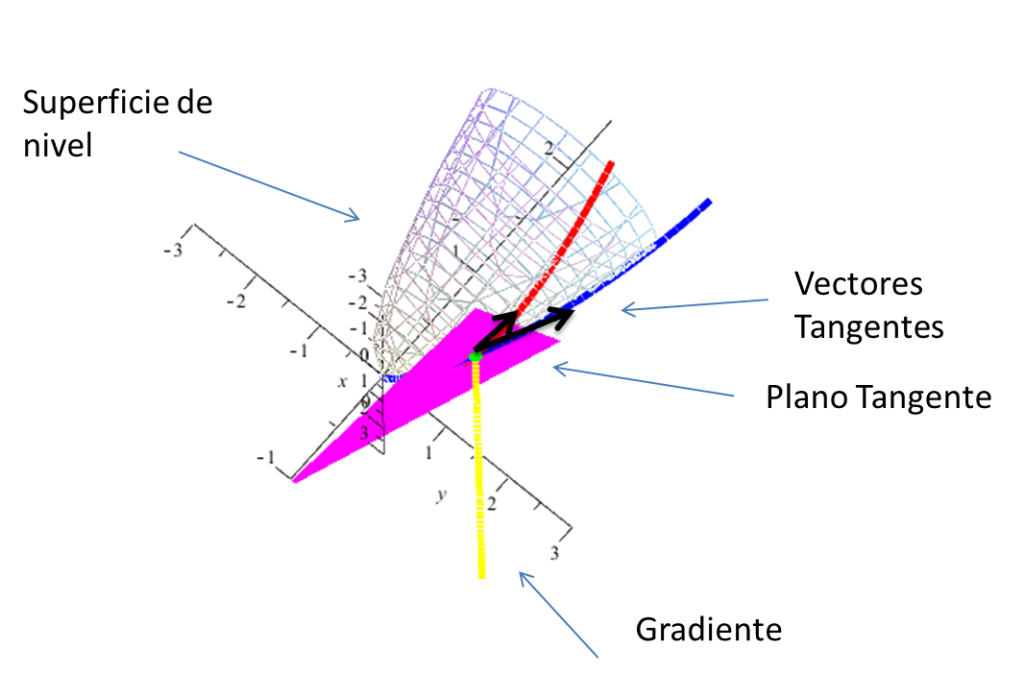
Plano Tangente

Sea $f:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}$ una función diferenciable definida en A, y sea
$$S={(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c}$$

una superficie de nivel de f y $\hat{x}{0}=(x{0},y_{0},z_{0})$ un punto de ella. Considere además, una curva
$$\alpha(t)=(x(t),y(t),z(t))$$
y una curva
$$\beta(t)=(x_{1}(t),y_{1}(t),z_{1}(t))$$

que pasen por $\hat{x}{0}$ con $t\in[a,b]$ en ambos casos y tanto $\alpha$ como $\beta$ diferenciables, se tiene entonces $$(f\circ\alpha)'(t)=f'(\alpha(t))\alpha'(t)=\nabla f(\alpha(t))\cdot \alpha'(t)=0$$ $$(f\circ\beta)'(t)=f'(\beta(t))\beta'(t)=\nabla f(\beta(t))\cdot \beta'(t)=0$$ pues el gradiente $\nabla f(\hat{x}{0})$ en ambos casos es ortogonal tanto al vector $\alpha'(t_{0})$ como al vector $\beta'(t_{0})$ en el punto $\hat{x_{0}}=\alpha(t_{0})=\beta(t_{0})$

Si $\nabla f(\hat{x}{0})\neq 0$, entonces las tangentes a las curvas $\alpha, \beta$ sobre S que pasan por $\hat{x}{0}$

están contenidas en un mismo plano; por lo que el plano tangente a
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c \right\}$$ se define

Definición. El plano tangente a S en $\hat{x}{0}$ se define $$P={\hat{x}~|~\nabla f(\hat{x}{0})\cdot (\hat{x}-\hat{x}_{0})=0}$$

Ejemplo. Hallar el plano tangente a la superficie
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~\frac{x^{2}}{4}-\frac{y^{2}}{9}+z^{2}=1 \right\}$$
en el punto $(2,3,1)$

Solución. En este caso el gradiente es
$$\nabla f(x,y,z)=\left(\frac{x}{2},-\frac{2}{9}y,2z\right)$$
en el punto $(2,3,1)$ es
$$\nabla f(2,3,1)=\left(1,-\frac{2}{3},2\right)$$
Por tanto la ecuación del plano tangente es
$$\left(1,-\frac{2}{3},2\right)\cdot (x-1,y-3,z-1)=0$$
es decir
$$3x-2y+6z-6=0$$