$\textit{MATERIAL EN REVISIÓN}$
Introducción
El contenido de esta sección se basa predominantemente en el libro
Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015, págs 26-30.
Mostraremos resultados formales de la integral de Riemann-Stieltjes. Recordemos que en la entrada anterior partimos de dos funciones acotadas $f:[a,b] \to \mathbb{R}$ y $\alpha:[a,b] \to \mathbb{R}$ y una partición $P=\{x_0 = a,…,x_n =b\}$ en $[a,b]$ con puntos $\xi_i \in [x_{i-1}, x_i].$ Definimos la suma de Riemann-Stieltjes como
$$S(P,f,\alpha) := \sum_{i=1}^{n}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1})).$$
Este resultado depende de $P, \, f$ y $\alpha.$ En esta ocasión, más que hacer $n \to \infty$ haremos que la norma de la partición tienda a cero. Cuando existe $I \in \mathbb{R}$ tal que para cada $\varepsilon >0,$ existe $\delta >0$ tal que si $|P|< \delta$
y para cualquier elección de los puntos $\xi_i$ se cumple que $|I \, – \, S(P,f,\alpha)|< \varepsilon,$ diremos que
$$I := \underset{|P| \to 0}{lim} \, S(P,f,\alpha).$$
Si es finito lo llamamos integral de Riemann-Stieltjes de $f$ con respecto a $\alpha$ en $[a,b].$ El valor de $I \,$ se denota como:
$$\int_{a}^{b}f(x) \, d\alpha := \int_{a}^{b}f \, d\alpha.$$
Por supuesto que este límite no siempre existe en $\mathbb{R}.$ Conozcamos una equivalencia que muestra cuando sí.
Proposición. Criterio de Cauchy para la integral de Riemann-Stieltjes. La integral $\int_{a}^{b}f \, d\alpha$ existe si y solo si para cada $\varepsilon>0$ existe $\delta>0$ tal que si $|P|, \, |Q|< \delta$ entonces
$$|S(P,f,\alpha) \, – \, S(Q,f,\alpha)|< \varepsilon.$$
Demostración:
La ida de la proposición es inmediata por la desigualdad del triángulo: Si la integral $I$ existe entonces para cada $\varepsilon > 0$, existe $\delta > 0$ tal que si $|P|, |Q| < \delta$, de modo que $|S(P,f,\alpha) – I| < \frac{\varepsilon}{2}$ y $|S(Q,f,\alpha) – I| < \frac{\varepsilon}{2}$. Por lo tanto:
$$|S(P,f,\alpha) – S(Q,f,\alpha)| \leq |S(P,f,\alpha) – I| + |I – S(Q,f,\alpha)| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.$$
En el regreso buscamos probar la existencia del límite $I$. Utilizaremos la completitud de los números reales.
Para cada $n \in \mathbb{N}$, sea $\varepsilon_n = \frac{1}{n}$. Por hipótesis, existe $\delta_n > 0$ tal que si $|P|, |Q| < \delta_n$, entonces $|S(P,f,\alpha) – S(Q,f,\alpha)| < \frac{1}{n}$.
Podemos construir una sucesión de particiones $(P_n)_{n \in \mathbb{N}} \,$ como sigue:
Elegimos $P_1 \in \mathcal{P}_{[a,b]}$ tal que $|P_1| < min\{\delta_1, 1\}.$
Elegimos $P_2 \in \mathcal{P}_{[a,b]}$ tal que $|P_2| < min\{\delta_2, \delta_1, \frac{1}{2}\}.$
Elegimos $P_3 \in \mathcal{P}_{[a,b]}$ tal que $|P_3| < min\{\delta_3, \delta_2, \delta_1, \frac{1}{3}\}.$
.
.
.
Elegimos $P_k \in \mathcal{P}_{[a,b]}$ tal que $|P_k| < min\{\delta_k,…\delta_2, \delta_1, \frac{1}{k}\}.$
Nota que la sucesión de números reales $(S(P_n, f, \alpha))_{n \in \mathbb{N}} \,$ es una sucesión de Cauchy, pues dado $\varepsilon > 0$, existe $N \in \mathbb{N}\, $ tal que $\frac{1}{N}< \varepsilon.$
Por otro lado, para $n, m \geq N$ se cumple que $\frac{1}{n}, \frac{1}{m} < \frac{1}{N}$,
en consecuencia, tanto $|P_n|$ como $|P_m|$ son menores que $\frac{1}{N}$ y menores que $\delta_N.$ Se sigue que:
$$|S(P_n,f,\alpha) \, – \, S(P_m,f,\alpha)|< \frac{1}{N} < \varepsilon.$$
Dado que $\mathbb{R}$ es completo, existe $I \in \mathbb{R}$ tal que $\underset{n \to \infty}{lim} S(P_n, f, \alpha) = I$.
Finalmente, veamos que $I$ es efectivamente el límite cuando $|P| \to 0$. Sea $\varepsilon > 0$. Elegimos $k \in \mathbb{N}$ tal que $\frac{1}{k} < \frac{\varepsilon}{2}$ y $|S(P_k, f, \alpha) – I| < \frac{\varepsilon}{2}$. Si tomamos $\delta = \delta_k$, entonces para cualquier partición $P$ con $|P| < \delta$, tenemos:
$$|S(P,f,\alpha) – I| \leq |S(P,f,\alpha) – S(P_k, f, \alpha)| + |S(P_k, f, \alpha) – I| < \frac{1}{k} + \frac{\varepsilon}{2} < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.$$
Por lo tanto, la integral existe y es igual a $I$.
Ejemplos
- Sean $f, \alpha :[a,b] \to \mathbb{R}$ con $f$ continua y $\alpha$ continuamente diferenciable, entonces
$$\int_{a}^{b}f \, d\alpha = \int_{a}^{b}f \, \alpha’ \, dx$$
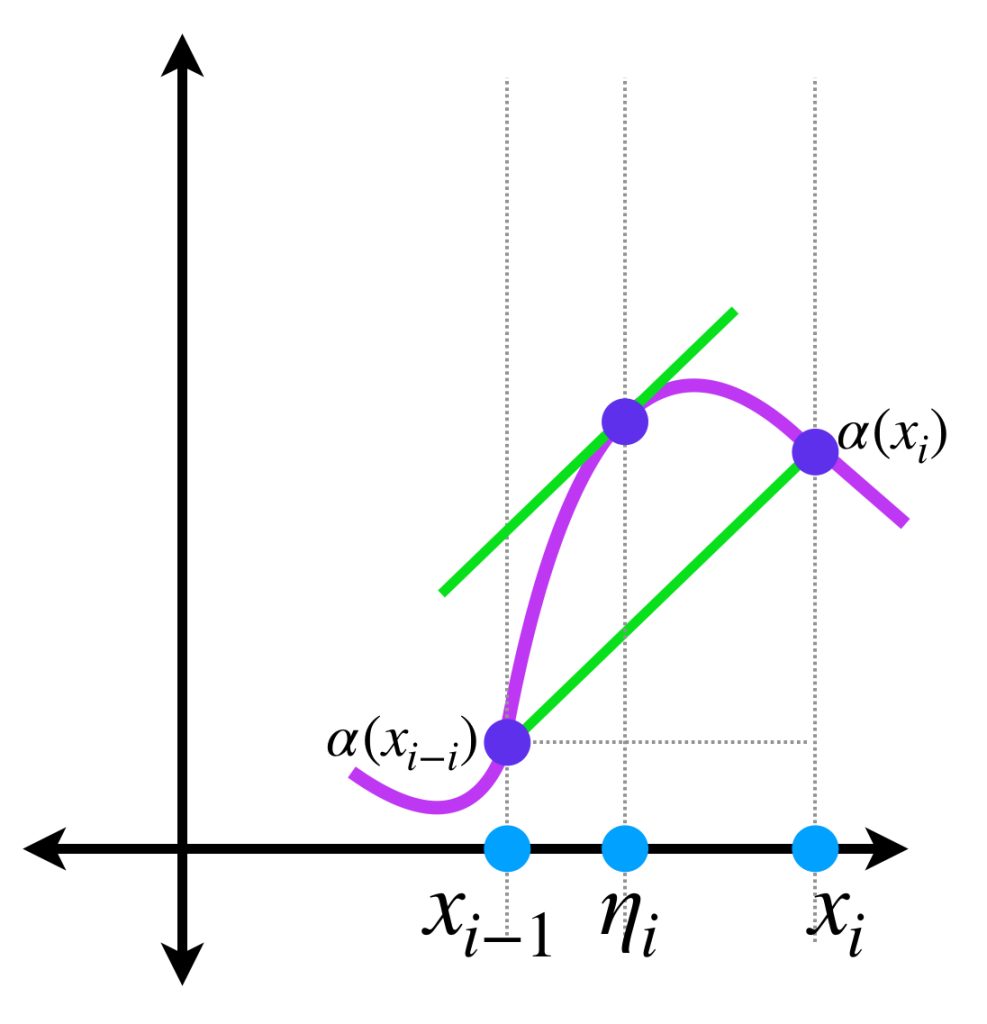
De hecho, por el teorema del valor medio aplicado en $\alpha,$ para cada $i = 1,2,..,n$ existen $\eta_i \in [x_{i-1}, x_i]$ tales que
\begin{align}
S(P,f,\alpha) &= \sum_{i=1}^{n}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1})) \\
&= \sum_{i=1}^{n}f(\xi_i)\alpha'(\eta_i)(x_i \, – \, x_{i-1}).
\end{align}
Usando la continuidad uniforme de $\alpha’$ podemos asumir que, en intervalos muy pequeños, $\alpha'(\eta_i)= \alpha'(\xi_i),$ en consecuencia
$$\sum_{i=1}^{n}f(\xi_i)\alpha'(\eta_i)(x_i \, – \, x_{i-1})= \sum_{i=1}^{n}f(\xi_i)\alpha'(\xi_i)(x_i \, – \, x_{i-1})$$
Nota que esto ya es la común suma de Riemann y así:
$$\underset{|P| \to 0}{lim} \, S(P,f,\alpha)= \int_{a}^{b} f \, \alpha’ \, dx,$$
o bien
$$\int_{a}^{b}f \, d\alpha = \int_{a}^{b}f \, \alpha’ \, dx.$$
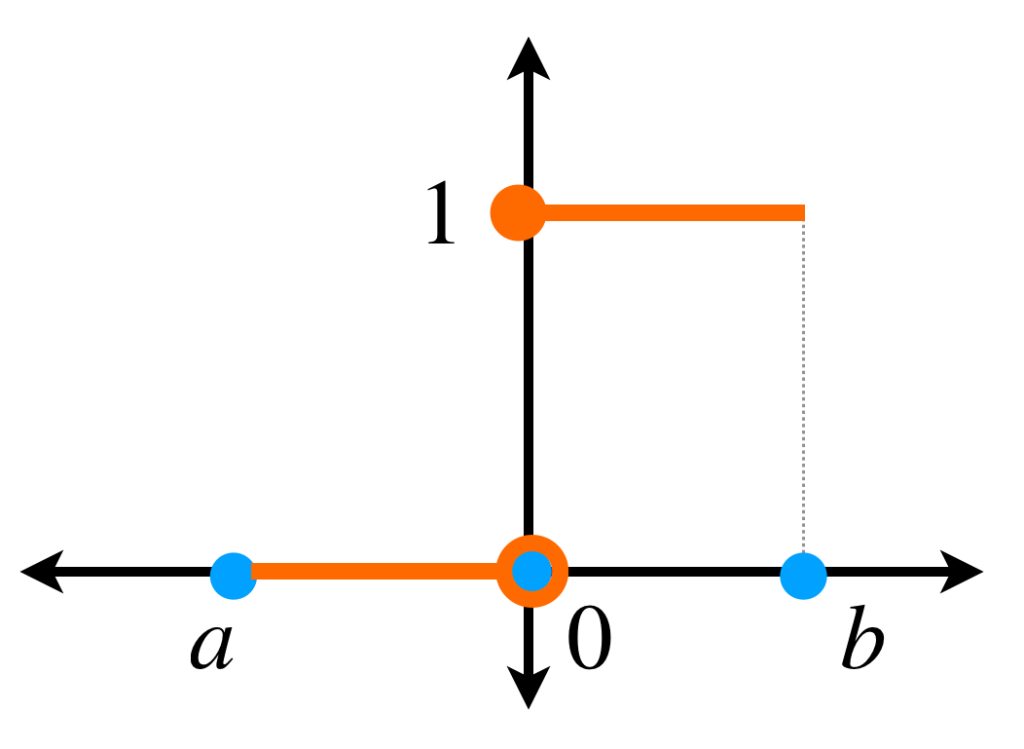
- Ahora considera $f, \alpha: [a,b] \to \mathbb{R}$ donde
\begin{equation*}
\alpha(x) = \begin{cases}
1 \text{ si $x \geq 0$} \\
\\
0 \text{ si $x < 0$}
\end{cases}
\end{equation*}
y $f$ es una función continua en $0.$ Es sencillo demostrar que
$$\int_{-1}^{1}f \, d\alpha = f(0).$$
A continuación enunciaremos algunas propiedades de la integral de Riemann-Stieltjes. Las demostraciones las dejaremos como ejercicio.
Proposición. Sean $f, f_1, f_2, \alpha, \alpha_1$ y $\alpha_2$ funciones de $[a,b] \to \mathbb{R}$ y $c \in \mathbb{R},$ entonces se satisfacen:
a) Si $\int_{a}^{b} f \, d\alpha$ existe, entonces también existen tanto $\int_{a}^{b}cf \, d\alpha$ como $\int_{a}^{b}f \, d(c\alpha)$ y además
$$\int_{a}^{b}cf \, d\alpha = \int_{a}^{b}f \, d(c\alpha) = c \int_{a}^{b}f \, d\alpha.$$
b) Si tanto $\int_{a}^{b} f_1 \, d\alpha$ como $\int_{a}^{b} f_2 \, d\alpha$ existen, entonces también
$\int_{a}^{b} (f_1 + f_2) \, d\alpha$ existe y
$$\int_{a}^{b} (f_1 + f_2) \, d\alpha = \int_{a}^{b} f_1 \, d\alpha + \int_{a}^{b} f_2 \, d\alpha.$$
c) Si tanto $\int_{a}^{b} f \, d\alpha_1$ como $\int_{a}^{b} f \, d\alpha_2$ existen, entonces también
$\int_{a}^{b} f \, d(\alpha_1+ \alpha_2)$ existe y
$$\int_{a}^{b} f \, d(\alpha_1+ \alpha_2) = \int_{a}^{b} f \, d\alpha_1 + \int_{a}^{b} f \, d\alpha_2.$$
Para finalizar esta sección, veremos que es posible obtener la integral de Riemann-Stieltjes como equivalencia de la suma de integrales correspondientes a cada división del intervalo, como muestra la siguiente:
Proposición. Si $\int_{a}^{b} f \, d\alpha$ existe y $a \leq c \leq b,$ entonces
a) Tanto $\int_{a}^{c}f \, d\alpha$ como $\int_{c}^{b}f \, d\alpha$ existen y
b) $\int_{a}^{b}f \, d\alpha = \int_{a}^{c}f \, d\alpha + \int_{c}^{b} f \, d\alpha.$
Demostración:
Para simplificar la notación, hagamos $S_P[a,b] = S(P,f,\alpha)$ donde $P \in \mathcal{P}_{[a,b]}.$
Para mostrar que $\int_{a}^{c} f \, d\alpha$ existe, de acuerdo con el criterio de Cauchy para la integral de Riemann-Stieltjes encunciado arriba, será suficiente probando que para todo $\varepsilon>0$ existe $\delta>0$ tal que si $P_1, \, P_2 \in \mathcal{P}_{[a,c]}$ con $|P_1|, \, |P_2|< \delta,$ entonces
\begin{align}
|S_{P_1}[a,c] \, – \, S_{P_2}[a,c]| < \varepsilon.
\end{align}
Como $\int_{a}^{b}f \, d\alpha \,$ existe entonces dada $\varepsilon>0$ existe $\delta>0$ tal que para cualesquiera $P’_1, \, P’_2 \in \mathcal{P}_{[a,b]}$ con $|P’_1|, \, |P’_2|< \delta, \,$ tenemos
\begin{align}
|S_{P’_1}[a,b] \, – \, S_{P’_2}[a,b]| < \varepsilon.
\end{align}
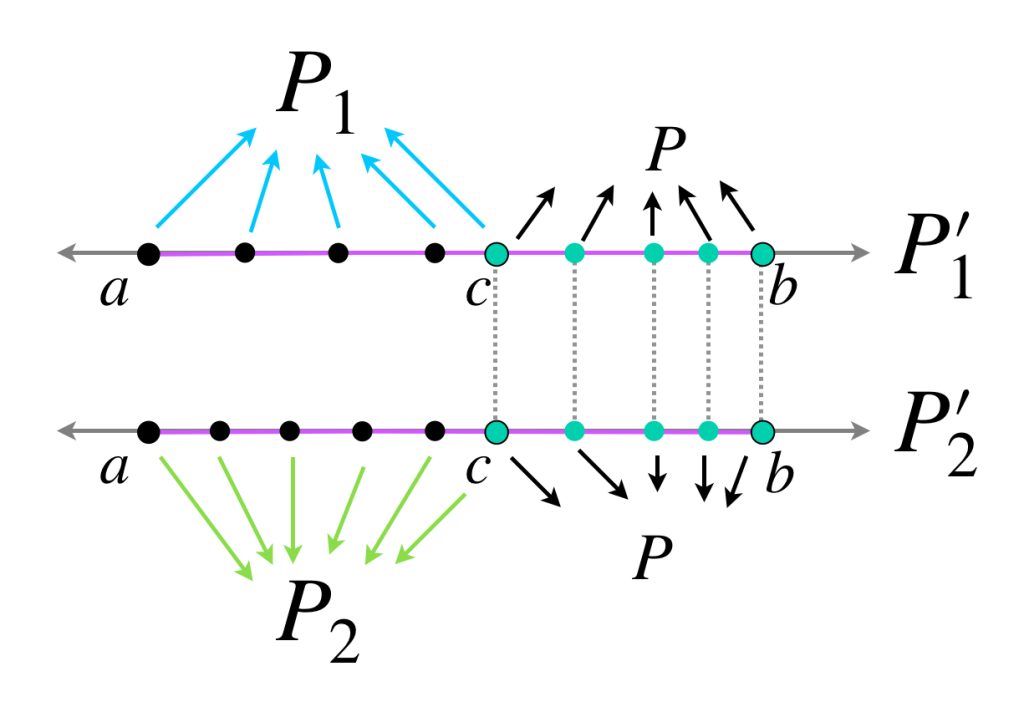
Sean $P_1, \, P_2 \in \mathcal{P}_{[a,c]}$ tales que $|P_1|, \, |P_2|< \delta$ y toma $P \in \mathcal{P}_{[c,b]}$ tal que también $|P|< \delta.$
Definimos $P’_1 = P_1 \cup P \, $ y $\, P’_2 = P_2 \cup P.$ Nota que ambas son particiones de $[a,b]$ cuya norma es menor que $\delta$ y por tanto satisfacen (4).
Notemos que
\begin{align}
S_{P’_1}[a,b] &= S_{P_1}[a,c]+ S_{P}[c,b] \\
\text{y } S_{P’_2}[a,b] &= S_{P_2}[a,c]+ S_{P}[c,b]
\end{align}
así, restando (6) de (5)
\begin{align}
|S_{P_1}[a,c] \, – \, S_{P_2}[a,c] + \cancel{S_{P}[c,b] \, – \, S_{P}[c,b]}| = |S_{P’_1}[a,b] \, – \, S_{P’_2}[a,b]|
\end{align}
De (7) y (4) se cumple (3), por lo tanto
$\int_{a}^{c}f \, d\alpha$ existe.
Análogamente se puede probar que $\int_{c}^{b}f \, d\alpha$ existe, mientras que (5) y (6) permiten concluir que
$$\int_{a}^{b}f \, d\alpha = \int_{a}^{c}f \, d\alpha + \int_{c}^{b}f \, d\alpha$$
que es lo que queríamos demostrar.
Más adelante…
Veremos algunas propiedades más de la integral de Riemann-Stieltjes, por lo pronto desarrolla las ideas con los siguientes ejercicios.
Tarea moral
- Considera $f, \alpha: [a,b] \to \mathbb{R}$ donde
\begin{equation*}
\alpha(x) = \begin{cases}
1 \text{ si $x \geq 0$} \\
0 \text{ si $x < 0$}
\end{cases}
\end{equation*}
y $f$ es una función continua en $0.$ Prueba que
$$\int_{-1}^{1}f \, d\alpha = f(0).$$ - Sean $f, f_1, f_2, \alpha, \alpha_1$ y $\alpha_2$ funciones de $[a,b] \to \mathbb{R}$ y $c \in \mathbb{R}. \,$ Demuestra que se satisfacen:
a) Si $\int_{a}^{b} f \, d\alpha$ existe, entonces también existen tanto $\int_{a}^{b}cf \, d\alpha$ como $\int_{a}^{b}f \, d(c\alpha)$ y además
$$\int_{a}^{b}cf \, d\alpha = \int_{a}^{b}f \, d(c\alpha) = c \int_{a}^{b}f \, d\alpha.$$
b) Si tanto $\int_{a}^{b} f_1 \, d\alpha$ como $\int_{a}^{b} f_2 \, d\alpha$ existen, entonces también
$\int_{a}^{b} (f_1 + f_2) \, d\alpha$ existe y
$$\int_{a}^{b} (f_1 + f_2) \, d\alpha = \int_{a}^{b} f_1 \, d\alpha + \int_{a}^{b} f_2 \, d\alpha.$$
c) Si tanto $\int_{a}^{b} f \, d\alpha_1$ como $\int_{a}^{b} f \, d\alpha_2$ existe, entonces también
$\int_{a}^{b} f \, d(\alpha_1+ \alpha_2)$ existe y
$$\int_{a}^{b} f \, d(\alpha_1+ \alpha_2) = \int_{a}^{b} f \, d\alpha_1 + \int_{a}^{b} f \, d\alpha_2.$$ - Sean $f, \alpha:[a,b] \to \mathbb{R}$ funciones acotadas. Demuestra que si $[a’,b’] \subset [a,b]$ y $\int_{a}^{b} f \, d\alpha$ existe entonces también $\int_{a’}^{b’} f \, d\alpha$ existe.
Bibliografía
- Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015. Págs: 26-30.